2022-2023学年六年级数学下册同步精品课堂(沪教版)5.2 数轴 教学课件(共17张PPT)
文档属性
| 名称 | 2022-2023学年六年级数学下册同步精品课堂(沪教版)5.2 数轴 教学课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
2022-2023学年六年级数学下册同步精品课堂(沪教版)
第 5章 有理数
5.2 数轴
知识回顾
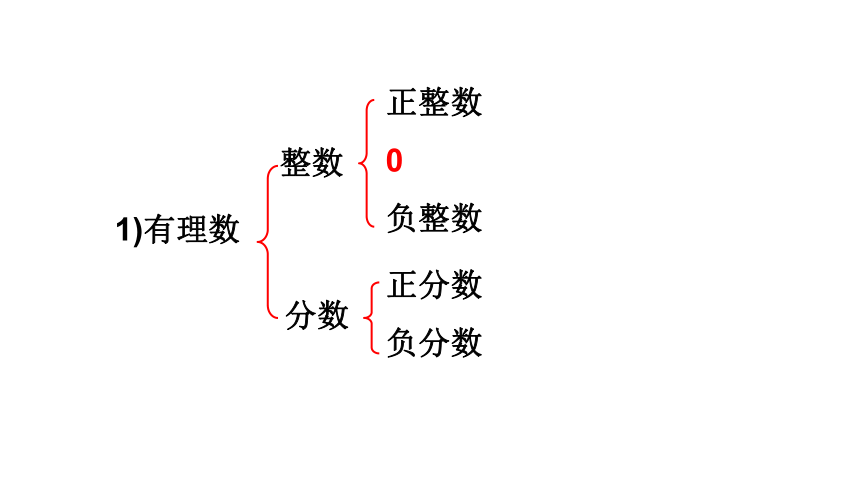
1、什么叫有理数?
整数和分数统称为有理数.
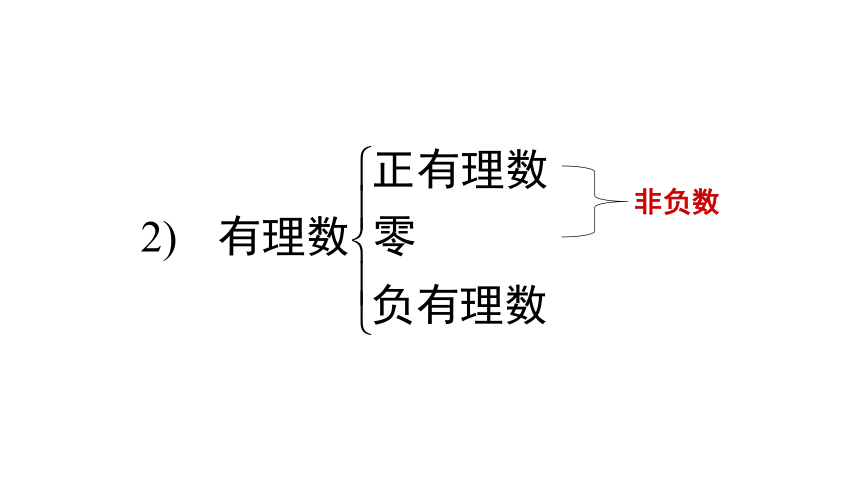
2、有理数可以如何分类?
正整数
0
负整数
正分数
负分数
整数
分数
1)有理数
非负数
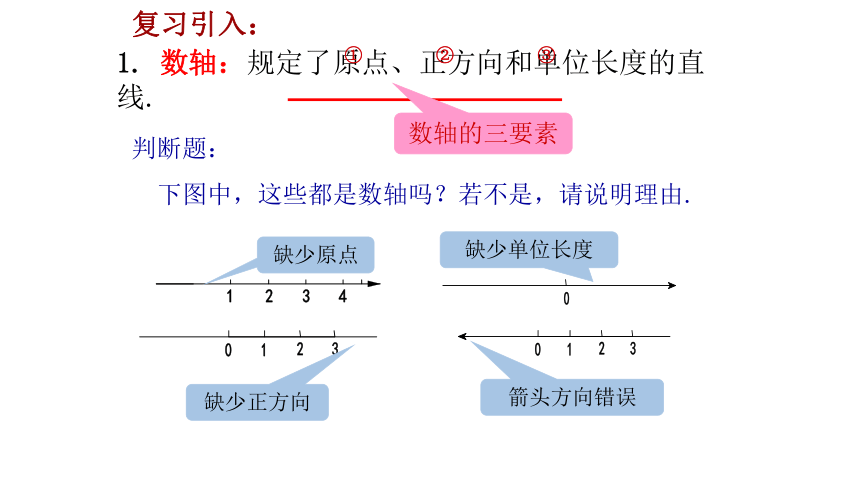
复习引入:
1. 数轴:规定了原点、正方向和单位长度的直线.
判断题:
下图中,这些都是数轴吗?若不是,请说明理由.
缺少原点
箭头方向错误
缺少正方向
缺少单位长度
数轴的三要素
①
②
③
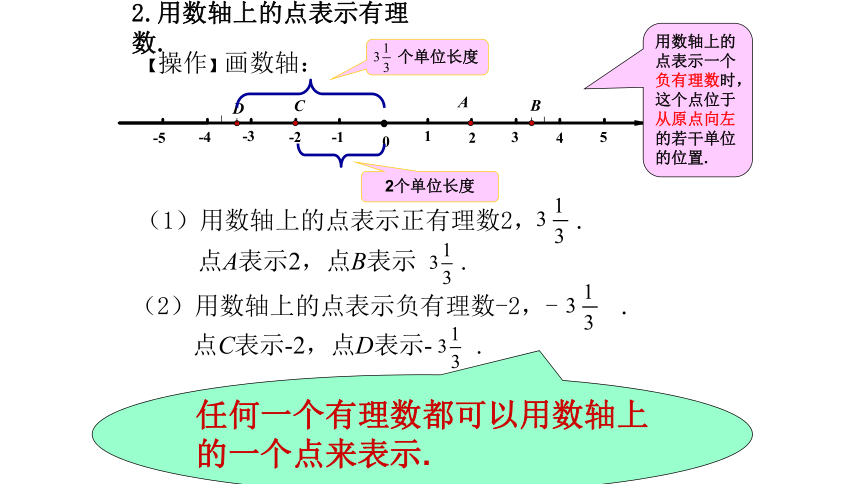
2.用数轴上的点表示有理数.
【操作】画数轴:
(1)用数轴上的点表示正有理数2, .
点A表示2,点B表示 .
(2)用数轴上的点表示负有理数-2,- .
点C表示-2,点D表示- .
个单位长度
2个单位长度
任何一个有理数都可以用数轴上的一个点来表示.
用数轴上的点表示一个负有理数时,这个点位于从原点向左的若干单位的位置.
A
B
C
D
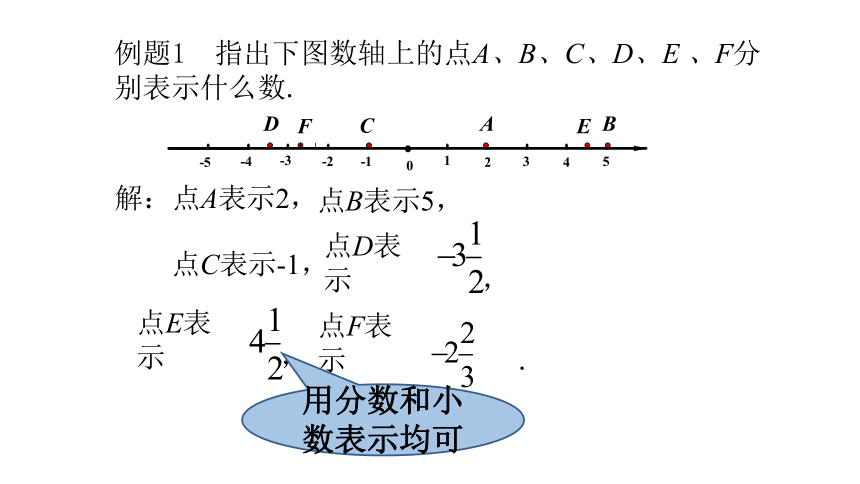
例题1 指出下图数轴上的点A、B、C、D、E 、F分
别表示什么数.
点E表示 ,
点D表示 ,
点F表示 .
解:点A表示2,
点B表示5,
点C表示-1,
A
F
E
C
B
D
用分数和小数表示均可
相反数的意义:
观察:
(1) 3与-3,
(2) 4与-4,
(3) 与 .
只有符号不同,数值完全相同.
只有符号不同的两个数,我们称其中一个为另一个的相反数.也称这两个数互为相反数.
相反数:
零的相反数为零.
例题2 用数轴上的点分别表示-3,4与 和它们的相反数.
解:-3的相反数是3;
4的相反数是-4;
的相反数是 ;
几何意义:在数轴上,表示互为相反数的两个点位于原点的两侧,并且与原点的距离相等.
A
C
B
A’
B’
C’
注:互为相反数的两个数和为0
课本练习
随堂检测
1、下列四个命题:
①符号不同的两个数是相反数;
②3.25是 的相反数;
③互为相反数的两个数一定不等;
④任何一个正数的相反数都是负数.
其中正确的命题的个数有( )个。
A、1 B、2 C、3 D、4
2、下列说法正确的是( )
A.任何一个数的相反数都与这个数本身不同
B.除零以外的数都有它的相反数,零没有相反数
C.数轴上原点两旁的两个点所表示的数互为相反数
D.任何一个数都有相反数
D
3.以下叙述中,正确的是( )
A、正数与负数互为相反数
B、表示相反意义的量的两个数互为相反数
C、任何有理数都有相反数
D、一个数的相反数是负数
C
补充题:
1、一个数的相反数是它本身,这个数是______;
2、一个数的倒数是它本身,这个数是_______;
3、x-3的相反数是3,则x=________;
﹡4、a是最小的自然数,b是最小的正整数,
c和d互为相反数,e是3的倒数,a+b+c+d+e=___.
0
1或-1
0
a=0
b= 1
c+d=0
e=
课堂小结:
任何一个有理数都能用数轴上的一个点表示.
用数轴上的点表示一个负有理数时,这个点位于从原点向左的若干单位的位置.
2. 任何有理数都有相反数; 零的相反数是零.
(2)几何意义:在数轴上,表示互为相反数的两个点位于原点的两侧,并且与原点的距离相等.
(1)表示方法:a的相反数表示为-a;
一个数的相反数的相反数是它本身.
一个数a的相反数记作“-a”
2022-2023学年六年级数学下册同步精品课堂(沪教版)
第 5章 有理数
5.2 数轴
知识回顾
1、什么叫有理数?
整数和分数统称为有理数.
2、有理数可以如何分类?
正整数
0
负整数
正分数
负分数
整数
分数
1)有理数
非负数
复习引入:
1. 数轴:规定了原点、正方向和单位长度的直线.
判断题:
下图中,这些都是数轴吗?若不是,请说明理由.
缺少原点
箭头方向错误
缺少正方向
缺少单位长度
数轴的三要素
①
②
③
2.用数轴上的点表示有理数.
【操作】画数轴:
(1)用数轴上的点表示正有理数2, .
点A表示2,点B表示 .
(2)用数轴上的点表示负有理数-2,- .
点C表示-2,点D表示- .
个单位长度
2个单位长度
任何一个有理数都可以用数轴上的一个点来表示.
用数轴上的点表示一个负有理数时,这个点位于从原点向左的若干单位的位置.
A
B
C
D
例题1 指出下图数轴上的点A、B、C、D、E 、F分
别表示什么数.
点E表示 ,
点D表示 ,
点F表示 .
解:点A表示2,
点B表示5,
点C表示-1,
A
F
E
C
B
D
用分数和小数表示均可
相反数的意义:
观察:
(1) 3与-3,
(2) 4与-4,
(3) 与 .
只有符号不同,数值完全相同.
只有符号不同的两个数,我们称其中一个为另一个的相反数.也称这两个数互为相反数.
相反数:
零的相反数为零.
例题2 用数轴上的点分别表示-3,4与 和它们的相反数.
解:-3的相反数是3;
4的相反数是-4;
的相反数是 ;
几何意义:在数轴上,表示互为相反数的两个点位于原点的两侧,并且与原点的距离相等.
A
C
B
A’
B’
C’
注:互为相反数的两个数和为0
课本练习
随堂检测
1、下列四个命题:
①符号不同的两个数是相反数;
②3.25是 的相反数;
③互为相反数的两个数一定不等;
④任何一个正数的相反数都是负数.
其中正确的命题的个数有( )个。
A、1 B、2 C、3 D、4
2、下列说法正确的是( )
A.任何一个数的相反数都与这个数本身不同
B.除零以外的数都有它的相反数,零没有相反数
C.数轴上原点两旁的两个点所表示的数互为相反数
D.任何一个数都有相反数
D
3.以下叙述中,正确的是( )
A、正数与负数互为相反数
B、表示相反意义的量的两个数互为相反数
C、任何有理数都有相反数
D、一个数的相反数是负数
C
补充题:
1、一个数的相反数是它本身,这个数是______;
2、一个数的倒数是它本身,这个数是_______;
3、x-3的相反数是3,则x=________;
﹡4、a是最小的自然数,b是最小的正整数,
c和d互为相反数,e是3的倒数,a+b+c+d+e=___.
0
1或-1
0
a=0
b= 1
c+d=0
e=
课堂小结:
任何一个有理数都能用数轴上的一个点表示.
用数轴上的点表示一个负有理数时,这个点位于从原点向左的若干单位的位置.
2. 任何有理数都有相反数; 零的相反数是零.
(2)几何意义:在数轴上,表示互为相反数的两个点位于原点的两侧,并且与原点的距离相等.
(1)表示方法:a的相反数表示为-a;
一个数的相反数的相反数是它本身.
一个数a的相反数记作“-a”
