苏科版九年级下册6.6 图形的位似 课件(共15张PPT)
文档属性
| 名称 | 苏科版九年级下册6.6 图形的位似 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 344.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:59:27 | ||
图片预览



文档简介
(共15张PPT)
6.6 图形的位似
关注生活
在玻璃片上画一个三角形,使玻璃片与墙面平行,用点光源把三角形投影到墙面上。你发现了什么?
保持玻璃片与墙面平行,将玻璃片前后移动(玻璃片与点光源间的距离不变),你又能发现什么?
6.6 图形的位似
尝试与交流
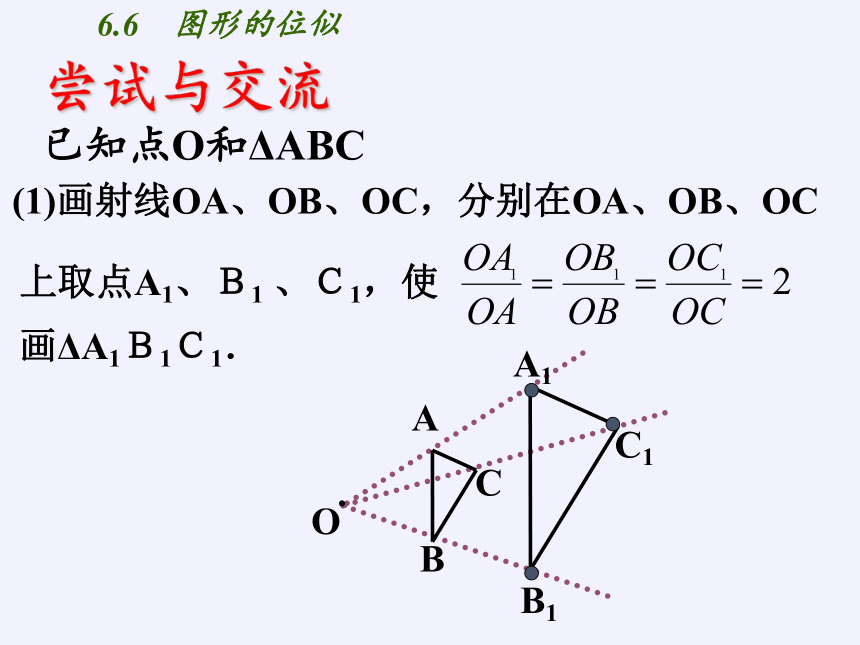
已知点O和ΔABC
(1)画射线OA、OB、OC,分别在OA、OB、OC
画ΔA1B1C1.
上取点A1、B1 、C1,使
A
B
C
A1
B1
C1
O
.
6.6 图形的位似
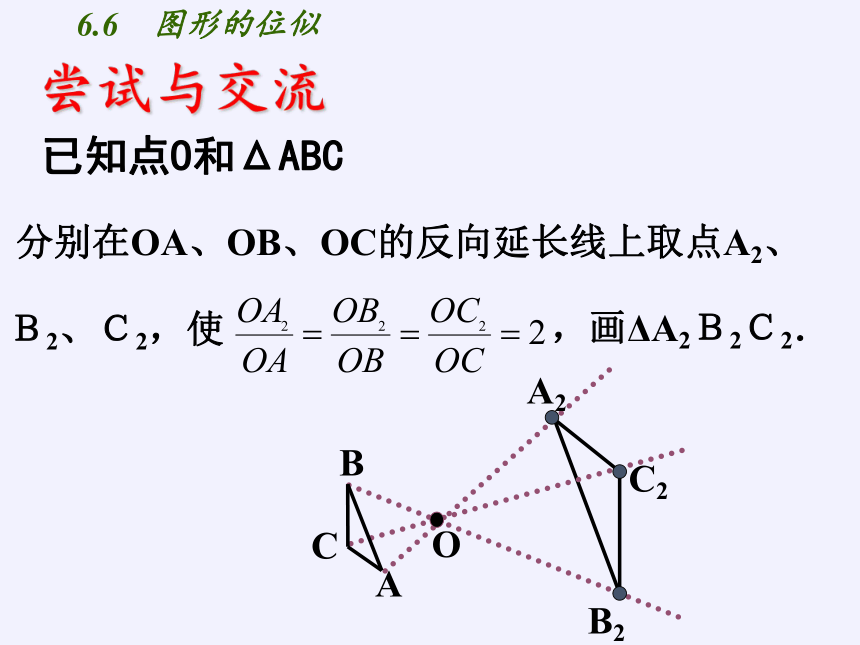
已知点O和ΔABC
分别在OA、OB、OC的反向延长线上取点A2、
B2、C2,使
,画ΔA2B2C2.
O
A
B
C
A2
B2
C2
尝试与交流
6.6 图形的位似
尝试与交流
6.6 图形的位似
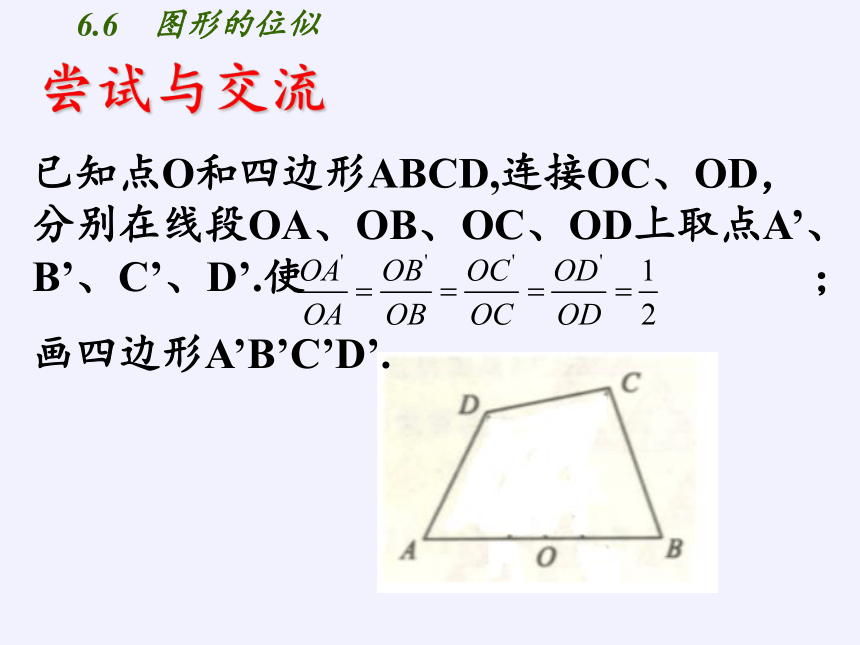
已知点O和四边形ABCD,连接OC、OD,分别在线段OA、OB、OC、OD上取点A’、B’、C’、D’.使 ;
画四边形A’B’C’D’.
A
B
C
A1
B1
C1
O
.
O
A
B
C
A2
B2
C2
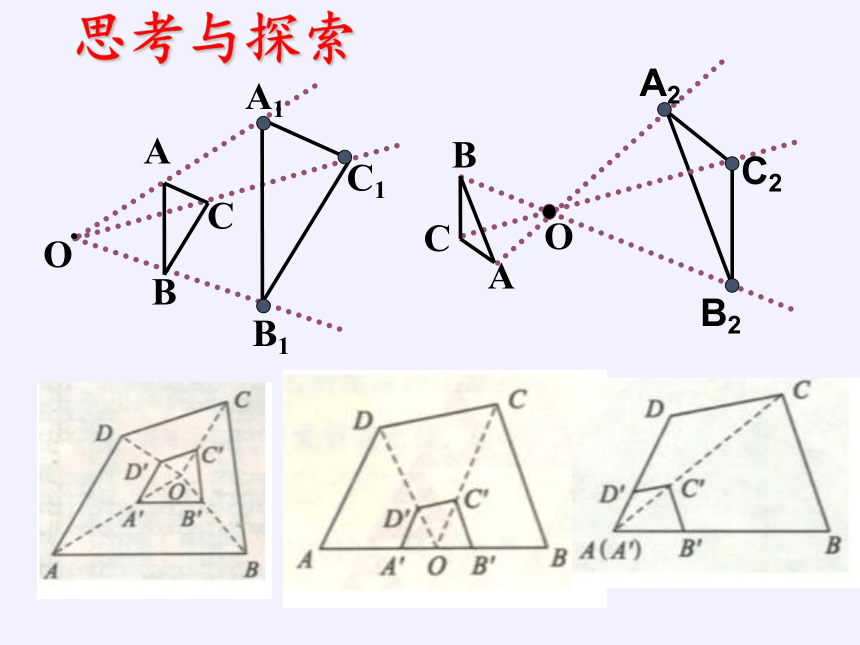
思考与探索
位似形定义:
如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似形.
这个点叫做位似中心.
利用位似可以按所给相似比把一个图形放大或缩小.
图形的位似
6.6 图形的位似
(1)两个位似形一定是相似形;
(2)对应顶点所在的直线都经过同一点;
(3)对应边互相平行(或在同一直线上);
(4)任意一组对应点到位似中心的距离之比等于
相似比.
位似的性质
6.6 图形的位似
y
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
B'
A'
x
B
A
o
观察对应点之间的坐标的变化,你有什么发现
探索:
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A〞
B〞
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
探索:
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(5,4)、B(3,0),分别将点A,B的横坐标、纵坐标都乘2.得到相应的点A'B'坐标.
(1)画△OA'B'.
(2)△OA'B'与△OAB是位似形吗?
为什么?
例题评析
6.6 图形的位似
1.判断:
①位似图形一定是相似图形.( )
②相似图形一定是位似图形.( )
③位似图形中每组对应顶点所在直线相交于一点.( )
④位似图形中每组对应边所在直线必相互平行或在同一直线上.( )
⑤位似图形上对应顶点到位似中心的距离之比等于相似比.( )
随堂练习
6.6 图形的位似
位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。
注意
6.6 图形的位似
通过这节课的学习,你有哪些收获?
课堂小结
6.6 图形的位似
谢 谢
6.6 图形的位似
关注生活
在玻璃片上画一个三角形,使玻璃片与墙面平行,用点光源把三角形投影到墙面上。你发现了什么?
保持玻璃片与墙面平行,将玻璃片前后移动(玻璃片与点光源间的距离不变),你又能发现什么?
6.6 图形的位似
尝试与交流
已知点O和ΔABC
(1)画射线OA、OB、OC,分别在OA、OB、OC
画ΔA1B1C1.
上取点A1、B1 、C1,使
A
B
C
A1
B1
C1
O
.
6.6 图形的位似
已知点O和ΔABC
分别在OA、OB、OC的反向延长线上取点A2、
B2、C2,使
,画ΔA2B2C2.
O
A
B
C
A2
B2
C2
尝试与交流
6.6 图形的位似
尝试与交流
6.6 图形的位似
已知点O和四边形ABCD,连接OC、OD,分别在线段OA、OB、OC、OD上取点A’、B’、C’、D’.使 ;
画四边形A’B’C’D’.
A
B
C
A1
B1
C1
O
.
O
A
B
C
A2
B2
C2
思考与探索
位似形定义:
如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似形.
这个点叫做位似中心.
利用位似可以按所给相似比把一个图形放大或缩小.
图形的位似
6.6 图形的位似
(1)两个位似形一定是相似形;
(2)对应顶点所在的直线都经过同一点;
(3)对应边互相平行(或在同一直线上);
(4)任意一组对应点到位似中心的距离之比等于
相似比.
位似的性质
6.6 图形的位似
y
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
B'
A'
x
B
A
o
观察对应点之间的坐标的变化,你有什么发现
探索:
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A〞
B〞
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
探索:
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(5,4)、B(3,0),分别将点A,B的横坐标、纵坐标都乘2.得到相应的点A'B'坐标.
(1)画△OA'B'.
(2)△OA'B'与△OAB是位似形吗?
为什么?
例题评析
6.6 图形的位似
1.判断:
①位似图形一定是相似图形.( )
②相似图形一定是位似图形.( )
③位似图形中每组对应顶点所在直线相交于一点.( )
④位似图形中每组对应边所在直线必相互平行或在同一直线上.( )
⑤位似图形上对应顶点到位似中心的距离之比等于相似比.( )
随堂练习
6.6 图形的位似
位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。
注意
6.6 图形的位似
通过这节课的学习,你有哪些收获?
课堂小结
6.6 图形的位似
谢 谢
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
