【班海精品】北师大版(新)九年级下-1.5三角函数的应用 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-1.5三角函数的应用 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览







文档简介
(共39张PPT)
5 三角函数的应用
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
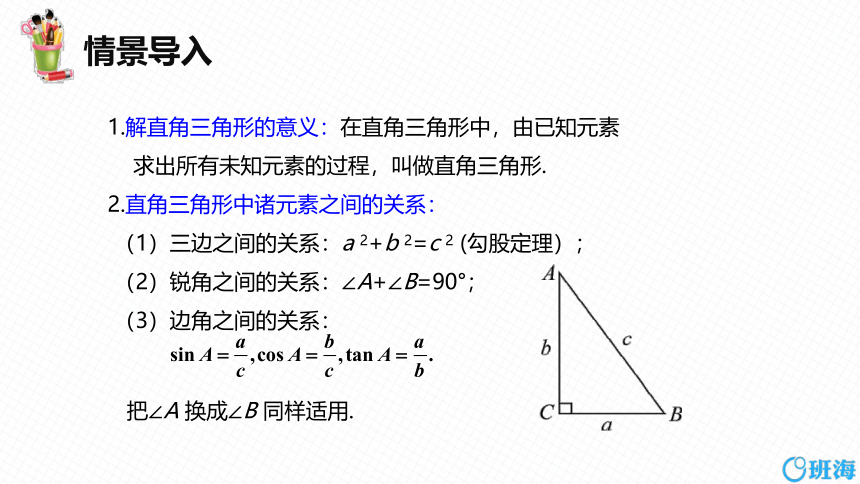
1.解直角三角形的意义:在直角三角形中,由已知元素
求出所有未知元素的过程,叫做直角三角形.
2.直角三角形中诸元素之间的关系:
(1)三边之间的关系:a 2+b 2=c 2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
把∠A 换成∠B 同样适用.
新课精讲
探索新知
1
知识点
借助工具测量的应用
想一想
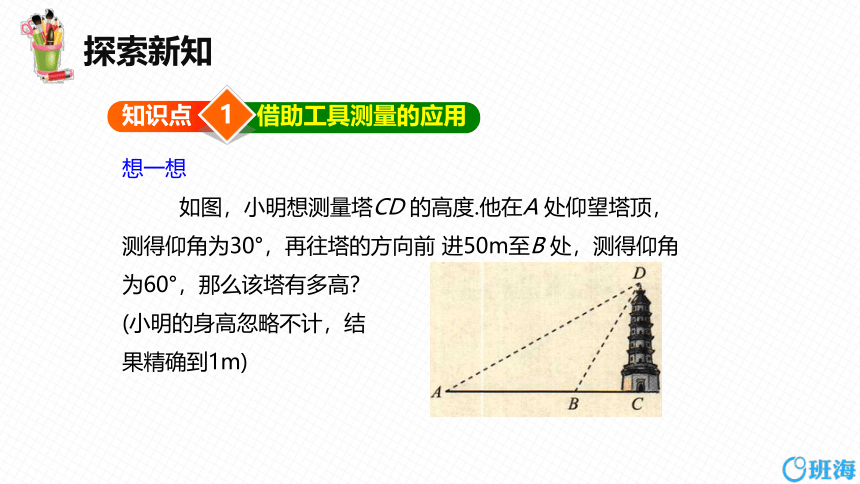
如图,小明想测量塔CD 的高度.他在A 处仰望塔顶,
测得仰角为30°,再往塔的方向前 进50m至B 处,测得仰角
为60°,那么该塔有多高?
(小明的身高忽略不计,结
果精确到1m)
探索新知
1.运用锐角三角函数解决实际问题的方法:
(1)弄清题意,画出示意图;
(2)找出图形中的线段、角所表示的实际意义,并找到所要解决的问题;
(3)寻找要求解的直角三角形,有时需要作适当的辅助线;
(4)选择合适的边角关系式,进行有关锐角三角函数的计算;
(5)按照题目要求的精确度确定答案,并注明单位,作答.
探索新知
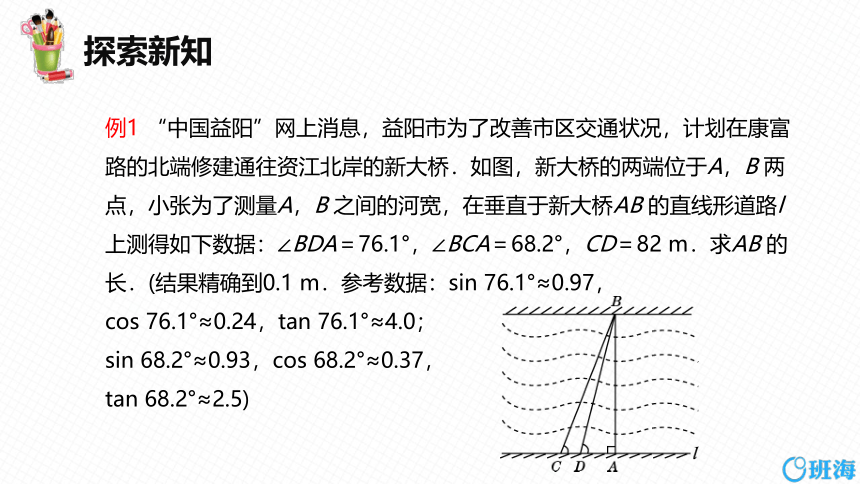
例1 “中国益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥.如图,新大桥的两端位于A,B 两点,小张为了测量A,B 之间的河宽,在垂直于新大桥AB 的直线形道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82 m.求AB 的长.(结果精确到0.1 m.参考数据:sin 76.1°≈0.97,
cos 76.1°≈0.24,tan 76.1°≈4.0;
sin 68.2°≈0.93,cos 68.2°≈0.37,
tan 68.2°≈2.5)
探索新知
设AD=x m,在Rt△ABC 中,利用∠BCA 的正切值,可以用含x 的代数式表示AB. 同理在Rt△ABD 中,利用∠BDA 的正切值表示出AB,从而列出关于x 的方程,求出x 的值就能求出AB 的长了.
导引:
探索新知
设AD=x m,则AC=(x+82) m.
在Rt△ABC 中,tan ∠BCA=
∴AB=AC · tan ∠BCA=(x+82)tan 68.2° m.
在Rt△ABD 中,tan ∠BDA=
∴AB=AD · tan ∠BDA=x tan 76.1° m.
∴(x+82)tan 68.2°=x tan 76.1°. ∴x≈136.67.
∴AB≈4×136.67≈546.7(m).
即AB 的长约为546.7 m.
解:
典题精讲
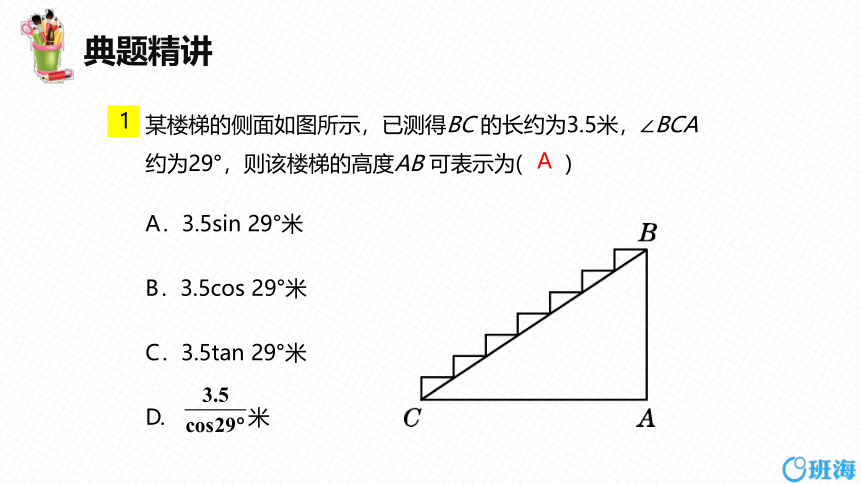
某楼梯的侧面如图所示,已测得BC 的长约为3.5米,∠BCA 约为29°,则该楼梯的高度AB 可表示为( )
A.3.5sin 29°米
B.3.5cos 29°米
C.3.5tan 29°米
D. 米
1
A
典题精讲
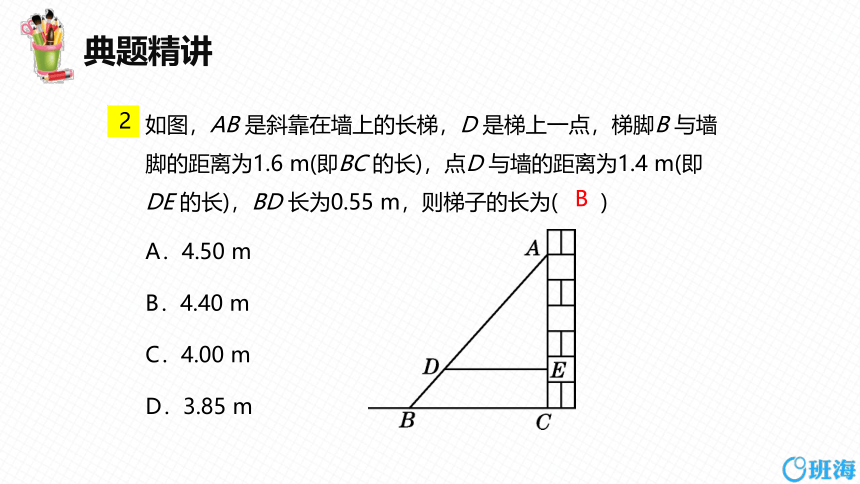
如图,AB 是斜靠在墙上的长梯,D 是梯上一点,梯脚B 与墙脚的距离为1.6 m(即BC 的长),点D 与墙的距离为1.4 m(即DE 的长),BD 长为0.55 m,则梯子的长为( )
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
2
B
典题精讲
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA 的高度与拉绳PB 的长度相等.小明将PB 拉到PB ′的位置,测得∠PB′C=α (B′C 为水平线),测角仪B′D 的高度为1 m,则旗杆PA 的高度为( )
B.
C. D.
3
A
探索新知
2
知识点
借助影子测量的应用
例2 如图,一幢楼房AB 背后有一台阶CD,台阶每层高0.2 m,且
AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°
时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在
台阶的MN 这层上晒太阳( 取1.73).
(1)求楼房的高度约为多少米.
(2)过了一会儿,当α=45°时,
问小猫还能否晒到太阳?
请说明理由.
探索新知
(1)当α=60°时,在Rt△ABE 中,
∵tan 60°=
∴AB=10·tan 60°=10 ≈10×1.73=17.3(m).
即楼房的高度约为17.3 m.
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:假设没有台阶,当α=45°时,从点B 射下的光线与地面AD 的交点为点F,与射线CM 的交点为点H (如下图).
解:
探索新知
∵∠BFA=45°,
∴tan 45°= =1,此时的影长AF=AB≈17.3m.
∴CF=AF-AC≈17.3-17.2=0.1(m).∴CH=CF≈0.1 m.
∴大楼的影子落在台阶MC 这个侧面上,
∴小猫仍可以晒到太阳.
典题精讲
如图,AB 是伸缩式遮阳棚,CD 是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB 的长是________米.(假设夏至的正午时刻阳光与地平面的夹角为60°)
典题精讲
如图,已知电线杆AB 直立于地面上,它的影子恰好
照在土坡的坡面CD 和地面BC 上,如果CD 与地面成
45°,∠A=60°,CD=4 m,BC=(4 -2 ) m,
则电线杆AB 的长为________.
易错提醒
如图,某海岛上的观察所A 发现海上某船只B,并测得其俯角α= 8°35′ .已知观察所 A 的标高(当水位为 0 m时的高度) 为45.54 m,当时水位为+2.34 m.求观察所A 与船只B 的水平距离(结果保留整数,参考数据:sin8°35′≈0.149,cos 8°35′≈0.989,tan 8°35′≈0.151).
易错点:忽略求正切值的前提.
易错提醒
由题意可知AC=45.54-2.34=43.2(m).
在Rt△ABC 中,∠ABC=α=8°35′,
tan ∠ABC=
∴BC=
因此观察所A 与船只B 的水平距离约为286 m.
易错总结:解题时容易弄错AC 的高度,A 处的标高为45.54 m(水位为0 m时的高度),当水位为+2.34 m时,即水位上升了2.34 m,则AC 的高度为45.54-2.34=43.2(m).
解:
学以致用
小试牛刀
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD (D 为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
1
C
小试牛刀
如图,要在宽为22 m的九州大道两边安装路灯,路灯的灯臂CD 长2 m,且与灯柱BC 成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO 与灯臂CD 垂直,当灯罩的轴线DO 通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC 高度应该设计为( )
A.(11-2 ) m
B.(11 -2 ) m
C.(11-2 ) m
D.(11 -4) m
2
D
小试牛刀
3 如图①②分别是某款篮球架的实物图与示意图,已知底座BC=0.60 m,底座BC 与支架AC 所成的角∠ACB=75°,支架AF 的长为2.50 m,篮板顶端F 点到篮框D 的距离FD=1.35 m,篮板底部支架HE 与支架AF 所成的角∠FHE=60°,求篮框D 到地面的距离(结果精确到0.01 m,参考数据:cos 75°≈0.258 8,sin 75°≈0.965 9,tan 75°≈3.732,3≈1.732,2≈1.414)
小试牛刀
如图,延长FE 交CB 于点M,过点A 作AG⊥FM 于点G.
在Rt△ABC 中,tan∠ACB=
∴AB=BC tan 75°≈0.60×3.732≈2.239(m).
∴GM=AB≈2.239 m.
在Rt△AGF 中,∵∠FAG=∠FHE=60°,
sin∠FAG= 即sin 60°=
∴FG≈2.165 m.
∴DM=FG+GM-DF≈2.165+2.239-1.35≈3.05(m).
因此,篮框D 到地面的距离大约是3.05 m.
解:
小试牛刀
4 如图,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10 m的A 处,测得一辆汽车从B 处行驶到C 处所用时间为0.9 s,已知∠B=30°,∠C=45°.
(1)求B,C 之间的距离(保留根号).
(2)如果此地限速为80 km/h,那么这辆汽车是否超速?请说明理由(参考数据: ≈1.7, ≈1.4).
小试牛刀
(1)如图,作AD⊥BC 于D,则AD=10 m.
在Rt△ACD 中,∵∠C=45°,
∴AD=CD=10 m.
在Rt△ABD 中,∵∠B=30°,
∴tan 30°=
∴BD= AD=10 m.
∴BC=BD+DC=(10+10 ) m,即B,C 之间的距离为(10+10 )m.
解:
小试牛刀
(2)这辆汽车超速.
理由:∵BC=10+10 ≈27(m),
∴汽车速度为 =30(m/s)=108(km/h).
∵108>80,∴这辆汽车超速.
小试牛刀
5 如图,某办公楼AB 的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2 m的影子CE,而当光线与地面夹角是45°时,办公楼顶A 在地面上的影子F 与墙角C 有25 m的距离(B,F,C 在一条直线上).
小试牛刀
(1)求办公楼AB 的高度;
(2)若要在A,E 之间挂一些彩旗,请你求出A,E 之间的距离
(参考数据:sin 22°≈ ,cos 22°≈ ,tan22°≈ ).
小试牛刀
(1)如图.过点E 作EM⊥AB,垂足为M.
设AB 为x m.在Rt△ABF 中,∠AFB=45°,
∴BF=AB=x m.
∴BC=BF+FC=(x+25)m.
在Rt△AEM 中,∠AEM=22°,AM=AB-BM=AB-CE=(x-2)m,ME=BC=(x+25)m,
tan22°= 解得x≈20,
即办公楼AB 的高度约为20 m.
解:
小试牛刀
(2)由(1)可得ME=x+25≈20+25=45(m).
在Rt△AME 中,cos22°=
∴AE=
即A,E 之间的距离约为48 m.
小试牛刀
6 如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD )靠墙摆放,高AD=80 cm,宽AB=48 cm,小强身高166 cm,下半身FG=100 cm,洗漱时下半身与地面成80°( ∠FGK=80°) ,身体前倾成125°
(∠EFG=125°),脚与洗漱台距离GC=15 cm(点D,C,G,K在同一直线上).
小试牛刀
(1)此时小强头部E 点与地面DK 相距多少?
(2)小强希望他的头部E 恰好在洗漱盆AB 的中点O 的正上方,
他应向前或后退多少?(sin 80°≈ 0.98,cos 80°≈0.17,
≈1.41,结果精确到0.1 cm)
小试牛刀
(1)如图,过点F 作FN⊥DK 于点N,过点E 作EM⊥FN 于点M.
∵EF+FG=166 cm,FG=100 cm,
∴EF=66 cm.
∵∠FGK=80°,
∴FN=100 sin 80°≈98(cm).
∵∠EFG=125°,
∴∠EFM=180°-125°-10°=45°.
∴FM=66 cos 45°=33 ≈46.53(cm).
∴MN=FN+FM≈98+46.53≈144.5(cm).
∴此时小强头部E 点与地面DK 大约相距144.5 cm.
解:
小试牛刀
(2)如图,过点E 作EP⊥AB 于点P,延长OB 交MN 于点H.
∵AB=48 cm,O 为AB 中点,
∴AO=BO=24 cm.
∵EM=66 sin 45°=33 ≈46.53(cm),
∴PH≈46.53 cm.
∵GN=100 cos 80°≈17(cm),GC=15 cm,
∴OH≈24+15+17=56(cm),OP=OH-PH≈56-46.53=9.47≈9.5(cm).
∴他应向前约9.5 cm.
课堂小结
课堂小结
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5 三角函数的应用
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.解直角三角形的意义:在直角三角形中,由已知元素
求出所有未知元素的过程,叫做直角三角形.
2.直角三角形中诸元素之间的关系:
(1)三边之间的关系:a 2+b 2=c 2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
把∠A 换成∠B 同样适用.
新课精讲
探索新知
1
知识点
借助工具测量的应用
想一想
如图,小明想测量塔CD 的高度.他在A 处仰望塔顶,
测得仰角为30°,再往塔的方向前 进50m至B 处,测得仰角
为60°,那么该塔有多高?
(小明的身高忽略不计,结
果精确到1m)
探索新知
1.运用锐角三角函数解决实际问题的方法:
(1)弄清题意,画出示意图;
(2)找出图形中的线段、角所表示的实际意义,并找到所要解决的问题;
(3)寻找要求解的直角三角形,有时需要作适当的辅助线;
(4)选择合适的边角关系式,进行有关锐角三角函数的计算;
(5)按照题目要求的精确度确定答案,并注明单位,作答.
探索新知
例1 “中国益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥.如图,新大桥的两端位于A,B 两点,小张为了测量A,B 之间的河宽,在垂直于新大桥AB 的直线形道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82 m.求AB 的长.(结果精确到0.1 m.参考数据:sin 76.1°≈0.97,
cos 76.1°≈0.24,tan 76.1°≈4.0;
sin 68.2°≈0.93,cos 68.2°≈0.37,
tan 68.2°≈2.5)
探索新知
设AD=x m,在Rt△ABC 中,利用∠BCA 的正切值,可以用含x 的代数式表示AB. 同理在Rt△ABD 中,利用∠BDA 的正切值表示出AB,从而列出关于x 的方程,求出x 的值就能求出AB 的长了.
导引:
探索新知
设AD=x m,则AC=(x+82) m.
在Rt△ABC 中,tan ∠BCA=
∴AB=AC · tan ∠BCA=(x+82)tan 68.2° m.
在Rt△ABD 中,tan ∠BDA=
∴AB=AD · tan ∠BDA=x tan 76.1° m.
∴(x+82)tan 68.2°=x tan 76.1°. ∴x≈136.67.
∴AB≈4×136.67≈546.7(m).
即AB 的长约为546.7 m.
解:
典题精讲
某楼梯的侧面如图所示,已测得BC 的长约为3.5米,∠BCA 约为29°,则该楼梯的高度AB 可表示为( )
A.3.5sin 29°米
B.3.5cos 29°米
C.3.5tan 29°米
D. 米
1
A
典题精讲
如图,AB 是斜靠在墙上的长梯,D 是梯上一点,梯脚B 与墙脚的距离为1.6 m(即BC 的长),点D 与墙的距离为1.4 m(即DE 的长),BD 长为0.55 m,则梯子的长为( )
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
2
B
典题精讲
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA 的高度与拉绳PB 的长度相等.小明将PB 拉到PB ′的位置,测得∠PB′C=α (B′C 为水平线),测角仪B′D 的高度为1 m,则旗杆PA 的高度为( )
B.
C. D.
3
A
探索新知
2
知识点
借助影子测量的应用
例2 如图,一幢楼房AB 背后有一台阶CD,台阶每层高0.2 m,且
AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°
时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在
台阶的MN 这层上晒太阳( 取1.73).
(1)求楼房的高度约为多少米.
(2)过了一会儿,当α=45°时,
问小猫还能否晒到太阳?
请说明理由.
探索新知
(1)当α=60°时,在Rt△ABE 中,
∵tan 60°=
∴AB=10·tan 60°=10 ≈10×1.73=17.3(m).
即楼房的高度约为17.3 m.
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:假设没有台阶,当α=45°时,从点B 射下的光线与地面AD 的交点为点F,与射线CM 的交点为点H (如下图).
解:
探索新知
∵∠BFA=45°,
∴tan 45°= =1,此时的影长AF=AB≈17.3m.
∴CF=AF-AC≈17.3-17.2=0.1(m).∴CH=CF≈0.1 m.
∴大楼的影子落在台阶MC 这个侧面上,
∴小猫仍可以晒到太阳.
典题精讲
如图,AB 是伸缩式遮阳棚,CD 是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB 的长是________米.(假设夏至的正午时刻阳光与地平面的夹角为60°)
典题精讲
如图,已知电线杆AB 直立于地面上,它的影子恰好
照在土坡的坡面CD 和地面BC 上,如果CD 与地面成
45°,∠A=60°,CD=4 m,BC=(4 -2 ) m,
则电线杆AB 的长为________.
易错提醒
如图,某海岛上的观察所A 发现海上某船只B,并测得其俯角α= 8°35′ .已知观察所 A 的标高(当水位为 0 m时的高度) 为45.54 m,当时水位为+2.34 m.求观察所A 与船只B 的水平距离(结果保留整数,参考数据:sin8°35′≈0.149,cos 8°35′≈0.989,tan 8°35′≈0.151).
易错点:忽略求正切值的前提.
易错提醒
由题意可知AC=45.54-2.34=43.2(m).
在Rt△ABC 中,∠ABC=α=8°35′,
tan ∠ABC=
∴BC=
因此观察所A 与船只B 的水平距离约为286 m.
易错总结:解题时容易弄错AC 的高度,A 处的标高为45.54 m(水位为0 m时的高度),当水位为+2.34 m时,即水位上升了2.34 m,则AC 的高度为45.54-2.34=43.2(m).
解:
学以致用
小试牛刀
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD (D 为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
1
C
小试牛刀
如图,要在宽为22 m的九州大道两边安装路灯,路灯的灯臂CD 长2 m,且与灯柱BC 成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO 与灯臂CD 垂直,当灯罩的轴线DO 通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC 高度应该设计为( )
A.(11-2 ) m
B.(11 -2 ) m
C.(11-2 ) m
D.(11 -4) m
2
D
小试牛刀
3 如图①②分别是某款篮球架的实物图与示意图,已知底座BC=0.60 m,底座BC 与支架AC 所成的角∠ACB=75°,支架AF 的长为2.50 m,篮板顶端F 点到篮框D 的距离FD=1.35 m,篮板底部支架HE 与支架AF 所成的角∠FHE=60°,求篮框D 到地面的距离(结果精确到0.01 m,参考数据:cos 75°≈0.258 8,sin 75°≈0.965 9,tan 75°≈3.732,3≈1.732,2≈1.414)
小试牛刀
如图,延长FE 交CB 于点M,过点A 作AG⊥FM 于点G.
在Rt△ABC 中,tan∠ACB=
∴AB=BC tan 75°≈0.60×3.732≈2.239(m).
∴GM=AB≈2.239 m.
在Rt△AGF 中,∵∠FAG=∠FHE=60°,
sin∠FAG= 即sin 60°=
∴FG≈2.165 m.
∴DM=FG+GM-DF≈2.165+2.239-1.35≈3.05(m).
因此,篮框D 到地面的距离大约是3.05 m.
解:
小试牛刀
4 如图,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10 m的A 处,测得一辆汽车从B 处行驶到C 处所用时间为0.9 s,已知∠B=30°,∠C=45°.
(1)求B,C 之间的距离(保留根号).
(2)如果此地限速为80 km/h,那么这辆汽车是否超速?请说明理由(参考数据: ≈1.7, ≈1.4).
小试牛刀
(1)如图,作AD⊥BC 于D,则AD=10 m.
在Rt△ACD 中,∵∠C=45°,
∴AD=CD=10 m.
在Rt△ABD 中,∵∠B=30°,
∴tan 30°=
∴BD= AD=10 m.
∴BC=BD+DC=(10+10 ) m,即B,C 之间的距离为(10+10 )m.
解:
小试牛刀
(2)这辆汽车超速.
理由:∵BC=10+10 ≈27(m),
∴汽车速度为 =30(m/s)=108(km/h).
∵108>80,∴这辆汽车超速.
小试牛刀
5 如图,某办公楼AB 的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2 m的影子CE,而当光线与地面夹角是45°时,办公楼顶A 在地面上的影子F 与墙角C 有25 m的距离(B,F,C 在一条直线上).
小试牛刀
(1)求办公楼AB 的高度;
(2)若要在A,E 之间挂一些彩旗,请你求出A,E 之间的距离
(参考数据:sin 22°≈ ,cos 22°≈ ,tan22°≈ ).
小试牛刀
(1)如图.过点E 作EM⊥AB,垂足为M.
设AB 为x m.在Rt△ABF 中,∠AFB=45°,
∴BF=AB=x m.
∴BC=BF+FC=(x+25)m.
在Rt△AEM 中,∠AEM=22°,AM=AB-BM=AB-CE=(x-2)m,ME=BC=(x+25)m,
tan22°= 解得x≈20,
即办公楼AB 的高度约为20 m.
解:
小试牛刀
(2)由(1)可得ME=x+25≈20+25=45(m).
在Rt△AME 中,cos22°=
∴AE=
即A,E 之间的距离约为48 m.
小试牛刀
6 如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD )靠墙摆放,高AD=80 cm,宽AB=48 cm,小强身高166 cm,下半身FG=100 cm,洗漱时下半身与地面成80°( ∠FGK=80°) ,身体前倾成125°
(∠EFG=125°),脚与洗漱台距离GC=15 cm(点D,C,G,K在同一直线上).
小试牛刀
(1)此时小强头部E 点与地面DK 相距多少?
(2)小强希望他的头部E 恰好在洗漱盆AB 的中点O 的正上方,
他应向前或后退多少?(sin 80°≈ 0.98,cos 80°≈0.17,
≈1.41,结果精确到0.1 cm)
小试牛刀
(1)如图,过点F 作FN⊥DK 于点N,过点E 作EM⊥FN 于点M.
∵EF+FG=166 cm,FG=100 cm,
∴EF=66 cm.
∵∠FGK=80°,
∴FN=100 sin 80°≈98(cm).
∵∠EFG=125°,
∴∠EFM=180°-125°-10°=45°.
∴FM=66 cos 45°=33 ≈46.53(cm).
∴MN=FN+FM≈98+46.53≈144.5(cm).
∴此时小强头部E 点与地面DK 大约相距144.5 cm.
解:
小试牛刀
(2)如图,过点E 作EP⊥AB 于点P,延长OB 交MN 于点H.
∵AB=48 cm,O 为AB 中点,
∴AO=BO=24 cm.
∵EM=66 sin 45°=33 ≈46.53(cm),
∴PH≈46.53 cm.
∵GN=100 cos 80°≈17(cm),GC=15 cm,
∴OH≈24+15+17=56(cm),OP=OH-PH≈56-46.53=9.47≈9.5(cm).
∴他应向前约9.5 cm.
课堂小结
课堂小结
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
