【班海精品】北师大版(新)九年级下-1.5三角函数的应用 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-1.5三角函数的应用 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览








文档简介
(共43张PPT)
5 三角函数的应用
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
直角三角形中诸元素之间的关系:
(1)三边之间的关系:a 2+b 2=c 2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
新课精讲
探索新知
1
知识点
用解直角三角形解方位角问题
方位角的定义:
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
探索新知
东
西
北
南
O
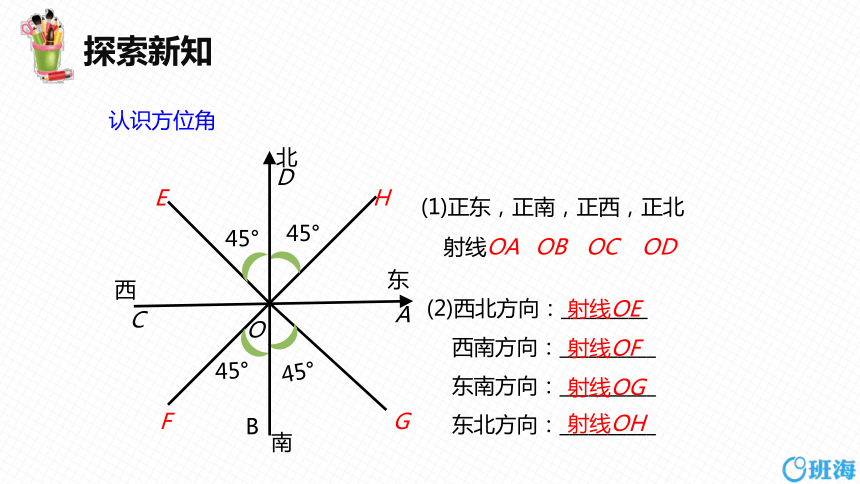
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
认识方位角
探索新知
O
北
南
西
东
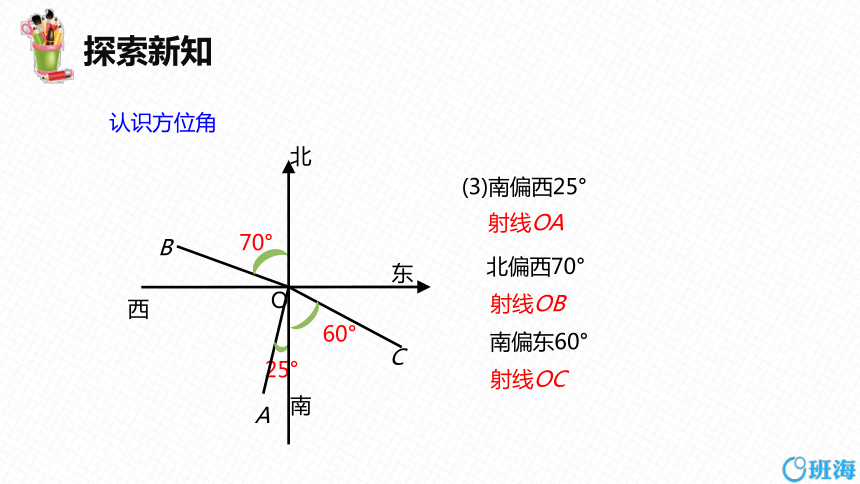
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
认识方位角
探索新知
如图,一艘海轮位于灯塔P 的 北偏东65°方向,距离灯塔80 n mile的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东34°方向上的B 处.这时,B 处距离灯塔P 有多远(结果取整数)?
A
P
C
B
北
例1
65°
34°
探索新知
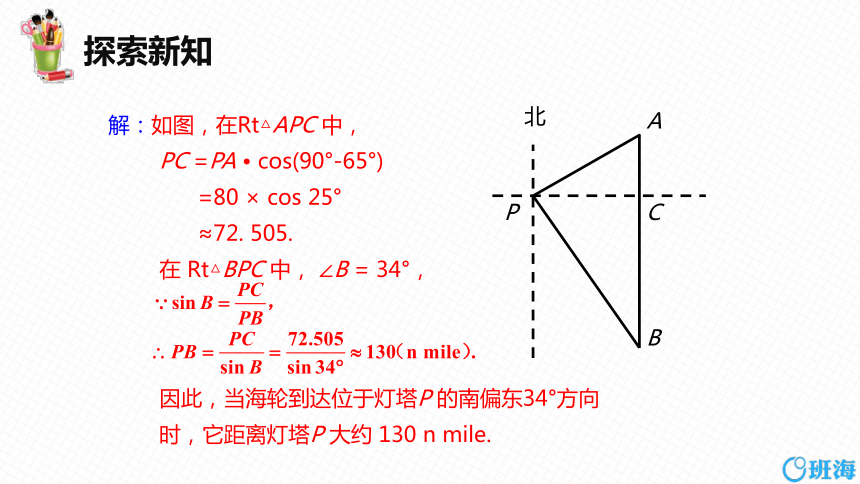
解:如图,在Rt△APC 中,
PC =PA cos(90°-65°)
=80 × cos 25°
≈72. 505.
在 Rt△BPC 中, ∠B = 34°,
因此,当海轮到达位于灯塔P 的南偏东34°方向
时,它距离灯塔P 大约 130 n mile.
A
P
C
B
北
探索新知
总 结
利用解直角三角形解决方向角的问题时,“同方向的方向线互相平行”是其中的一个隐含条件.
典题精讲
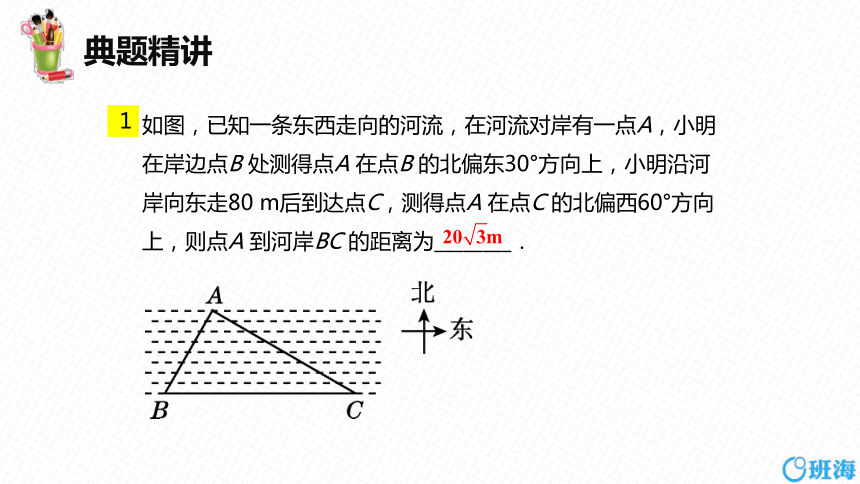
如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B 处测得点A 在点B 的北偏东30°方向上,小明沿河岸向东走80 m后到达点C,测得点A 在点C 的北偏西60°方向上,则点A 到河岸BC 的距离为________.
1
典题精讲
2 如图,一艘海轮位于灯塔P 的北偏东55°方向,距离灯塔2海里的A 处.如果海轮沿正南方向航行到灯塔的正东位置,则海轮航行的距离AB 是( )
A.2海里
B.2sin 55°海里
C.2cos 55°海里
D.2tan 55°海里
C
典题精讲
如图,一艘轮船在A 处测得灯塔P 位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B 处后,此时测得灯塔P 位于其北偏东30°方向上,此时轮船与灯塔P 的距离是( )
A.15 海里
B.30海里
C.45海里
D.30 海里
3
B
探索新知
2
知识点
用解直角三角形解坡角问题
α
A
C
B
D
E
坡面AB 与水平面的夹角叫做坡角.
坡面的垂直高度与水平
宽度之比叫做坡度,记作 i .
h
l
探索新知
例2 如图,一居民楼底部B 与山脚P 位于同一水平线上,小李在P 处
测得居民楼顶A 的仰角为60°,然后他从P 处沿坡角为45°的山坡
向上走到C 处,这时,PC=30 m,点C 与点A 在同一水平线上,
A,B,P,C 在同一平面内.
(1)求居民楼AB 的高度;
(2)求C,A 之间的距离.
(结果精确到0.1 m,
参考数据: ≈1.41,
≈1.73, ≈2.45)
探索新知
(1)过点C 作CE⊥BP,交BP 的延长线于点E,
易知AB=EC. 在Rt△CPE 中,由sin ∠CPE=
得出EC 的长度,进而可求出答案.
(2)在Rt△ABP 中,由tan ∠APB= 得出BP 的长,
在Rt△CPE 中,由cos ∠CPE=
得出PE 的长,最后由AC=BE=BP+PE 得出答案.
导引:
探索新知
(1)过点C 作CE⊥BP,交BP 的延长线于点E,如图,
易得AB=CE.
在Rt△CPE 中,PC=30 m,∠CPE=45°,
∵sin ∠CPE=
∴CE=PC · sin ∠CPE
=30×
≈21.2(m).
∴AB=CE≈21.2 m.
即居民楼AB 的高度约为21.2 m.
解:
探索新知
(2)在Rt△ABP 中,AB=152 m,∠APB=60°,
∴BP=
在Rt△CPE 中,PC=30 m,∠CPE=45°,
∴PE=PC · cos ∠CPE=30×
易得AC=BE=BP+PE=5 +15 ≈33.4(m),
即C,A 之间的距离约为33.4 m.
探索新知
总 结
作辅助线构造直角三角形解答,注意准确把握仰角及坡角的概念.
典题精讲
如图,水库大坝的横截面是梯形ABCD,其中AD//BC,坝顶AD= 6m坡长 CD = 8m,坡底BC=30m, ∠ADC=135°.
(1)求∠ABC 的度数;
(2 )如果坝长100 m,那么建筑这个大坝共需多少土石料?(结果精确到0.01 m3)
1
A
B
C
D
典题精讲
(1) 过点A 作AE⊥BC 于点E,过点D 作DF⊥BC 于点F.
∵AD∥BC,∴四边形AEFD 是矩形.
∴AD=EF,AE=DF.
∵∠ADC=135°,∴∠FDC=45°.
在Rt△DCF 中,DF=CD cos ∠FDC=8×cos 45°= (m),
FC=CD sin ∠FDC=8×sin 45°= (m),
∴BE=BC-EF-FC=30-6- =(24- ) m.
在Rt△ABE 中,tan ∠ABE= = =
≈0.308 4,∴∠ABC≈17°8′23″.
解:
典题精讲
(2) S四边形ABCD= (AD+BC )×DF
= ×(6+30)×
= (m2),
V= ×100≈10 182.34(m3).
所以,建筑这个大坝共需约10 182.34 m3土石料.
解:
典题精讲
如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A 滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
2
280
典题精讲
为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD. 已知迎水坡面AB=12米,背水坡面CD=123米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tan E= ,则CE 的长为_______.
3
8m
典题精讲
如图,小王在长江边某瞭望台D 处,测得江面上的渔船A 的俯角为40°,若DE=3米,CE=2米,CE 平行于江面AB,迎水坡BC 的坡度i=1∶0.75,坡长BC=10米,则此时AB 的长约为( )(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
A.5.1米
B.6.3米
C.7.1米
D.9.2米
4
A
典题精讲
如图,斜面AC 的坡度(CD 与AD 的比)为1:2,AC=3 米,坡顶有一旗杆BC,旗杆顶端B 点与A 点有一条彩带相连.若AB=10米,则旗杆BC 的高度为( )
A.5米
B.6米
C.8米
D.(3+ )米
5
A
学以致用
小试牛刀
如图,在距离铁轨200米的B 处,观察由南宁开往百色的“和谐号”动车,当动车车头在A 处时,恰好位于B 处的北偏东60°方向上;10秒钟后,动车车头到达C 处,恰好位于B 处的西北方向上,则这时段动车的平均速度是( )米/秒.
A.20( +1)
B.20( -1)
C.200
D.300
1
A
小试牛刀
如图,某人在大楼30米高(即PH=30米)的窗口P 处进行观测,测得山坡上A 处的俯角为15°,山脚B 处的俯角为60°,已知该山坡的坡度i 为1 : 点P,H,B,C,A 在同一个平面内,点H,B,C 在同一条直线上,且PH⊥HC.则A,B 两点间的距离是( )
A.15米
B.20 米
C.20 米
D.10 米
2
B
小试牛刀
3 如图,一艘轮船位于灯塔P 南偏西60°方向的A 处,它向东航行20 n mile到达灯塔P 南偏西45°方向上的B 处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P 的最短距离(结果保留根号).
小试牛刀
如图,作PC⊥AB 交AB 的延长线于点C,
则∠APC=60°,
∠BPC=45°,AB=20.
∴PC=BC,
AC=PC tan 60°= PC.
∴AB=AC-BC=( -1) PC=20.
∴PC= =10 +10(n mile).
答:轮船航行途中与灯塔P 的最短距离是(10 +10)n mile.
解:
小试牛刀
4 如图,港口B 位于港口A 的南偏东37°方向,灯塔C 恰好在AB 的中点处,一艘海轮位于港口A 的正南方向,港口B 的正西方向的D 处,它沿正北方向航行5 km到达E 处,测得灯塔C 在北偏东45°方向上,这时,E 处距离港口A 有多远?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
小试牛刀
如图,作CH⊥AD 于点H.设CH=x,
在Rt△ACH 中,∠A=37°,
tan 37°=
∴AH=
在Rt△CEH 中,
∵∠CEH=45°,
∴CH=EH=x.
∵CH⊥AD,BD⊥AD,
解:
小试牛刀
∴CH∥BD,
∴
∵AC=CB,∴AH=HD.
∴ =x+5.
∴x≈15.
∴AE=AH+HE= +15≈35(km),
∴E 处距离港口A 约35 km.
小试牛刀
5 为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2 m(即CD=2 m),背水坡DE 的坡度i=1∶1(即DB∶EB=1∶1),如图所示,已知AE=4 m,∠EAC=130°,求水坝原来的高度BC (参考数据:
sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.2).
小试牛刀
设BC=x,在Rt△ABC 中,
∠CAB=180°-∠EAC=50°,
∴AB=
在Rt△EBD 中,
i=DB∶EB=1∶1,∴BD=BE.
∴CD+BC=AE+AB,
即2+x=4+ x,解得x=12.
解:
小试牛刀
6 如图,某校教学楼AB 后方有一斜坡,已知斜坡CD 的长为12 m,坡角α 为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD 进行改造,在保持坡脚C 不动的情况下,学校至少要把坡顶D 向后水平移动多少米才能保证教学楼的安全?(结果取整数,参考数据:sin 39°≈0.63,cos 39°≈0.78,
tan 39°≈0.81, ≈1.41,
≈1.73, ≈2.24)
小试牛刀
假设点D 移到D ′的位置时,恰好∠α=39°,过点D 作DE⊥AC 于点E,过点D ′作D′E ′⊥AC 于点E ′,如图所示.
∵CD=12,∠DCE=60°,
∴DE=CD sin 60°=12× =6 ,
CE=CD cos 60°=12× =6.
∵DE⊥AC,D′E ′⊥AC,DD ′∥CE ′,
∴四边形DEE′D ′是矩形.
∴D′E ′=DE=6 .
∵∠D′CE ′=39°,
解:
小试牛刀
∴CE ′=
∴EE ′=CE ′-CE=12.8-6=6.8≈7(m).
答:学校至少要把坡顶D 向后水平移动7m才能保证教学楼的安全.
课堂小结
课堂小结
1.解决与方位角有关的实际问题时,必须先在每个位
置中心建立方向标,然后根据方位角标出图中已知
角的度数,最后在某个直角三角形内利用锐角三角
函数解决问题.
2.解决坡度问题时,可适当添加辅助线,将梯形分割
为直角三角形和矩形来解决问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5 三角函数的应用
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
直角三角形中诸元素之间的关系:
(1)三边之间的关系:a 2+b 2=c 2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
新课精讲
探索新知
1
知识点
用解直角三角形解方位角问题
方位角的定义:
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
探索新知
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
认识方位角
探索新知
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
认识方位角
探索新知
如图,一艘海轮位于灯塔P 的 北偏东65°方向,距离灯塔80 n mile的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东34°方向上的B 处.这时,B 处距离灯塔P 有多远(结果取整数)?
A
P
C
B
北
例1
65°
34°
探索新知
解:如图,在Rt△APC 中,
PC =PA cos(90°-65°)
=80 × cos 25°
≈72. 505.
在 Rt△BPC 中, ∠B = 34°,
因此,当海轮到达位于灯塔P 的南偏东34°方向
时,它距离灯塔P 大约 130 n mile.
A
P
C
B
北
探索新知
总 结
利用解直角三角形解决方向角的问题时,“同方向的方向线互相平行”是其中的一个隐含条件.
典题精讲
如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B 处测得点A 在点B 的北偏东30°方向上,小明沿河岸向东走80 m后到达点C,测得点A 在点C 的北偏西60°方向上,则点A 到河岸BC 的距离为________.
1
典题精讲
2 如图,一艘海轮位于灯塔P 的北偏东55°方向,距离灯塔2海里的A 处.如果海轮沿正南方向航行到灯塔的正东位置,则海轮航行的距离AB 是( )
A.2海里
B.2sin 55°海里
C.2cos 55°海里
D.2tan 55°海里
C
典题精讲
如图,一艘轮船在A 处测得灯塔P 位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B 处后,此时测得灯塔P 位于其北偏东30°方向上,此时轮船与灯塔P 的距离是( )
A.15 海里
B.30海里
C.45海里
D.30 海里
3
B
探索新知
2
知识点
用解直角三角形解坡角问题
α
A
C
B
D
E
坡面AB 与水平面的夹角叫做坡角.
坡面的垂直高度与水平
宽度之比叫做坡度,记作 i .
h
l
探索新知
例2 如图,一居民楼底部B 与山脚P 位于同一水平线上,小李在P 处
测得居民楼顶A 的仰角为60°,然后他从P 处沿坡角为45°的山坡
向上走到C 处,这时,PC=30 m,点C 与点A 在同一水平线上,
A,B,P,C 在同一平面内.
(1)求居民楼AB 的高度;
(2)求C,A 之间的距离.
(结果精确到0.1 m,
参考数据: ≈1.41,
≈1.73, ≈2.45)
探索新知
(1)过点C 作CE⊥BP,交BP 的延长线于点E,
易知AB=EC. 在Rt△CPE 中,由sin ∠CPE=
得出EC 的长度,进而可求出答案.
(2)在Rt△ABP 中,由tan ∠APB= 得出BP 的长,
在Rt△CPE 中,由cos ∠CPE=
得出PE 的长,最后由AC=BE=BP+PE 得出答案.
导引:
探索新知
(1)过点C 作CE⊥BP,交BP 的延长线于点E,如图,
易得AB=CE.
在Rt△CPE 中,PC=30 m,∠CPE=45°,
∵sin ∠CPE=
∴CE=PC · sin ∠CPE
=30×
≈21.2(m).
∴AB=CE≈21.2 m.
即居民楼AB 的高度约为21.2 m.
解:
探索新知
(2)在Rt△ABP 中,AB=152 m,∠APB=60°,
∴BP=
在Rt△CPE 中,PC=30 m,∠CPE=45°,
∴PE=PC · cos ∠CPE=30×
易得AC=BE=BP+PE=5 +15 ≈33.4(m),
即C,A 之间的距离约为33.4 m.
探索新知
总 结
作辅助线构造直角三角形解答,注意准确把握仰角及坡角的概念.
典题精讲
如图,水库大坝的横截面是梯形ABCD,其中AD//BC,坝顶AD= 6m坡长 CD = 8m,坡底BC=30m, ∠ADC=135°.
(1)求∠ABC 的度数;
(2 )如果坝长100 m,那么建筑这个大坝共需多少土石料?(结果精确到0.01 m3)
1
A
B
C
D
典题精讲
(1) 过点A 作AE⊥BC 于点E,过点D 作DF⊥BC 于点F.
∵AD∥BC,∴四边形AEFD 是矩形.
∴AD=EF,AE=DF.
∵∠ADC=135°,∴∠FDC=45°.
在Rt△DCF 中,DF=CD cos ∠FDC=8×cos 45°= (m),
FC=CD sin ∠FDC=8×sin 45°= (m),
∴BE=BC-EF-FC=30-6- =(24- ) m.
在Rt△ABE 中,tan ∠ABE= = =
≈0.308 4,∴∠ABC≈17°8′23″.
解:
典题精讲
(2) S四边形ABCD= (AD+BC )×DF
= ×(6+30)×
= (m2),
V= ×100≈10 182.34(m3).
所以,建筑这个大坝共需约10 182.34 m3土石料.
解:
典题精讲
如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A 滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
2
280
典题精讲
为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD. 已知迎水坡面AB=12米,背水坡面CD=123米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tan E= ,则CE 的长为_______.
3
8m
典题精讲
如图,小王在长江边某瞭望台D 处,测得江面上的渔船A 的俯角为40°,若DE=3米,CE=2米,CE 平行于江面AB,迎水坡BC 的坡度i=1∶0.75,坡长BC=10米,则此时AB 的长约为( )(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
A.5.1米
B.6.3米
C.7.1米
D.9.2米
4
A
典题精讲
如图,斜面AC 的坡度(CD 与AD 的比)为1:2,AC=3 米,坡顶有一旗杆BC,旗杆顶端B 点与A 点有一条彩带相连.若AB=10米,则旗杆BC 的高度为( )
A.5米
B.6米
C.8米
D.(3+ )米
5
A
学以致用
小试牛刀
如图,在距离铁轨200米的B 处,观察由南宁开往百色的“和谐号”动车,当动车车头在A 处时,恰好位于B 处的北偏东60°方向上;10秒钟后,动车车头到达C 处,恰好位于B 处的西北方向上,则这时段动车的平均速度是( )米/秒.
A.20( +1)
B.20( -1)
C.200
D.300
1
A
小试牛刀
如图,某人在大楼30米高(即PH=30米)的窗口P 处进行观测,测得山坡上A 处的俯角为15°,山脚B 处的俯角为60°,已知该山坡的坡度i 为1 : 点P,H,B,C,A 在同一个平面内,点H,B,C 在同一条直线上,且PH⊥HC.则A,B 两点间的距离是( )
A.15米
B.20 米
C.20 米
D.10 米
2
B
小试牛刀
3 如图,一艘轮船位于灯塔P 南偏西60°方向的A 处,它向东航行20 n mile到达灯塔P 南偏西45°方向上的B 处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P 的最短距离(结果保留根号).
小试牛刀
如图,作PC⊥AB 交AB 的延长线于点C,
则∠APC=60°,
∠BPC=45°,AB=20.
∴PC=BC,
AC=PC tan 60°= PC.
∴AB=AC-BC=( -1) PC=20.
∴PC= =10 +10(n mile).
答:轮船航行途中与灯塔P 的最短距离是(10 +10)n mile.
解:
小试牛刀
4 如图,港口B 位于港口A 的南偏东37°方向,灯塔C 恰好在AB 的中点处,一艘海轮位于港口A 的正南方向,港口B 的正西方向的D 处,它沿正北方向航行5 km到达E 处,测得灯塔C 在北偏东45°方向上,这时,E 处距离港口A 有多远?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
小试牛刀
如图,作CH⊥AD 于点H.设CH=x,
在Rt△ACH 中,∠A=37°,
tan 37°=
∴AH=
在Rt△CEH 中,
∵∠CEH=45°,
∴CH=EH=x.
∵CH⊥AD,BD⊥AD,
解:
小试牛刀
∴CH∥BD,
∴
∵AC=CB,∴AH=HD.
∴ =x+5.
∴x≈15.
∴AE=AH+HE= +15≈35(km),
∴E 处距离港口A 约35 km.
小试牛刀
5 为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2 m(即CD=2 m),背水坡DE 的坡度i=1∶1(即DB∶EB=1∶1),如图所示,已知AE=4 m,∠EAC=130°,求水坝原来的高度BC (参考数据:
sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.2).
小试牛刀
设BC=x,在Rt△ABC 中,
∠CAB=180°-∠EAC=50°,
∴AB=
在Rt△EBD 中,
i=DB∶EB=1∶1,∴BD=BE.
∴CD+BC=AE+AB,
即2+x=4+ x,解得x=12.
解:
小试牛刀
6 如图,某校教学楼AB 后方有一斜坡,已知斜坡CD 的长为12 m,坡角α 为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD 进行改造,在保持坡脚C 不动的情况下,学校至少要把坡顶D 向后水平移动多少米才能保证教学楼的安全?(结果取整数,参考数据:sin 39°≈0.63,cos 39°≈0.78,
tan 39°≈0.81, ≈1.41,
≈1.73, ≈2.24)
小试牛刀
假设点D 移到D ′的位置时,恰好∠α=39°,过点D 作DE⊥AC 于点E,过点D ′作D′E ′⊥AC 于点E ′,如图所示.
∵CD=12,∠DCE=60°,
∴DE=CD sin 60°=12× =6 ,
CE=CD cos 60°=12× =6.
∵DE⊥AC,D′E ′⊥AC,DD ′∥CE ′,
∴四边形DEE′D ′是矩形.
∴D′E ′=DE=6 .
∵∠D′CE ′=39°,
解:
小试牛刀
∴CE ′=
∴EE ′=CE ′-CE=12.8-6=6.8≈7(m).
答:学校至少要把坡顶D 向后水平移动7m才能保证教学楼的安全.
课堂小结
课堂小结
1.解决与方位角有关的实际问题时,必须先在每个位
置中心建立方向标,然后根据方位角标出图中已知
角的度数,最后在某个直角三角形内利用锐角三角
函数解决问题.
2.解决坡度问题时,可适当添加辅助线,将梯形分割
为直角三角形和矩形来解决问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
