【班海精品】北师大版(新)九年级下-2.2二次函数的图象与性质 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-2.2二次函数的图象与性质 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览









文档简介
(共42张PPT)
2 二次函数的图象与性质
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)一次函数的图象是什么?
一条直线
(2)画函数图象的基本方法与步骤是什么?
列表——描点——连线
(3)研究函数时,主要用什么来了解函数的性质呢?
主要工具是函数的图象
回顾旧知
新课精讲
探索新知
1
知识点
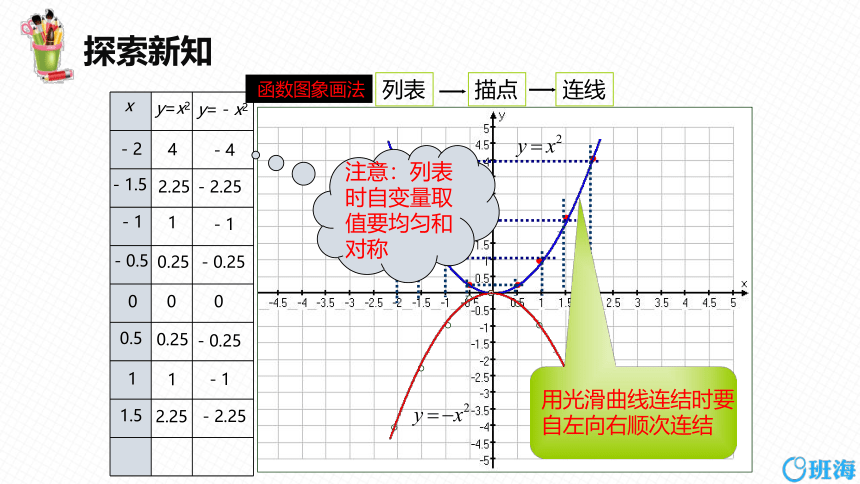
二次函数 y = x 2与 y = -x 2的图象
在同一直角坐标系中,画出函数 y = x 2 和 y =-x 2 的图象,这两个函数的图象相比, 有什么共同点?有什么不同点?
探索新知
y=x2
y=-x2
0
0.25
1
2.25
0.25
1
2.25
4
0
-0.25
-1
-2.25
-0.25
-1
-2.25
-4
x
0
-2
1
1.5
0.5
-1.5
-0.5
-1
函数图象画法
列表
描点
连线
注意:列表
时自变量取
值要均匀和
对称
用光滑曲线连结时要
自左向右顺次连结
探索新知
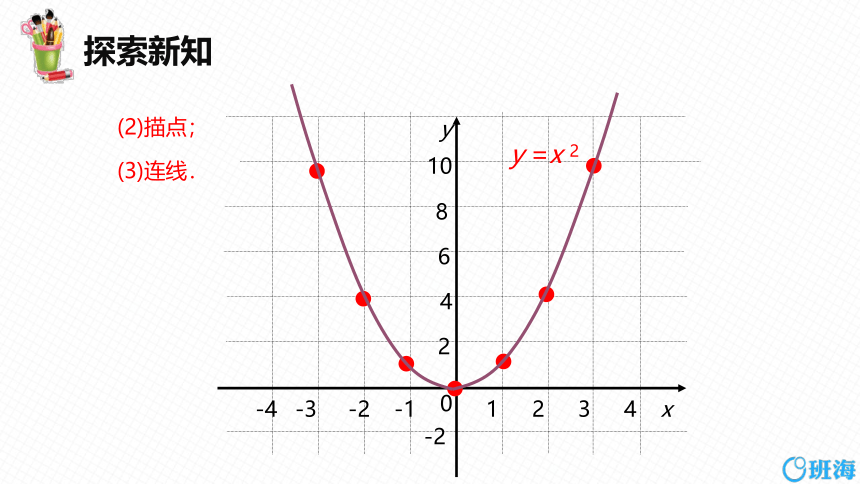
例1 作出二次函数 y=x 2的图象.
按列表、描点、连线三个步骤画函数的图象.
(1)列表:
x … -3 -2 -1 0 1 2 3 …
y … 9 4 1 0 1 4 9 …
解:
导引:
探索新知
(2)描点;
(3)连线.
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
y =x 2
探索新知
总 结
七点法,即先取原点,然后在原点两侧对称地取六个点,由于关于y 轴对称的两个点的横坐标互为相反数,纵坐标相等,所以先计算y 轴右侧三个点的坐标,则左侧三个点的坐标对应写出即可.
典题精讲
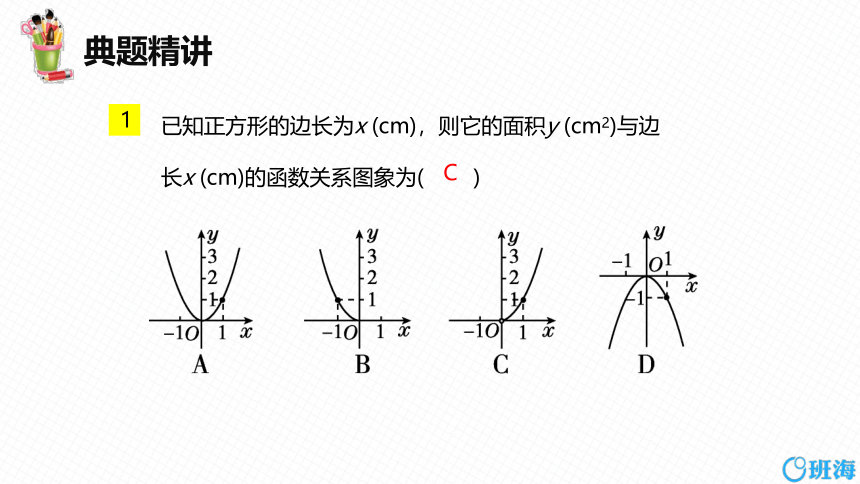
已知正方形的边长为x (cm),则它的面积y (cm2)与边长x (cm)的函数关系图象为( )
1
C
典题精讲
下列关于抛物线 y=x 2和y=-x 2的异同点说法错误的是( )
A.抛物线 y=x 2和y=-x 2有共同的顶点和对称轴
B.抛物线 y=x 2和y=-x 2的开口方向相反
C.抛物线 y=x 2和y=-x 2关于x 轴成轴对称
D.点A(-3,9)在抛物线 y=x 2上,也在抛物线 y=-x 2上
2
D
典题精讲
关于y=x 2与 y=-x 2的图象,下列说法中错误的是( )
A.其形状相同,但开口方向相反,原因是函数
表达式的系数互为相反数
B.都关于y 轴对称
C.图象都有最低点,且其坐标均为(0,0)
D.两图象关于x 轴对称
3
C
典题精讲
已知A (m,a )和B (n,a )两点都在抛物线 y=x 2上,则m,n 之间的关系正确的是( )
A.m=n
B.m+n=0
C.m+n>0
D.m+n<0
4
B
典题精讲
2
知识点
二次函数 y = x 2与 y = -x 2的性质
议一议
观察二次函数 y=x 2与 y =-x 2的图象,你能发现什么问题?
探索新知
抛物线
y =x 2
y =-x 2
顶点坐标
对称轴
位置
开口方向
极值
(0,0)
(0,0)
y 轴
y 轴
在x 轴的上方(除顶点外)
在x 轴的下方(除顶点外)
向上
向下
当x =0时,最小值为0.
当x =0时,最大值为0.
探索新知
当a>0时,在对称轴的
左侧,y 随着x 的增大而
减小。
当a>0时,在对称轴的
右侧,y 随着x 的增大而
增大。
当a<0时,在对称轴的
左侧,y 随着x 的增大而
增大。
当a<0时,在对称轴的
右侧,y 随着x 的增大而
减小。
当x=-2时,y=4
当x=-1时,y=1
当x =1时,y =1
当x =2时,y =4
当x=-2时,y=-4
当x=-1时,y=-1
当x =1时,y =-1
当x =2时,y =-4
探索新知
例2 已知函数 y=- x 2,不画图象,回答下列各题.
(1)开口方向:______;
(2)对称轴:_____;
(3)顶点坐标:______;
(4)当x>0时,y 随x 的增大而______;
(5)当x____时,y=0;
(6)当x____时,函数值 y 最____,是___.
导引:根据二次函数 y=ax 2(a≠0)的性质直接作答.
向下
y 轴
减小
(0,0)
=0
=0
大
0
探索新知
例3 如图,观察函数 y=x 2的图象,则下列判断中正确
的是( )
A.若a,b 互为相反数,则当x=a 与x=b 时的函数
值相等
B.对于同一个自变量x,有
两个函数值与其对应
C.对任意实数 x,都有y>0
D.对任意实数 y,都有两个x
与其对应
A
探索新知
导引:当x=a 和x=b 时的函数值分别是a 2,b 2,因为a=-b,
所以a 2=b 2,所以A正确.如果对于同一个自变量x,y 有
两个值与其对应,根据定义知 y 就不是 x 的函数,故B错误.
当x=0时,y=0,所以选项C也不对.y=x 2的图象是经过原
点,位于x 轴上方的,所以y ≥0,y 不可能取到所有实数,当
y=0时,x=0,故D错误.
探索新知
总 结
y=x 2的图象关键有两性:
一是对称性(关于y 轴对称);
二是非负性(函数值 y 的非负性).
探索新知
例4 已知a>1,点(a-1,y1),(a,y2),(a+1,y3)都在函数 y=x 2
的图象上,则y1,y2,y3 之间的大小关系为___________.
导引:
因为a>1,所以00时,y 随x 的增大而增大”的性质,可得y3>y2>y1.
y3>y2>y1
探索新知
总 结
当所比较的点都在抛物线的对称轴的同一侧时,可直接利用函数的增减性进行大小比较.
典题精讲
已知点(x1,y1),(x2,y2)是二次函数 y=-x 2的图象上的两点,当x11
y1<y2
如图,点A 是抛物线 y=-x 2上一点,AB⊥x 轴于点B,连接AO,若B点坐标为(-2,0),则A点坐标为____________,S△AOB=________.
2
(-2,-4)
4
典题精讲
下列说法正确的是( )
A.函数 y=x 2的图象上的点,其纵坐标的值随x 值的增
大而增大
B.函数 y=-x 2的图象上的点,其纵坐标的值随x 值的
增大而增大
C.抛物线y=x 2与y=-x 2的开口方向不同,其对称轴
都是y 轴,且y 值都随x 值的增大而增大
D.当x<0时,函数 y=x 2,y 的值随x 值的增大的变化情
况与当x >0时,函数y=-x 2,y 的值随x 值的增大的
变化情况相同
3
D
典题精讲
如图,一次函数 y1=kx+b 的图象与二次函数 y2=x 2的图象交于A (-1,1)和B (2,4)两点,则当y1A.x<-1
B.x >2
C.-1D.x<-1或x >2
4
D
易错小结
函数 y=-x 2(-2≤x≤1)的最大值为____,最小值为______.
易错点:求函数的最值问题时忽略自变量的取值范围.
0
-4
学以致用
小试牛刀
已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数 y=x 2的图象上,则( )
A.y1<y2<y3
B.y1<y3<y2
C.y3<y2<y1
D.y2<y1<y3
1
C
小试牛刀
如图,圆的半径为2,C1 是函数 y=x 2的图象,C2 是函数y=-x 2的图象,则阴影部分的面积是________.
2
2π
小试牛刀
3 已知函数 y=(m+2)x +4m+5是关于x 的二次函数.
(1)求满足条件的m 的值.
(2)当m 为何值时,抛物线有最高点?求出这个最高点的坐标.
小试牛刀
(1)根据题意有
解得
即当m=-3或m=-1时,函数y=(m+2)x +4m+5是关于x 的二次函数.
(2)∵抛物线有最高点,∴m+2<0,
即m<-2.则m=-3.
此时二次函数表达式为y=-x 2,
其图象的最高点的坐标为(0,0).
解:
m+2≠0,
m 2+4m+5=2.
m≠-2,
m=-3或m=-1.
小试牛刀
4 已知抛物线 y=-x 2与直线 y=3x+m 都经过点(2,n).
(1)画出函数 y=-x 2的图象,并求出m,n 的值.
(2)两者是否存在另一个交点?若存在,请求出这个点的坐标;若不存在,请说明理由.
小试牛刀
(1)函数 y=-x 2的图象如图所示.
∵抛物线 y=-x 2与直线 y=3x+m 都过点(2,n),
∴n=-22,n=3×2+m,即n=-4,m=-10.
(2)存在.
联立方程组
解得 或
则另一个交点的坐标为(-5,-25).
解:
y=-x 2,
y=3x-10,
x=-5,
y=-25
x=2,
y=-4.
小试牛刀
5 已知点A (1,a )在抛物线 y=x 2上.
(1)求点A 的坐标.
(2)在x 轴上是否存在点P,使得△OAP 是等腰三角形?若存在,求出点P 的坐标; 若不存在,请说明理由.
小试牛刀
(1)把点(1,a)的坐标代入y=x 2,
得a=1,所以点A 的坐标为(1,1).
(2)存在.当OA=AP 时,点P 的坐标为(2,0);当OA=OP 时,点P 的坐标为( ,0)或(- ,0);当OP=AP 时,点P 的坐标为(1,0).
解:
小试牛刀
6 有一抛物线型城门洞,拱高为4 m,如图,把它放在平面直角坐标系中,其函数表达式为 y=-x 2.
(1)求城门洞最宽处AB 的长;
(2)现有一辆高为2.6 m,宽为2.2 m的小型货车,问它能否安全通过此城门洞?
小试牛刀
(1)因为点O 到AB 的距离为4 m,所以A,B 两点的纵坐标都为-4,由-4=-x 2,得x=±2.又点A 在点B 左侧,则点A 的坐标为(-2,-4),点B 的坐标为(2,-4).所以AB=4 m.即城门洞最宽处AB 的长为4 m.
解:
小试牛刀
(2)如图,用矩形CDEF 表示小型货车的横截面,则ED,FC 均垂直于AB,点E,F 到AB 的距离为2.6 m,点F 的横坐标为1.1.设拋物线上一点M 的横坐标为1.1,则点M 的纵坐标为-1.12=-1.21,所以点M 到AB 的距离为4-|-1.21|=2.79(m).因为2.79>2.6,所以小型货车能安全通过此城门洞.
课堂小结
课堂小结
1.研究函数图象,就是要明确该函数图象的画法、名称、形状特征以及分布在坐标系中的位置.二次函数 y=x 2和y=-x 2的图象都是抛物线,是轴对称图形.开口方向、顶点、对称轴统称为抛物线的三要素.
2.二次函数 y=x 2和 y=-x 2图象的形状和大小完全相同,只是开口方向不同,这两个函数的图象既关于x 轴对称又关于原点对称.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2 二次函数的图象与性质
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)一次函数的图象是什么?
一条直线
(2)画函数图象的基本方法与步骤是什么?
列表——描点——连线
(3)研究函数时,主要用什么来了解函数的性质呢?
主要工具是函数的图象
回顾旧知
新课精讲
探索新知
1
知识点
二次函数 y = x 2与 y = -x 2的图象
在同一直角坐标系中,画出函数 y = x 2 和 y =-x 2 的图象,这两个函数的图象相比, 有什么共同点?有什么不同点?
探索新知
y=x2
y=-x2
0
0.25
1
2.25
0.25
1
2.25
4
0
-0.25
-1
-2.25
-0.25
-1
-2.25
-4
x
0
-2
1
1.5
0.5
-1.5
-0.5
-1
函数图象画法
列表
描点
连线
注意:列表
时自变量取
值要均匀和
对称
用光滑曲线连结时要
自左向右顺次连结
探索新知
例1 作出二次函数 y=x 2的图象.
按列表、描点、连线三个步骤画函数的图象.
(1)列表:
x … -3 -2 -1 0 1 2 3 …
y … 9 4 1 0 1 4 9 …
解:
导引:
探索新知
(2)描点;
(3)连线.
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
y =x 2
探索新知
总 结
七点法,即先取原点,然后在原点两侧对称地取六个点,由于关于y 轴对称的两个点的横坐标互为相反数,纵坐标相等,所以先计算y 轴右侧三个点的坐标,则左侧三个点的坐标对应写出即可.
典题精讲
已知正方形的边长为x (cm),则它的面积y (cm2)与边长x (cm)的函数关系图象为( )
1
C
典题精讲
下列关于抛物线 y=x 2和y=-x 2的异同点说法错误的是( )
A.抛物线 y=x 2和y=-x 2有共同的顶点和对称轴
B.抛物线 y=x 2和y=-x 2的开口方向相反
C.抛物线 y=x 2和y=-x 2关于x 轴成轴对称
D.点A(-3,9)在抛物线 y=x 2上,也在抛物线 y=-x 2上
2
D
典题精讲
关于y=x 2与 y=-x 2的图象,下列说法中错误的是( )
A.其形状相同,但开口方向相反,原因是函数
表达式的系数互为相反数
B.都关于y 轴对称
C.图象都有最低点,且其坐标均为(0,0)
D.两图象关于x 轴对称
3
C
典题精讲
已知A (m,a )和B (n,a )两点都在抛物线 y=x 2上,则m,n 之间的关系正确的是( )
A.m=n
B.m+n=0
C.m+n>0
D.m+n<0
4
B
典题精讲
2
知识点
二次函数 y = x 2与 y = -x 2的性质
议一议
观察二次函数 y=x 2与 y =-x 2的图象,你能发现什么问题?
探索新知
抛物线
y =x 2
y =-x 2
顶点坐标
对称轴
位置
开口方向
极值
(0,0)
(0,0)
y 轴
y 轴
在x 轴的上方(除顶点外)
在x 轴的下方(除顶点外)
向上
向下
当x =0时,最小值为0.
当x =0时,最大值为0.
探索新知
当a>0时,在对称轴的
左侧,y 随着x 的增大而
减小。
当a>0时,在对称轴的
右侧,y 随着x 的增大而
增大。
当a<0时,在对称轴的
左侧,y 随着x 的增大而
增大。
当a<0时,在对称轴的
右侧,y 随着x 的增大而
减小。
当x=-2时,y=4
当x=-1时,y=1
当x =1时,y =1
当x =2时,y =4
当x=-2时,y=-4
当x=-1时,y=-1
当x =1时,y =-1
当x =2时,y =-4
探索新知
例2 已知函数 y=- x 2,不画图象,回答下列各题.
(1)开口方向:______;
(2)对称轴:_____;
(3)顶点坐标:______;
(4)当x>0时,y 随x 的增大而______;
(5)当x____时,y=0;
(6)当x____时,函数值 y 最____,是___.
导引:根据二次函数 y=ax 2(a≠0)的性质直接作答.
向下
y 轴
减小
(0,0)
=0
=0
大
0
探索新知
例3 如图,观察函数 y=x 2的图象,则下列判断中正确
的是( )
A.若a,b 互为相反数,则当x=a 与x=b 时的函数
值相等
B.对于同一个自变量x,有
两个函数值与其对应
C.对任意实数 x,都有y>0
D.对任意实数 y,都有两个x
与其对应
A
探索新知
导引:当x=a 和x=b 时的函数值分别是a 2,b 2,因为a=-b,
所以a 2=b 2,所以A正确.如果对于同一个自变量x,y 有
两个值与其对应,根据定义知 y 就不是 x 的函数,故B错误.
当x=0时,y=0,所以选项C也不对.y=x 2的图象是经过原
点,位于x 轴上方的,所以y ≥0,y 不可能取到所有实数,当
y=0时,x=0,故D错误.
探索新知
总 结
y=x 2的图象关键有两性:
一是对称性(关于y 轴对称);
二是非负性(函数值 y 的非负性).
探索新知
例4 已知a>1,点(a-1,y1),(a,y2),(a+1,y3)都在函数 y=x 2
的图象上,则y1,y2,y3 之间的大小关系为___________.
导引:
因为a>1,所以0
y3>y2>y1
探索新知
总 结
当所比较的点都在抛物线的对称轴的同一侧时,可直接利用函数的增减性进行大小比较.
典题精讲
已知点(x1,y1),(x2,y2)是二次函数 y=-x 2的图象上的两点,当x1
y1<y2
如图,点A 是抛物线 y=-x 2上一点,AB⊥x 轴于点B,连接AO,若B点坐标为(-2,0),则A点坐标为____________,S△AOB=________.
2
(-2,-4)
4
典题精讲
下列说法正确的是( )
A.函数 y=x 2的图象上的点,其纵坐标的值随x 值的增
大而增大
B.函数 y=-x 2的图象上的点,其纵坐标的值随x 值的
增大而增大
C.抛物线y=x 2与y=-x 2的开口方向不同,其对称轴
都是y 轴,且y 值都随x 值的增大而增大
D.当x<0时,函数 y=x 2,y 的值随x 值的增大的变化情
况与当x >0时,函数y=-x 2,y 的值随x 值的增大的
变化情况相同
3
D
典题精讲
如图,一次函数 y1=kx+b 的图象与二次函数 y2=x 2的图象交于A (-1,1)和B (2,4)两点,则当y1
B.x >2
C.-1
4
D
易错小结
函数 y=-x 2(-2≤x≤1)的最大值为____,最小值为______.
易错点:求函数的最值问题时忽略自变量的取值范围.
0
-4
学以致用
小试牛刀
已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数 y=x 2的图象上,则( )
A.y1<y2<y3
B.y1<y3<y2
C.y3<y2<y1
D.y2<y1<y3
1
C
小试牛刀
如图,圆的半径为2,C1 是函数 y=x 2的图象,C2 是函数y=-x 2的图象,则阴影部分的面积是________.
2
2π
小试牛刀
3 已知函数 y=(m+2)x +4m+5是关于x 的二次函数.
(1)求满足条件的m 的值.
(2)当m 为何值时,抛物线有最高点?求出这个最高点的坐标.
小试牛刀
(1)根据题意有
解得
即当m=-3或m=-1时,函数y=(m+2)x +4m+5是关于x 的二次函数.
(2)∵抛物线有最高点,∴m+2<0,
即m<-2.则m=-3.
此时二次函数表达式为y=-x 2,
其图象的最高点的坐标为(0,0).
解:
m+2≠0,
m 2+4m+5=2.
m≠-2,
m=-3或m=-1.
小试牛刀
4 已知抛物线 y=-x 2与直线 y=3x+m 都经过点(2,n).
(1)画出函数 y=-x 2的图象,并求出m,n 的值.
(2)两者是否存在另一个交点?若存在,请求出这个点的坐标;若不存在,请说明理由.
小试牛刀
(1)函数 y=-x 2的图象如图所示.
∵抛物线 y=-x 2与直线 y=3x+m 都过点(2,n),
∴n=-22,n=3×2+m,即n=-4,m=-10.
(2)存在.
联立方程组
解得 或
则另一个交点的坐标为(-5,-25).
解:
y=-x 2,
y=3x-10,
x=-5,
y=-25
x=2,
y=-4.
小试牛刀
5 已知点A (1,a )在抛物线 y=x 2上.
(1)求点A 的坐标.
(2)在x 轴上是否存在点P,使得△OAP 是等腰三角形?若存在,求出点P 的坐标; 若不存在,请说明理由.
小试牛刀
(1)把点(1,a)的坐标代入y=x 2,
得a=1,所以点A 的坐标为(1,1).
(2)存在.当OA=AP 时,点P 的坐标为(2,0);当OA=OP 时,点P 的坐标为( ,0)或(- ,0);当OP=AP 时,点P 的坐标为(1,0).
解:
小试牛刀
6 有一抛物线型城门洞,拱高为4 m,如图,把它放在平面直角坐标系中,其函数表达式为 y=-x 2.
(1)求城门洞最宽处AB 的长;
(2)现有一辆高为2.6 m,宽为2.2 m的小型货车,问它能否安全通过此城门洞?
小试牛刀
(1)因为点O 到AB 的距离为4 m,所以A,B 两点的纵坐标都为-4,由-4=-x 2,得x=±2.又点A 在点B 左侧,则点A 的坐标为(-2,-4),点B 的坐标为(2,-4).所以AB=4 m.即城门洞最宽处AB 的长为4 m.
解:
小试牛刀
(2)如图,用矩形CDEF 表示小型货车的横截面,则ED,FC 均垂直于AB,点E,F 到AB 的距离为2.6 m,点F 的横坐标为1.1.设拋物线上一点M 的横坐标为1.1,则点M 的纵坐标为-1.12=-1.21,所以点M 到AB 的距离为4-|-1.21|=2.79(m).因为2.79>2.6,所以小型货车能安全通过此城门洞.
课堂小结
课堂小结
1.研究函数图象,就是要明确该函数图象的画法、名称、形状特征以及分布在坐标系中的位置.二次函数 y=x 2和y=-x 2的图象都是抛物线,是轴对称图形.开口方向、顶点、对称轴统称为抛物线的三要素.
2.二次函数 y=x 2和 y=-x 2图象的形状和大小完全相同,只是开口方向不同,这两个函数的图象既关于x 轴对称又关于原点对称.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
