【班海精品】北师大版(新)九年级下-3.1圆【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-3.1圆【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览











文档简介
(共49张PPT)
1 圆
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
新课精讲
探索新知
1
知识点
圆的定义
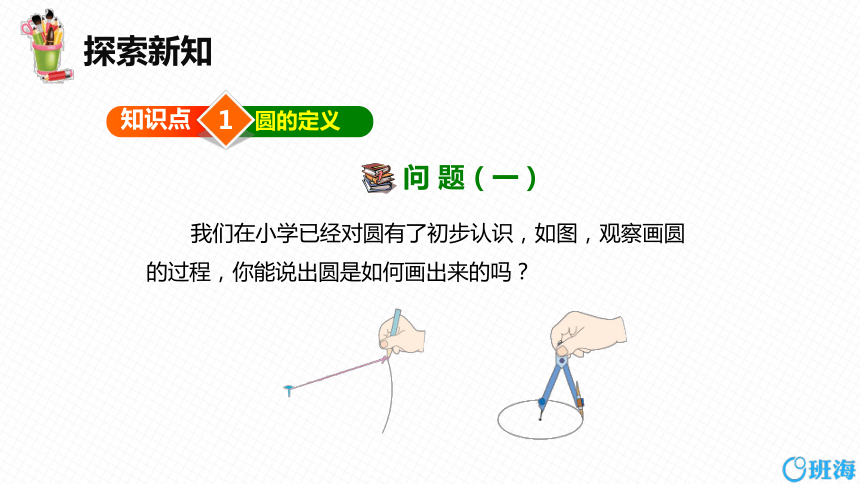
问 题(一)
我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?
探索新知
归 纳
在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.其固定的端点 O 叫做圆心线段 OA 叫做半径. 以点 O 为圆心的圆,记作⊙O,读作“圆O ”.
探索新知
问 题(二)
从画圆的过程可以看出什么呢?
(1)圆上各点到定点(圆心O)的距离都等于定长(半径r);
(2)到定点的距离等于定长的点都在同一个圆上.
在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另
一个端点A 所形成的图形叫做圆.
圆心为O、半径为r 的圆可以看成是所有到定点O 的距离等于定
长r 的点组成的图形.
思考:
解答:
动态:
静态:
探索新知
归 纳
圆心为O、半径为r 的圆可以看成是所有到定点O 的距离等于定长r 的点的集合.
确定一个圆的两个要素:圆心、半径.圆心确定圆的位置,半径确定圆的大小.
探索新知
下列说法中,错误的有( )
(1)经过点P 的圆有无数个;
(2)以点P 为圆心的圆有无数个;
(3)半径为3 cm且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm为半径的圆有无数个.
A.1个 B.2个 C.3个 D.4个
确定一个圆必须有两个条件,即圆心和半径,只满足一个条
件或不满足任何一个条件的圆都有无数个,由此可知(1)(2)
正确;(3)半径确定,但圆心不确定,仍有无数个圆;(4)圆
心和半径都确定的圆有且只有一个(唯一).
导引:
例1
A
探索新知
总 结
(1)圆的两种定义中确定圆的条件是相同的,即圆心和半径.两者缺一不可;
(2)“点在圆上”和“圆过点”表示的意义都是:这个点在圆周上.
特别提醒:圆是“圆周”,而非“圆面”.
典题精讲
体育老师想利用一根3 m长的绳子在操场上画一个半径为3 m的圆,你能帮他想想办法吗?
1
将绳子的一端A 固定,然后拉紧绳子的另一端B,并绕A 点在地上旋转一周,则B 点经过的路线就是一个半径为3 m的圆.
解:
下列图形中,四个顶点一定在同一个圆上的是( )
A.菱形、平行四边形
B.矩形、正方形
C.正方形、菱形
D.矩形、平行四边形
2
B
典题精讲
下列关于圆的叙述中正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.平面上到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
平面内已知点P,以P 为圆心,3 cm为半径作圆,这样的圆可以作( )
A.1个 B.2个 C.3个 D.无数个
3
4
B
A
探索新知
2
知识点
与圆有关的概念
弦:连接圆上任意两点的线段(如图中的AC)叫做弦,
经过圆心的弦(如图中的AB)叫做直径.
注意:
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是
圆中最长的弦,但弦不一定是直径.
C
A
·
O
B
探索新知
弧:圆上任意两点间的部分叫做圆弧,简称弧.如图,以A、B
为端点的弧记作 AB ,读作“圆弧AB ”或“弧AB ”.
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧
都叫做半圆.
⌒
·
C
O
A
B
探索新知
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
探索新知
等圆与等弧:
能够重合的两个圆叫做等圆.容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等. 在同圆或等圆中,能够互相重合的弧叫做等弧.
探索新知
以下命题:①半圆是弧,但弧不一定是半圆;②过圆上任意一点只能作一条弦,且这条弦是直径;③弦是直径;④直径是圆中最长的弦;⑤直径不是弦;⑥优弧大于劣弧; ⑦以O 为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
例2
C
探索新知
①弧分为劣弧、半圆、优弧三种,所以半圆是弧,但弧不一
定是半圆,故正确;②过圆上任意一点可以作无数条弦,故
错误;③直径是过圆心的特殊弦,但弦不一定是直径,故错
误;④圆有无数条弦,过圆心的弦最长,即直径是圆中最长
的弦,故正确;⑤直径是过圆心的弦,故错误;⑥在同圆或
等圆中,优弧大于劣弧,故错误;⑦以一个点为圆心,若不
指明半径,可画出无数个大小不等的同心圆,故正确.
导引:
探索新知
直径是过圆心的弦,因此直径是弦,但弦不一定是直径;在提到“弦”时,如果没有特别说明,不要忘记直径这种特殊的弦.
弦是圆上两点间的线
段,有无数条;弧是
圆上两点间的部分,
弧是曲线,弧也有无
数条.
每条弧对一条弦;而每条弦所对的弧有两条:优弧、劣弧或两个半圆.
弦与直径间的关系:
弦与弧之间的关系:
探索新知
如图 ,已知⊙O上有A,B,C 三个点,
以其中两个点为端点的弧共有_____条,
弦共有____条.
例3
由弧的概念知以A,B,C 中任意两个点为端点的弧有,
共6条;由弦的概念知以A,
B,C 中任意两个点为端点的弦有AB,BC,AC,共3条.
导引:
6
3
探索新知
总 结
圆上的任意两点分圆为两条弧:
一条优弧、一条劣弧或两个半圆,本题容易忽视圆中的优弧而造成得到3条弧的错误答案;在同圆中每段弧对应一条弦,而每条弦对应两条弧:一条优弧、一条劣弧或两个半圆.
典题精讲
下列说法中,正确的是( )
①弦是直径;②半圆是弧;③过圆心的线段是直径;④半圆是最长的弧;⑤直径是圆中最长的弦.
A.②③ B.③⑤ C.④⑤ D.②⑤
1
D
点A,C 为半径是3的圆周上两点,点B 为AC 的中点,以线段BA,BC 为邻边作菱形ABCD,顶点D 恰在该圆直径的三等分点上,则该菱形的边长为( )
A. 或2 B. 或2
C. 或2 D. 或2
2
︵
D
典题精讲
如图,点A,B,C 在⊙O 上,∠A=36°,∠C=28°,则∠B 等于( )
A.100°
B.72°
C.64°
D.36°
3
C
探索新知
3
知识点
点与圆的位置关系
如图所示, ⊙O 是一个半径为r 的圆.在圆内、 圆外、圆上分别取一点,点到圆心的距离为d, 你能用r 与 d 的大小关系刻画它们的位置特征吗?
.
O
探索新知
设⊙O 的半径为r,点P 到圆心的距离OP = d,则有:
点P 在圆外 d>r;
点P 在圆上 d=r;
点P 在圆内 d<r.
符号“ ”读作“等价于”,
它表示从符号“ ”的左
端可以推出右端,从右端也可以推出左端.
探索新知
归 纳
点与圆的位置关系有三种:
点在圆外、点在圆上、点在圆内.
探索新知
如图,在Rt△ABC 中,∠ACB=90°,CD⊥AB 于点D,∠A=30°,AC=3 cm.以C 为圆心, cm为半径画⊙C,请指出点A,B,D 与⊙C 的位置关系.
例4
探索新知
要判断点A,B,D 与⊙C 的位置关系,只需求出点A,B,
D 到点C 的距离,即AC,BC,CD 的长,并和半径
cm比较大小,进而得出结果.
解:
导引:
在Rt△ACD 中,∵∠A=30°,∴CD= AC= ×3=
1.5(cm).∵CD=1.5 cm< cm,∴点D 在⊙C 内部.
在Rt△ABC 中,∵∠A=30°,∴BC=AC · tan 30°=
3× = (cm).∴点B 在⊙C上.∵AC=3 cm>
cm,∴点A 在⊙C 外部.
探索新知
总 结
判断一个点与圆的位置关系,只需求出这个点到圆心的距离,然后和半径比较大小即可得解.
典题精讲
小明和小华正在练习投铅球,铅球场地分为五个区域:4m以内,4 5m,5 6m,6 7m,7m以 外.
小明投了 5.2 m,小华投了 6.7 m,他们投的球分别落在哪个区域内?
1
小明投的球落在5~6 m的区域内,小华投的球落在6~7 m的区域内.
解:
典题精讲
在公园的O 处附近有E,F,G,H 四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O 为圆心,OA 为半径的圆形水池,要求池中不留树木,则E,F,G,H 四棵树中需要被移除的为( )
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
2
A
典题精讲
如图,已知P 是⊙O 外一点,Q 是⊙O上的动点,线段PQ 的中点为M,连接OP,OM. 若⊙O 的半径为2,OP=4,则线段OM 的最小值是( )
A.0
B.1
C.2
D.3
3
B
易错提醒
若⊙O 所在平面内一点P 到⊙O上的点的最大距离为a,最小距离为b (a>b),则此圆的半径为( )
A. B.
C. D.a+b或a-b
易错点:考虑问题不全面而致错
C
学以致用
小试牛刀
如图,已知AC 是⊙O 的直径,点B 在圆周上(不与点A,C 重合),点D 在AC 的延长线上,连接BD 交⊙O 于点E,若∠AOB=3∠ADB,则( )
A.DE=EB
B. DE=EB
C. DE=DO
D.DE=OB
1
D
小试牛刀
如图,王大伯家屋后有一块长12 m,宽8 m的矩形空地,他在以长BC 为直径的半圆内种菜,他家养的一只羊平时拴在A 处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.3 m
B.5 m
C.7 m
D.9 m
2
A
小试牛刀
3 设AB=4 cm,作出满足下列要求的图形.
(1)到点A 的距离等于3 cm的所有点组成的图形,到点B 的距离等于2 cm的所有点组成的图形;
(2)到点A 的距离等于3 cm,且到点B 的距离等于2 cm的所有点组成的图形;
(3)到点A 的距离小于3 cm,且到点B 的距离小于2 cm的所有点组成的图形;
(4)到点A 的距离大于3 cm,且到点B 的距离小于2 cm的所有点组成的图形.
小试牛刀
(1)如图①,到点A 的距离等于3 cm的所有点组成的图形是以点A 为圆心,3 cm为半径的圆,到点B 的距离等于2 cm的所有点组成的图形是以点B 为圆心,2 cm为半径的圆.
解:
小试牛刀
(2)如图②,以点A 为圆心,3 cm为半径的⊙A 与以点B 为圆心,2 cm为半径的⊙B 的交点,即C,D 两点.
(3)如图③,以点A为圆心,3 cm为半径的⊙A 的内部与以点B 为圆心,2 cm为半径的⊙B 的内部的公共部分(不包括边界的阴影部分)即为所求.
(4)如图④,以点A 为圆心,3 cm为半径的⊙A 的外部与以点B为圆心,2 cm为半径的⊙B 的内部的公共部分(不包括边界的阴影部分)即为所求.
小试牛刀
4 如图,AB 是半圆O 的直径,四边形CDEF 是正方形.
(1)求证:OC=OF;
(2)在正方形CDEF 的右侧有一正方形FGHK,点G 在AB上,点H 在半圆上,点K 在EF上.若正方形CDEF 的边长为2,求正方形FGHK 的面积.
小试牛刀
如图,连接OD,OE,则OD=OE.
又∠OCD=∠OFE=90°,DC=EF,∴Rt△ODC ≌ Rt△OEF (HL),∴OC=OF.
如图,连接OH,
∵CF=EF=2,OC=OF,∴OF=1,
∴OH 2=OE 2=OF 2+EF 2=12+22=5.
设FG=GH=x,∵OG 2+GH 2=OH 2,
∴(x+1)2+x 2=5,∴x 2+x-2=0,
解得x1=1,x2=-2(舍去).
∴S正方形FGHK=12=1.
(1)证明:
(2)解:
小试牛刀
5 如图,已知矩形ABCD 的边AB=3 cm,AD=4 cm,
(1)若以点A 为圆心,4 cm为半径作⊙A,则点B,C,D 和⊙A 的位置关系如何?
(2)若以点A 为圆心作⊙A,使B,C,D 三点中至少有一点在⊙A 内且至少有一点在⊙A 外,则⊙A 的半径r 的取值范围是多少?
小试牛刀
(1)∵AB=3 cm<4 cm,
∴点B 在⊙A 内.
∵AD=4 cm,∴点D 在⊙A上.
如图,连接AC,∵∠B=90°,
∴AC=
∵5 cm>4 cm,∴点C 在⊙A 外.
(2)由题可知点B 一定在⊙A 内,点C 一定在⊙A 外,
∴AB<r<AC,即3 cm<r<5 cm.
∴满足条件的⊙A 的半径r 的取值范围是3 cm<r<5 cm.
解:
小试牛刀
6 如图,在城市A 的正北方向50 km的B 处有一座无线电信号发射塔.已知该发射塔发射的无线电信号的有效半径为100 km,AC 是一条从A城直达C 城的公路,从A 城发往C 城的班车速度为60 km/h.
(1)当班车从A 城出发开往C 城时,某人立即打开无线电收音机,班车行驶了0.5 h的时候,接收信号最强.信号最强时班车到发射塔的距离是多少千米?
(离发射塔越近,信号越强)
(2)班车从A 城到C 城共行驶2 h,请你
判断到C 城后还能接收到信号吗?请
说明理由.
小试牛刀
(1)设班车行驶了0.5 h的时候到达点M,连接BM. 根据此时接收信号最强,可知BM⊥AC. 而AM=0.5×60=30(km),
AB=50 km,所以BM=40 km.
即信号最强时班车到发射塔的距离是40 km.
(2)能.理由:
因为AC=60×2=120(km),AM=30 km,
所以MC=AC-AM=120-30=90(km).
连接BC.因为BM=40 km,所以在Rt△BMC 中,
由勾股定理得BC=
因为 <100,所以到C 城后能接收到信号.
解:
课堂小结
课堂小结
1.理解圆的定义要注意两层含义:
(1)静态定义
(2)动态定义.
2.与圆有关的概念
弦与直径,弧、半圆、优弧、劣弧,等圆与等弧,
3.点和圆的位置关系:点在圆外、点在圆上、点在圆内.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1 圆
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是常见的图形,生活中的许多物体都给我们以圆的形象(如图).
新课精讲
探索新知
1
知识点
圆的定义
问 题(一)
我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?
探索新知
归 纳
在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.其固定的端点 O 叫做圆心线段 OA 叫做半径. 以点 O 为圆心的圆,记作⊙O,读作“圆O ”.
探索新知
问 题(二)
从画圆的过程可以看出什么呢?
(1)圆上各点到定点(圆心O)的距离都等于定长(半径r);
(2)到定点的距离等于定长的点都在同一个圆上.
在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另
一个端点A 所形成的图形叫做圆.
圆心为O、半径为r 的圆可以看成是所有到定点O 的距离等于定
长r 的点组成的图形.
思考:
解答:
动态:
静态:
探索新知
归 纳
圆心为O、半径为r 的圆可以看成是所有到定点O 的距离等于定长r 的点的集合.
确定一个圆的两个要素:圆心、半径.圆心确定圆的位置,半径确定圆的大小.
探索新知
下列说法中,错误的有( )
(1)经过点P 的圆有无数个;
(2)以点P 为圆心的圆有无数个;
(3)半径为3 cm且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm为半径的圆有无数个.
A.1个 B.2个 C.3个 D.4个
确定一个圆必须有两个条件,即圆心和半径,只满足一个条
件或不满足任何一个条件的圆都有无数个,由此可知(1)(2)
正确;(3)半径确定,但圆心不确定,仍有无数个圆;(4)圆
心和半径都确定的圆有且只有一个(唯一).
导引:
例1
A
探索新知
总 结
(1)圆的两种定义中确定圆的条件是相同的,即圆心和半径.两者缺一不可;
(2)“点在圆上”和“圆过点”表示的意义都是:这个点在圆周上.
特别提醒:圆是“圆周”,而非“圆面”.
典题精讲
体育老师想利用一根3 m长的绳子在操场上画一个半径为3 m的圆,你能帮他想想办法吗?
1
将绳子的一端A 固定,然后拉紧绳子的另一端B,并绕A 点在地上旋转一周,则B 点经过的路线就是一个半径为3 m的圆.
解:
下列图形中,四个顶点一定在同一个圆上的是( )
A.菱形、平行四边形
B.矩形、正方形
C.正方形、菱形
D.矩形、平行四边形
2
B
典题精讲
下列关于圆的叙述中正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.平面上到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
平面内已知点P,以P 为圆心,3 cm为半径作圆,这样的圆可以作( )
A.1个 B.2个 C.3个 D.无数个
3
4
B
A
探索新知
2
知识点
与圆有关的概念
弦:连接圆上任意两点的线段(如图中的AC)叫做弦,
经过圆心的弦(如图中的AB)叫做直径.
注意:
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是
圆中最长的弦,但弦不一定是直径.
C
A
·
O
B
探索新知
弧:圆上任意两点间的部分叫做圆弧,简称弧.如图,以A、B
为端点的弧记作 AB ,读作“圆弧AB ”或“弧AB ”.
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧
都叫做半圆.
⌒
·
C
O
A
B
探索新知
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
探索新知
等圆与等弧:
能够重合的两个圆叫做等圆.容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等. 在同圆或等圆中,能够互相重合的弧叫做等弧.
探索新知
以下命题:①半圆是弧,但弧不一定是半圆;②过圆上任意一点只能作一条弦,且这条弦是直径;③弦是直径;④直径是圆中最长的弦;⑤直径不是弦;⑥优弧大于劣弧; ⑦以O 为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
例2
C
探索新知
①弧分为劣弧、半圆、优弧三种,所以半圆是弧,但弧不一
定是半圆,故正确;②过圆上任意一点可以作无数条弦,故
错误;③直径是过圆心的特殊弦,但弦不一定是直径,故错
误;④圆有无数条弦,过圆心的弦最长,即直径是圆中最长
的弦,故正确;⑤直径是过圆心的弦,故错误;⑥在同圆或
等圆中,优弧大于劣弧,故错误;⑦以一个点为圆心,若不
指明半径,可画出无数个大小不等的同心圆,故正确.
导引:
探索新知
直径是过圆心的弦,因此直径是弦,但弦不一定是直径;在提到“弦”时,如果没有特别说明,不要忘记直径这种特殊的弦.
弦是圆上两点间的线
段,有无数条;弧是
圆上两点间的部分,
弧是曲线,弧也有无
数条.
每条弧对一条弦;而每条弦所对的弧有两条:优弧、劣弧或两个半圆.
弦与直径间的关系:
弦与弧之间的关系:
探索新知
如图 ,已知⊙O上有A,B,C 三个点,
以其中两个点为端点的弧共有_____条,
弦共有____条.
例3
由弧的概念知以A,B,C 中任意两个点为端点的弧有,
共6条;由弦的概念知以A,
B,C 中任意两个点为端点的弦有AB,BC,AC,共3条.
导引:
6
3
探索新知
总 结
圆上的任意两点分圆为两条弧:
一条优弧、一条劣弧或两个半圆,本题容易忽视圆中的优弧而造成得到3条弧的错误答案;在同圆中每段弧对应一条弦,而每条弦对应两条弧:一条优弧、一条劣弧或两个半圆.
典题精讲
下列说法中,正确的是( )
①弦是直径;②半圆是弧;③过圆心的线段是直径;④半圆是最长的弧;⑤直径是圆中最长的弦.
A.②③ B.③⑤ C.④⑤ D.②⑤
1
D
点A,C 为半径是3的圆周上两点,点B 为AC 的中点,以线段BA,BC 为邻边作菱形ABCD,顶点D 恰在该圆直径的三等分点上,则该菱形的边长为( )
A. 或2 B. 或2
C. 或2 D. 或2
2
︵
D
典题精讲
如图,点A,B,C 在⊙O 上,∠A=36°,∠C=28°,则∠B 等于( )
A.100°
B.72°
C.64°
D.36°
3
C
探索新知
3
知识点
点与圆的位置关系
如图所示, ⊙O 是一个半径为r 的圆.在圆内、 圆外、圆上分别取一点,点到圆心的距离为d, 你能用r 与 d 的大小关系刻画它们的位置特征吗?
.
O
探索新知
设⊙O 的半径为r,点P 到圆心的距离OP = d,则有:
点P 在圆外 d>r;
点P 在圆上 d=r;
点P 在圆内 d<r.
符号“ ”读作“等价于”,
它表示从符号“ ”的左
端可以推出右端,从右端也可以推出左端.
探索新知
归 纳
点与圆的位置关系有三种:
点在圆外、点在圆上、点在圆内.
探索新知
如图,在Rt△ABC 中,∠ACB=90°,CD⊥AB 于点D,∠A=30°,AC=3 cm.以C 为圆心, cm为半径画⊙C,请指出点A,B,D 与⊙C 的位置关系.
例4
探索新知
要判断点A,B,D 与⊙C 的位置关系,只需求出点A,B,
D 到点C 的距离,即AC,BC,CD 的长,并和半径
cm比较大小,进而得出结果.
解:
导引:
在Rt△ACD 中,∵∠A=30°,∴CD= AC= ×3=
1.5(cm).∵CD=1.5 cm< cm,∴点D 在⊙C 内部.
在Rt△ABC 中,∵∠A=30°,∴BC=AC · tan 30°=
3× = (cm).∴点B 在⊙C上.∵AC=3 cm>
cm,∴点A 在⊙C 外部.
探索新知
总 结
判断一个点与圆的位置关系,只需求出这个点到圆心的距离,然后和半径比较大小即可得解.
典题精讲
小明和小华正在练习投铅球,铅球场地分为五个区域:4m以内,4 5m,5 6m,6 7m,7m以 外.
小明投了 5.2 m,小华投了 6.7 m,他们投的球分别落在哪个区域内?
1
小明投的球落在5~6 m的区域内,小华投的球落在6~7 m的区域内.
解:
典题精讲
在公园的O 处附近有E,F,G,H 四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O 为圆心,OA 为半径的圆形水池,要求池中不留树木,则E,F,G,H 四棵树中需要被移除的为( )
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
2
A
典题精讲
如图,已知P 是⊙O 外一点,Q 是⊙O上的动点,线段PQ 的中点为M,连接OP,OM. 若⊙O 的半径为2,OP=4,则线段OM 的最小值是( )
A.0
B.1
C.2
D.3
3
B
易错提醒
若⊙O 所在平面内一点P 到⊙O上的点的最大距离为a,最小距离为b (a>b),则此圆的半径为( )
A. B.
C. D.a+b或a-b
易错点:考虑问题不全面而致错
C
学以致用
小试牛刀
如图,已知AC 是⊙O 的直径,点B 在圆周上(不与点A,C 重合),点D 在AC 的延长线上,连接BD 交⊙O 于点E,若∠AOB=3∠ADB,则( )
A.DE=EB
B. DE=EB
C. DE=DO
D.DE=OB
1
D
小试牛刀
如图,王大伯家屋后有一块长12 m,宽8 m的矩形空地,他在以长BC 为直径的半圆内种菜,他家养的一只羊平时拴在A 处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.3 m
B.5 m
C.7 m
D.9 m
2
A
小试牛刀
3 设AB=4 cm,作出满足下列要求的图形.
(1)到点A 的距离等于3 cm的所有点组成的图形,到点B 的距离等于2 cm的所有点组成的图形;
(2)到点A 的距离等于3 cm,且到点B 的距离等于2 cm的所有点组成的图形;
(3)到点A 的距离小于3 cm,且到点B 的距离小于2 cm的所有点组成的图形;
(4)到点A 的距离大于3 cm,且到点B 的距离小于2 cm的所有点组成的图形.
小试牛刀
(1)如图①,到点A 的距离等于3 cm的所有点组成的图形是以点A 为圆心,3 cm为半径的圆,到点B 的距离等于2 cm的所有点组成的图形是以点B 为圆心,2 cm为半径的圆.
解:
小试牛刀
(2)如图②,以点A 为圆心,3 cm为半径的⊙A 与以点B 为圆心,2 cm为半径的⊙B 的交点,即C,D 两点.
(3)如图③,以点A为圆心,3 cm为半径的⊙A 的内部与以点B 为圆心,2 cm为半径的⊙B 的内部的公共部分(不包括边界的阴影部分)即为所求.
(4)如图④,以点A 为圆心,3 cm为半径的⊙A 的外部与以点B为圆心,2 cm为半径的⊙B 的内部的公共部分(不包括边界的阴影部分)即为所求.
小试牛刀
4 如图,AB 是半圆O 的直径,四边形CDEF 是正方形.
(1)求证:OC=OF;
(2)在正方形CDEF 的右侧有一正方形FGHK,点G 在AB上,点H 在半圆上,点K 在EF上.若正方形CDEF 的边长为2,求正方形FGHK 的面积.
小试牛刀
如图,连接OD,OE,则OD=OE.
又∠OCD=∠OFE=90°,DC=EF,∴Rt△ODC ≌ Rt△OEF (HL),∴OC=OF.
如图,连接OH,
∵CF=EF=2,OC=OF,∴OF=1,
∴OH 2=OE 2=OF 2+EF 2=12+22=5.
设FG=GH=x,∵OG 2+GH 2=OH 2,
∴(x+1)2+x 2=5,∴x 2+x-2=0,
解得x1=1,x2=-2(舍去).
∴S正方形FGHK=12=1.
(1)证明:
(2)解:
小试牛刀
5 如图,已知矩形ABCD 的边AB=3 cm,AD=4 cm,
(1)若以点A 为圆心,4 cm为半径作⊙A,则点B,C,D 和⊙A 的位置关系如何?
(2)若以点A 为圆心作⊙A,使B,C,D 三点中至少有一点在⊙A 内且至少有一点在⊙A 外,则⊙A 的半径r 的取值范围是多少?
小试牛刀
(1)∵AB=3 cm<4 cm,
∴点B 在⊙A 内.
∵AD=4 cm,∴点D 在⊙A上.
如图,连接AC,∵∠B=90°,
∴AC=
∵5 cm>4 cm,∴点C 在⊙A 外.
(2)由题可知点B 一定在⊙A 内,点C 一定在⊙A 外,
∴AB<r<AC,即3 cm<r<5 cm.
∴满足条件的⊙A 的半径r 的取值范围是3 cm<r<5 cm.
解:
小试牛刀
6 如图,在城市A 的正北方向50 km的B 处有一座无线电信号发射塔.已知该发射塔发射的无线电信号的有效半径为100 km,AC 是一条从A城直达C 城的公路,从A 城发往C 城的班车速度为60 km/h.
(1)当班车从A 城出发开往C 城时,某人立即打开无线电收音机,班车行驶了0.5 h的时候,接收信号最强.信号最强时班车到发射塔的距离是多少千米?
(离发射塔越近,信号越强)
(2)班车从A 城到C 城共行驶2 h,请你
判断到C 城后还能接收到信号吗?请
说明理由.
小试牛刀
(1)设班车行驶了0.5 h的时候到达点M,连接BM. 根据此时接收信号最强,可知BM⊥AC. 而AM=0.5×60=30(km),
AB=50 km,所以BM=40 km.
即信号最强时班车到发射塔的距离是40 km.
(2)能.理由:
因为AC=60×2=120(km),AM=30 km,
所以MC=AC-AM=120-30=90(km).
连接BC.因为BM=40 km,所以在Rt△BMC 中,
由勾股定理得BC=
因为 <100,所以到C 城后能接收到信号.
解:
课堂小结
课堂小结
1.理解圆的定义要注意两层含义:
(1)静态定义
(2)动态定义.
2.与圆有关的概念
弦与直径,弧、半圆、优弧、劣弧,等圆与等弧,
3.点和圆的位置关系:点在圆外、点在圆上、点在圆内.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
