【班海精品】北师大版(新)九年级下-3.4圆周角和圆心角的关系 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-3.4圆周角和圆心角的关系 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览







文档简介
(共43张PPT)
4 圆周角和圆心角的关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
1.什么叫做圆周角?
2.圆周角定理是什么?
3.圆周角定理的推论1的内容是什么?
新课精讲
探索新知
1
知识点
直径所对的圆周角是直角
直径所对的圆周角是多少度?请说明理由.
总结
直径所对的圆周角是直角.
探索新知
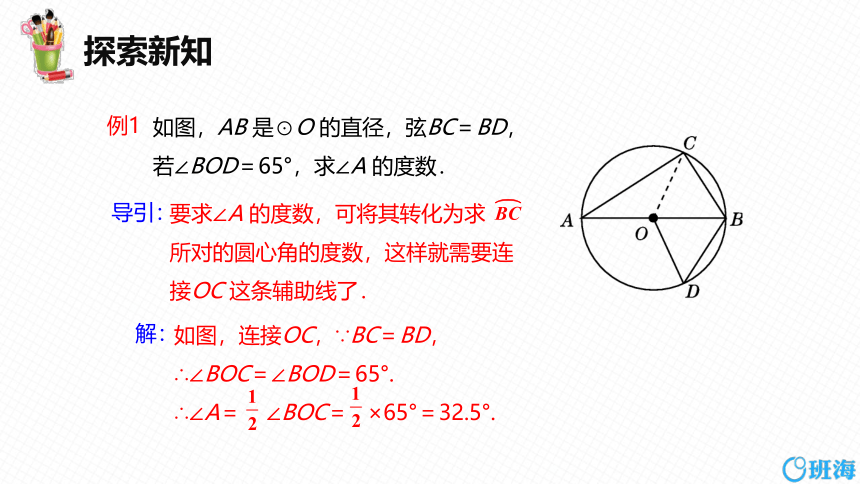
如图,AB 是⊙O 的直径,弦BC=BD,
若∠BOD=65°,求∠A 的度数.
要求∠A 的度数,可将其转化为求
所对的圆心角的度数,这样就需要连
接OC 这条辅助线了.
导引:
例1
如图,连接OC,∵BC=BD,
∴∠BOC=∠BOD=65°.
∴∠A= ∠BOC= ×65°=32.5°.
解:
探索新知
总 结
同圆或等圆中的弦、弧、圆心角、圆周角之间的关系可以互相转化,当某个结论不好求时,可运用转化思想将其转化为求与之相关的另一结论.
典题精讲
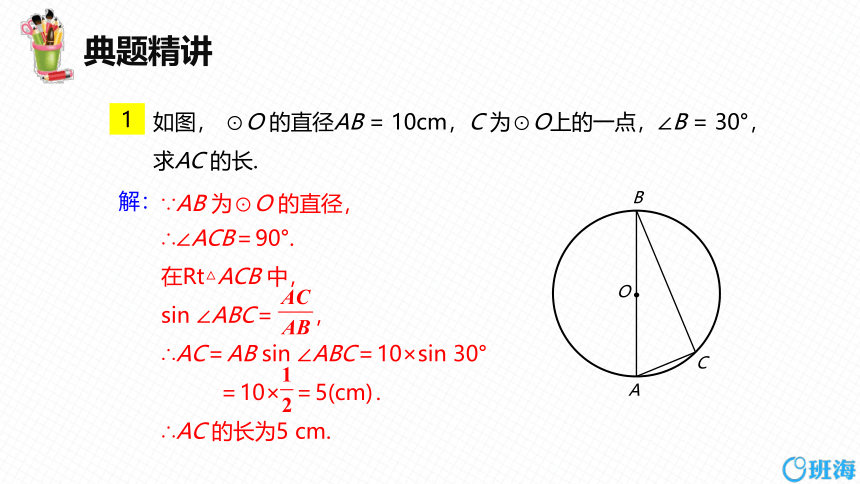
如图, ⊙O 的直径AB = 10cm,C 为⊙O上的一点,∠B = 30°,求AC 的长.
1
∵AB 为⊙O 的直径,
∴∠ACB=90°.
在Rt△ACB 中,
sin ∠ABC= ,
∴AC=AB sin ∠ABC=10×sin 30°
=10× =5(cm).
∴AC 的长为5 cm.
解:
.
O
C
A
B
典题精讲
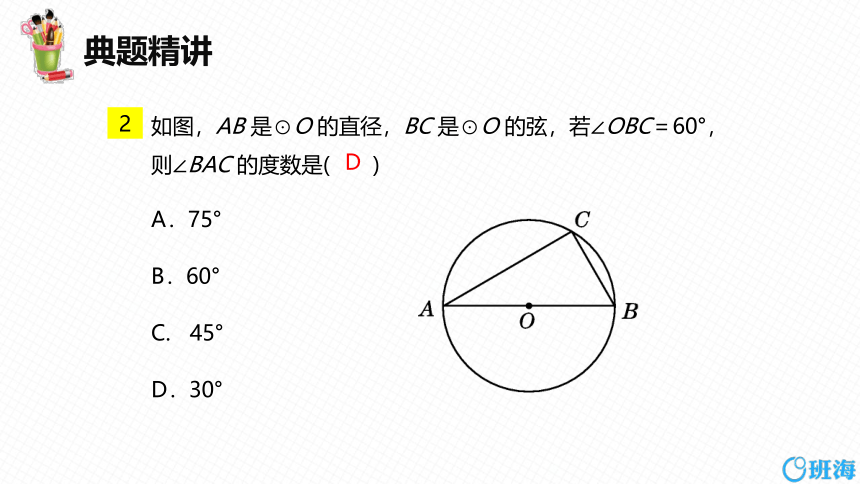
如图,AB 是⊙O 的直径,BC 是⊙O 的弦,若∠OBC=60°,则∠BAC 的度数是( )
A.75°
B.60°
C. 45°
D.30°
2
D
典题精讲
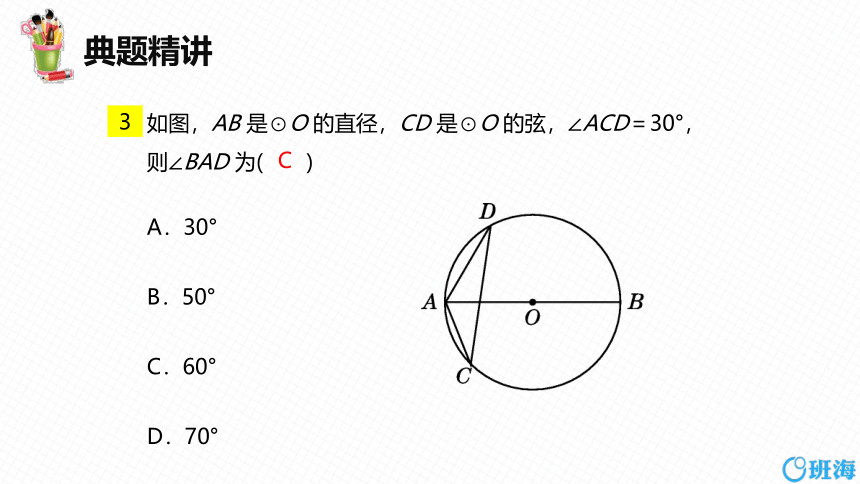
如图,AB 是⊙O 的直径,CD 是⊙O 的弦,∠ACD=30°,则∠BAD 为( )
A.30°
B.50°
C.60°
D.70°
3
C
典题精讲
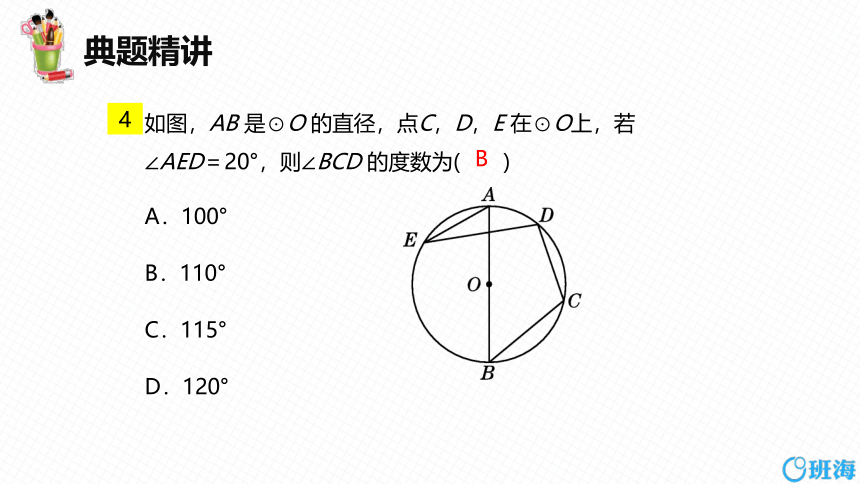
如图,AB 是⊙O 的直径,点C,D,E 在⊙O上,若∠AED=20°,则∠BCD 的度数为( )
A.100°
B.110°
C.115°
D.120°
4
B
典题精讲
如图,⊙O 的直径AB=4,BC 切⊙O 于点B,OC 平行于弦AD,OC=5,则AD 的长为( )
A.
B.
C.
D.
5
B
探索新知
2
知识点
直角所对的弦是直径
在如图中,圆周角∠A=90°,弦BC 是直径吗?为什么?
问 题
.
A
C
B
o
探索新知
归 纳
90°的圆周角所对的弦是直径.
探索新知
如图,已知经过原点的⊙P 与x 轴、y 轴分别交于A,B 两点,点C 是劣弧OB上一点,则∠ACB 等于( )
A.80° B.90° C.100° D.无法确定
例2
由∠AOB 与∠ACB 是优弧AB 所对的圆周角,根据圆周
角定理,即可求得∠ACB =∠AOB= 90°.
导引:
∵∠AOB 与∠ACB 是优弧AB 所对的圆周角,
∴∠AOB =∠ACB,
∵ ∠AOB = 90°,∴ ∠ACB = 90°.
解:
B
探索新知
总 结
此题考查了圆周角定理,此题比较简单,解题的关键是观察图形,得到∠AOB 与∠ACB 是优弧AB 所对的圆周角.
典题精讲
小明想用直角尺检査某些工件是否恰好为半圆形.
下面所示的四种圆弧形,你能判断哪个是半圆形?为什么
1
题图(2)是半圆形.
∵90°的圆周角所对的弦是直径.
解:
典题精讲
下列结论正确的是( )
A.直径所对的角是直角
B.90°的圆心角所对的弦是直径
C.同一条弦所对的圆周角相等
D.半圆所对的圆周角是直角
2
D
典题精讲
从下列直角三角尺与圆弧的位置关系中,可判断圆弧为半圆的是( )
3
B
典题精讲
如图,已知经过原点的⊙P 与x 轴,y 轴分别交于点A,B,C 是劣弧OB上一点,则∠ACB 等于( )
A.80°
B.90°
C.100°
D.无法确定
4
B
易错提醒
已知在半径为4的⊙O 中,弦AB=4 ,点P 在圆上,则∠APB=___________.
易错点:求圆周角的度数时容易考虑不周全
60°或120°
易错提醒
如图,当点P (P1)在弦AB 所对的优弧上时,过点O 作OC⊥AB 于点C,连接OA,OB.由垂径定理可得AC=2 ,∠AOC=∠BOC. 在Rt△OAC 中,OC=
=2= OA,所以∠OAC=30°.所以∠AOB=120°,所以∠AP1B=60°.同理当点P (P2)在弦AB 所对的劣弧上时,∠AP2B=120°.
易错提醒
对于“图形不明确型”问题,在解答时一般要进行分类讨论.一条弦(非直径)所对的圆周角有两种情况:顶点在优弧上的圆周角和顶点在劣弧上的圆周角,解题时要分情况求解,否则容易漏解.例如本题应分两种情况:点P 在弦AB 所对的优弧上和点P 在弦AB 所对的劣弧上.
易错总结:
学以致用
小试牛刀
如图,点P 在以AB 为直径的半圆内,连接AP,BP,并延长分别交半圆于点C,D,连接AD,BC 并延长交于点F,作直线PF,下列说法一定正确的是( )
①AC 垂直平分BF;②AC 平分∠BAF;③FP⊥AB;④BD⊥AF.
A.①③
B.①④
C.②④
D.③④
1
D
小试牛刀
如图,CD 是⊙O 的直径,CD=4,∠ACD=20°,点B 为弧AD 的中点,点P 是直径CD 上的一个动点,则PA+PB的最小值为________.
2
2
小试牛刀
3 如图,在△ABC 中,AB=AC,以AB 为直径的⊙O 分别交BC,AC 于点D,E,连接EB 交OD 于点F.
(1)求证:OD⊥BE;
(2)若DE= ,AB= ,求AE 的长.
小试牛刀
如图,连接AD.
∵AB 是⊙O 的直径,
∴∠ADB=∠AEB=90°.
∵AB=AC,
∴DC=DB.
∵OA=OB,∴OD∥AC.
∴∠OFB=∠AEB=90°,
∴OD⊥BE.
(1)证明:
小试牛刀
设AE=x,∵OD⊥BE,∴FE=FB,BD=ED.
∴BD=ED=
∵OF= AE= x,∴DF=OD-OF= - x.
在Rt△DFB 中,BF 2=DB 2-DF 2=
在Rt△OFB 中,BF 2=OB 2-OF 2=
∴
解得x= ,即AE= .
(2)解:
小试牛刀
4 如图,在△ABC 中,∠C=90°,D 是BC 边上一点,以DB 为直径的⊙O 经过AB 的中点E,交AD 的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sin B= ,EF= ,求CD 的长.
小试牛刀
如图,连接DE,
∵BD 是⊙O 的直径,
∴∠DEB=90°,
∵E 是AB 的中点,
∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
(1)证明:
小试牛刀
∵∠1=∠F,∴AE=EF=2
∴AB=2AE=4
在Rt△ABC 中,AC=AB sin B=4,
∴BC=
设CD=x,则AD=BD=8-x,
∵AC 2+CD 2=AD 2,
即42+x 2=(8-x )2,
∴x=3,即CD=3.
(2)解:
小试牛刀
5 如图,已知AB 是半径为1的⊙O 的直径,C 是圆上一点,D 是BC 的延长线上一点,过点D 的直线交AC 于E 点,交AB 于F 点,且△AEF 为等边三角形.
(1)求证:△DFB 是等腰三角形;
(2)若DA= AF,求证:CF⊥AB.
小试牛刀
(1)∵AB 是⊙O 的直径,
∴∠ACB=90°.
∵△AEF 为等边三角形,
∴∠CAB=∠EFA=60°.
∴∠B=90°-∠CAB=30°.
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°.
∴△DFB 是等腰三角形.
证明:
小试牛刀
(2)如图,过点A 作AM⊥DF 于点M,设AF=2a.
∵△AEF 是等边三角形,
∴FM=EM=a,AM= a,∠AEF=60°.
在Rt△DAM 中,AD= AF=2 a,
AM= a,
∴DM=
∴BF=DF=6a.
∴AB=AF+BF=8a.
小试牛刀
在Rt△ABC 中,∠B=30°,∠ACB=90°,
∴AC=4a.
∴CE=AC-AE=4a-2a=2a.
∴CE=EF.∴∠ECF=∠EFC.
∵∠AEF=∠ECF+∠EFC=60°,
∴∠CFE=30°.
∴∠AFC=∠AFE+∠EFC=60°+30°=90°.
∴CF⊥AB.
小试牛刀
6 如图,⊙C 经过原点且与两坐标轴分别交于点A (0,2)和点B (2 ,0).
(1)求线段AB 的长及∠ABO 的大小.
(2)在⊙C上是否存在一点P,使得△POB 是等腰三角形?若存在,请求出∠BOP 的度数;若不存在,请说明理由.
小试牛刀
(1)∵ A (0,2),B (2 ,0),
∴OA=2,OB=2
在Rt△AOB 中,AB=
如图,连接OC,∵∠AOB=90°,
∴AB 为⊙C 的直径,点C 为AB 的中点.
∴AC=OC= AB=2=OA.
∴△AOC 是等边三角形.
∴∠BAO=60°.∴∠ABO=30°.
解:
小试牛刀
(2)存在.如图,作OB 的垂直平分线MN,
交⊙C 于点M,N,交OB 于点D,连接OM,BM,ON,BN.
由垂径定理可得MN 必过点C,即MN 是⊙C 的直径.
∵MN 垂直平分OB,∴△OBM,△OBN 都是等腰三角形,
∴M,N 点均符合P 点的要求.
∵MN 是⊙C 的直径,∴∠MON=90°.
∵∠BMO=∠BAO=60°,
∴△OBM 是等边三角形.
∴∠BOM=60°.∴∠BON=30°.
故存在符合条件的P 点,∠BOP 的度数为60°或30°.
课堂小结
课堂小结
1.已知直径时,常添加辅助线构造直角三角形,即“见直径想直角”.题目中遇到直径时要考虑直径所对的圆周角为90°,遇到90°的圆周角时要考虑直角所对的弦为直径,这是圆中作辅助线的常用方法.
2.在解决圆的有关问题时,常常利用圆周角定理及其推论进行两种转化:一是利用同弧所对的圆周角相等,进行角与角之间的转化,二是将圆周角相等的问题转化为弦相等或弧相等的问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4 圆周角和圆心角的关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
1.什么叫做圆周角?
2.圆周角定理是什么?
3.圆周角定理的推论1的内容是什么?
新课精讲
探索新知
1
知识点
直径所对的圆周角是直角
直径所对的圆周角是多少度?请说明理由.
总结
直径所对的圆周角是直角.
探索新知
如图,AB 是⊙O 的直径,弦BC=BD,
若∠BOD=65°,求∠A 的度数.
要求∠A 的度数,可将其转化为求
所对的圆心角的度数,这样就需要连
接OC 这条辅助线了.
导引:
例1
如图,连接OC,∵BC=BD,
∴∠BOC=∠BOD=65°.
∴∠A= ∠BOC= ×65°=32.5°.
解:
探索新知
总 结
同圆或等圆中的弦、弧、圆心角、圆周角之间的关系可以互相转化,当某个结论不好求时,可运用转化思想将其转化为求与之相关的另一结论.
典题精讲
如图, ⊙O 的直径AB = 10cm,C 为⊙O上的一点,∠B = 30°,求AC 的长.
1
∵AB 为⊙O 的直径,
∴∠ACB=90°.
在Rt△ACB 中,
sin ∠ABC= ,
∴AC=AB sin ∠ABC=10×sin 30°
=10× =5(cm).
∴AC 的长为5 cm.
解:
.
O
C
A
B
典题精讲
如图,AB 是⊙O 的直径,BC 是⊙O 的弦,若∠OBC=60°,则∠BAC 的度数是( )
A.75°
B.60°
C. 45°
D.30°
2
D
典题精讲
如图,AB 是⊙O 的直径,CD 是⊙O 的弦,∠ACD=30°,则∠BAD 为( )
A.30°
B.50°
C.60°
D.70°
3
C
典题精讲
如图,AB 是⊙O 的直径,点C,D,E 在⊙O上,若∠AED=20°,则∠BCD 的度数为( )
A.100°
B.110°
C.115°
D.120°
4
B
典题精讲
如图,⊙O 的直径AB=4,BC 切⊙O 于点B,OC 平行于弦AD,OC=5,则AD 的长为( )
A.
B.
C.
D.
5
B
探索新知
2
知识点
直角所对的弦是直径
在如图中,圆周角∠A=90°,弦BC 是直径吗?为什么?
问 题
.
A
C
B
o
探索新知
归 纳
90°的圆周角所对的弦是直径.
探索新知
如图,已知经过原点的⊙P 与x 轴、y 轴分别交于A,B 两点,点C 是劣弧OB上一点,则∠ACB 等于( )
A.80° B.90° C.100° D.无法确定
例2
由∠AOB 与∠ACB 是优弧AB 所对的圆周角,根据圆周
角定理,即可求得∠ACB =∠AOB= 90°.
导引:
∵∠AOB 与∠ACB 是优弧AB 所对的圆周角,
∴∠AOB =∠ACB,
∵ ∠AOB = 90°,∴ ∠ACB = 90°.
解:
B
探索新知
总 结
此题考查了圆周角定理,此题比较简单,解题的关键是观察图形,得到∠AOB 与∠ACB 是优弧AB 所对的圆周角.
典题精讲
小明想用直角尺检査某些工件是否恰好为半圆形.
下面所示的四种圆弧形,你能判断哪个是半圆形?为什么
1
题图(2)是半圆形.
∵90°的圆周角所对的弦是直径.
解:
典题精讲
下列结论正确的是( )
A.直径所对的角是直角
B.90°的圆心角所对的弦是直径
C.同一条弦所对的圆周角相等
D.半圆所对的圆周角是直角
2
D
典题精讲
从下列直角三角尺与圆弧的位置关系中,可判断圆弧为半圆的是( )
3
B
典题精讲
如图,已知经过原点的⊙P 与x 轴,y 轴分别交于点A,B,C 是劣弧OB上一点,则∠ACB 等于( )
A.80°
B.90°
C.100°
D.无法确定
4
B
易错提醒
已知在半径为4的⊙O 中,弦AB=4 ,点P 在圆上,则∠APB=___________.
易错点:求圆周角的度数时容易考虑不周全
60°或120°
易错提醒
如图,当点P (P1)在弦AB 所对的优弧上时,过点O 作OC⊥AB 于点C,连接OA,OB.由垂径定理可得AC=2 ,∠AOC=∠BOC. 在Rt△OAC 中,OC=
=2= OA,所以∠OAC=30°.所以∠AOB=120°,所以∠AP1B=60°.同理当点P (P2)在弦AB 所对的劣弧上时,∠AP2B=120°.
易错提醒
对于“图形不明确型”问题,在解答时一般要进行分类讨论.一条弦(非直径)所对的圆周角有两种情况:顶点在优弧上的圆周角和顶点在劣弧上的圆周角,解题时要分情况求解,否则容易漏解.例如本题应分两种情况:点P 在弦AB 所对的优弧上和点P 在弦AB 所对的劣弧上.
易错总结:
学以致用
小试牛刀
如图,点P 在以AB 为直径的半圆内,连接AP,BP,并延长分别交半圆于点C,D,连接AD,BC 并延长交于点F,作直线PF,下列说法一定正确的是( )
①AC 垂直平分BF;②AC 平分∠BAF;③FP⊥AB;④BD⊥AF.
A.①③
B.①④
C.②④
D.③④
1
D
小试牛刀
如图,CD 是⊙O 的直径,CD=4,∠ACD=20°,点B 为弧AD 的中点,点P 是直径CD 上的一个动点,则PA+PB的最小值为________.
2
2
小试牛刀
3 如图,在△ABC 中,AB=AC,以AB 为直径的⊙O 分别交BC,AC 于点D,E,连接EB 交OD 于点F.
(1)求证:OD⊥BE;
(2)若DE= ,AB= ,求AE 的长.
小试牛刀
如图,连接AD.
∵AB 是⊙O 的直径,
∴∠ADB=∠AEB=90°.
∵AB=AC,
∴DC=DB.
∵OA=OB,∴OD∥AC.
∴∠OFB=∠AEB=90°,
∴OD⊥BE.
(1)证明:
小试牛刀
设AE=x,∵OD⊥BE,∴FE=FB,BD=ED.
∴BD=ED=
∵OF= AE= x,∴DF=OD-OF= - x.
在Rt△DFB 中,BF 2=DB 2-DF 2=
在Rt△OFB 中,BF 2=OB 2-OF 2=
∴
解得x= ,即AE= .
(2)解:
小试牛刀
4 如图,在△ABC 中,∠C=90°,D 是BC 边上一点,以DB 为直径的⊙O 经过AB 的中点E,交AD 的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sin B= ,EF= ,求CD 的长.
小试牛刀
如图,连接DE,
∵BD 是⊙O 的直径,
∴∠DEB=90°,
∵E 是AB 的中点,
∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
(1)证明:
小试牛刀
∵∠1=∠F,∴AE=EF=2
∴AB=2AE=4
在Rt△ABC 中,AC=AB sin B=4,
∴BC=
设CD=x,则AD=BD=8-x,
∵AC 2+CD 2=AD 2,
即42+x 2=(8-x )2,
∴x=3,即CD=3.
(2)解:
小试牛刀
5 如图,已知AB 是半径为1的⊙O 的直径,C 是圆上一点,D 是BC 的延长线上一点,过点D 的直线交AC 于E 点,交AB 于F 点,且△AEF 为等边三角形.
(1)求证:△DFB 是等腰三角形;
(2)若DA= AF,求证:CF⊥AB.
小试牛刀
(1)∵AB 是⊙O 的直径,
∴∠ACB=90°.
∵△AEF 为等边三角形,
∴∠CAB=∠EFA=60°.
∴∠B=90°-∠CAB=30°.
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°.
∴△DFB 是等腰三角形.
证明:
小试牛刀
(2)如图,过点A 作AM⊥DF 于点M,设AF=2a.
∵△AEF 是等边三角形,
∴FM=EM=a,AM= a,∠AEF=60°.
在Rt△DAM 中,AD= AF=2 a,
AM= a,
∴DM=
∴BF=DF=6a.
∴AB=AF+BF=8a.
小试牛刀
在Rt△ABC 中,∠B=30°,∠ACB=90°,
∴AC=4a.
∴CE=AC-AE=4a-2a=2a.
∴CE=EF.∴∠ECF=∠EFC.
∵∠AEF=∠ECF+∠EFC=60°,
∴∠CFE=30°.
∴∠AFC=∠AFE+∠EFC=60°+30°=90°.
∴CF⊥AB.
小试牛刀
6 如图,⊙C 经过原点且与两坐标轴分别交于点A (0,2)和点B (2 ,0).
(1)求线段AB 的长及∠ABO 的大小.
(2)在⊙C上是否存在一点P,使得△POB 是等腰三角形?若存在,请求出∠BOP 的度数;若不存在,请说明理由.
小试牛刀
(1)∵ A (0,2),B (2 ,0),
∴OA=2,OB=2
在Rt△AOB 中,AB=
如图,连接OC,∵∠AOB=90°,
∴AB 为⊙C 的直径,点C 为AB 的中点.
∴AC=OC= AB=2=OA.
∴△AOC 是等边三角形.
∴∠BAO=60°.∴∠ABO=30°.
解:
小试牛刀
(2)存在.如图,作OB 的垂直平分线MN,
交⊙C 于点M,N,交OB 于点D,连接OM,BM,ON,BN.
由垂径定理可得MN 必过点C,即MN 是⊙C 的直径.
∵MN 垂直平分OB,∴△OBM,△OBN 都是等腰三角形,
∴M,N 点均符合P 点的要求.
∵MN 是⊙C 的直径,∴∠MON=90°.
∵∠BMO=∠BAO=60°,
∴△OBM 是等边三角形.
∴∠BOM=60°.∴∠BON=30°.
故存在符合条件的P 点,∠BOP 的度数为60°或30°.
课堂小结
课堂小结
1.已知直径时,常添加辅助线构造直角三角形,即“见直径想直角”.题目中遇到直径时要考虑直径所对的圆周角为90°,遇到90°的圆周角时要考虑直角所对的弦为直径,这是圆中作辅助线的常用方法.
2.在解决圆的有关问题时,常常利用圆周角定理及其推论进行两种转化:一是利用同弧所对的圆周角相等,进行角与角之间的转化,二是将圆周角相等的问题转化为弦相等或弧相等的问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
