【班海精品】北师大版(新)九年级下-3.2圆的对称性【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-3.2圆的对称性【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览









文档简介
(共45张PPT)
2 圆的对称性
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
新课精讲
探索新知
1
知识点
圆的对称性
1.一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合,这就是圆的旋转不变性.
2.把圆绕圆心旋转180°,所得的图形与原图形重合,所以圆是中心对称图形,对称中心为圆心.
探索新知
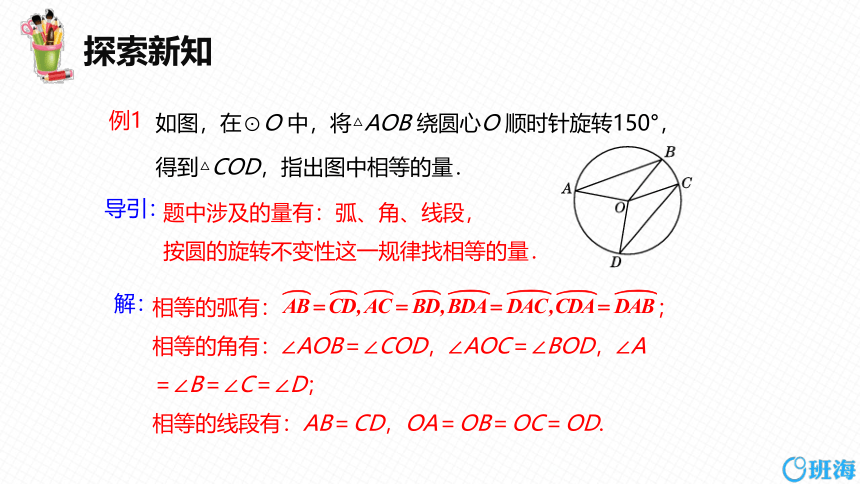
如图,在⊙O 中,将△AOB 绕圆心O 顺时针旋转150°,
得到△COD,指出图中相等的量.
例1
导引:
题中涉及的量有:弧、角、线段,
按圆的旋转不变性这一规律找相等的量.
相等的弧有: ;
相等的角有:∠AOB=∠COD,∠AOC=∠BOD,∠A
=∠B=∠C=∠D;
相等的线段有:AB=CD,OA=OB=OC=OD.
解:
探索新知
总 结
将一个图形绕一个定点旋转时, 具有下列特性:
一是旋转角度、方向相同,二是图形的形状、大小保持不变,因此本题圆中变换位置前后对应的弧、角、线段都相等.
典题精讲
日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
1
解:略.
下列图形:平行四边形、矩形、菱形、圆、等腰三角形,这些图形中只是轴对称图形的有( )
A.1个 B.2个
C.3个 D.4个
2
A
典题精讲
利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1) 是轴对称图形但不是中心对称图形;
(2) 是中心对称图形但不是轴对称图形;
(3) 既是轴对称图形又是中心对称图形.
3
解: (1)如图①②是轴对称图形但不是中心对称图形;
(2)如图③是中心对称图形但不是轴对称图形;
(3)如图④既是轴对称图形又是中心对称图形.
典题精讲
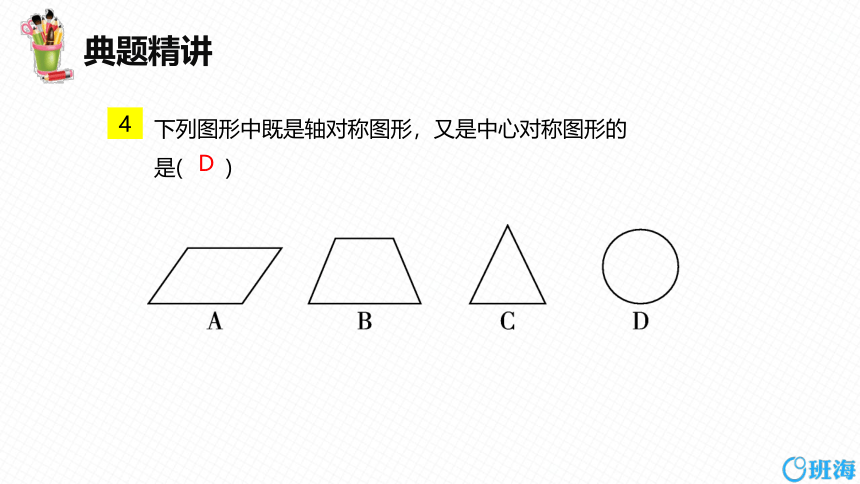
下列图形中既是轴对称图形,又是中心对称图形的是( )
4
D
探索新知
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?你是怎么想的?
在同圆或等圆中,如果两条弦相等,你能得出什么结论?
2
知识点
圆心角与所对的弧、弦之间的关系
探索新知
归 纳
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
探索新知
下列命题中,正确的是( )
①顶点在圆心的角是圆心角;
②相等的圆心角所对的弧也相等;
③在等圆中,圆心角不等,所对的弦也不等.
A.①和② B.②和③
C.①和③ D.①②③
例2
C
探索新知
导引:
①根据圆心角的定义知,顶点在圆心的角是圆心角,故正确;②缺少条件,必须是在同圆或等圆中,相等的圆心角所对的弧才相等,故错误;③根据弧、弦、圆心角之间的关系定理,可知在等圆中,若圆心角相等,则所对的弦相等,若圆心角不等,则所对的弦也不等,故正确.
探索新知
总 结
本题考查了对弧、弦、圆心角之间的关系的理解,对于圆中的一些易混易错结论应结合图形来解答.特别要注意:看是否有“在同圆或等圆中”这个前提条件.
典题精讲
下面四个图形中的角,是圆心角的是( )
1
D
典题精讲
如图,AB 为⊙O 的弦,∠A=40°,则AB 所对的圆心角等于( )
A.40°
B.80°
C.100°
D.120°
2
︵
C
典题精讲
如图,在△ABC 中,∠C=90°,∠A=25°,以点C 为圆心,BC为半径的圆交AB 于点D,交AC 于点E,则BD 的度数为( )
A.25°
B.30°
C.50°
D.65°
3
︵
C
典题精讲
如图,圆O 过五边形OABCD 的四个顶点.若AD=150°,∠A=65°,∠D=60°,则BC 的度数为何?( )
A.25°
B.40°
C.50°
D.55°
4
︵
︵
B
典题精讲
已知AB,CD 是⊙O 的直径,弦CE∥AB,∠COE=40°,则BD 的度数是( )
A.70° B.110°
C.40° D.70°或110°
5
︵
D
探索新知
3
知识点
相等的圆心角、弧、弦的对应关系
如图,将圆心角∠AOB 绕圆心O 旋转到∠A1OB1 的
位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
探索新知
如图,⊙O 与⊙O1是等圆,∠AOB =∠A1OB1=60°,请问上述结论还成立吗?为什么?
·
O
A
B
A1
·
O1
B1
·
探索新知
归 纳
弧、弦、圆心角之间的关系.
在同圆或等圆中:
(1)相等的圆心角所对的弧相等,所对的弦也相等.
(2)相等的弧所对的圆心角相等,所对的弦也相等.
(3)相等的弦所对的圆心角相等,所对的弧也相等.
探索新知
如图,AB,DE 是⊙O 的直径,C 是⊙O 上的一点,且
. BE 与CE 的大小有什么关系?为什么?
例3
解:
BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.
典题精讲
已知A,B 是⊙O上的两点,∠AOB= 120°,C 是AB 的中点. 试确定四边形OACB 的形状,并说明理由.
1
如图,四边形OACB 是菱形.理由如下:连接OC.
∵C 是AB 的中点,
∴AC=BC. ∴∠AOC=∠BOC.
∵∠AOB=120°,∴∠AOC=∠BOC=60°.
又∵OB=OC,OA=OC,
∴△BOC 和△AOC 都是等边三角形.
∴OB=BC=CA=AO. ∴四边形OACB 是菱形.
解:
︵
︵
︵
︵
典题精讲
如图,AB 是⊙O 的直径,若∠COA=∠DOB=60°,则与线段AO 的长度相等的线段有( )
A.3条
B.4条
C.5条
D.6条
2
D
典题精讲
在⊙O 中,圆心角∠AOB=2∠COD,则AB 与CD 的关系是( )
A. AB=2CD B. AB>2CD
C. AB<2CD D.不能确定
3
︵
︵
︵
︵
︵
︵
︵
︵
A
在⊙O 中,M,N 分别为弦AB,CD 的中点,如果OM=ON,那么在结论:①AB=CD;②AB=CD;③∠AOB=∠COD 中,正确的是( )
A.①② B.①③
C.②③ D.①②③
4
︵
︵
D
易错提醒
如图,在⊙O 中,弦AB>CD,OM⊥AB,ON⊥CD,M,N 分别为垂足,那么OM,ON 的大小关系是( )
A.OM>ON
B.OM=ON
C.OMD.无法确定
易错点:对圆中的有关线段的关系运用不当而致错
C
易错提醒
A或B
对于“在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都相等”这一性质中反映的各组量之间的关系判断不准,从而导致错误.
错解:
诊断:
学以致用
小试牛刀
如图,在⊙O 中,点C 是AB 的中点,∠A=50°,则∠BOC 等于( )
A.40°
B.45°
C.50°
D.60°
1
︵
A
小试牛刀
把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,则BC 的度数是( )
A.120°
B.135°
C.150°
D.165°
2
︵
C
小试牛刀
3 如图,AB 是⊙O 的直径,AC=CD,∠COD=60°.
(1)△AOC 是等边三角形吗?请说明理由.
(2)求证:OC∥BD.
小试牛刀
(1)△AOC 是等边三角形.理由如下:
∵AC=CD,∴∠AOC=∠COD=60°.
又∵OA=OC,∴△AOC 是等边三角形.
(2)证明:∵∠BOD=180°-∠AOC-∠COD
=180°-60°-60°=60°.
OB=OD,∴△OBD 为等边三角形.
∴∠D=60°.∴∠D=∠COD.
∴OC∥BD.
解:
小试牛刀
4 如图,在△AOB 中,AO=AB,以点O 为圆心,OB 为半径的圆交AB 于点D,交AO 于点E,AD=BO.
试证明BD=DE,并求∠A 的度数.
小试牛刀
设∠A=x °.∵AD=BO,OB=OD,∴OD=AD.
∴∠AOD=∠A=x °.
∴∠ABO=∠ODB=∠AOD+∠A=2x °.
∵AO=AB,∴∠AOB=∠ABO=2x °.
从而∠BOD=2x °-x °=x °,
即∠BOD=∠AOD.∴BD=DE.
在△BOD 中,由三角形的内角和为180°,
得2x+2x+x=180,
∴x=36,则∠A=36°.
解:
小试牛刀
5 如图,以 ABCD 的顶点A 为圆心,AB 为半径作圆,分别交AD,BC 于点E,F,延长BA 交⊙A于点G.
(1)求证:GE=EF;
(2)若BF 的度数为50°,求∠C 的度数.
小试牛刀
如图,连接AF,则AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD 是平行四边形,
∴AD∥BC.
∴∠EAF=∠AFB,∠GAE=∠ABF.
∴∠GAE=∠EAF.∴GE=EF.
∵BF 的度数为50°,
∴∠BAF=50°.∴∠ABF=∠AFB=65°.
又∵AB∥CD,∴∠ABF+∠C=180°.
∴∠C=180°-∠ABF=115°.
(1)证明:
(2)解:
小试牛刀
6 如图,已知AD 是⊙O 的直径,AB,AC 是弦,且AB=AC.
(1)求证:直径AD 平分∠BAC;
(2)若BC 经过半径OA 的中点E,点F 是CD 的中点,点G 是BF 的中点,⊙O 的半径为1.求GF 的长.
小试牛刀
如图,连接BD,CD.
∵AB=AC,∴AB=AC.
∵AD 是⊙O 的直径,
∴BD=CD.
∴BD=CD.
又∵AD=AD,
∴△ABD ≌ △ACD.
∴∠BAD=∠CAD.
∴直径AD 平分∠BAC.
(1)证明:
小试牛刀
如图,连接BO,CO,GO,FO.由(1)可知AD⊥BC,
又∵点E 是OA 的中点,∴BA=OB=AC=OC=OA.
∴∠BOA=∠AOC=60°.∵BD=CD,
∴∠BOD=∠COD=180°-∠AOC=120°.
又∵点F 是CD的中点,
∴∠COF=∠FOD= ∠COD=60°.
∴∠BOF=180°.∴BF 是⊙O 的直径.
又∵点G 是BF 的中点,∴∠FOG=90°.
∵⊙O 的半径是1,∴GF= OF=
(2)解:
课堂小结
课堂小结
1. 圆的中心对称性:圆是中心对称图形,具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2 圆的对称性
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
新课精讲
探索新知
1
知识点
圆的对称性
1.一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合,这就是圆的旋转不变性.
2.把圆绕圆心旋转180°,所得的图形与原图形重合,所以圆是中心对称图形,对称中心为圆心.
探索新知
如图,在⊙O 中,将△AOB 绕圆心O 顺时针旋转150°,
得到△COD,指出图中相等的量.
例1
导引:
题中涉及的量有:弧、角、线段,
按圆的旋转不变性这一规律找相等的量.
相等的弧有: ;
相等的角有:∠AOB=∠COD,∠AOC=∠BOD,∠A
=∠B=∠C=∠D;
相等的线段有:AB=CD,OA=OB=OC=OD.
解:
探索新知
总 结
将一个图形绕一个定点旋转时, 具有下列特性:
一是旋转角度、方向相同,二是图形的形状、大小保持不变,因此本题圆中变换位置前后对应的弧、角、线段都相等.
典题精讲
日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
1
解:略.
下列图形:平行四边形、矩形、菱形、圆、等腰三角形,这些图形中只是轴对称图形的有( )
A.1个 B.2个
C.3个 D.4个
2
A
典题精讲
利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1) 是轴对称图形但不是中心对称图形;
(2) 是中心对称图形但不是轴对称图形;
(3) 既是轴对称图形又是中心对称图形.
3
解: (1)如图①②是轴对称图形但不是中心对称图形;
(2)如图③是中心对称图形但不是轴对称图形;
(3)如图④既是轴对称图形又是中心对称图形.
典题精讲
下列图形中既是轴对称图形,又是中心对称图形的是( )
4
D
探索新知
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?你是怎么想的?
在同圆或等圆中,如果两条弦相等,你能得出什么结论?
2
知识点
圆心角与所对的弧、弦之间的关系
探索新知
归 纳
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
探索新知
下列命题中,正确的是( )
①顶点在圆心的角是圆心角;
②相等的圆心角所对的弧也相等;
③在等圆中,圆心角不等,所对的弦也不等.
A.①和② B.②和③
C.①和③ D.①②③
例2
C
探索新知
导引:
①根据圆心角的定义知,顶点在圆心的角是圆心角,故正确;②缺少条件,必须是在同圆或等圆中,相等的圆心角所对的弧才相等,故错误;③根据弧、弦、圆心角之间的关系定理,可知在等圆中,若圆心角相等,则所对的弦相等,若圆心角不等,则所对的弦也不等,故正确.
探索新知
总 结
本题考查了对弧、弦、圆心角之间的关系的理解,对于圆中的一些易混易错结论应结合图形来解答.特别要注意:看是否有“在同圆或等圆中”这个前提条件.
典题精讲
下面四个图形中的角,是圆心角的是( )
1
D
典题精讲
如图,AB 为⊙O 的弦,∠A=40°,则AB 所对的圆心角等于( )
A.40°
B.80°
C.100°
D.120°
2
︵
C
典题精讲
如图,在△ABC 中,∠C=90°,∠A=25°,以点C 为圆心,BC为半径的圆交AB 于点D,交AC 于点E,则BD 的度数为( )
A.25°
B.30°
C.50°
D.65°
3
︵
C
典题精讲
如图,圆O 过五边形OABCD 的四个顶点.若AD=150°,∠A=65°,∠D=60°,则BC 的度数为何?( )
A.25°
B.40°
C.50°
D.55°
4
︵
︵
B
典题精讲
已知AB,CD 是⊙O 的直径,弦CE∥AB,∠COE=40°,则BD 的度数是( )
A.70° B.110°
C.40° D.70°或110°
5
︵
D
探索新知
3
知识点
相等的圆心角、弧、弦的对应关系
如图,将圆心角∠AOB 绕圆心O 旋转到∠A1OB1 的
位置,你能发现哪些等量关系?为什么?
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,AB=A1B1 .
⌒
⌒
探索新知
如图,⊙O 与⊙O1是等圆,∠AOB =∠A1OB1=60°,请问上述结论还成立吗?为什么?
·
O
A
B
A1
·
O1
B1
·
探索新知
归 纳
弧、弦、圆心角之间的关系.
在同圆或等圆中:
(1)相等的圆心角所对的弧相等,所对的弦也相等.
(2)相等的弧所对的圆心角相等,所对的弦也相等.
(3)相等的弦所对的圆心角相等,所对的弧也相等.
探索新知
如图,AB,DE 是⊙O 的直径,C 是⊙O 上的一点,且
. BE 与CE 的大小有什么关系?为什么?
例3
解:
BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.
典题精讲
已知A,B 是⊙O上的两点,∠AOB= 120°,C 是AB 的中点. 试确定四边形OACB 的形状,并说明理由.
1
如图,四边形OACB 是菱形.理由如下:连接OC.
∵C 是AB 的中点,
∴AC=BC. ∴∠AOC=∠BOC.
∵∠AOB=120°,∴∠AOC=∠BOC=60°.
又∵OB=OC,OA=OC,
∴△BOC 和△AOC 都是等边三角形.
∴OB=BC=CA=AO. ∴四边形OACB 是菱形.
解:
︵
︵
︵
︵
典题精讲
如图,AB 是⊙O 的直径,若∠COA=∠DOB=60°,则与线段AO 的长度相等的线段有( )
A.3条
B.4条
C.5条
D.6条
2
D
典题精讲
在⊙O 中,圆心角∠AOB=2∠COD,则AB 与CD 的关系是( )
A. AB=2CD B. AB>2CD
C. AB<2CD D.不能确定
3
︵
︵
︵
︵
︵
︵
︵
︵
A
在⊙O 中,M,N 分别为弦AB,CD 的中点,如果OM=ON,那么在结论:①AB=CD;②AB=CD;③∠AOB=∠COD 中,正确的是( )
A.①② B.①③
C.②③ D.①②③
4
︵
︵
D
易错提醒
如图,在⊙O 中,弦AB>CD,OM⊥AB,ON⊥CD,M,N 分别为垂足,那么OM,ON 的大小关系是( )
A.OM>ON
B.OM=ON
C.OM
易错点:对圆中的有关线段的关系运用不当而致错
C
易错提醒
A或B
对于“在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都相等”这一性质中反映的各组量之间的关系判断不准,从而导致错误.
错解:
诊断:
学以致用
小试牛刀
如图,在⊙O 中,点C 是AB 的中点,∠A=50°,则∠BOC 等于( )
A.40°
B.45°
C.50°
D.60°
1
︵
A
小试牛刀
把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,则BC 的度数是( )
A.120°
B.135°
C.150°
D.165°
2
︵
C
小试牛刀
3 如图,AB 是⊙O 的直径,AC=CD,∠COD=60°.
(1)△AOC 是等边三角形吗?请说明理由.
(2)求证:OC∥BD.
小试牛刀
(1)△AOC 是等边三角形.理由如下:
∵AC=CD,∴∠AOC=∠COD=60°.
又∵OA=OC,∴△AOC 是等边三角形.
(2)证明:∵∠BOD=180°-∠AOC-∠COD
=180°-60°-60°=60°.
OB=OD,∴△OBD 为等边三角形.
∴∠D=60°.∴∠D=∠COD.
∴OC∥BD.
解:
小试牛刀
4 如图,在△AOB 中,AO=AB,以点O 为圆心,OB 为半径的圆交AB 于点D,交AO 于点E,AD=BO.
试证明BD=DE,并求∠A 的度数.
小试牛刀
设∠A=x °.∵AD=BO,OB=OD,∴OD=AD.
∴∠AOD=∠A=x °.
∴∠ABO=∠ODB=∠AOD+∠A=2x °.
∵AO=AB,∴∠AOB=∠ABO=2x °.
从而∠BOD=2x °-x °=x °,
即∠BOD=∠AOD.∴BD=DE.
在△BOD 中,由三角形的内角和为180°,
得2x+2x+x=180,
∴x=36,则∠A=36°.
解:
小试牛刀
5 如图,以 ABCD 的顶点A 为圆心,AB 为半径作圆,分别交AD,BC 于点E,F,延长BA 交⊙A于点G.
(1)求证:GE=EF;
(2)若BF 的度数为50°,求∠C 的度数.
小试牛刀
如图,连接AF,则AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD 是平行四边形,
∴AD∥BC.
∴∠EAF=∠AFB,∠GAE=∠ABF.
∴∠GAE=∠EAF.∴GE=EF.
∵BF 的度数为50°,
∴∠BAF=50°.∴∠ABF=∠AFB=65°.
又∵AB∥CD,∴∠ABF+∠C=180°.
∴∠C=180°-∠ABF=115°.
(1)证明:
(2)解:
小试牛刀
6 如图,已知AD 是⊙O 的直径,AB,AC 是弦,且AB=AC.
(1)求证:直径AD 平分∠BAC;
(2)若BC 经过半径OA 的中点E,点F 是CD 的中点,点G 是BF 的中点,⊙O 的半径为1.求GF 的长.
小试牛刀
如图,连接BD,CD.
∵AB=AC,∴AB=AC.
∵AD 是⊙O 的直径,
∴BD=CD.
∴BD=CD.
又∵AD=AD,
∴△ABD ≌ △ACD.
∴∠BAD=∠CAD.
∴直径AD 平分∠BAC.
(1)证明:
小试牛刀
如图,连接BO,CO,GO,FO.由(1)可知AD⊥BC,
又∵点E 是OA 的中点,∴BA=OB=AC=OC=OA.
∴∠BOA=∠AOC=60°.∵BD=CD,
∴∠BOD=∠COD=180°-∠AOC=120°.
又∵点F 是CD的中点,
∴∠COF=∠FOD= ∠COD=60°.
∴∠BOF=180°.∴BF 是⊙O 的直径.
又∵点G 是BF 的中点,∴∠FOG=90°.
∵⊙O 的半径是1,∴GF= OF=
(2)解:
课堂小结
课堂小结
1. 圆的中心对称性:圆是中心对称图形,具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量相等,那么它们所对应的其余各组量都分
别相等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
