【班海精品】北师大版(新)九年级下-3.4圆周角和圆心角的关系 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-3.4圆周角和圆心角的关系 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览










文档简介
(共45张PPT)
4 圆周角和圆心角的关系
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前边我学习了圆的内接三角形,圆的内接三角形有哪些性质呢?今天我们探究的圆的内接四边形的性质,我们根据圆内接三角形的定义,想一想如何给圆内接四边形下定义呢?
探索新知
1
知识点
圆内接多边形
圆内接多边形:
在圆内相异n 个点,按顺(或逆)时针的方向连接相邻的各点,可形成一个n 边形,此n 边形叫作此圆的圆内接多边形,此圆为多边形的外接圆.圆心为此n 边形的外心.外心到圆内接多边形各顶点的距离皆等长(即外接圆的半径)
探索新知
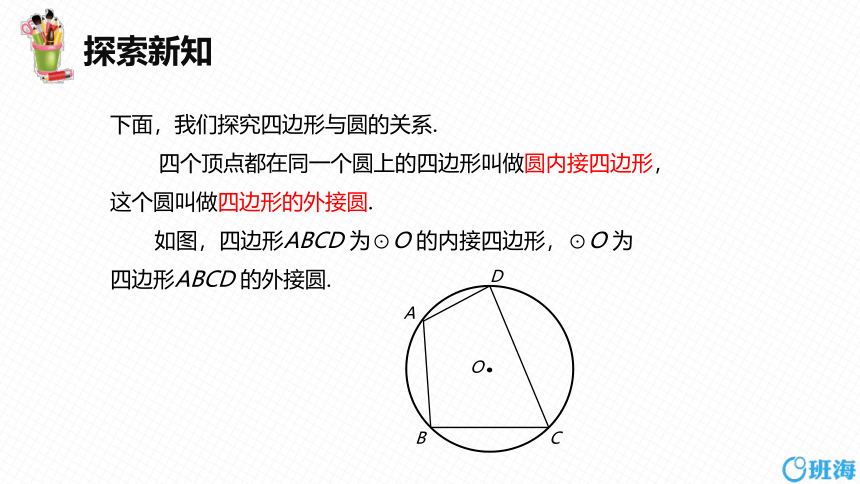
下面,我们探究四边形与圆的关系.
四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
如图,四边形ABCD 为⊙O 的内接四边形,⊙O 为四边形ABCD 的外接圆.
.
O
C
A
B
D
探索新知
四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
定义
探索新知
如果圆内接四边形ABCD 的对角线交点恰好是该圆的圆心,则四边形ABCD 一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
例1
分析:由圆内接四边形ABCD 的对角线交点恰好是该圆
的圆心,根据直径所对的圆周角是直角,可求得
四边形ABCD 的四个内角都是直角,即可判定四
边形ABCD 一定是矩形.
解:∵圆内接四边形ABCD 的对角线交点恰好是该圆的
圆心,∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD 一定是矩形. 故选B.
B
典题精讲
下列说法正确的是( )
A.在圆内部的多边形叫做圆内接多边形
B.过四边形的四个顶点的圆叫做这个四边形的外接圆
C.任意一个四边形都有外接圆
D.一个圆只有唯一一个内接四边形
1
B
典题精讲
下列多边形中一定有外接圆的是( )
A.三角形 B.四边形
C.五边形 D.六边形
2
A
下列命题中,不正确的是( )
A.矩形有一个外接圆
B.弦的垂直平分线一定平分弦所对的弧
C.菱形有一个外接圆
D.任何一个三角形都有一个外接圆
3
C
探索新知
2
知识点
圆内接四边形对角互补
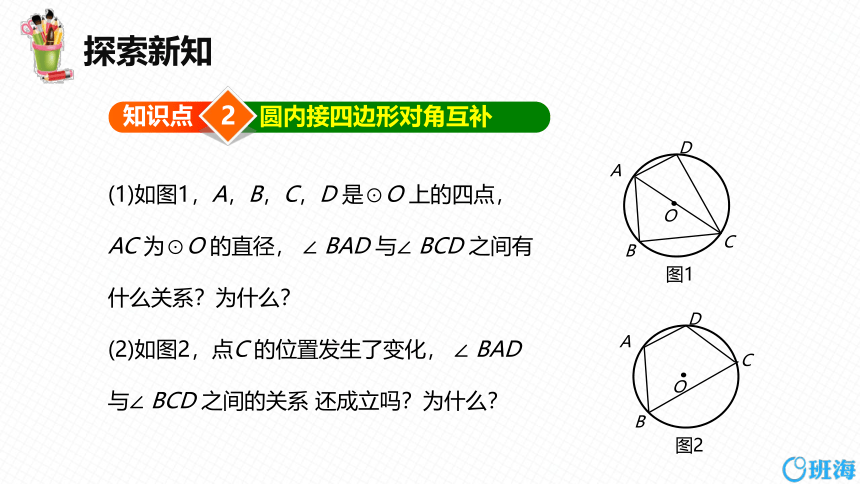
(1)如图1,A,B,C,D 是⊙O 上的四点,AC 为⊙O 的直径, ∠ BAD 与∠ BCD 之间有什么关系?为什么?
(2)如图2,点C 的位置发生了变化, ∠ BAD 与∠ BCD 之间的关系 还成立吗?为什么?
.
O
C
A
B
D
图1
.
O
C
A
B
D
图2
探索新知
归 纳
推论 圆内接四边形的对角互补.
探索新知
下面我们对它进行证明.
已知:如图,四边形ABCD 为⊙O 的内接四边形.
求证:∠BCD+∠BAD= 180°,
∠ABC+∠ADC= 180°.
.
O
C
A
B
D
探索新知
证明:如图,连接OB,OD.
∵ 与 所对的圆心角之和为360°,
∠BCD 和∠BAD 分别为 和 所对的
圆周角,
∴∠BCD+∠BAD= 180°.
同理可证,∠ABC+∠ADC=180°.
.
O
C
A
B
D
探索新知
如图,两圆相交于A,B 两点,小圆
经过大圆的圆心O,点C,D 分别在
两圆上,若∠ADB=100°,则
∠ACB 的度数为( )
A.35° B.40° C.50° D.80°
例2
要求∠ACB 的度数,即需要求出∠AOB 的度数(一条弧所对的
圆周角等于它所对的圆心角的一半),这样就产生辅助线AO,
BO,如图,连接AO,BO.在小圆中,∠AOB 是圆内接四边形
AOBD 中∠ADB 的对角,因此∠AOB=180°-∠ADB=
180°-100°=80°,所以∠ACB= ∠AOB=40°.
导引:
B
典题精讲
在圆内接四边形ABCD 中,对角∠A 与∠C 的度数之比是4:5,求∠C 的度数.
1
设∠A=4x °,则∠C=5x °.
∵∠A+∠C=180°,
∴4x °+5x °=180°.
∴x=20.
∴∠C=5×20°=100°
解:
典题精讲
在圆内接四边形ABCD 中,若∠A=70°,则∠C 等于( )
A.20° B.30° C.70° D.110°
下列命题:①圆内接平行四边形是矩形;②圆内接矩形是正方形;③圆内接菱形是正方形;④任意四边形一定有外接圆.其中真命题有( )
A.1个 B.2个 C.3个 D.4个
2
3
D
B
典题精讲
如图,四边形ABCD 内接于⊙O,若四边形ABCO 是平行四边形,则∠ADC 的大小为( )
A.45°
B.50°
C.60°
D.75°
4
C
典题精讲
如图,两圆相交于A,B 两点,小圆经过大圆圆心O,点C,D 分别在两圆上,若∠ADB=100°,则∠ACB 的度数为( )
A.35°
B.40°
C.50°
D.80°
5
B
探索新知
3
知识点
圆内接四边形的外角等于其内对角
想一想
如图, ∠DCE 是圆内接四边形ABCD 的一个外角,
∠A 与∠DCE 的大小有什么关系?
.
O
C
A
B
D
E
推论:圆内接四边形的一个外角等于它的内对角.
探索新知
已知:如图,两个等圆⊙O1和⊙O2相交于A,B 两点,
经过点A 的直线与两圆分别交于点C,点D,经过点B
的直线与两圆分别交于点E,点F. 若CD∥EF,求证:
(1)四边形CEFD 是平行四边形;
(2) .
例3
探索新知
(1)已知CD∥EF,需证CE∥DF;连接AB,由圆内接
四边形的性质,知:∠BAD=∠E,∠BAD+∠F=
180°,可得∠E+∠F=180°,进而可得CE∥DF,
由此得证.(2)由四边形CEFD 是平行四边形,得CE=
DF.由于⊙O1和⊙O2是两个等圆,因此 .
导引:
探索新知
解:
(1)连接AB,如图.
∵四边形ABEC 是⊙O1的内接四边形,∴∠BAD=∠E.
又∵四边形ADFB 是⊙O2的内接四边形,
∴∠BAD+∠F=180°.∴∠E+∠F=180°.∴CE∥DF.
又∵CD∥EF,
∴四边形CEFD 是平行四边形.
(2)由(1)得:四边形CEFD 是平行四边形,∴CE=DF.
又∵⊙O1和⊙O2是两个等圆,
∴ .
探索新知
总 结
连接两圆共同的弦(如本题中连接AB )是解答这类问题的重要辅助线,它将两圆的有关角联系在一起,起到一种桥梁作用.
典题精讲
如图,四边形ABCD 是圆内接四边形,E 是BC 延长线上一点,若∠BAD=105°,则∠DCE=________.
1
105°
典题精讲
如图,四边形ABCD 内接于⊙O,DA=DC,∠CBE=50°,则∠DAC 的大小为( )
A.130°
B.100°
C.65°
D.50°
2
C
典题精讲
如图,四边形ABCD 为⊙O 的内接四边形,E 为AB 延长线上一点,∠CBE=40°,则∠AOC 等于( )
A.20°
B.40°
C.80°
D.100°
3
C
典题精讲
如图,四边形ABCD 为⊙O 的内接四边形,延长AB 与DC 相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC 的度数为( )
A.50°
B.60°
C.80°
D.85°
4
C
易错提醒
已知△ABC 内接于⊙O,OD⊥AC 于点D,如果∠COD=32°,那么∠B 的度数为( )
A.16° B.32°
C.16°或164° D.32°或148°
易错点:画图时考虑不全而漏解
D
学以致用
小试牛刀
如图,⊙O 的半径是2,AB 是⊙O 的弦,点P 是弦AB上的动点,且1≤OP≤2,则弦AB 所对的圆周角的度数是( )
A.60°
B.120°
C.60°或120°
D.30°或150°
1
C
小试牛刀
如图,已知⊙O 为四边形ABCD 的外接圆,O 为圆心,若∠BCD=120°,AB=AD=2,则⊙O 的半径长为( )
A.
B.
C.
D.
2
D
小试牛刀
3 如图,⊙C 过原点,且与两坐标轴分别交于点A,B,点A 的坐标为(0,3),M 是第三象限内OB 上一点,∠BMO=120°,求⊙C 的半径及点B 的坐标.
小试牛刀
由题意知四边形AOMB 为⊙C 的内接四边形,
∴∠BAO=180°-∠BMO=180°-120°=60°.
∴∠ABO=90°-∠BAO=90°-60°=30°.
在Rt△ABO 中,易知OA=3,得AB=2OA=6.
∴AC=BC=3,OB=
∴⊙C 的半径为3,点B 的坐标是(-3 ,0).
解:
小试牛刀
4 如图,四边形ABCD 内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°.求证:
(1)AD=CD;
(2)AB 是⊙O 的直径.
小试牛刀
(1)四边形ABCD 内接于⊙O,
∴∠ADC=180°-∠B=130°.
∵∠ACD=25°,
∴∠DAC=180°-∠ADC-∠ACD
=180°-130°-25°=25°.
∴∠DAC=∠ACD.∴AD=CD.
(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,
∠B=50°,∴∠ACB=180°-∠B-∠BAC
=180°-50°-40°=90°.
∴AB 是⊙O 的直径.
证明:
小试牛刀
5 如图,四边形ABCD 是⊙O 的内接四边形,BC 的延长线与AD 的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD 于点F,OE⊥CD,求证:△ABE 是等边三角形.
小试牛刀
(1)∵四边形ABCD 是⊙O 的内接四边形,
∴∠A=∠DCE.
∵DC=DE,∴∠DCE=∠AEB.
∴∠A=∠AEB.
证明:
小试牛刀
(2)∵∠A=∠AEB,
∴△ABE 是等腰三角形.
∵OE⊥CD,∴CF=DF.
∴OE 是CD 的垂直平分线.
∴ED=EC.
又∵DC=DE,∴DC=DE=EC.
∴△DCE 是等边三角形.
∴∠AEB=60°,
∴△ABE 是等边三角形.
小试牛刀
6 如图,已知四边形ABCD 内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O 的半径为3,求BC 的长.
小试牛刀
∵四边形ABCD 内接于圆O,
∴∠DCB+∠BAD=180°.
∵∠BAD=105°,
∴∠DCB=180°-105°=75°.
∴∠DCB=∠DBC=75°.
∴BD=CD.
(1)证明:
小试牛刀
∵∠DCB=∠DBC=75°,
∴∠BDC=30°.如图,连接OB,OC,
由圆周角定理,得∠BOC=60°.
∴BC 的长等于圆O 的周长的
∴BC的长为 ×2π×3=π.
(2)解:
课堂小结
课堂小结
圆内接四边形的角的“两种关系”:
(1)对角互补,若四边形ABCD 为⊙O 的内接四边形,
则∠A+∠C=180°,∠B+∠D=180°.
(2)任一外角与其相邻的内角的对角相等,简称圆内
接四边形的外角等于其内对角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4 圆周角和圆心角的关系
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前边我学习了圆的内接三角形,圆的内接三角形有哪些性质呢?今天我们探究的圆的内接四边形的性质,我们根据圆内接三角形的定义,想一想如何给圆内接四边形下定义呢?
探索新知
1
知识点
圆内接多边形
圆内接多边形:
在圆内相异n 个点,按顺(或逆)时针的方向连接相邻的各点,可形成一个n 边形,此n 边形叫作此圆的圆内接多边形,此圆为多边形的外接圆.圆心为此n 边形的外心.外心到圆内接多边形各顶点的距离皆等长(即外接圆的半径)
探索新知
下面,我们探究四边形与圆的关系.
四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
如图,四边形ABCD 为⊙O 的内接四边形,⊙O 为四边形ABCD 的外接圆.
.
O
C
A
B
D
探索新知
四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
定义
探索新知
如果圆内接四边形ABCD 的对角线交点恰好是该圆的圆心,则四边形ABCD 一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
例1
分析:由圆内接四边形ABCD 的对角线交点恰好是该圆
的圆心,根据直径所对的圆周角是直角,可求得
四边形ABCD 的四个内角都是直角,即可判定四
边形ABCD 一定是矩形.
解:∵圆内接四边形ABCD 的对角线交点恰好是该圆的
圆心,∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD 一定是矩形. 故选B.
B
典题精讲
下列说法正确的是( )
A.在圆内部的多边形叫做圆内接多边形
B.过四边形的四个顶点的圆叫做这个四边形的外接圆
C.任意一个四边形都有外接圆
D.一个圆只有唯一一个内接四边形
1
B
典题精讲
下列多边形中一定有外接圆的是( )
A.三角形 B.四边形
C.五边形 D.六边形
2
A
下列命题中,不正确的是( )
A.矩形有一个外接圆
B.弦的垂直平分线一定平分弦所对的弧
C.菱形有一个外接圆
D.任何一个三角形都有一个外接圆
3
C
探索新知
2
知识点
圆内接四边形对角互补
(1)如图1,A,B,C,D 是⊙O 上的四点,AC 为⊙O 的直径, ∠ BAD 与∠ BCD 之间有什么关系?为什么?
(2)如图2,点C 的位置发生了变化, ∠ BAD 与∠ BCD 之间的关系 还成立吗?为什么?
.
O
C
A
B
D
图1
.
O
C
A
B
D
图2
探索新知
归 纳
推论 圆内接四边形的对角互补.
探索新知
下面我们对它进行证明.
已知:如图,四边形ABCD 为⊙O 的内接四边形.
求证:∠BCD+∠BAD= 180°,
∠ABC+∠ADC= 180°.
.
O
C
A
B
D
探索新知
证明:如图,连接OB,OD.
∵ 与 所对的圆心角之和为360°,
∠BCD 和∠BAD 分别为 和 所对的
圆周角,
∴∠BCD+∠BAD= 180°.
同理可证,∠ABC+∠ADC=180°.
.
O
C
A
B
D
探索新知
如图,两圆相交于A,B 两点,小圆
经过大圆的圆心O,点C,D 分别在
两圆上,若∠ADB=100°,则
∠ACB 的度数为( )
A.35° B.40° C.50° D.80°
例2
要求∠ACB 的度数,即需要求出∠AOB 的度数(一条弧所对的
圆周角等于它所对的圆心角的一半),这样就产生辅助线AO,
BO,如图,连接AO,BO.在小圆中,∠AOB 是圆内接四边形
AOBD 中∠ADB 的对角,因此∠AOB=180°-∠ADB=
180°-100°=80°,所以∠ACB= ∠AOB=40°.
导引:
B
典题精讲
在圆内接四边形ABCD 中,对角∠A 与∠C 的度数之比是4:5,求∠C 的度数.
1
设∠A=4x °,则∠C=5x °.
∵∠A+∠C=180°,
∴4x °+5x °=180°.
∴x=20.
∴∠C=5×20°=100°
解:
典题精讲
在圆内接四边形ABCD 中,若∠A=70°,则∠C 等于( )
A.20° B.30° C.70° D.110°
下列命题:①圆内接平行四边形是矩形;②圆内接矩形是正方形;③圆内接菱形是正方形;④任意四边形一定有外接圆.其中真命题有( )
A.1个 B.2个 C.3个 D.4个
2
3
D
B
典题精讲
如图,四边形ABCD 内接于⊙O,若四边形ABCO 是平行四边形,则∠ADC 的大小为( )
A.45°
B.50°
C.60°
D.75°
4
C
典题精讲
如图,两圆相交于A,B 两点,小圆经过大圆圆心O,点C,D 分别在两圆上,若∠ADB=100°,则∠ACB 的度数为( )
A.35°
B.40°
C.50°
D.80°
5
B
探索新知
3
知识点
圆内接四边形的外角等于其内对角
想一想
如图, ∠DCE 是圆内接四边形ABCD 的一个外角,
∠A 与∠DCE 的大小有什么关系?
.
O
C
A
B
D
E
推论:圆内接四边形的一个外角等于它的内对角.
探索新知
已知:如图,两个等圆⊙O1和⊙O2相交于A,B 两点,
经过点A 的直线与两圆分别交于点C,点D,经过点B
的直线与两圆分别交于点E,点F. 若CD∥EF,求证:
(1)四边形CEFD 是平行四边形;
(2) .
例3
探索新知
(1)已知CD∥EF,需证CE∥DF;连接AB,由圆内接
四边形的性质,知:∠BAD=∠E,∠BAD+∠F=
180°,可得∠E+∠F=180°,进而可得CE∥DF,
由此得证.(2)由四边形CEFD 是平行四边形,得CE=
DF.由于⊙O1和⊙O2是两个等圆,因此 .
导引:
探索新知
解:
(1)连接AB,如图.
∵四边形ABEC 是⊙O1的内接四边形,∴∠BAD=∠E.
又∵四边形ADFB 是⊙O2的内接四边形,
∴∠BAD+∠F=180°.∴∠E+∠F=180°.∴CE∥DF.
又∵CD∥EF,
∴四边形CEFD 是平行四边形.
(2)由(1)得:四边形CEFD 是平行四边形,∴CE=DF.
又∵⊙O1和⊙O2是两个等圆,
∴ .
探索新知
总 结
连接两圆共同的弦(如本题中连接AB )是解答这类问题的重要辅助线,它将两圆的有关角联系在一起,起到一种桥梁作用.
典题精讲
如图,四边形ABCD 是圆内接四边形,E 是BC 延长线上一点,若∠BAD=105°,则∠DCE=________.
1
105°
典题精讲
如图,四边形ABCD 内接于⊙O,DA=DC,∠CBE=50°,则∠DAC 的大小为( )
A.130°
B.100°
C.65°
D.50°
2
C
典题精讲
如图,四边形ABCD 为⊙O 的内接四边形,E 为AB 延长线上一点,∠CBE=40°,则∠AOC 等于( )
A.20°
B.40°
C.80°
D.100°
3
C
典题精讲
如图,四边形ABCD 为⊙O 的内接四边形,延长AB 与DC 相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC 的度数为( )
A.50°
B.60°
C.80°
D.85°
4
C
易错提醒
已知△ABC 内接于⊙O,OD⊥AC 于点D,如果∠COD=32°,那么∠B 的度数为( )
A.16° B.32°
C.16°或164° D.32°或148°
易错点:画图时考虑不全而漏解
D
学以致用
小试牛刀
如图,⊙O 的半径是2,AB 是⊙O 的弦,点P 是弦AB上的动点,且1≤OP≤2,则弦AB 所对的圆周角的度数是( )
A.60°
B.120°
C.60°或120°
D.30°或150°
1
C
小试牛刀
如图,已知⊙O 为四边形ABCD 的外接圆,O 为圆心,若∠BCD=120°,AB=AD=2,则⊙O 的半径长为( )
A.
B.
C.
D.
2
D
小试牛刀
3 如图,⊙C 过原点,且与两坐标轴分别交于点A,B,点A 的坐标为(0,3),M 是第三象限内OB 上一点,∠BMO=120°,求⊙C 的半径及点B 的坐标.
小试牛刀
由题意知四边形AOMB 为⊙C 的内接四边形,
∴∠BAO=180°-∠BMO=180°-120°=60°.
∴∠ABO=90°-∠BAO=90°-60°=30°.
在Rt△ABO 中,易知OA=3,得AB=2OA=6.
∴AC=BC=3,OB=
∴⊙C 的半径为3,点B 的坐标是(-3 ,0).
解:
小试牛刀
4 如图,四边形ABCD 内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°.求证:
(1)AD=CD;
(2)AB 是⊙O 的直径.
小试牛刀
(1)四边形ABCD 内接于⊙O,
∴∠ADC=180°-∠B=130°.
∵∠ACD=25°,
∴∠DAC=180°-∠ADC-∠ACD
=180°-130°-25°=25°.
∴∠DAC=∠ACD.∴AD=CD.
(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,
∠B=50°,∴∠ACB=180°-∠B-∠BAC
=180°-50°-40°=90°.
∴AB 是⊙O 的直径.
证明:
小试牛刀
5 如图,四边形ABCD 是⊙O 的内接四边形,BC 的延长线与AD 的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD 于点F,OE⊥CD,求证:△ABE 是等边三角形.
小试牛刀
(1)∵四边形ABCD 是⊙O 的内接四边形,
∴∠A=∠DCE.
∵DC=DE,∴∠DCE=∠AEB.
∴∠A=∠AEB.
证明:
小试牛刀
(2)∵∠A=∠AEB,
∴△ABE 是等腰三角形.
∵OE⊥CD,∴CF=DF.
∴OE 是CD 的垂直平分线.
∴ED=EC.
又∵DC=DE,∴DC=DE=EC.
∴△DCE 是等边三角形.
∴∠AEB=60°,
∴△ABE 是等边三角形.
小试牛刀
6 如图,已知四边形ABCD 内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O 的半径为3,求BC 的长.
小试牛刀
∵四边形ABCD 内接于圆O,
∴∠DCB+∠BAD=180°.
∵∠BAD=105°,
∴∠DCB=180°-105°=75°.
∴∠DCB=∠DBC=75°.
∴BD=CD.
(1)证明:
小试牛刀
∵∠DCB=∠DBC=75°,
∴∠BDC=30°.如图,连接OB,OC,
由圆周角定理,得∠BOC=60°.
∴BC 的长等于圆O 的周长的
∴BC的长为 ×2π×3=π.
(2)解:
课堂小结
课堂小结
圆内接四边形的角的“两种关系”:
(1)对角互补,若四边形ABCD 为⊙O 的内接四边形,
则∠A+∠C=180°,∠B+∠D=180°.
(2)任一外角与其相邻的内角的对角相等,简称圆内
接四边形的外角等于其内对角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
