【班海精品】北师大版(新)九年级下-3.5确定圆的条件【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-3.5确定圆的条件【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览






文档简介
(共51张PPT)
5 确定圆的条件
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、过一点可以作几条直线?
2、过几点可确定一条直线?
过几点可以确定一个圆呢?
新课精讲
探索新知
1
知识点
确定圆的条件
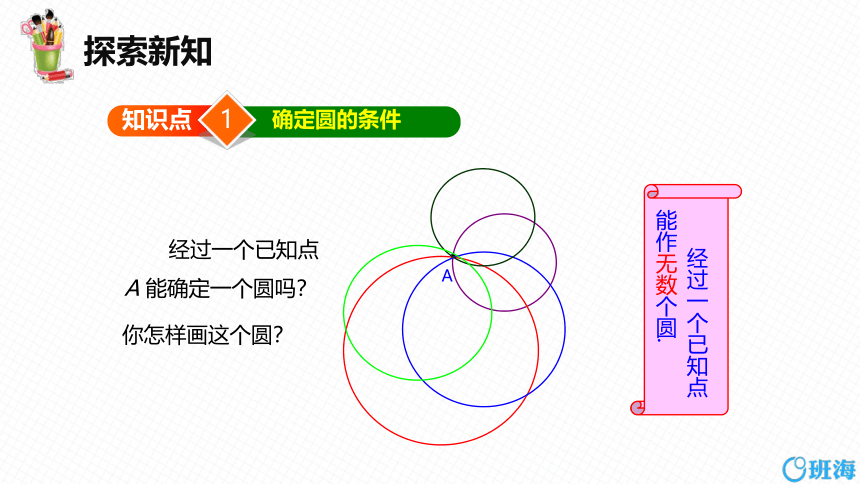
经过一个已知点A 能确定一个圆吗?
A
经过一个已知点能作无数个圆.
你怎样画这个圆?
探索新知
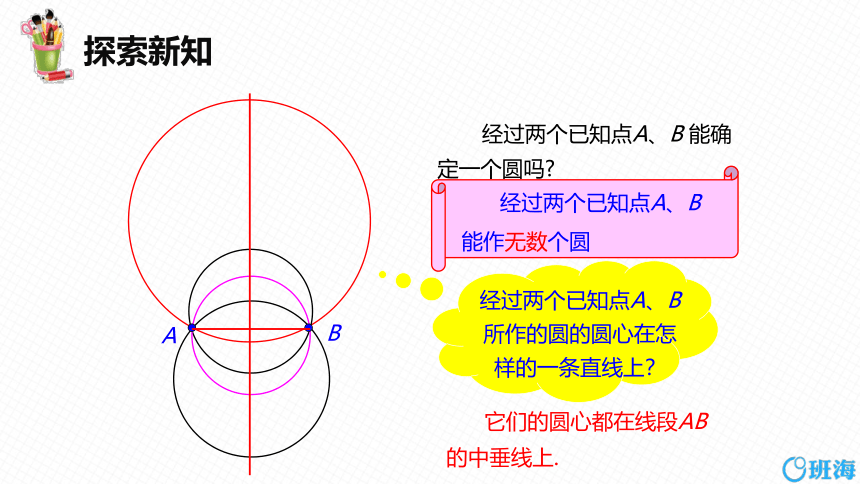
经过两个已知点A、B 能确
定一个圆吗
A
B
它们的圆心都在线段AB 的中垂线上.
经过两个已知点A、B
所作的圆的圆心在怎
样的一条直线上?
经过两个已知点A、B 能作无数个圆
探索新知
A
B
C
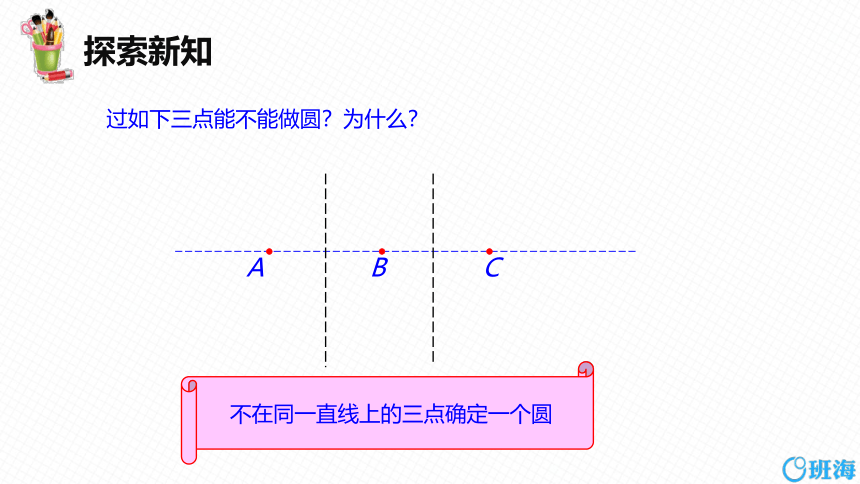
过如下三点能不能做圆?为什么?
不在同一直线上的三点确定一个圆
探索新知
如图①是一个残破的圆轮,李师傅想要再浇铸一个
同样大小的圆轮,你能想办法帮助李师傅吗?
例1
导引:
可先在圆弧上任意取三个点,然后作出两条弦,分别作
这两条弦的垂直平分线即可确定圆轮所在圆的圆心.
探索新知
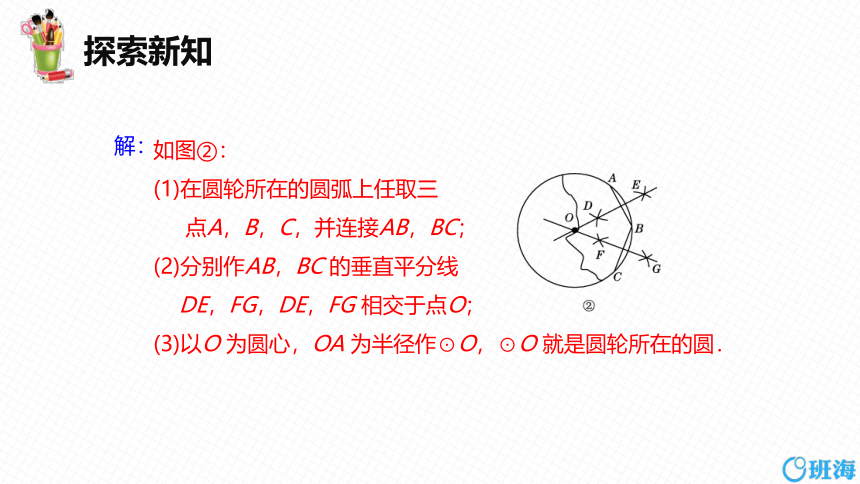
解:
如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC 的垂直平分线
DE,FG,DE,FG 相交于点O;
(3)以O 为圆心,OA 为半径作⊙O,⊙O 就是圆轮所在的圆.
探索新知
总 结
经过不在同一条直线上的三点A,B,C 作圆,圆心O 是线段AB,BC 的垂直平分线的交点,再以OA (或OB,OC )为半径作圆即可,这样的圆只能作一个.
典题精讲
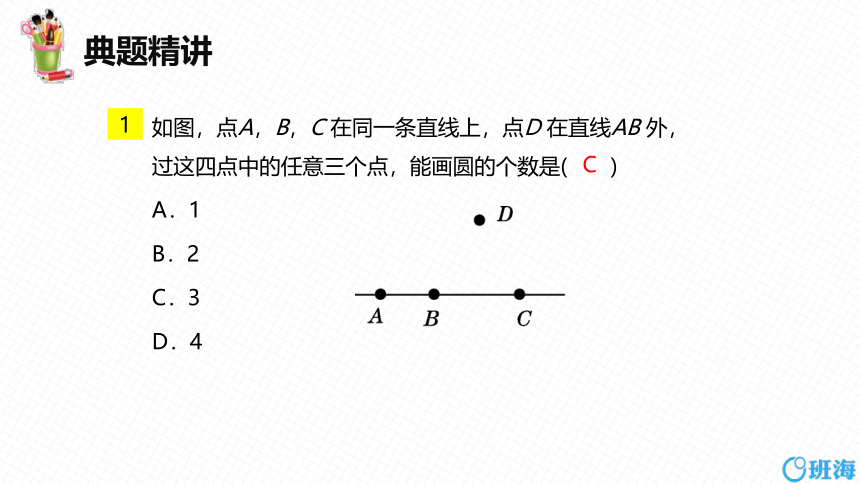
如图,点A,B,C 在同一条直线上,点D 在直线AB 外,过这四点中的任意三个点,能画圆的个数是( )
A.1
B.2
C.3
D.4
1
C
典题精讲
已知AB=4 cm,则过点A,B 且半径为3 cm的圆有( )
A.1个 B.2个
C.3个 D.4个
2
B
下列说法中正确的是( )
A.两个点确定一个圆
B.三个点确定一个圆
C.四个点确定一个圆
D.不共线的三个点确定一个圆
3
C
典题精讲
如图,在5×5的正方形网格中,一条圆弧经过A,B,C 三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
4
B
探索新知
2
知识点
三角形的外接圆、外心
已知△ABC,用直尺和圆规作出过点A、B、C 的圆.
A
B
C
O
探索新知
定 义
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
探索新知
如图:⊙O 是△ABC 的外接圆, △ABC 是⊙O 的内接三角形,点O 是△ABC 的外心.
外心是△ABC 三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
探索新知
三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一点的距离为半径作圆即可.
探索新知
如图,在平面直角坐标系中,点A,B,C 的坐标分别为(1,4),(5,4),(1,-2),则△ABC 外接圆的圆心坐标是( )
A.(2,3)
B.(3,2)
C.(1,3)
D.(3,1)
例2
D
探索新知
导引:
由A (1,4),B (5,4)可知AB∥x 轴,△ABC 的外接圆
圆心在线段AB 的垂直平分线上,所以圆心的横坐标
应为 =3;同理,圆心还应在线段AC 的垂直平
分线上,其纵坐标应为 =1.
探索新知
总 结
根据垂径定理的推论“弦的垂直平分线必过圆心”,作两条弦的垂直平分线,交点即为圆心.
探索新知
如图1,△ABC 内接于⊙O,∠C=45°,AB=4,求⊙O 的半径.
例3
图1
探索新知
导引:
要求⊙O 的半径,已知弦AB 的长,需以AB 为边与
⊙O 的半径(或直径)构成等腰直角三角形,因此有
两个切入点.方法一:如图2,连接OA,OB,利
用圆周角定理可得∠AOB=2∠C=90°,再利用
勾股定理求出半径;方法二:
如图2,作直径AD,连接BD,
利用同弧所对的圆周角相等,得
∠D=∠C=45°,再利用勾股
定理可求出半径.
图2
探索新知
解:
方法一:如图1,连接OA,OB,设⊙O 的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB 2=AB 2,即r 2+r 2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O 的半径为2 .
图1
探索新知
方法二:如图2,作直径AD,连接BD,设⊙O 的半径为r.
∵AD 为⊙O 的直径,
∴∠ABD=90°.
又∵∠D=∠C=45°,∴∠DAB=45°.
∴BD=AB=4.
在Rt△ABD 中,AB 2+BD 2=AD 2,即42+42=(2r )2
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O 的半径为2 .
图2
探索新知
总 结
求三角形的外接圆半径时,最常用的办法是作出圆心与三角形顶点的连线(即半径),延长使这条半径变为直径,将求半径转化为直角三角形中求边的长.
典题精讲
已知下面的三个三角形,分别作出它们的外接圆. 它们外心的位置有怎样的特点?
1
解:作图略.经观察发现:锐角三角形的外心在三角形的内部;
直角三角形的外心在斜边的中点处;钝角三角形的外心在三
角形的外部.
典题精讲
下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;
② 任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内;
④三角形的外心到三角形三边的距离相等;
⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4
2
B
典题精讲
如图,AC,BE 是⊙O 的直径,弦AD 与BE 交于点F,下列三角形中,外心不是点O 的是( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE
3
B
典题精讲
如图,在平面直角坐标系xOy 中,点A 的坐标为(0,3),点B 的坐标为(2,1),点C 的坐标为(2,-3),则经画图操作可知△ABC 的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(-2,-1)
D.(2,0)
4
C
典题精讲
小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A.2 cm B.4 cm
C.6 cm D.8 cm
5
B
易错提醒
若点O 是等腰三角形ABC 的外心,且∠BOC=60°,底边BC=2,则△ABC 的面积为( )
A.2+ B.
C.2+ 或2- D.4+2 或2-
易错点:忽视三角形的外心与三角形的位置关系,出现漏解
C
易错提醒
由题意可得,存在两种情况,当△ABC 为钝角三角形时,如图中的△A1BC,
当△ABC 为锐角三角形时,
如图中的△A2BC.
连接A1A2,交BC 于D.
∵A1B=A1C,A2B=A2C,
∴A1A2垂直平分BC.∴A1A2为⊙O 的直径,BD=CD=1.∵∠BOC=60°,OB=OC,
易错提醒
∴△OBC 为等边三角形.∴OB=OC=BC=2.
∴OD=
∴S△ BC=
S△ BC=
∴△ABC 的面积为2- 或2+
故选C.
学以致用
小试牛刀
如图,△ABC 是⊙O 的内接三角形,∠C=30°,⊙O 的半径为5,若点P 是⊙O 上的一点,在△ABP 中,PB=AB,则PA 的长为( )
A.5
B.
C.5
D.5
1
D
小试牛刀
如图,点A,B,C 均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C 三点外还能
经过的格点数为_______.
2
5
小试牛刀
3 如图,∠BAC 的平分线交△ABC 的外接圆于点D,∠ABC 的平分线交AD 于点E,
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC 的外接圆的半径.
小试牛刀
∵AD 平分∠BAC,BE 平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴BD=CD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,
∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
(1)证明:
小试牛刀
连接CD,如图所示.
∵AD 平分∠BAC,
∴∠BAD=∠CAD,
∴BD=CD.
∴CD=BD=4.
∵∠BAC=90°,
∴BC 是直径,
∴∠BDC=90°,
∴BC=
∴△ABC 的外接圆的半径=
(2)解:
小试牛刀
4 如图,已知等腰直角三角形ABC,点P 是斜边BC 上一点(不与B,C 重合),PE 是△ABP 的外接圆⊙O 的直径.
(1)求证:△APE 是等腰直角三角形;
(2)若⊙O 的直径为2,求PC 2+PB 2的值.
小试牛刀
∵AB=AC,∠BAC =90°,
∴∠C=∠ABC=45°.
∴∠AEP=∠ABP=45°.
∵PE 是⊙O 的直径,∴∠PAE=90°,
∴∠APE=∠AEP=45°.
∴AP=AE.
∴△PAE 是等腰直角三角形.
(1)证明:
小试牛刀
如图,作PM⊥AC 于M,PN⊥AB 于N,
则四边形PMAN 是矩形,∴PM=AN,
易知△PCM,△PNB 都是等腰直角三角形,
∴PC= PM,PB= PN.
∴PC 2+PB 2=2(PM 2+PN 2)
=2(AN 2+PN 2)
=2PA2
=PE 2
=22
=4.
(2)解:
小试牛刀
5 如图,已知△ABC 内接于⊙O,AB 是直径,弦CE⊥AB 于点F,C 是AD 的中点,连接BD 并延长交EC 的延长线于点G,连接AD,分别交CE,BC 于点P,Q,
求证:点P 是△ACQ 的外心.
小试牛刀
∵AB 是直径,
∴∠ACB=90°.
∵AB⊥CE,AB 是直径,∴AC=AE.
又∵AC=CD,
∴CD=AE.
∴∠ACP=∠CAP.
∴AP=PC.又∠QCP+∠ACP=∠CAP+∠CQP=90°,
∴∠PCQ=∠CQP. ∴CP=PQ.
∴CP=AP=PQ,即P 是Rt△ACQ 的外心.
证明:
小试牛刀
6 已知⊙O 是正三角形ABC 的外接圆.
(1)如图①,若PC 为⊙O 的直径,连接AP,BP,
求证:AP+BP=PC.
(2)如图②,若点P 是弧AB 上任意一点,连接AP,BP,CP,那么结论AP+BP=PC 还成立吗?请说明理由.
小试牛刀
∵△ABC 为正三角形,
∴∠ABC=∠BAC=60°.
∴∠APC=∠BPC=60°.
∵PC 为⊙O 的直径,
∴∠PAC=∠PBC=90°.
∴∠ACP=∠BCP=30°.
∴AP=BP= PC.
∴AP+BP=PC.
(1)证明:
小试牛刀
成立.
理由:如图,在PC 上取一点D,使PD=PA,连接AD.
∵∠APD=∠ABC=60°,
∴△APD 为等边三角形.
∴AD=AP,∠PAD=60°.
又∵∠BAC=60°,
∴∠PAB=∠DAC.
又∵AB=AC,
∴△APB ≌ △ADC,
∴PB=DC,
∴AP+BP=PD+DC=PC.
(2)解:
课堂小结
课堂小结
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.
(2)经过一个已知点能作无数个圆.
(3)经过两个已知点A、B 能作无数个圆!这些圆的圆心在线段AB 的垂直平分线上.
(4)不在同一直线上的三个点确定一个圆.
(5)外接圆,外心的概念.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5 确定圆的条件
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、过一点可以作几条直线?
2、过几点可确定一条直线?
过几点可以确定一个圆呢?
新课精讲
探索新知
1
知识点
确定圆的条件
经过一个已知点A 能确定一个圆吗?
A
经过一个已知点能作无数个圆.
你怎样画这个圆?
探索新知
经过两个已知点A、B 能确
定一个圆吗
A
B
它们的圆心都在线段AB 的中垂线上.
经过两个已知点A、B
所作的圆的圆心在怎
样的一条直线上?
经过两个已知点A、B 能作无数个圆
探索新知
A
B
C
过如下三点能不能做圆?为什么?
不在同一直线上的三点确定一个圆
探索新知
如图①是一个残破的圆轮,李师傅想要再浇铸一个
同样大小的圆轮,你能想办法帮助李师傅吗?
例1
导引:
可先在圆弧上任意取三个点,然后作出两条弦,分别作
这两条弦的垂直平分线即可确定圆轮所在圆的圆心.
探索新知
解:
如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC 的垂直平分线
DE,FG,DE,FG 相交于点O;
(3)以O 为圆心,OA 为半径作⊙O,⊙O 就是圆轮所在的圆.
探索新知
总 结
经过不在同一条直线上的三点A,B,C 作圆,圆心O 是线段AB,BC 的垂直平分线的交点,再以OA (或OB,OC )为半径作圆即可,这样的圆只能作一个.
典题精讲
如图,点A,B,C 在同一条直线上,点D 在直线AB 外,过这四点中的任意三个点,能画圆的个数是( )
A.1
B.2
C.3
D.4
1
C
典题精讲
已知AB=4 cm,则过点A,B 且半径为3 cm的圆有( )
A.1个 B.2个
C.3个 D.4个
2
B
下列说法中正确的是( )
A.两个点确定一个圆
B.三个点确定一个圆
C.四个点确定一个圆
D.不共线的三个点确定一个圆
3
C
典题精讲
如图,在5×5的正方形网格中,一条圆弧经过A,B,C 三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
4
B
探索新知
2
知识点
三角形的外接圆、外心
已知△ABC,用直尺和圆规作出过点A、B、C 的圆.
A
B
C
O
探索新知
定 义
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
探索新知
如图:⊙O 是△ABC 的外接圆, △ABC 是⊙O 的内接三角形,点O 是△ABC 的外心.
外心是△ABC 三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
探索新知
三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一点的距离为半径作圆即可.
探索新知
如图,在平面直角坐标系中,点A,B,C 的坐标分别为(1,4),(5,4),(1,-2),则△ABC 外接圆的圆心坐标是( )
A.(2,3)
B.(3,2)
C.(1,3)
D.(3,1)
例2
D
探索新知
导引:
由A (1,4),B (5,4)可知AB∥x 轴,△ABC 的外接圆
圆心在线段AB 的垂直平分线上,所以圆心的横坐标
应为 =3;同理,圆心还应在线段AC 的垂直平
分线上,其纵坐标应为 =1.
探索新知
总 结
根据垂径定理的推论“弦的垂直平分线必过圆心”,作两条弦的垂直平分线,交点即为圆心.
探索新知
如图1,△ABC 内接于⊙O,∠C=45°,AB=4,求⊙O 的半径.
例3
图1
探索新知
导引:
要求⊙O 的半径,已知弦AB 的长,需以AB 为边与
⊙O 的半径(或直径)构成等腰直角三角形,因此有
两个切入点.方法一:如图2,连接OA,OB,利
用圆周角定理可得∠AOB=2∠C=90°,再利用
勾股定理求出半径;方法二:
如图2,作直径AD,连接BD,
利用同弧所对的圆周角相等,得
∠D=∠C=45°,再利用勾股
定理可求出半径.
图2
探索新知
解:
方法一:如图1,连接OA,OB,设⊙O 的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB 2=AB 2,即r 2+r 2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O 的半径为2 .
图1
探索新知
方法二:如图2,作直径AD,连接BD,设⊙O 的半径为r.
∵AD 为⊙O 的直径,
∴∠ABD=90°.
又∵∠D=∠C=45°,∴∠DAB=45°.
∴BD=AB=4.
在Rt△ABD 中,AB 2+BD 2=AD 2,即42+42=(2r )2
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O 的半径为2 .
图2
探索新知
总 结
求三角形的外接圆半径时,最常用的办法是作出圆心与三角形顶点的连线(即半径),延长使这条半径变为直径,将求半径转化为直角三角形中求边的长.
典题精讲
已知下面的三个三角形,分别作出它们的外接圆. 它们外心的位置有怎样的特点?
1
解:作图略.经观察发现:锐角三角形的外心在三角形的内部;
直角三角形的外心在斜边的中点处;钝角三角形的外心在三
角形的外部.
典题精讲
下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;
② 任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内;
④三角形的外心到三角形三边的距离相等;
⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4
2
B
典题精讲
如图,AC,BE 是⊙O 的直径,弦AD 与BE 交于点F,下列三角形中,外心不是点O 的是( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE
3
B
典题精讲
如图,在平面直角坐标系xOy 中,点A 的坐标为(0,3),点B 的坐标为(2,1),点C 的坐标为(2,-3),则经画图操作可知△ABC 的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(-2,-1)
D.(2,0)
4
C
典题精讲
小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A.2 cm B.4 cm
C.6 cm D.8 cm
5
B
易错提醒
若点O 是等腰三角形ABC 的外心,且∠BOC=60°,底边BC=2,则△ABC 的面积为( )
A.2+ B.
C.2+ 或2- D.4+2 或2-
易错点:忽视三角形的外心与三角形的位置关系,出现漏解
C
易错提醒
由题意可得,存在两种情况,当△ABC 为钝角三角形时,如图中的△A1BC,
当△ABC 为锐角三角形时,
如图中的△A2BC.
连接A1A2,交BC 于D.
∵A1B=A1C,A2B=A2C,
∴A1A2垂直平分BC.∴A1A2为⊙O 的直径,BD=CD=1.∵∠BOC=60°,OB=OC,
易错提醒
∴△OBC 为等边三角形.∴OB=OC=BC=2.
∴OD=
∴S△ BC=
S△ BC=
∴△ABC 的面积为2- 或2+
故选C.
学以致用
小试牛刀
如图,△ABC 是⊙O 的内接三角形,∠C=30°,⊙O 的半径为5,若点P 是⊙O 上的一点,在△ABP 中,PB=AB,则PA 的长为( )
A.5
B.
C.5
D.5
1
D
小试牛刀
如图,点A,B,C 均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C 三点外还能
经过的格点数为_______.
2
5
小试牛刀
3 如图,∠BAC 的平分线交△ABC 的外接圆于点D,∠ABC 的平分线交AD 于点E,
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC 的外接圆的半径.
小试牛刀
∵AD 平分∠BAC,BE 平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴BD=CD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,
∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
(1)证明:
小试牛刀
连接CD,如图所示.
∵AD 平分∠BAC,
∴∠BAD=∠CAD,
∴BD=CD.
∴CD=BD=4.
∵∠BAC=90°,
∴BC 是直径,
∴∠BDC=90°,
∴BC=
∴△ABC 的外接圆的半径=
(2)解:
小试牛刀
4 如图,已知等腰直角三角形ABC,点P 是斜边BC 上一点(不与B,C 重合),PE 是△ABP 的外接圆⊙O 的直径.
(1)求证:△APE 是等腰直角三角形;
(2)若⊙O 的直径为2,求PC 2+PB 2的值.
小试牛刀
∵AB=AC,∠BAC =90°,
∴∠C=∠ABC=45°.
∴∠AEP=∠ABP=45°.
∵PE 是⊙O 的直径,∴∠PAE=90°,
∴∠APE=∠AEP=45°.
∴AP=AE.
∴△PAE 是等腰直角三角形.
(1)证明:
小试牛刀
如图,作PM⊥AC 于M,PN⊥AB 于N,
则四边形PMAN 是矩形,∴PM=AN,
易知△PCM,△PNB 都是等腰直角三角形,
∴PC= PM,PB= PN.
∴PC 2+PB 2=2(PM 2+PN 2)
=2(AN 2+PN 2)
=2PA2
=PE 2
=22
=4.
(2)解:
小试牛刀
5 如图,已知△ABC 内接于⊙O,AB 是直径,弦CE⊥AB 于点F,C 是AD 的中点,连接BD 并延长交EC 的延长线于点G,连接AD,分别交CE,BC 于点P,Q,
求证:点P 是△ACQ 的外心.
小试牛刀
∵AB 是直径,
∴∠ACB=90°.
∵AB⊥CE,AB 是直径,∴AC=AE.
又∵AC=CD,
∴CD=AE.
∴∠ACP=∠CAP.
∴AP=PC.又∠QCP+∠ACP=∠CAP+∠CQP=90°,
∴∠PCQ=∠CQP. ∴CP=PQ.
∴CP=AP=PQ,即P 是Rt△ACQ 的外心.
证明:
小试牛刀
6 已知⊙O 是正三角形ABC 的外接圆.
(1)如图①,若PC 为⊙O 的直径,连接AP,BP,
求证:AP+BP=PC.
(2)如图②,若点P 是弧AB 上任意一点,连接AP,BP,CP,那么结论AP+BP=PC 还成立吗?请说明理由.
小试牛刀
∵△ABC 为正三角形,
∴∠ABC=∠BAC=60°.
∴∠APC=∠BPC=60°.
∵PC 为⊙O 的直径,
∴∠PAC=∠PBC=90°.
∴∠ACP=∠BCP=30°.
∴AP=BP= PC.
∴AP+BP=PC.
(1)证明:
小试牛刀
成立.
理由:如图,在PC 上取一点D,使PD=PA,连接AD.
∵∠APD=∠ABC=60°,
∴△APD 为等边三角形.
∴AD=AP,∠PAD=60°.
又∵∠BAC=60°,
∴∠PAB=∠DAC.
又∵AB=AC,
∴△APB ≌ △ADC,
∴PB=DC,
∴AP+BP=PD+DC=PC.
(2)解:
课堂小结
课堂小结
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.
(2)经过一个已知点能作无数个圆.
(3)经过两个已知点A、B 能作无数个圆!这些圆的圆心在线段AB 的垂直平分线上.
(4)不在同一直线上的三个点确定一个圆.
(5)外接圆,外心的概念.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
