【班海精品】北师大版(新)九年级下-3.4圆周角和圆心角的关系 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-3.4圆周角和圆心角的关系 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览








文档简介
(共52张PPT)
4 圆周角和圆心角的关系
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
什么是圆心角?它具有哪些性质?
新课精讲
探索新知
1
知识点
圆周角的定义
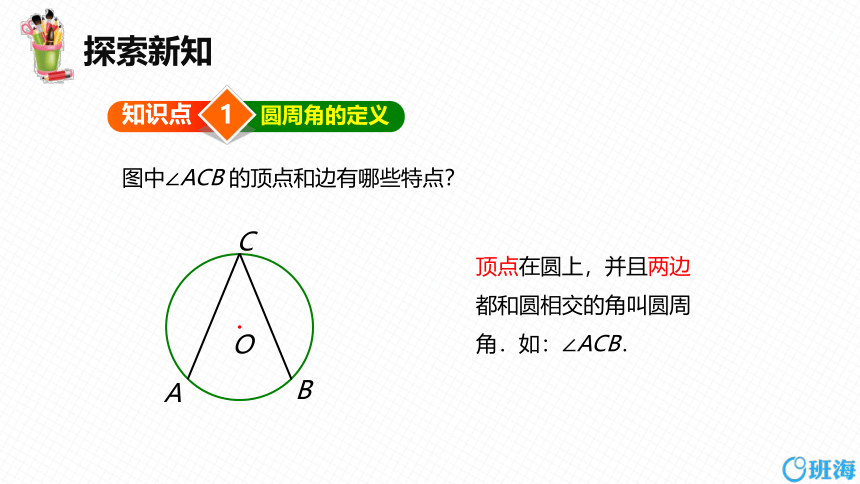
图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
顶点在圆上,并且两边都和圆相交的角叫圆周角.如:∠ACB.
探索新知
圆周角的特征:
①角的顶点在圆上;
②角的两边都与圆相交,这两个特征是判定圆周角不可缺少的条件.
探索新知
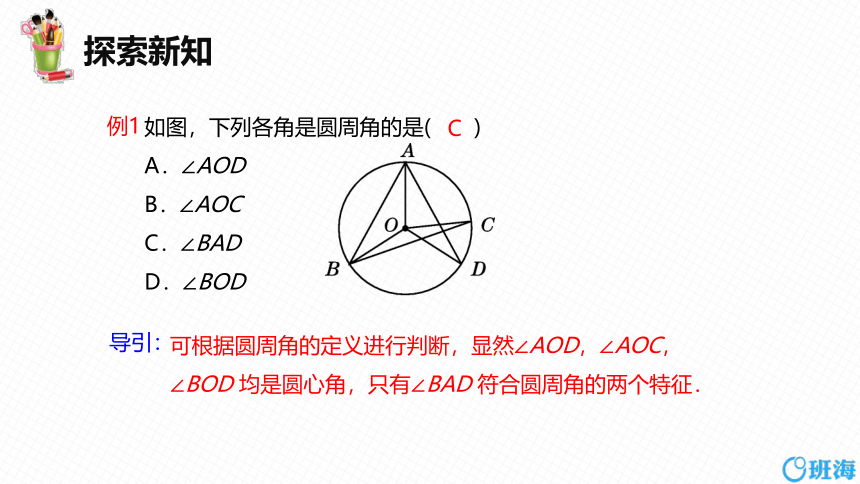
如图,下列各角是圆周角的是( )
A.∠AOD
B.∠AOC
C.∠BAD
D.∠BOD
可根据圆周角的定义进行判断,显然∠AOD,∠AOC,∠BOD 均是圆心角,只有∠BAD 符合圆周角的两个特征.
导引:
例1
C
探索新知
总 结
判断一个角是否为圆周角,关键是看这个角是否具备圆周角的两个特征:
(1)角的顶点在圆上;
(2)角的两边都与圆相交,二者缺一不可.
典题精讲
下列四个图中,∠x 为圆周角的是( )
1
C
典题精讲
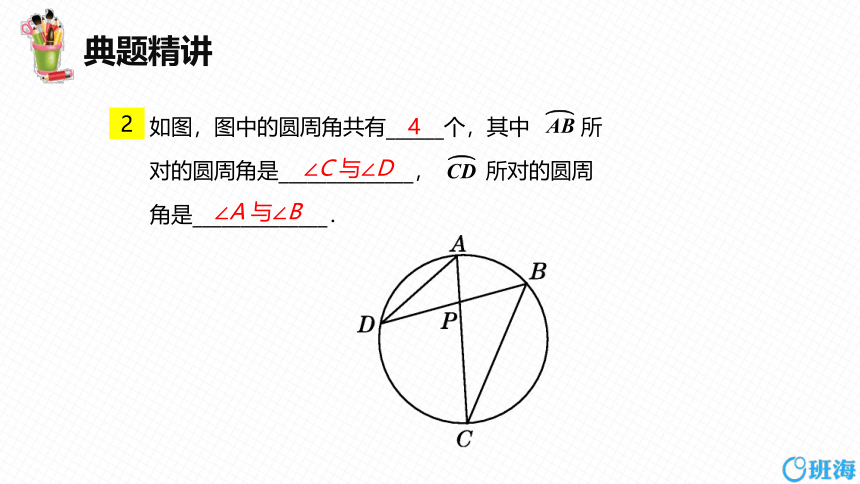
如图,图中的圆周角共有______个,其中 所
对的圆周角是______________, 所对的圆周
角是______________.
2
4
∠C 与∠D
∠A 与∠B
探索新知
2
知识点
圆周角和圆心角的关系
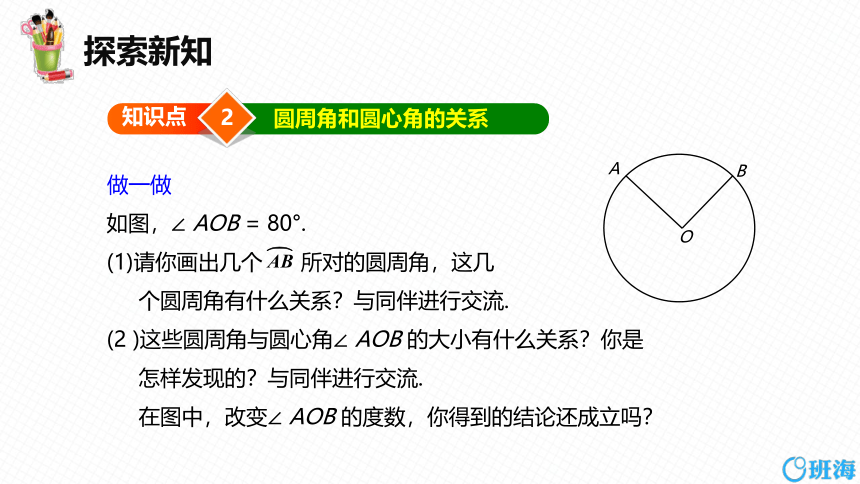
如图,∠ AOB = 80°.
(1)请你画出几个 所对的圆周角,这几
个圆周角有什么关系?与同伴进行交流.
(2 )这些圆周角与圆心角∠ AOB 的大小有什么关系?你是
怎样发现的?与同伴进行交流.
在图中,改变∠ AOB 的度数,你得到的结论还成立吗?
做一做
O
A
B
探索新知
归 纳
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
探索新知
1. 圆周角定理的证明:
已知:如图,∠ C 是 所对的圆周角, ∠ AOB 是
所对的圆心角.
求证: ∠ C= ∠ AOB
分析:根据圆周角和圆心的位置关系,分三种情况讨论:
探索新知
(1)圆心O 在∠ C 的一条边上,如图 (1).
∵ ∠ AOB 是△AOC 的外角,∴ ∠ AOB = ∠ A + ∠ C.
∵ OA = OC,∴ ∠ A = ∠ C.
∴ ∠ AOB = 2 ∠ C,
即 ∠ C = ∠ AOB.
请你完成图 (2)和图 (3)两种情况的证明.
证明:
(1)圆心O 在∠ C 的一条边上,如图 (1);
(2)圆心O 在∠ C 的内部,如图 (2);
(3)圆心O 在∠ C 的外部,如图 (3).
在三种位置关系中,我们选择(1)给出证明,其他情况可以
转化为(1)的情况进行证明.
探索新知
如图,A,B,C,D 是同一圆上的点,∠1=68°,∠A=40°,则∠D=________.
例2
由圆周角定理的推论1可知
∠C=∠A=40°,由三角
形的外角性质得
∠D=∠1-∠C=68°-40°
=28°.
导引:
28°
探索新知
总 结
本题应用转化思想,利用“同弧所对的圆周角相等”将已知角转化为与要求的角在同一个三角形中的角,然后利用三角形的外角性质求解.
探索新知
如图,在⊙O 中,∠AOC=150°,求∠ABC,∠ADC 的度数,并判断∠ABC 和∠ADC,∠EBC 和∠ADC 之间的度数关系.
例3
解题的关键是分清同弧所对的圆
心角和圆周角,如 所对的圆
心角是∠AOC,所对的圆周角是∠ABC,
所对的圆心角是大于平角的∠α,所对的圆周
角是∠ADC.
导引:
探索新知
∵∠AOC=150°,∴∠ABC= ∠AOC=75°.
∵∠α=360°-∠AOC=360°-150°=210°,
∴∠ADC= ∠α=105°.
∵∠EBC=180°-∠ABC=180°-75°=105°,
∴∠EBC=∠ADC,即∠EBC 与∠ADC 相等.
又∵∠ABC+∠ADC=75°+105°=180°,
∴∠ABC 和∠ADC 互补.
解:
典题精讲
如图,在⊙O 中,∠O = 50°,求∠A 的度数.
1
解:∵∠BAC 与∠BOC
所对的弧都是 ,
∴∠BAC= ∠BOC= ×50°
=25°.
O
A
B
C
典题精讲
将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B 的读数分别为100°,150°,则∠ACB=________.
2
25°
典题精讲
如图,点A,B,C 都在⊙O上,且点C 在弦AB 所对的优弧上,如果∠AOB=64°,那么∠ACB 的度数是( )
A.26°
B.30°
C.32°
D.64°
3
C
典题精讲
如图,在⊙O 中,AB 是直径,CD 是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
4
D
典题精讲
如图,AB 是⊙O 的直径,弦CD⊥AB 于点E,∠CDB=30°,⊙O 的半径为5 cm,则圆心O 到弦CD 的距离为( )
A. cm
B.3 cm
C.3 cm
D.6 cm
5
A
探索新知
3
知识点
同弧或等弧所对的圆周角
想一想
在如图的射门游戏中,当球员在B ,D,E 处射门时,所形成的三个张角∠ ABC, ∠ ADC, ∠ AEC 的大小有什么关系?你能用圆周角定理证明你的结论吗?
探索新知
归 纳
推论 同弧或等弧所对的圆周角相等.
探索新知
如图,在⊙O 中,∠ACB=∠BDC=60°,AC=2 cm.
(1)求∠BAC 的度数;
(2)求⊙O 的周长.
例4
(1)观察图形发现∠BAC 与∠BDC 为同弧所对的圆周角,
故∠BAC=∠BDC=60°;(2)要求圆的周长,需先求出
半径,可利用垂径定理,即连接OA,作OE ⊥AC 于点E,
构造直角三角形求出半径.
导引:
探索新知
解:
(1)在⊙O 中,∠BDC 与∠BAC 均为 所对的圆周角,
∴∠BAC=∠BDC=60°.
(2)∵∠ACB=60°,又由(1)知∠BAC=60°,
∴△ABC 为等边三角形.连接OA,作OE ⊥AC 于点E,
如图所示.
∵OE⊥AC,AC=2 cm,∴AE= cm.
在Rt△AOE 中,∠AOE=∠ABC=60°,
∴∠OAE=30°. ∴OE= OA.
又∵OE 2+AE 2=OA 2,∴OA=2 cm.
∴⊙O 的周长为2π×2=4π(cm).
探索新知
总 结
同一条弧所对的圆周角有无数个,它们都相等,这里特别要注意不要误认为 “同弦所对的圆周角”相等 , 因为一条弦(非直径)所对的圆周角的大小有两种.
典题精讲
如图,哪个角与∠BAC 相等?你还能找到哪些相等的角?
1
解:∠BDC=∠BAC,如图,
相等的角还有∠ADB=∠ACB,
∠ACD=∠ABD,
∠CAD=∠CBD,
∠1=∠2,∠3=∠4.
A
B
C
D
典题精讲
如图,⊙O 的直径AB 垂直于弦CD,∠CAB=36°,则∠BCD 的大小是( )
A.18°
B.36°
C.54°
D.72°
2
B
典题精讲
如图,在⊙O 中,AB=BC,点D 在⊙O上,∠CDB=25°,则∠AOB=( )
A.45°
B.50°
C.55°
D.60°
3
︵
︵
B
典题精讲
如图,在⊙O 中,OA⊥BC,∠AOB=70°,则∠ADC 的度数为( )
A.30°
B.35°
C.45°
D.70°
4
B
易错提醒
如图,⊙O 的直径AB 垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD 的长为( )
A.2 B.4 C.4 D.8
易错点:忽视勾股定理的应用而致错
C
学以致用
小试牛刀
如图,B,C 是⊙A上的两点,AB 的垂直平分线与⊙A 交于E,F 两点,与线段AC 交于点D. 若∠BFC=20°,则∠DBC=( )
A.30°
B.29°
C.28°
D.20°
1
A
小试牛刀
如图,A,B,C 是⊙O上的三点,且四边形ABCO 是平行四边形,OF⊥OC 交⊙O 于点F,则∠BAF 等于( )
A.12.5°
B.15°
C.20°
D.22.5°
2
B
小试牛刀
3 如图,在⊙O 中,弦AB,CD 垂直相交于点E.
求证:∠BOC+∠AOD=180°.
小试牛刀
连接AC,因为圆周角∠BAC 与圆心角∠BOC 同是BC 所对的角,所以∠BOC=2∠BAC.
因为圆周角∠ACD 与圆心角∠AOD 同是AD 所对的角,所以∠AOD=2∠ACD.
在Rt△ACE 中,∠BAC+∠ACD=90°,
所以∠BOC+∠AOD=2∠BAC+2∠ACD=2(∠BAC+∠ACD )=2×90°=180°.
证明:
小试牛刀
4 如图,AB 是⊙O 的直径,点C 是AE 的中点,CD⊥AB 于点D,交AE 于点F,连接AC,求证:AF=CF.
小试牛刀
方法一:连接BC,如图①.
∵AB 是⊙O 的直径,∴∠ACB=90°,
即∠ACF+∠BCD=90°.
∵CD⊥AB,∴∠B+∠BCD=90°.
∴∠B=∠ACF.又∵点C 是AE 的中点,
∴AC=CE.∴∠B=∠CAE.∴∠ACF=∠CAE.∴AF=CF.
方法二:如图②,延长CD 交⊙O 于点H.
∵AB 是⊙O 的直径,CD⊥AB,∴AC=AH.
又∵点C 是AE 的中点,∴AC=CE.
∴AH=CE.∴∠ACF=∠CAF. ∴AF=CF.
证明:
小试牛刀
方法三:连接OC,如图③.
∵AC=CE,OC 过圆心,∴CO⊥AE.
∴∠COD+∠OAE=90°.
∵CD⊥OA,∴∠DOC+∠DCO=90°.
∴∠DCO=∠DAE.
∵OC=OA,∴∠OCA=∠OAC.
∴∠FCA=∠CAF. ∴AF=CF.
小试牛刀
5 如图,AB 为⊙O 的一条弦,点C 是劣弧AB 的中点,E 是优弧AB 上一点,点F 在AE 的延长线上,且BE=EF,线段CE交弦AB 于点D.
(1)求证:CE∥BF;
(2)若线段BD 的长为2,且EA∶EB∶EC=3∶1∶ ,求△BCD 的面积(注:根据圆的对称性可知OC⊥AB ).
小试牛刀
∵AC=CB,∴∠AEC=∠CEB.
∵BE=EF,∴∠EBF=∠EFB.
∵∠AEB 为△BEF 的外角,
∴∠AEB=∠EBF+∠EFB,
即2∠CEB=2∠EBF.
∴∠CEB=∠EBF,∴CE∥BF.
(1)证明:
小试牛刀
如图,设AB 交OC 于点G.
∵CE∥BF,∴
∵EA∶EB=3∶1,
BE=EF,∴
∵DB=2,∴AD=6.
∵∠AEC=∠CEB,∠A=∠BCE,
∴△ADE∽△CBE,
∴
∴CB=2
(2)解:
小试牛刀
∵CO⊥AB,∴BG=(6+2)÷2=4.
∴CG=
∴S△BCD= BD CG= ×2×2=2.
小试牛刀
6 如图,⊙O 的半径为1,A,P,B,C 是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC 的形状:______________.
(2)试探究线段PA,PB,PC 之间的数量关系,并说明理由.
(3)当点P 位于AB 的什么位置时,四边形APBC 的面积最大?求出最大面积.
等边三角形
小试牛刀
(2)PA+PB=PC.
理由:如图①,在PC 上截取PD=PA,连接AD.
∵∠APC=60°,
∴△PAD 是等边三角形.
∴PA=AD,∠PAD=60°.
∵∠BAC=60°,∴∠PAD=∠BAC. ∴∠PAB=∠DAC.
又∵AB=AC,∠ABP=∠ACD,∴△PAB ≌ △DAC.
∴PB=DC.∵PD+DC=PC,∴PA+PB=PC.
解:
小试牛刀
(3)当点P 为AB 的中点时,四边形APBC 的面积最大.
如图②,过点P 作PE⊥AB,垂足为E,过点C 作CF⊥AB,垂足为F.
∵△ABC 是等边三角形,
∴点F 为AB 的中点,且CF 过圆心O.
∵S△PAB= AB PE,S△ABC= AB CF,
∴S四边形APBC= AB (PE+CF).
当点P 为AB 的中点时,点E 与点F 重合,PE+CF=PC,PC 为⊙O 的直径.∴此时四边形APBC 的面积最大.
易求得AB= ,∴S四边形APBC= ×2× =
课堂小结
课堂小结
(1)一个概念(圆周角);
(2)一个定理:一条弧所对的圆周角等于该弧所对的
圆心角的一半;
(3)一个推论:同圆内,同弧或等弧所对的圆周角相
等. 相等的圆周角所对的弧相等;
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4 圆周角和圆心角的关系
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
什么是圆心角?它具有哪些性质?
新课精讲
探索新知
1
知识点
圆周角的定义
图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
顶点在圆上,并且两边都和圆相交的角叫圆周角.如:∠ACB.
探索新知
圆周角的特征:
①角的顶点在圆上;
②角的两边都与圆相交,这两个特征是判定圆周角不可缺少的条件.
探索新知
如图,下列各角是圆周角的是( )
A.∠AOD
B.∠AOC
C.∠BAD
D.∠BOD
可根据圆周角的定义进行判断,显然∠AOD,∠AOC,∠BOD 均是圆心角,只有∠BAD 符合圆周角的两个特征.
导引:
例1
C
探索新知
总 结
判断一个角是否为圆周角,关键是看这个角是否具备圆周角的两个特征:
(1)角的顶点在圆上;
(2)角的两边都与圆相交,二者缺一不可.
典题精讲
下列四个图中,∠x 为圆周角的是( )
1
C
典题精讲
如图,图中的圆周角共有______个,其中 所
对的圆周角是______________, 所对的圆周
角是______________.
2
4
∠C 与∠D
∠A 与∠B
探索新知
2
知识点
圆周角和圆心角的关系
如图,∠ AOB = 80°.
(1)请你画出几个 所对的圆周角,这几
个圆周角有什么关系?与同伴进行交流.
(2 )这些圆周角与圆心角∠ AOB 的大小有什么关系?你是
怎样发现的?与同伴进行交流.
在图中,改变∠ AOB 的度数,你得到的结论还成立吗?
做一做
O
A
B
探索新知
归 纳
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
探索新知
1. 圆周角定理的证明:
已知:如图,∠ C 是 所对的圆周角, ∠ AOB 是
所对的圆心角.
求证: ∠ C= ∠ AOB
分析:根据圆周角和圆心的位置关系,分三种情况讨论:
探索新知
(1)圆心O 在∠ C 的一条边上,如图 (1).
∵ ∠ AOB 是△AOC 的外角,∴ ∠ AOB = ∠ A + ∠ C.
∵ OA = OC,∴ ∠ A = ∠ C.
∴ ∠ AOB = 2 ∠ C,
即 ∠ C = ∠ AOB.
请你完成图 (2)和图 (3)两种情况的证明.
证明:
(1)圆心O 在∠ C 的一条边上,如图 (1);
(2)圆心O 在∠ C 的内部,如图 (2);
(3)圆心O 在∠ C 的外部,如图 (3).
在三种位置关系中,我们选择(1)给出证明,其他情况可以
转化为(1)的情况进行证明.
探索新知
如图,A,B,C,D 是同一圆上的点,∠1=68°,∠A=40°,则∠D=________.
例2
由圆周角定理的推论1可知
∠C=∠A=40°,由三角
形的外角性质得
∠D=∠1-∠C=68°-40°
=28°.
导引:
28°
探索新知
总 结
本题应用转化思想,利用“同弧所对的圆周角相等”将已知角转化为与要求的角在同一个三角形中的角,然后利用三角形的外角性质求解.
探索新知
如图,在⊙O 中,∠AOC=150°,求∠ABC,∠ADC 的度数,并判断∠ABC 和∠ADC,∠EBC 和∠ADC 之间的度数关系.
例3
解题的关键是分清同弧所对的圆
心角和圆周角,如 所对的圆
心角是∠AOC,所对的圆周角是∠ABC,
所对的圆心角是大于平角的∠α,所对的圆周
角是∠ADC.
导引:
探索新知
∵∠AOC=150°,∴∠ABC= ∠AOC=75°.
∵∠α=360°-∠AOC=360°-150°=210°,
∴∠ADC= ∠α=105°.
∵∠EBC=180°-∠ABC=180°-75°=105°,
∴∠EBC=∠ADC,即∠EBC 与∠ADC 相等.
又∵∠ABC+∠ADC=75°+105°=180°,
∴∠ABC 和∠ADC 互补.
解:
典题精讲
如图,在⊙O 中,∠O = 50°,求∠A 的度数.
1
解:∵∠BAC 与∠BOC
所对的弧都是 ,
∴∠BAC= ∠BOC= ×50°
=25°.
O
A
B
C
典题精讲
将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B 的读数分别为100°,150°,则∠ACB=________.
2
25°
典题精讲
如图,点A,B,C 都在⊙O上,且点C 在弦AB 所对的优弧上,如果∠AOB=64°,那么∠ACB 的度数是( )
A.26°
B.30°
C.32°
D.64°
3
C
典题精讲
如图,在⊙O 中,AB 是直径,CD 是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
4
D
典题精讲
如图,AB 是⊙O 的直径,弦CD⊥AB 于点E,∠CDB=30°,⊙O 的半径为5 cm,则圆心O 到弦CD 的距离为( )
A. cm
B.3 cm
C.3 cm
D.6 cm
5
A
探索新知
3
知识点
同弧或等弧所对的圆周角
想一想
在如图的射门游戏中,当球员在B ,D,E 处射门时,所形成的三个张角∠ ABC, ∠ ADC, ∠ AEC 的大小有什么关系?你能用圆周角定理证明你的结论吗?
探索新知
归 纳
推论 同弧或等弧所对的圆周角相等.
探索新知
如图,在⊙O 中,∠ACB=∠BDC=60°,AC=2 cm.
(1)求∠BAC 的度数;
(2)求⊙O 的周长.
例4
(1)观察图形发现∠BAC 与∠BDC 为同弧所对的圆周角,
故∠BAC=∠BDC=60°;(2)要求圆的周长,需先求出
半径,可利用垂径定理,即连接OA,作OE ⊥AC 于点E,
构造直角三角形求出半径.
导引:
探索新知
解:
(1)在⊙O 中,∠BDC 与∠BAC 均为 所对的圆周角,
∴∠BAC=∠BDC=60°.
(2)∵∠ACB=60°,又由(1)知∠BAC=60°,
∴△ABC 为等边三角形.连接OA,作OE ⊥AC 于点E,
如图所示.
∵OE⊥AC,AC=2 cm,∴AE= cm.
在Rt△AOE 中,∠AOE=∠ABC=60°,
∴∠OAE=30°. ∴OE= OA.
又∵OE 2+AE 2=OA 2,∴OA=2 cm.
∴⊙O 的周长为2π×2=4π(cm).
探索新知
总 结
同一条弧所对的圆周角有无数个,它们都相等,这里特别要注意不要误认为 “同弦所对的圆周角”相等 , 因为一条弦(非直径)所对的圆周角的大小有两种.
典题精讲
如图,哪个角与∠BAC 相等?你还能找到哪些相等的角?
1
解:∠BDC=∠BAC,如图,
相等的角还有∠ADB=∠ACB,
∠ACD=∠ABD,
∠CAD=∠CBD,
∠1=∠2,∠3=∠4.
A
B
C
D
典题精讲
如图,⊙O 的直径AB 垂直于弦CD,∠CAB=36°,则∠BCD 的大小是( )
A.18°
B.36°
C.54°
D.72°
2
B
典题精讲
如图,在⊙O 中,AB=BC,点D 在⊙O上,∠CDB=25°,则∠AOB=( )
A.45°
B.50°
C.55°
D.60°
3
︵
︵
B
典题精讲
如图,在⊙O 中,OA⊥BC,∠AOB=70°,则∠ADC 的度数为( )
A.30°
B.35°
C.45°
D.70°
4
B
易错提醒
如图,⊙O 的直径AB 垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD 的长为( )
A.2 B.4 C.4 D.8
易错点:忽视勾股定理的应用而致错
C
学以致用
小试牛刀
如图,B,C 是⊙A上的两点,AB 的垂直平分线与⊙A 交于E,F 两点,与线段AC 交于点D. 若∠BFC=20°,则∠DBC=( )
A.30°
B.29°
C.28°
D.20°
1
A
小试牛刀
如图,A,B,C 是⊙O上的三点,且四边形ABCO 是平行四边形,OF⊥OC 交⊙O 于点F,则∠BAF 等于( )
A.12.5°
B.15°
C.20°
D.22.5°
2
B
小试牛刀
3 如图,在⊙O 中,弦AB,CD 垂直相交于点E.
求证:∠BOC+∠AOD=180°.
小试牛刀
连接AC,因为圆周角∠BAC 与圆心角∠BOC 同是BC 所对的角,所以∠BOC=2∠BAC.
因为圆周角∠ACD 与圆心角∠AOD 同是AD 所对的角,所以∠AOD=2∠ACD.
在Rt△ACE 中,∠BAC+∠ACD=90°,
所以∠BOC+∠AOD=2∠BAC+2∠ACD=2(∠BAC+∠ACD )=2×90°=180°.
证明:
小试牛刀
4 如图,AB 是⊙O 的直径,点C 是AE 的中点,CD⊥AB 于点D,交AE 于点F,连接AC,求证:AF=CF.
小试牛刀
方法一:连接BC,如图①.
∵AB 是⊙O 的直径,∴∠ACB=90°,
即∠ACF+∠BCD=90°.
∵CD⊥AB,∴∠B+∠BCD=90°.
∴∠B=∠ACF.又∵点C 是AE 的中点,
∴AC=CE.∴∠B=∠CAE.∴∠ACF=∠CAE.∴AF=CF.
方法二:如图②,延长CD 交⊙O 于点H.
∵AB 是⊙O 的直径,CD⊥AB,∴AC=AH.
又∵点C 是AE 的中点,∴AC=CE.
∴AH=CE.∴∠ACF=∠CAF. ∴AF=CF.
证明:
小试牛刀
方法三:连接OC,如图③.
∵AC=CE,OC 过圆心,∴CO⊥AE.
∴∠COD+∠OAE=90°.
∵CD⊥OA,∴∠DOC+∠DCO=90°.
∴∠DCO=∠DAE.
∵OC=OA,∴∠OCA=∠OAC.
∴∠FCA=∠CAF. ∴AF=CF.
小试牛刀
5 如图,AB 为⊙O 的一条弦,点C 是劣弧AB 的中点,E 是优弧AB 上一点,点F 在AE 的延长线上,且BE=EF,线段CE交弦AB 于点D.
(1)求证:CE∥BF;
(2)若线段BD 的长为2,且EA∶EB∶EC=3∶1∶ ,求△BCD 的面积(注:根据圆的对称性可知OC⊥AB ).
小试牛刀
∵AC=CB,∴∠AEC=∠CEB.
∵BE=EF,∴∠EBF=∠EFB.
∵∠AEB 为△BEF 的外角,
∴∠AEB=∠EBF+∠EFB,
即2∠CEB=2∠EBF.
∴∠CEB=∠EBF,∴CE∥BF.
(1)证明:
小试牛刀
如图,设AB 交OC 于点G.
∵CE∥BF,∴
∵EA∶EB=3∶1,
BE=EF,∴
∵DB=2,∴AD=6.
∵∠AEC=∠CEB,∠A=∠BCE,
∴△ADE∽△CBE,
∴
∴CB=2
(2)解:
小试牛刀
∵CO⊥AB,∴BG=(6+2)÷2=4.
∴CG=
∴S△BCD= BD CG= ×2×2=2.
小试牛刀
6 如图,⊙O 的半径为1,A,P,B,C 是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC 的形状:______________.
(2)试探究线段PA,PB,PC 之间的数量关系,并说明理由.
(3)当点P 位于AB 的什么位置时,四边形APBC 的面积最大?求出最大面积.
等边三角形
小试牛刀
(2)PA+PB=PC.
理由:如图①,在PC 上截取PD=PA,连接AD.
∵∠APC=60°,
∴△PAD 是等边三角形.
∴PA=AD,∠PAD=60°.
∵∠BAC=60°,∴∠PAD=∠BAC. ∴∠PAB=∠DAC.
又∵AB=AC,∠ABP=∠ACD,∴△PAB ≌ △DAC.
∴PB=DC.∵PD+DC=PC,∴PA+PB=PC.
解:
小试牛刀
(3)当点P 为AB 的中点时,四边形APBC 的面积最大.
如图②,过点P 作PE⊥AB,垂足为E,过点C 作CF⊥AB,垂足为F.
∵△ABC 是等边三角形,
∴点F 为AB 的中点,且CF 过圆心O.
∵S△PAB= AB PE,S△ABC= AB CF,
∴S四边形APBC= AB (PE+CF).
当点P 为AB 的中点时,点E 与点F 重合,PE+CF=PC,PC 为⊙O 的直径.∴此时四边形APBC 的面积最大.
易求得AB= ,∴S四边形APBC= ×2× =
课堂小结
课堂小结
(1)一个概念(圆周角);
(2)一个定理:一条弧所对的圆周角等于该弧所对的
圆心角的一半;
(3)一个推论:同圆内,同弧或等弧所对的圆周角相
等. 相等的圆周角所对的弧相等;
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
