【班海精品】北师大版(新)九年级下-3.6直线和圆的位置关系 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-3.6直线和圆的位置关系 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览








文档简介
(共44张PPT)
6 直线和圆的位置关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
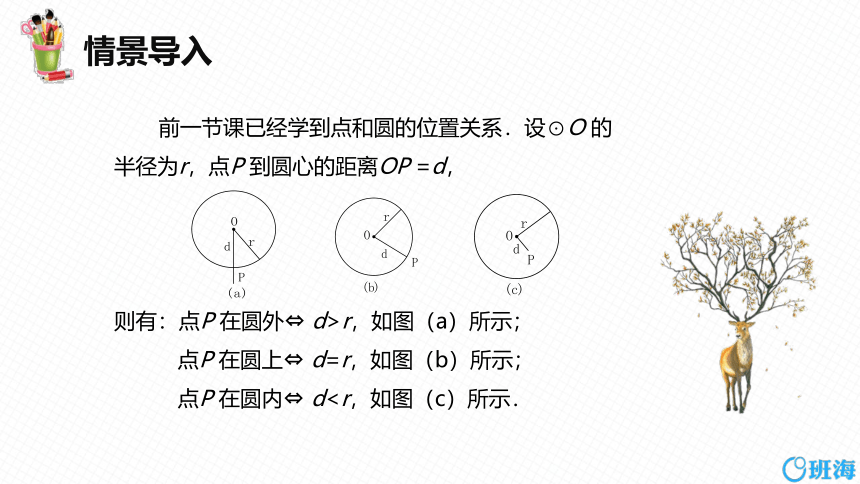
前一节课已经学到点和圆的位置关系.设⊙O 的
半径为r,点P 到圆心的距离OP =d,
则有:点P 在圆外 d>r,如图(a)所示;
点P 在圆上 d=r,如图(b)所示;
点P 在圆内 d新课精讲
探索新知
1
知识点
切线的性质定理
前面我们已学过的切线的性质有哪些?
答:①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
切线还有什么性质?
切线的性质定理:圆的切线垂直于过切点的半径.
探索新知
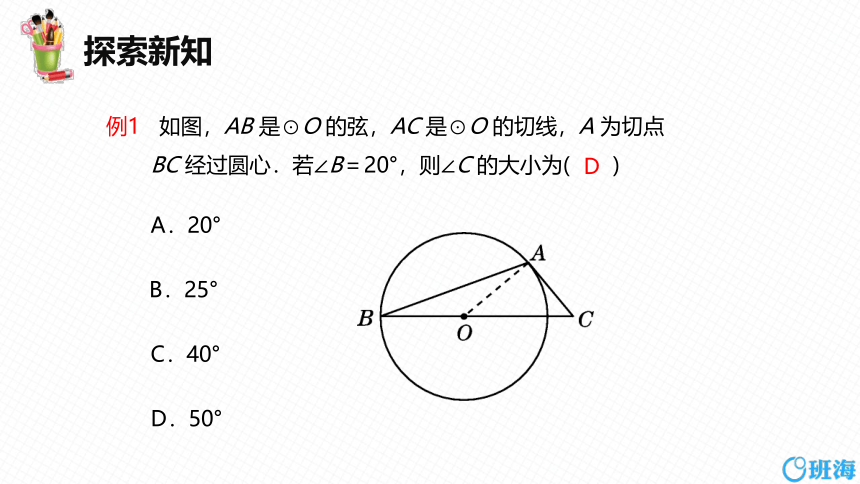
例1 如图,AB 是⊙O 的弦,AC 是⊙O 的切线,A 为切点
BC 经过圆心.若∠B=20°,则∠C 的大小为( )
A.20°
B.25°
C.40°
D.50°
D
探索新知
如图,连接OA,根据切线的性质,先求出∠OAC=90°,再根据等腰三角形的性质和∠B=20°,可以求出∠AOC=40°,最后根据直角三角形中两锐角互余就可以求出∠C=50°. 答案:D
导引:
探索新知
总 结
(1)半径处处相等可得等腰三角形,从而底角相等;
(2)切线垂直于过切点的半径得直角三角形,从而两锐角互余.
典题精讲
下列说法正确的是( )
A.圆的切线垂直于半径
B.垂直于切线的直线经过圆心
C.经过圆心且垂直于切线的直线经过切点
D.经过切点的直线经过圆心
1
C
典题精讲
如图,直线l 是⊙O 的切线,A 为切点,B 为直线l 上一点,连接OB 交⊙O 于点C. 若AB=12,OA=5,则BC 的长为( )
A.5
B.6
C.7
D.8
2
D
典题精讲
如图,AB 是⊙O 的直径,AC 切⊙O 于点A,BC 交⊙O 于点D,若∠C=70°,则∠AOD 的度数为( )
A.70°
B.35°
C.20°
D.40°
3
D
典题精讲
如图,⊙O 是Rt△ABC 的外接圆,∠ACB=90°,∠A=25°,过点C 作⊙O 的切线,交AB 的延长线于点D,则∠D 的度数是( )
A.25°
B.40°
C.50°
D.65°
4
B
探索新知
2
知识点
切线性质定理的应用
例2 如图,△ABC 内接于⊙O,AB 是⊙O 的直径,∠BAC=2∠B,
⊙O 的切线AP 与OC 的延长线 相交于点P,若PA=6 cm,
求AC 的长.
探索新知
根据AB 是⊙O 的直径求出∠ACB=90°,再根据∠BAC=2∠B 求出∠B=30°,∠BAC=60°,得出△AOC 是等边三角形,得出∠AOC=60°,OA=AC,在Rt△OAP 中,求出OA,即可求出AC 的长.
导引:
探索新知
∵AB 是⊙O 的直径,∴∠ACB=90°.
又∵∠BAC=2∠B,∴∠B=30°,∠BAC=60°.
又∵OA=OC,∴△AOC 是等边三角形,
∴∠AOC=60°,AC=OA.
∵PA 是⊙O 的切线,∴∠OAP=90°.
在Rt△OAP 中,∵PA=6 cm,∠AOP=60°,
∴OA= =6(cm),
∴AC=OA=6 cm.
解:
探索新知
如图,在△ABC 中,AB=1,AC= ,点O 在AB 的延长线上,AC 切⊙O 于点C. 求:
(1)⊙O 的半径;
(2)∠A 的度数.
例3
连接OC,易得Rt△OAC,运用勾股定理求⊙O 的半径.在Rt△OAC 中,利用锐角三角函数求∠A 的度数.
导引:
探索新知
(1)连接OC.
∵AC 切⊙O于点C,∴OC⊥AC,
设⊙O 的半径为r,则OC=OB=r.
∴OA=OB+AB=1+r.
在Rt△OAC 中,OA2=OC 2+AC 2,
即(1+r )2=r 2+( )2,解得r=1.故⊙O 的半径为1.
(2)由(1)得OC=1,OA=2.
在Rt△OAC 中,sin A= ,∴∠A=30°.
解:
探索新知
总 结
当圆中有切线和切点时,通常连接过切点的半径,则这条半径必与切线垂直,本例中作辅助线的方法,适用于同类条件下与圆有关的求值或证明题.
典题精讲
如图,一枚直径为d 的硬币沿着直线滚动一圈,圆心经过的距离是多少?
1
解:πd.
典题精讲
如图,以点O 为圆心的两个圆中,大圆的弦AB 切小圆于点C,OA 交小圆于点D,若OD=2,tan ∠OAB= ,则AB 的长是( )
A.4
B.2
C.8
D.4
2
C
典题精讲
如图,菱形ABCD 的边AB=20,面积为320,∠BAD<90°,⊙O 与边AB,AD 都相切,AO=10,则⊙O 的半径长等于( )
A.5
B.6
C.2
D.3
3
C
典题精讲
如图,在平面直角坐标系中,点P 在第一象限内,x 轴与⊙P 相切于点Q,y 轴与⊙P 相交于M (0,2),N (0,8)两点,则点P 的坐标是( )
A.(5,3)
B.(3,5)
C.(5,4)
D.(4,5)
4
D
典题精讲
如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C 落在直尺的10 cm处,铁片与直尺的唯一公共点A 落在直尺的14 cm处,铁片与三角尺的唯一公共点为B.下列说法错误的是( )
A.圆形铁片的半径是4 cm
B.四边形AOBC 为正方形
C.弧AB 的长度为4π cm
D.扇形OAB 的面积是4π cm2
5
C
易错提醒
如图,△ABC 中,AB=5,BC=3,AC=4,以点C 为圆心的圆与AB 相切,则⊙C 的半径为( )
A.2.3 B.2.4
C.2.5 D.2.6
易错点:忽视“过切点”这一条件而致错.
B
学以致用
小试牛刀
如图,AB 是⊙O 的直径,点C 为⊙O 外一点,CA,CD 是⊙O 的切线,A,D 为切点,连接BD,AD.若∠ACD=30°,则∠DBA 的大小是( )
A.15°
B.30°
C.60°
D.75°
1
B
小试牛刀
如图,圆内接四边形ABCD 的边AB 过圆心O,过点C 的切线与边AD 所在直线垂直于点M,若∠ABC=55°,则∠ACD 等于( )
A.20°
B.35°
C.40°
D.55°
2
A
小试牛刀
3 如图,已知AB 是⊙O 的直径,CD 与⊙O 相切于C,BE∥CO.
(1)求证:BC 是∠ABE 的平分线;
(2)若DC=8,⊙O 的半径OA=6,求CE 的长.
小试牛刀
∵DE 是⊙O 的切线,
∴OC⊥DE.
∵BE∥CO,
∴∠OCB=∠CBE.
∵OC=OB,
∴∠OCB=∠OBC.
∴∠CBE=∠OBC.
∴BC 平分∠ABE.
(1)证明:
在Rt△CDO 中,
∵DC=8,OC=OA=6,
∴OD=
∵OC∥BE,∴
∴
∴CE=4.8.
(2)解:
小试牛刀
4 如图,在△ABC 中,AC=BC,∠ACB=90°,⊙O (圆心O 在△ABC 内部)经过B,C 两点,交AB 于点E,过点E 作⊙O 的切线交AC 于点F. 延长CO 交AB 于点G,作ED∥AC 交CG 于点D.
(1)求证:四边形CDEF 是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG 的值.
小试牛刀
如图,连接CE.
∵在△ABC 中,AC=BC,∠ACB=90°,
∴∠B=45°.∴∠COE=90°.
∴∠CEO=∠ECO=45°.
∵EF 是⊙O 的切线,
∴∠FEO=90°. ∴∠FEC=45°.
∴∠FEC=∠ECO.∴EF∥CG.
又∵ED∥AC,
∴四边形CDEF 是平行四边形.
(1)证明:
小试牛刀
如图,过G 作GM⊥BC于M,
∴△GMB 是等腰直角三角形,∴MB=GM.
∵四边形CDEF 是平行四边形,
∴∠FCD=∠FED.
∵∠ACD+∠GCB=∠GCB+∠CGM=90°,
∴∠CGM=∠ACD.∴∠CGM=∠DEF.
∵tan∠DEF=2,∴tan∠CGM=
∴CM=2GM,
又∵BC=CM+BM=2GM+GM=3,
∴GM=1.∴BG= GM=
(2)解:
小试牛刀
5 如图,AB 是⊙O 的直径,∠BAC=90°,四边形EBOC 是平行四边形,EB 交⊙O 于点D,连接CD 并延长交AB 的延长线于点F.
(1)求证:CF 是⊙O 的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π).
小试牛刀
如图,连接OD.∵四边形EBOC 是平行四边形,
∴OC∥BE.∴∠AOC=∠OBE,∠COD=∠ODB.
∵OB=OD,∴∠OBD=∠ODB.∴∠DOC=∠AOC.
在△COD 和△COA 中,
OC=OC,
∠COD=∠COA,
OD=OA,
∴△COD ≌ △COA.
(1)证明:
小试牛刀
∴∠CDO=∠CAO=90°.
∴圆心O 到CF 的距离等于⊙O 的半径.
∴CF 是⊙O 的切线.
小试牛刀
∵∠F=30°,∠ODF=90°,
∴∠DOF=60°,∴∠AOD=120°.
∵OD=OB,∴△OBD 是等边三角形,
∴∠BDO=∠DBO=60°,OB=BD.
易得∠EDC=∠ECD=30°,
∴ED=EC.
∵四边形EBOC 是平行四边形,
∴EC=ED=BO=DB.
∵EB=4,∴OB=OD=OA=2.
(2)解:
小试牛刀
∵∠AOC=∠COD,∴∠AOC=60°.
在Rt△AOC 中,∵∠OAC=90°,∠AOC=60°,
∴∠OCA=30°.∵OA=2,∴OC=4.
∴AC=
∴S阴影=2S△AOC-S扇形OAD
=
小试牛刀
6 已知AB 是⊙O 的直径,AT 是⊙O 的切线,∠ABT=50°,BT交⊙O 于点C,E 是AB 上一点,延长CE 交⊙O 于点D.
(1)如图①,求∠T 和∠CDB 的大小;
(2)如图②,当BE=BC 时,求∠CDO 的大小.
小试牛刀
(1)如图①,连接AC,
∵AT 是⊙O 的切线,AB 是⊙O 的直径,
∴∠TAB=90°.
∵∠ABT=50°,
∴∠T=90°-∠ABT=40°.
由AB 是⊙O 的直径,得∠ACB=90°.
∴∠CAB=90°-∠ABC=40°.
∴∠CDB=∠CAB=40°.
解:
小试牛刀
(2)如图②,连接AD,
在△BCE 中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°.
∴∠BAD=∠BCD=65°.
∵OA=OD,
∴∠ODA=∠OAD=65°.
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA-∠ADC=65°-50°=15°.
课堂小结
课堂小结
圆的切线垂直于过切点的半径. 已知直线满足:
(1)过圆心;
(2)过切点;
(3)垂直于直线任意两个,就可得到第三个.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6 直线和圆的位置关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
前一节课已经学到点和圆的位置关系.设⊙O 的
半径为r,点P 到圆心的距离OP =d,
则有:点P 在圆外 d>r,如图(a)所示;
点P 在圆上 d=r,如图(b)所示;
点P 在圆内 d
探索新知
1
知识点
切线的性质定理
前面我们已学过的切线的性质有哪些?
答:①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
切线还有什么性质?
切线的性质定理:圆的切线垂直于过切点的半径.
探索新知
例1 如图,AB 是⊙O 的弦,AC 是⊙O 的切线,A 为切点
BC 经过圆心.若∠B=20°,则∠C 的大小为( )
A.20°
B.25°
C.40°
D.50°
D
探索新知
如图,连接OA,根据切线的性质,先求出∠OAC=90°,再根据等腰三角形的性质和∠B=20°,可以求出∠AOC=40°,最后根据直角三角形中两锐角互余就可以求出∠C=50°. 答案:D
导引:
探索新知
总 结
(1)半径处处相等可得等腰三角形,从而底角相等;
(2)切线垂直于过切点的半径得直角三角形,从而两锐角互余.
典题精讲
下列说法正确的是( )
A.圆的切线垂直于半径
B.垂直于切线的直线经过圆心
C.经过圆心且垂直于切线的直线经过切点
D.经过切点的直线经过圆心
1
C
典题精讲
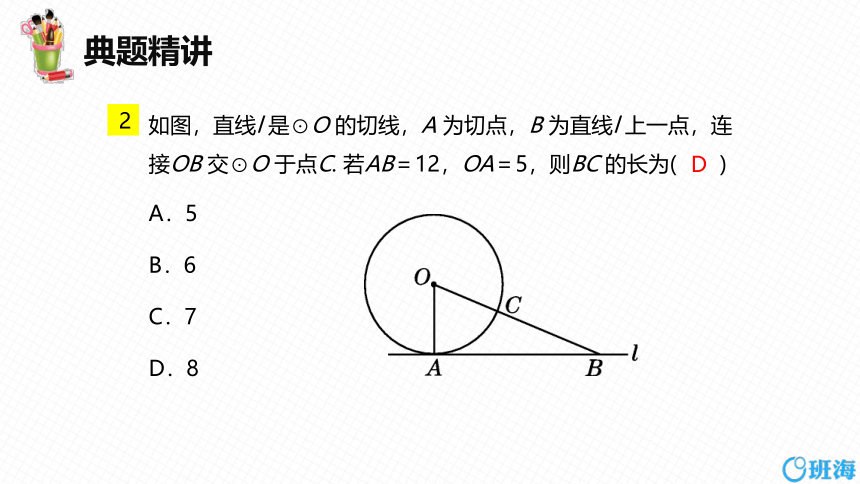
如图,直线l 是⊙O 的切线,A 为切点,B 为直线l 上一点,连接OB 交⊙O 于点C. 若AB=12,OA=5,则BC 的长为( )
A.5
B.6
C.7
D.8
2
D
典题精讲
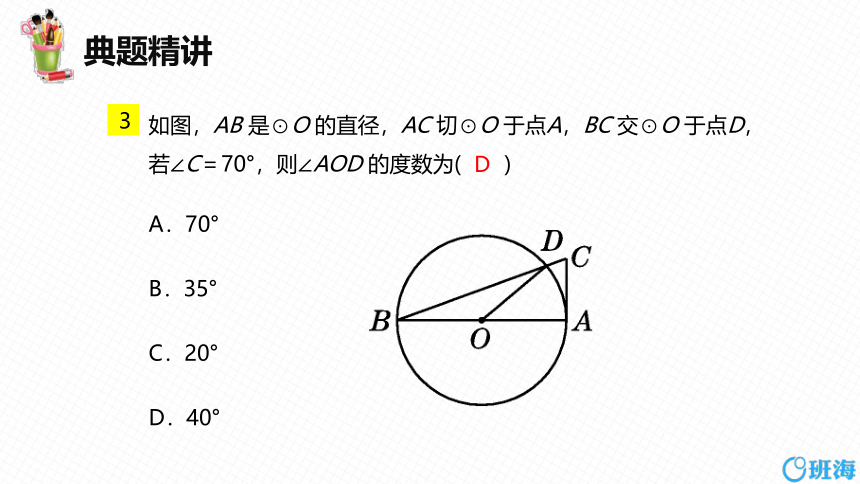
如图,AB 是⊙O 的直径,AC 切⊙O 于点A,BC 交⊙O 于点D,若∠C=70°,则∠AOD 的度数为( )
A.70°
B.35°
C.20°
D.40°
3
D
典题精讲
如图,⊙O 是Rt△ABC 的外接圆,∠ACB=90°,∠A=25°,过点C 作⊙O 的切线,交AB 的延长线于点D,则∠D 的度数是( )
A.25°
B.40°
C.50°
D.65°
4
B
探索新知
2
知识点
切线性质定理的应用
例2 如图,△ABC 内接于⊙O,AB 是⊙O 的直径,∠BAC=2∠B,
⊙O 的切线AP 与OC 的延长线 相交于点P,若PA=6 cm,
求AC 的长.
探索新知
根据AB 是⊙O 的直径求出∠ACB=90°,再根据∠BAC=2∠B 求出∠B=30°,∠BAC=60°,得出△AOC 是等边三角形,得出∠AOC=60°,OA=AC,在Rt△OAP 中,求出OA,即可求出AC 的长.
导引:
探索新知
∵AB 是⊙O 的直径,∴∠ACB=90°.
又∵∠BAC=2∠B,∴∠B=30°,∠BAC=60°.
又∵OA=OC,∴△AOC 是等边三角形,
∴∠AOC=60°,AC=OA.
∵PA 是⊙O 的切线,∴∠OAP=90°.
在Rt△OAP 中,∵PA=6 cm,∠AOP=60°,
∴OA= =6(cm),
∴AC=OA=6 cm.
解:
探索新知
如图,在△ABC 中,AB=1,AC= ,点O 在AB 的延长线上,AC 切⊙O 于点C. 求:
(1)⊙O 的半径;
(2)∠A 的度数.
例3
连接OC,易得Rt△OAC,运用勾股定理求⊙O 的半径.在Rt△OAC 中,利用锐角三角函数求∠A 的度数.
导引:
探索新知
(1)连接OC.
∵AC 切⊙O于点C,∴OC⊥AC,
设⊙O 的半径为r,则OC=OB=r.
∴OA=OB+AB=1+r.
在Rt△OAC 中,OA2=OC 2+AC 2,
即(1+r )2=r 2+( )2,解得r=1.故⊙O 的半径为1.
(2)由(1)得OC=1,OA=2.
在Rt△OAC 中,sin A= ,∴∠A=30°.
解:
探索新知
总 结
当圆中有切线和切点时,通常连接过切点的半径,则这条半径必与切线垂直,本例中作辅助线的方法,适用于同类条件下与圆有关的求值或证明题.
典题精讲
如图,一枚直径为d 的硬币沿着直线滚动一圈,圆心经过的距离是多少?
1
解:πd.
典题精讲
如图,以点O 为圆心的两个圆中,大圆的弦AB 切小圆于点C,OA 交小圆于点D,若OD=2,tan ∠OAB= ,则AB 的长是( )
A.4
B.2
C.8
D.4
2
C
典题精讲
如图,菱形ABCD 的边AB=20,面积为320,∠BAD<90°,⊙O 与边AB,AD 都相切,AO=10,则⊙O 的半径长等于( )
A.5
B.6
C.2
D.3
3
C
典题精讲
如图,在平面直角坐标系中,点P 在第一象限内,x 轴与⊙P 相切于点Q,y 轴与⊙P 相交于M (0,2),N (0,8)两点,则点P 的坐标是( )
A.(5,3)
B.(3,5)
C.(5,4)
D.(4,5)
4
D
典题精讲
如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C 落在直尺的10 cm处,铁片与直尺的唯一公共点A 落在直尺的14 cm处,铁片与三角尺的唯一公共点为B.下列说法错误的是( )
A.圆形铁片的半径是4 cm
B.四边形AOBC 为正方形
C.弧AB 的长度为4π cm
D.扇形OAB 的面积是4π cm2
5
C
易错提醒
如图,△ABC 中,AB=5,BC=3,AC=4,以点C 为圆心的圆与AB 相切,则⊙C 的半径为( )
A.2.3 B.2.4
C.2.5 D.2.6
易错点:忽视“过切点”这一条件而致错.
B
学以致用
小试牛刀
如图,AB 是⊙O 的直径,点C 为⊙O 外一点,CA,CD 是⊙O 的切线,A,D 为切点,连接BD,AD.若∠ACD=30°,则∠DBA 的大小是( )
A.15°
B.30°
C.60°
D.75°
1
B
小试牛刀
如图,圆内接四边形ABCD 的边AB 过圆心O,过点C 的切线与边AD 所在直线垂直于点M,若∠ABC=55°,则∠ACD 等于( )
A.20°
B.35°
C.40°
D.55°
2
A
小试牛刀
3 如图,已知AB 是⊙O 的直径,CD 与⊙O 相切于C,BE∥CO.
(1)求证:BC 是∠ABE 的平分线;
(2)若DC=8,⊙O 的半径OA=6,求CE 的长.
小试牛刀
∵DE 是⊙O 的切线,
∴OC⊥DE.
∵BE∥CO,
∴∠OCB=∠CBE.
∵OC=OB,
∴∠OCB=∠OBC.
∴∠CBE=∠OBC.
∴BC 平分∠ABE.
(1)证明:
在Rt△CDO 中,
∵DC=8,OC=OA=6,
∴OD=
∵OC∥BE,∴
∴
∴CE=4.8.
(2)解:
小试牛刀
4 如图,在△ABC 中,AC=BC,∠ACB=90°,⊙O (圆心O 在△ABC 内部)经过B,C 两点,交AB 于点E,过点E 作⊙O 的切线交AC 于点F. 延长CO 交AB 于点G,作ED∥AC 交CG 于点D.
(1)求证:四边形CDEF 是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG 的值.
小试牛刀
如图,连接CE.
∵在△ABC 中,AC=BC,∠ACB=90°,
∴∠B=45°.∴∠COE=90°.
∴∠CEO=∠ECO=45°.
∵EF 是⊙O 的切线,
∴∠FEO=90°. ∴∠FEC=45°.
∴∠FEC=∠ECO.∴EF∥CG.
又∵ED∥AC,
∴四边形CDEF 是平行四边形.
(1)证明:
小试牛刀
如图,过G 作GM⊥BC于M,
∴△GMB 是等腰直角三角形,∴MB=GM.
∵四边形CDEF 是平行四边形,
∴∠FCD=∠FED.
∵∠ACD+∠GCB=∠GCB+∠CGM=90°,
∴∠CGM=∠ACD.∴∠CGM=∠DEF.
∵tan∠DEF=2,∴tan∠CGM=
∴CM=2GM,
又∵BC=CM+BM=2GM+GM=3,
∴GM=1.∴BG= GM=
(2)解:
小试牛刀
5 如图,AB 是⊙O 的直径,∠BAC=90°,四边形EBOC 是平行四边形,EB 交⊙O 于点D,连接CD 并延长交AB 的延长线于点F.
(1)求证:CF 是⊙O 的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π).
小试牛刀
如图,连接OD.∵四边形EBOC 是平行四边形,
∴OC∥BE.∴∠AOC=∠OBE,∠COD=∠ODB.
∵OB=OD,∴∠OBD=∠ODB.∴∠DOC=∠AOC.
在△COD 和△COA 中,
OC=OC,
∠COD=∠COA,
OD=OA,
∴△COD ≌ △COA.
(1)证明:
小试牛刀
∴∠CDO=∠CAO=90°.
∴圆心O 到CF 的距离等于⊙O 的半径.
∴CF 是⊙O 的切线.
小试牛刀
∵∠F=30°,∠ODF=90°,
∴∠DOF=60°,∴∠AOD=120°.
∵OD=OB,∴△OBD 是等边三角形,
∴∠BDO=∠DBO=60°,OB=BD.
易得∠EDC=∠ECD=30°,
∴ED=EC.
∵四边形EBOC 是平行四边形,
∴EC=ED=BO=DB.
∵EB=4,∴OB=OD=OA=2.
(2)解:
小试牛刀
∵∠AOC=∠COD,∴∠AOC=60°.
在Rt△AOC 中,∵∠OAC=90°,∠AOC=60°,
∴∠OCA=30°.∵OA=2,∴OC=4.
∴AC=
∴S阴影=2S△AOC-S扇形OAD
=
小试牛刀
6 已知AB 是⊙O 的直径,AT 是⊙O 的切线,∠ABT=50°,BT交⊙O 于点C,E 是AB 上一点,延长CE 交⊙O 于点D.
(1)如图①,求∠T 和∠CDB 的大小;
(2)如图②,当BE=BC 时,求∠CDO 的大小.
小试牛刀
(1)如图①,连接AC,
∵AT 是⊙O 的切线,AB 是⊙O 的直径,
∴∠TAB=90°.
∵∠ABT=50°,
∴∠T=90°-∠ABT=40°.
由AB 是⊙O 的直径,得∠ACB=90°.
∴∠CAB=90°-∠ABC=40°.
∴∠CDB=∠CAB=40°.
解:
小试牛刀
(2)如图②,连接AD,
在△BCE 中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°.
∴∠BAD=∠BCD=65°.
∵OA=OD,
∴∠ODA=∠OAD=65°.
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA-∠ADC=65°-50°=15°.
课堂小结
课堂小结
圆的切线垂直于过切点的半径. 已知直线满足:
(1)过圆心;
(2)过切点;
(3)垂直于直线任意两个,就可得到第三个.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
