【班海精品】北师大版(新)九年级下-1.2 30°,45°,60°角的三角函数值 【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-1.2 30°,45°,60°角的三角函数值 【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览








文档简介
(共43张PPT)
2 30°,45°,60°角的三角函数值
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
观察一副三角尺,其中有几个锐角?它们分别等于多少度?
(1) sin 30°等于多少?你是怎样得到的?与同伴进行交流.
(2) cos 30°等于多少?tan 30° 呢?
情景导入
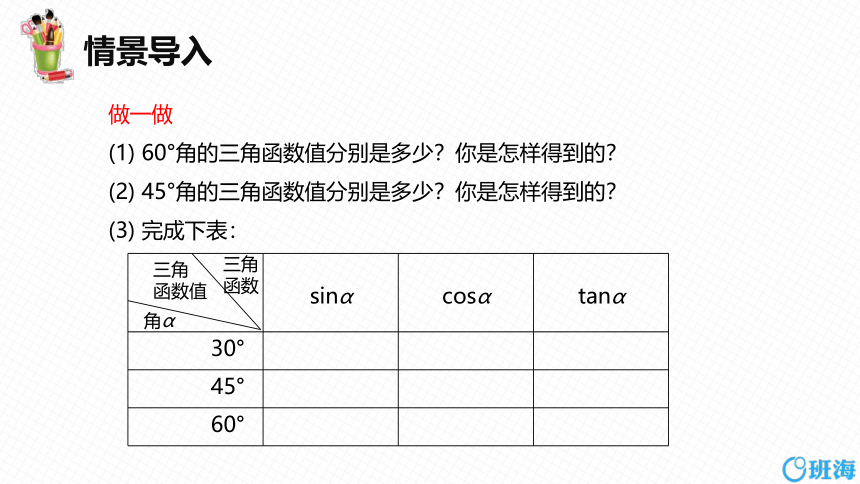
做一做
(1) 60°角的三角函数值分别是多少?你是怎样得到的?
(2) 45°角的三角函数值分别是多少?你是怎样得到的?
(3) 完成下表:
sinα cosα
tanα
30°
45°
60°
三角
函数
角α
三角
函数值
新课精讲
30° 45° 60°
sin α
cos α
tan α 1
探索新知
1
知识点
30°,45°,60°角的三角函数值
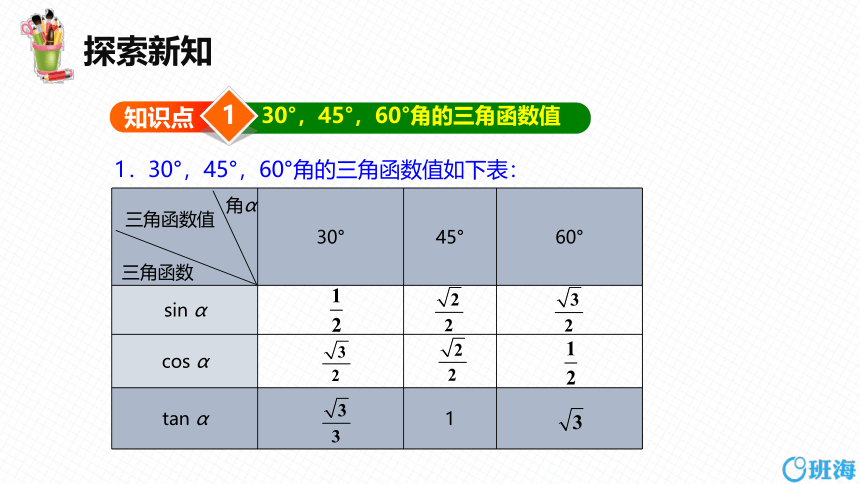
1.30°,45°,60°角的三角函数值如下表:
角α
三角函数值
三角函数
探索新知
例1 计算:
(1)sin 30° + cos 45° ;
(2) sin260°+ cos260° - tan 45°.
(1) sin 30° + cos 45° =
(2) sin260° + cos260° - tan 45°
解:
典题精讲
在△ABC 中,∠C=90°,sinA= BC = 20,
求△ABC 的周长和面积.
在Rt△ABC 中,∵sin A= ,BC=20,
∴AB= = =25.
∴由勾股定理得AC= = =15.
∴C△ABC=AB+BC+CA=25+20+15=60, S△ABC= BC·AC= ×20×15=150.
解:
典题精讲
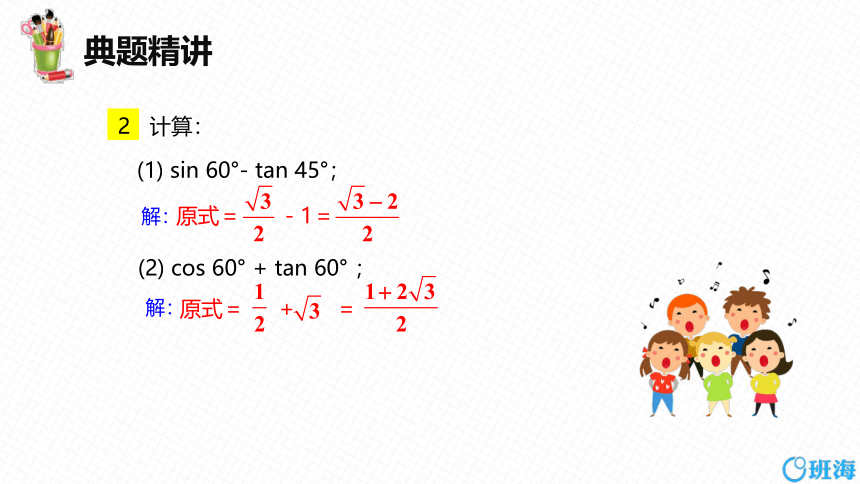
2 计算:
(1) sin 60°- tan 45°;
(2) cos 60° + tan 60° ;
原式= -1=
解:
解:
原式= + =
典题精讲
(3) sin 45° + sin 60° -2 cos 45°.
解:
原式= × + -2 ×
= + -
= .
典题精讲
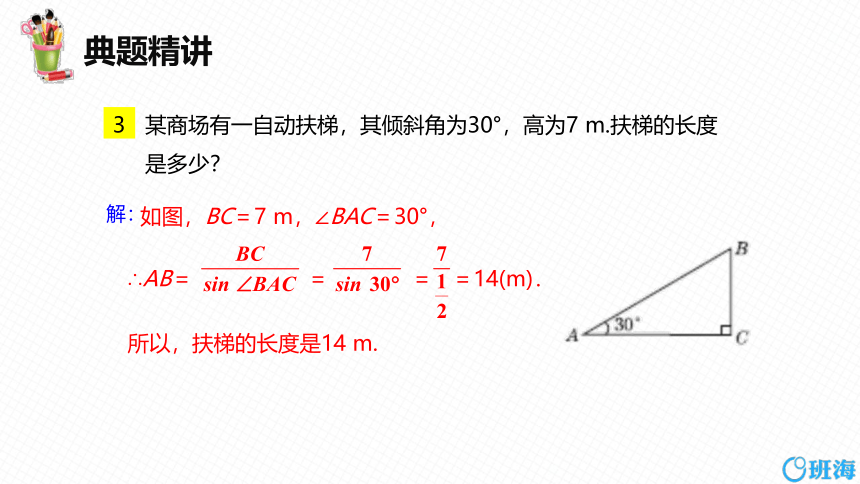
3 某商场有一自动扶梯,其倾斜角为30°,高为7 m.扶梯的长度是多少?
如图,BC=7 m,∠BAC=30°,
∴AB= = = =14(m).
所以,扶梯的长度是14 m.
解:
典题精讲
cos60° 的值等于( )
A. B. 1 C. D.
下列运算:sin 30°= , =2 ,π0=π,2-2=-4,其中运算结果正确的个数为( )
A.4 B.3 C.2 D.1
4
5
D
D
探索新知
2
知识点
由特殊三角函数值求角
通过该表可以方便地知道30°,45°,60°角的三角函数值.它的另一个应用:如果已知一个锐角的三角函数值,就可以求出这个锐角的度数.例如:若sin θ= ,则锐角θ=45°.
探索新知
在Rt△ABC 中,∠C =90°,BC = , AC= ,求∠A、∠B 的度数.
∵tanA=
∴∠A=30°,∠B=60°.
探索新知
例2 在Rt△ABC 中,∠C=90°,cos A= 求∠A,
∠B 的度数.
导引:利用特殊角的三角函数值,查找值所对应的角,再
利用直角三角形两锐角互余的性质求出∠B.
解:∵cos A= cos 30°=
∴∠A=30°.
∴∠B=90°-30°=60°.
探索新知
总 结
在运用数形结合记忆法或增减规律记忆法记住特殊角的三角函数值后,很容易确定∠A 的度数,从而可用两锐角互余的关系计算∠B.
典题精讲
在等腰三角形ABC 中,AB=AC=5,BC=6,求sinB , cosB,tanB.
过点A 作AD⊥BC 于点D.
∵△ABC 是等腰三角形,
∴BD=CD= BC=3.
在Rt△ABD 中,∵AD= =4,
∴sin B= = ,cos B= = ,
tan B= = .
解:
典题精讲
在△ABC 中,若角A,B 满足|cos A- |+(1-tan B )2=0,则∠C 的大小是( )
A.45° B.60°
C.75° D.105°
D
在△ABC 中,∠A,∠B 都是锐角,且sin A= ,cos B= ,则△ABC 的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
3
B
典题精讲
若( tan A-1)2+|2cos B- |=0,则△ABC
是( )
A.直角三角形
B.含有60°角的任意三角形
C.等边三角形
D.顶角为钝角的等腰三角形
4
D
探索新知
3
知识点
同角(余角)三角函数间的关系
如图,在Rt△ABC 中,∠C=90°,∠A,∠B,
∠C 的对边分别为a,b,c,令∠A=α.
(1)同角三角函数之间的关系.
①平方关系:sin2 α+cos2 α=1.
②商关系:∵
且tan α= ∴ =tan α.
探索新知
(2)互余两角的三角函数的关系.
sin A=cos B.同理cos A=sin B.
即任意锐角的正弦值等于它的余角的余弦值,
任意锐角的余弦值等于它的余角的正弦值.
∵tan A= tan B=
∴tan A·tan B=1.
此结论适用于两个角互为余角的情况.
探索新知
例3 已知α 为锐角,且cos α= 求 的值.
运用同角三角函数的关系,由cos α 的值可求得sin α
及tan α 的值,然后代入计算即可.
导引:
探索新知
由sin2α+cos2α=1,sin α>0,得sin α=
而cos α= 所以sin α=
因为 =tan α,所以tan α=
故
解:
典题精讲
已知α 为锐角,m=sin2α+cos2α,则( )
A.m>1 B.m=1 C.m<1 D.m≥1
在Rt△ABC 中,∠C=90°,若cos B= 则sin B
的值是( )
A. B. C. D.
B
A
典题精讲
3 在Rt△ABC 中,∠C=90°,sin B= 则cos A
的值为( )
A. B. C. D.
C
已知α,β 都是锐角,如果sin α=cos β,那么α 与β 之间满足的关系是( )
A.α=β B.α+β=90°
C.α-β=90° D.β-α=90°
4
B
易错提醒
如图,在△ABC 中,AC=1,AB=2,∠A=60°,求BC 的长.
易错点:忽视锐角的三角函数值应在直角三角形中求解这一
条件而致错.
易错提醒
在△ABC 中,∵ =sin A,∴BC=AB sin A=2sin 60°=2× =3.
错解的原因是忽略了锐角三角函数使用的前提是在直角三角形中.本题中没有明确指出△ABC 是直角三角形,因此,不能直接得到 =sin A,必须通过添加辅助线,构造出直角三角形,再利用三角函数的定义来解决.
如图,过点C 作CD⊥AB 于点D.
错解:
诊断:
正解:
易错提醒
在Rt△ADC 中,∵cos A= ,sin A= ,
∴AD=AC cos A=1×cos 60°= ,
CD=AC sin A=1×sin 60°= .
在Rt△BDC 中,BD=AB-AD=2-
∴BC=
学以致用
小试牛刀
计算sin245°+cos 30°·tan 60°,其结果是( )
A.2 B.1 C. D.
1
A
菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC=45°,OC= ,则点B 的坐标为( )
A.( ,1)
B.(1, )
C.( +1,1)
D.(1, +1)
2
C
小试牛刀
将宽为2 cm的长方形纸条折叠成如图所示的形状,那么折痕PQ 的长是( )
A. cm
B. cm
C. cm
D.2 cm
3
B
小试牛刀
4 (1)计算:
(2)先化简,再求值:
其中x=2(tan 45°-cos 30°).
小试牛刀
(1)原式=4-1+2- +4× =5-
(2)原式=
=
∵x=2(tan 45°-cos 30°)
=
∴
解:
小试牛刀
5 如图,在△ABC 中,∠C=90°,点D 在AC 上,已知∠BDC=45°,BD= ,AB=20.求∠A 的度数.
小试牛刀
∵∠BDC=45°,∠C=90°,
∴△BCD 为等腰直角三角形.
∴BC=CD.
又∵BD= ,∴BC=10.
又∵AB=20,∴sin A=
∴∠A=30°.
解:
小试牛刀
某地的一座人行天桥如图所示,天桥高为6 m,坡面BC 的坡
度为1∶1,为了方便行人推车过天桥,有关部门决定降低坡
度,使新坡面的坡度为1∶
(1)求新坡面的坡角α.
(2)原天桥底部正前方8 m处(PB 的长)的文化墙PM 是否需要拆除?请说明理由.
小试牛刀
(1)∵新坡面的坡度为1∶
∴tan α=tan ∠CAB=
∴α=30°.
答:新坡面的坡角α 为30°.
(2)文化墙PM 不需要拆除.
如图,过点C 作CD⊥AB 于点D,则CD=6.
∵坡面BC 的坡度为1∶1,新坡面的坡度为1∶
∴BD=CD=6 m,AD=
∴AB=AD-BD=( -6)m<8 m.
∴文化墙PM 不需要拆除.
解:
小试牛刀
7 要求tan 30°的值,可构造如图所示的直角三角形进行计算:在Rt△ABC 中,使∠C=90°,斜边AB=2,直角边AC =1,那么 BC= ,∠ABC=30°,∴tan 30°= 在此图的基础上,通过添加适当的辅助线,可求出tan 15°的值,请画出你添加的辅助线,并求出tan 15°的值.
小试牛刀
图略.延长CB 至点D,使BD=AB,连接AD,则∠D=15°,tan 15°=
解:
课堂小结
课堂小结
30° 45° 60°
sin A
cos A
tan A 1
特殊角的三角函数值:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2 30°,45°,60°角的三角函数值
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
观察一副三角尺,其中有几个锐角?它们分别等于多少度?
(1) sin 30°等于多少?你是怎样得到的?与同伴进行交流.
(2) cos 30°等于多少?tan 30° 呢?
情景导入
做一做
(1) 60°角的三角函数值分别是多少?你是怎样得到的?
(2) 45°角的三角函数值分别是多少?你是怎样得到的?
(3) 完成下表:
sinα cosα
tanα
30°
45°
60°
三角
函数
角α
三角
函数值
新课精讲
30° 45° 60°
sin α
cos α
tan α 1
探索新知
1
知识点
30°,45°,60°角的三角函数值
1.30°,45°,60°角的三角函数值如下表:
角α
三角函数值
三角函数
探索新知
例1 计算:
(1)sin 30° + cos 45° ;
(2) sin260°+ cos260° - tan 45°.
(1) sin 30° + cos 45° =
(2) sin260° + cos260° - tan 45°
解:
典题精讲
在△ABC 中,∠C=90°,sinA= BC = 20,
求△ABC 的周长和面积.
在Rt△ABC 中,∵sin A= ,BC=20,
∴AB= = =25.
∴由勾股定理得AC= = =15.
∴C△ABC=AB+BC+CA=25+20+15=60, S△ABC= BC·AC= ×20×15=150.
解:
典题精讲
2 计算:
(1) sin 60°- tan 45°;
(2) cos 60° + tan 60° ;
原式= -1=
解:
解:
原式= + =
典题精讲
(3) sin 45° + sin 60° -2 cos 45°.
解:
原式= × + -2 ×
= + -
= .
典题精讲
3 某商场有一自动扶梯,其倾斜角为30°,高为7 m.扶梯的长度是多少?
如图,BC=7 m,∠BAC=30°,
∴AB= = = =14(m).
所以,扶梯的长度是14 m.
解:
典题精讲
cos60° 的值等于( )
A. B. 1 C. D.
下列运算:sin 30°= , =2 ,π0=π,2-2=-4,其中运算结果正确的个数为( )
A.4 B.3 C.2 D.1
4
5
D
D
探索新知
2
知识点
由特殊三角函数值求角
通过该表可以方便地知道30°,45°,60°角的三角函数值.它的另一个应用:如果已知一个锐角的三角函数值,就可以求出这个锐角的度数.例如:若sin θ= ,则锐角θ=45°.
探索新知
在Rt△ABC 中,∠C =90°,BC = , AC= ,求∠A、∠B 的度数.
∵tanA=
∴∠A=30°,∠B=60°.
探索新知
例2 在Rt△ABC 中,∠C=90°,cos A= 求∠A,
∠B 的度数.
导引:利用特殊角的三角函数值,查找值所对应的角,再
利用直角三角形两锐角互余的性质求出∠B.
解:∵cos A= cos 30°=
∴∠A=30°.
∴∠B=90°-30°=60°.
探索新知
总 结
在运用数形结合记忆法或增减规律记忆法记住特殊角的三角函数值后,很容易确定∠A 的度数,从而可用两锐角互余的关系计算∠B.
典题精讲
在等腰三角形ABC 中,AB=AC=5,BC=6,求sinB , cosB,tanB.
过点A 作AD⊥BC 于点D.
∵△ABC 是等腰三角形,
∴BD=CD= BC=3.
在Rt△ABD 中,∵AD= =4,
∴sin B= = ,cos B= = ,
tan B= = .
解:
典题精讲
在△ABC 中,若角A,B 满足|cos A- |+(1-tan B )2=0,则∠C 的大小是( )
A.45° B.60°
C.75° D.105°
D
在△ABC 中,∠A,∠B 都是锐角,且sin A= ,cos B= ,则△ABC 的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
3
B
典题精讲
若( tan A-1)2+|2cos B- |=0,则△ABC
是( )
A.直角三角形
B.含有60°角的任意三角形
C.等边三角形
D.顶角为钝角的等腰三角形
4
D
探索新知
3
知识点
同角(余角)三角函数间的关系
如图,在Rt△ABC 中,∠C=90°,∠A,∠B,
∠C 的对边分别为a,b,c,令∠A=α.
(1)同角三角函数之间的关系.
①平方关系:sin2 α+cos2 α=1.
②商关系:∵
且tan α= ∴ =tan α.
探索新知
(2)互余两角的三角函数的关系.
sin A=cos B.同理cos A=sin B.
即任意锐角的正弦值等于它的余角的余弦值,
任意锐角的余弦值等于它的余角的正弦值.
∵tan A= tan B=
∴tan A·tan B=1.
此结论适用于两个角互为余角的情况.
探索新知
例3 已知α 为锐角,且cos α= 求 的值.
运用同角三角函数的关系,由cos α 的值可求得sin α
及tan α 的值,然后代入计算即可.
导引:
探索新知
由sin2α+cos2α=1,sin α>0,得sin α=
而cos α= 所以sin α=
因为 =tan α,所以tan α=
故
解:
典题精讲
已知α 为锐角,m=sin2α+cos2α,则( )
A.m>1 B.m=1 C.m<1 D.m≥1
在Rt△ABC 中,∠C=90°,若cos B= 则sin B
的值是( )
A. B. C. D.
B
A
典题精讲
3 在Rt△ABC 中,∠C=90°,sin B= 则cos A
的值为( )
A. B. C. D.
C
已知α,β 都是锐角,如果sin α=cos β,那么α 与β 之间满足的关系是( )
A.α=β B.α+β=90°
C.α-β=90° D.β-α=90°
4
B
易错提醒
如图,在△ABC 中,AC=1,AB=2,∠A=60°,求BC 的长.
易错点:忽视锐角的三角函数值应在直角三角形中求解这一
条件而致错.
易错提醒
在△ABC 中,∵ =sin A,∴BC=AB sin A=2sin 60°=2× =3.
错解的原因是忽略了锐角三角函数使用的前提是在直角三角形中.本题中没有明确指出△ABC 是直角三角形,因此,不能直接得到 =sin A,必须通过添加辅助线,构造出直角三角形,再利用三角函数的定义来解决.
如图,过点C 作CD⊥AB 于点D.
错解:
诊断:
正解:
易错提醒
在Rt△ADC 中,∵cos A= ,sin A= ,
∴AD=AC cos A=1×cos 60°= ,
CD=AC sin A=1×sin 60°= .
在Rt△BDC 中,BD=AB-AD=2-
∴BC=
学以致用
小试牛刀
计算sin245°+cos 30°·tan 60°,其结果是( )
A.2 B.1 C. D.
1
A
菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC=45°,OC= ,则点B 的坐标为( )
A.( ,1)
B.(1, )
C.( +1,1)
D.(1, +1)
2
C
小试牛刀
将宽为2 cm的长方形纸条折叠成如图所示的形状,那么折痕PQ 的长是( )
A. cm
B. cm
C. cm
D.2 cm
3
B
小试牛刀
4 (1)计算:
(2)先化简,再求值:
其中x=2(tan 45°-cos 30°).
小试牛刀
(1)原式=4-1+2- +4× =5-
(2)原式=
=
∵x=2(tan 45°-cos 30°)
=
∴
解:
小试牛刀
5 如图,在△ABC 中,∠C=90°,点D 在AC 上,已知∠BDC=45°,BD= ,AB=20.求∠A 的度数.
小试牛刀
∵∠BDC=45°,∠C=90°,
∴△BCD 为等腰直角三角形.
∴BC=CD.
又∵BD= ,∴BC=10.
又∵AB=20,∴sin A=
∴∠A=30°.
解:
小试牛刀
某地的一座人行天桥如图所示,天桥高为6 m,坡面BC 的坡
度为1∶1,为了方便行人推车过天桥,有关部门决定降低坡
度,使新坡面的坡度为1∶
(1)求新坡面的坡角α.
(2)原天桥底部正前方8 m处(PB 的长)的文化墙PM 是否需要拆除?请说明理由.
小试牛刀
(1)∵新坡面的坡度为1∶
∴tan α=tan ∠CAB=
∴α=30°.
答:新坡面的坡角α 为30°.
(2)文化墙PM 不需要拆除.
如图,过点C 作CD⊥AB 于点D,则CD=6.
∵坡面BC 的坡度为1∶1,新坡面的坡度为1∶
∴BD=CD=6 m,AD=
∴AB=AD-BD=( -6)m<8 m.
∴文化墙PM 不需要拆除.
解:
小试牛刀
7 要求tan 30°的值,可构造如图所示的直角三角形进行计算:在Rt△ABC 中,使∠C=90°,斜边AB=2,直角边AC =1,那么 BC= ,∠ABC=30°,∴tan 30°= 在此图的基础上,通过添加适当的辅助线,可求出tan 15°的值,请画出你添加的辅助线,并求出tan 15°的值.
小试牛刀
图略.延长CB 至点D,使BD=AB,连接AD,则∠D=15°,tan 15°=
解:
课堂小结
课堂小结
30° 45° 60°
sin A
cos A
tan A 1
特殊角的三角函数值:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
