【班海精品】北师大版(新)九年级下-3.9弧长及扇形的面积【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-3.9弧长及扇形的面积【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览









文档简介
(共54张PPT)
9 弧长及扇形的面积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们在小学学习了圆的面积和扇形的面积,也学习了圆的周长,那么圆上一部分的长,也就是一条弧的长怎么去求呢?现在重新学习圆的面积和扇形面积,比以前是不是有了更深的要求呢?
下面我们就来学习本节内容.
新课精讲
探索新知
1
知识点
弧长公式
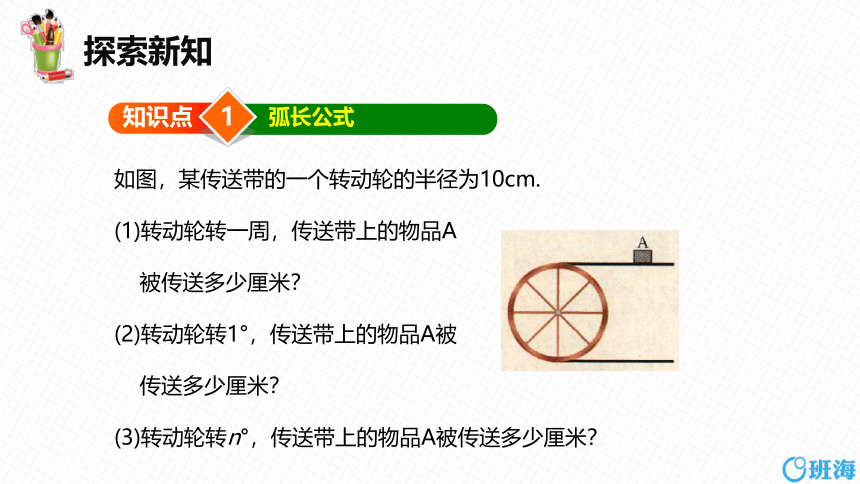
如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品A
被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被
传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
探索新知
归 纳
在半径为R 的圆中, n° 的圆心角所对的弧长的计算公式为:
l=__________________.
探索新知
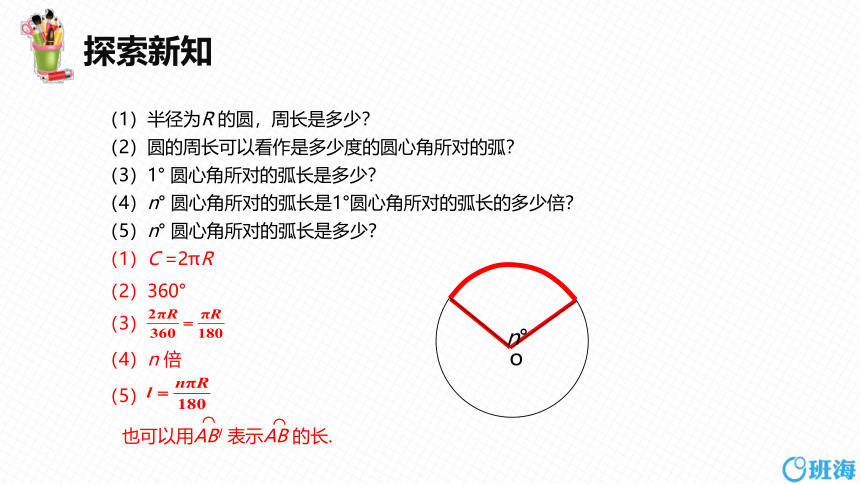
(1)半径为R 的圆,周长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
(3)1° 圆心角所对的弧长是多少?
(4)n° 圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
(5)n° 圆心角所对的弧长是多少?
(1)C =2πR
(2)360°
(3)
(4)n 倍
(5)
也可以用ABl 表示AB 的长.
n°
o
⌒
⌒
探索新知
1.弧、弧长、弧的度数间的关系:
弧相等表示弧长、弧的度数都相等;
度数相等的弧,弧长不一定相等;
弧长相等的弧,弧的度数不一定相等.
2.易错警示:在弧长公式 l= 中,n 表示1° 的n
倍,180表示1° 的180倍,n,180不带单位.
探索新知
制作弯形管道时,需要先按中心线计算 “展直长度”再下料.试计算如图所示的管道 的展直长度,即 的长(结果精确到0.1 mm).
例1
解:
R= 40mm,n = 110,所以
的长= 76.8 (mm).
因此,管道的展直长度约为76.8 mm.
探索新知
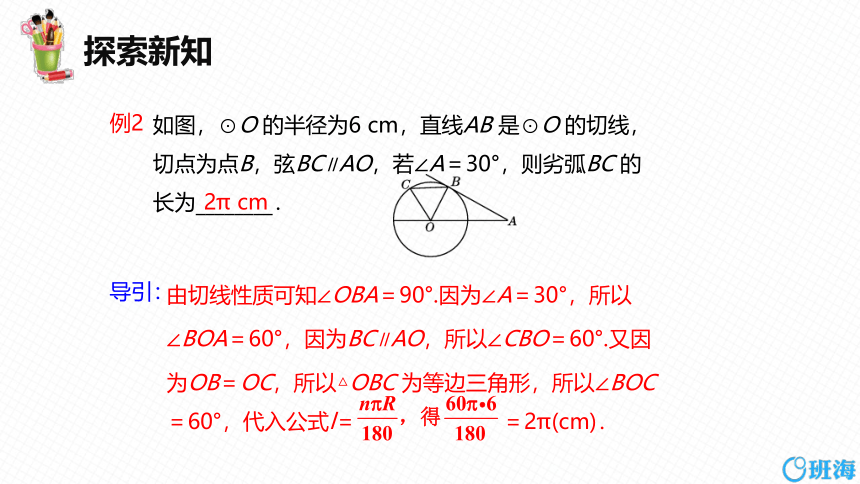
如图,⊙O 的半径为6 cm,直线AB 是⊙O 的切线,切点为点B,弦BC∥AO,若∠A=30°,则劣弧BC 的长为________.
例2
导引:
由切线性质可知∠OBA=90°.因为∠A=30°,所以
∠BOA=60°,因为BC∥AO,所以∠CBO=60°.又因
为OB=OC,所以△OBC 为等边三角形,所以∠BOC=60°,代入公式l= =2π(cm).
2π cm
探索新知
总 结
求弧长需要两个条件:
(1)弧所在圆的半径;
(2)弧所对的圆心角.
当题中没有直接给出这两个条件时,则需利用圆的相关知识:弦、弦心距、圆周角、切线等求出圆的半径或弧所对的圆心角.
典题精讲
如图,某田径场的周长(内圈)为400 m,其中两个弯道内圈(半圆形)共长200 m,直线段共长200 m,而每条跑道宽约1 m (共6条跑道).
(1) 内圈弯道半径为多少米?(结果精确到0.1 m)
一个内圈弯道与一个外圈弯道的长相差多少米?(结果精确到0.1 m)
1
典题精讲
解:
(1)设内圈弯道的半径为r m.由题意知 ×2πr=100.
解得r ≈31.8.∴内圈弯道的半径约为31.8 m.
(2)设外圈弯道的半径为R m.
∵共有6条跑道,故外圈弯道的半径R=
∴一个外圈弯道的弧长为
×2πR=πR=π =(100+6π)(m).
∴一个内圈弯道与一个外圈弯道的长相差约
100+6π-100=6π≈18.8(m).
典题精讲
在半径为6的⊙O 中,60°圆心角所对的弧长是( )
A.π B.2π
C.4π D.6π
2
B
如图,⊙O 是△ABC 的外接圆,BC=2,∠BAC=30°,则BC 的长等于( )
A. B.
C. D.
3
︵
A
典题精讲
如图,⊙O 的半径为3,四边形ABCD 内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则BD 的长为( )
A.π
B. π
C.2π
D.3π
4
︵
C
典题精讲
如图,在 ABCD 中,∠B=70°,BC=6,以AD 为直径的⊙O 交CD 于点E,则DE 的长为( )
A. π
B. π
C. π
D. π
5
︵
B
探索新知
2
知识点
扇形面积公式
在一块空旷的草地上有一根柱子,柱子上拴着 一条长
3 m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,
那么它的最大活动区域有多大?
探索新知
1.半径为R 的圆,面积是多少?
2.圆面可以看作是多少度的圆心角所对的扇形?
3.1°圆心角所对扇形面积是多少?
1. S=πR 2
2. 360°
3.
若设⊙O 半径为R, n°的圆
心角所对的扇形面积为S,则
A
B
O
思考1:
探索新知
思考2:扇形面积的大小与哪些因素有关系?
扇形面积的大小与扇形的半径和圆心角有关.
探索新知
比较扇形面积公式与弧长公式,可以用弧长表示扇形面积:
其中l 为扇形的弧长,R 为半径.
探索新知
扇形AOB 的半径为12 cm, ∠ AOB=120°,求
的长(结果精确到 0.1 cm)和扇形AOB 的面积(结果精
确到0.1 cm2).
例3
解:
的长= 25.1 ( cm).
S扇形= 150.7 (cm2 ).
因此, 的长约为25.1 cm,扇形AOB 的面积约为150.7 cm2.
探索新知
如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD 变形为以A 为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB 的面积为( )
A.6
B.7
C.8
D.9
例4
D
探索新知
导引:
由正方形的边长为3,可得弧BD 的弧长为6,然后利用
扇形的面积公式:S扇形DAB= lR,计算即可.
由条件可知:扇形的弧DCB 的长就是正方形的边BC 与
CD 长的和,为6,半径为3,则S扇形= ×6×3=9.
探索新知
总 结
扇形的面积计算有两个公式:
1.当已知扇形的圆心角时,用公式S扇形= 较为简便;
2.当知道扇形的弧长时,用公式S扇形= lR 较为简便.
探索新知
如图,在⊙O 中,弦BC 垂直于半径OA,垂足为点E,D 是优弧BC 上的一点,∠ADB=30°.
(1)求∠AOC 的度数;
(2)若弦BC=6,求图中阴影部分的面积.
例5
探索新知
导引:
(1)根据垂径定理得到相等的弧,再由同圆或等圆中,
弧、圆心角、圆周角之间的关系求得∠AOC 的度数;
(2)先求出⊙O 的半径,再求出圆心角∠BOC 的度数,
利用面积差求出阴影部分的面积.
探索新知
解:
(1)∵弦BC 垂直于半径OA,∴BE=CE, .
又∵∠ADB=30°,∴∠AOC=∠BOA=60°.
(2)∵BC=6,∴CE= BC=3.
在Rt△OCE 中,∠OCE=30°,
设OE=x,则OC=2x,CE= x=3,解得x= .
∴OE= ,OC=2 . ∵ ,
∴∠BOC=2∠AOC=120°,∴S阴影=S扇形OBC-S△OBC
= ×π×(2 )2- ×6× =4π-3 .
探索新知
总 结
本例中求弓形面积可转化为两个规则的基本图形(扇形、三角形)面积的差来解决.将所求面积转化为其他几个规则图形面积的和或差,是求阴影面积最常用的方法.
典题精讲
如图,水平放置的一个油管的横截面半径为12 cm,
其中有油的部分油面高 6cm,求截面上有油部分的
面积(结果精确到0.1 cm2).
1
.
0
A
B
典题精讲
解:
如图,连接OA,OB. 设OC⊥AB 于点C,交圆O 于点D.
∵CD=6 cm,OD=OA=12 cm,∴OC=12-6=6(cm).在Rt△AOC 中,
AC=
∴AB=12 cm,cos ∠COA=
∴∠COA=60°. ∴∠AOB=120°.
∴截面上有油部分的面积为S扇形AOB-S△AOB
= ≈88.4(cm2).
典题精讲
如图,半圆的直径BC 恰与等腰直角三角形ABC 的一条直角边完全重合,若BC=4,则图中阴影部分的面积是( )
A.2+π
B.2+2π
C.4+π
D.2+4π
2
A
典题精讲
如图,AB 是⊙O 的直径,BT 是⊙O 的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
A.2
B. π
C.1
D. π
3
C
典题精讲
如图,正方形ABCD 内接于半径为2的⊙O,则图中阴影部分的面积为( )
A.π+1
B.π+2
C.π-1
D.π-2
4
D
易错提醒
已知AB 所对的圆周角为30°,AB 所在圆的半径为30 cm,求AB 的长.
∵AB 所对的圆周角为30°,
∴AB 所对的圆心角为60°,
∴AB 的长l= =10π(cm).
︵
︵
︵
解:
︵
︵
︵
易错点:对弧长公式及扇形面积公式中的n 的意义理解不
充分而致错.
易错提醒
在公式l= ,S扇形= 中,n° 是圆心角的度数,而题干给出的是圆周角的度数,不能直接代入公式计算,要求出圆心角的度数后再代入公式计算.本题易错解为
AB 的长= =5π (cm).
易错总结:
︵
学以致用
小试牛刀
如图,在Rt△AOB 中,∠AOB=90°,OA=3,OB=2,将Rt△AOB 绕点O 顺时针旋转90°后得Rt△FOE,将线段EF 绕点E 逆时针旋转90°后得线段ED,分别以O,E 为圆心,OA,ED 长为半径画弧AF 和弧DF,连接AD,则图中阴影部分的面积是( )
A.π
B.
C.3+π
D.8-π
1
D
小试牛刀
如图,点O 是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使AB 和AC 都经过圆心O,则阴影部分的面积是⊙O 面积的( )
A.
B.
C.
D.
2
︵
︵
B
小试牛刀
方法1 用割补法求不规则图形的面积
3 如图,AB 为半圆O 的直径,AC 是⊙O 的一条弦,D 为BC的中点,作DE⊥AC,交AB 的延长线于点F,连接DA.
(1)求证:EF 为半圆O 的切线;
(2)若DA=DF=6 ,求阴影区域
的面积(结果保留根号和π).
小试牛刀
如图,连接OD,
∵D 为BC 的中点,
∴∠CAD=∠BAD.
∵OA=OD,∴∠BAD=∠ADO.
∴∠CAD=∠ADO.
∵DE⊥AC,∴∠E=90°.
∴∠CAD+∠EDA=90°,
即∠ADO+∠EDA=90°.
∴OD⊥EF.∴EF 为半圆O 的切线.
(1)证明:
小试牛刀
如图,连接OC 与CD,
∵DA=DF,
∴∠BAD=∠F.
∴∠BAD=∠F=∠CAD.
又∵∠BAD+∠CAD+∠F=90°,
∴∠F=30°,∠BAC=60°.
∵OC=OA,
∴△AOC 为等边三角形.
∴∠AOC=60°,∠COB=120°.
(2)解:
小试牛刀
∵OD⊥EF,∠F=30°,
∴∠DOF=60°.
在Rt△ODF 中,DF=6 ,
∴OD=DF tan 30°=6.
在Rt△AED 中,DA=6 ,∠CAD=30°,
∴DE=DA sin 30°=3 ,EA=DA cos 30°=9.
∵∠COD=180°-∠AOC-∠DOF=60°,
OC=OD,∴∠DCO=∠ODC=60°.
∴CD∥AB.
小试牛刀
故S△ACD=S△COD.
∴S阴影=S△AED-S扇形COD
小试牛刀
方法2 用变换法求不规则图形的面积
4 如图,在⊙O 中,半径OA⊥OB,过OA 的中点C 作FD∥OB 交⊙O于 D,F 两点,且CD= ,以O 为圆心,OC 为半径作CE,交OB 于E 点.
(1)求⊙O 的半径OA 的长;
(2)计算阴影部分的面积.
小试牛刀
(1)连接OD,∵OA⊥OB,FD∥OB,
∴∠OCD=90°.
设OC=a,则OA=2a=OD.
在△OCD 中,由勾股定理,
得CD 2+OC 2=OD 2,即( )2+a 2=4a 2,
解得a1=1,a2=-1(舍去).
∴半径OA 的长为2a=2.
解:
小试牛刀
(2)S△OCD= OC CD=
在Rt△OCD 中,∵OC=1,OD=2,
∴∠ODC=30°.
又∵FD∥OB,∴∠DOB=30°.
S阴影=S△OCD+S扇形OBD-S扇形OCE
小试牛刀
方法3 用整体思想求扇形的面积
5 如图,分别以五边形ABCDE 的顶点为圆心,1为半径作五个圆,则图中阴影部分的面积之和为( )
A. π B.3π
C. π D.2π
C
小试牛刀
方法4 用替换法求不规则图形的面积
6 如图,在边长为a 的正方形ABCD 中,以点A 为圆心、AB 为半径画弧得到扇形ABD,分别以AB,AD 为直径的两个半圆交于点E,求图中阴影部分的面积.
小试牛刀
如图,连接AE,并延长交弧BD 于点F,连接BE.
由轴对称的性质可知S扇形ABF=S扇形ADF,
S1=S2=S5,S3=S4.
∵∠BAE=∠DAE=45°,
∴S半圆形AB=
S扇形ABF=
∴S半圆形AB=S扇形ABF,
∴S1=S4=S2=S3=S5.
解:
小试牛刀
又∵S1+S5=S半圆形AB-S△ABE=
∴S阴影=S1+S2+S3+S4
=2(S1+S5)
课堂小结
课堂小结
通过本课时的学习,需要我们掌握:
1.弧长的计算公式l= 并运用公式进行计算.
2.扇形的面积公式S= 并运用公式进行计算.
3.弧长l 及扇形的面积S 之间的关系,
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
9 弧长及扇形的面积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们在小学学习了圆的面积和扇形的面积,也学习了圆的周长,那么圆上一部分的长,也就是一条弧的长怎么去求呢?现在重新学习圆的面积和扇形面积,比以前是不是有了更深的要求呢?
下面我们就来学习本节内容.
新课精讲
探索新知
1
知识点
弧长公式
如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品A
被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被
传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
探索新知
归 纳
在半径为R 的圆中, n° 的圆心角所对的弧长的计算公式为:
l=__________________.
探索新知
(1)半径为R 的圆,周长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
(3)1° 圆心角所对的弧长是多少?
(4)n° 圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
(5)n° 圆心角所对的弧长是多少?
(1)C =2πR
(2)360°
(3)
(4)n 倍
(5)
也可以用ABl 表示AB 的长.
n°
o
⌒
⌒
探索新知
1.弧、弧长、弧的度数间的关系:
弧相等表示弧长、弧的度数都相等;
度数相等的弧,弧长不一定相等;
弧长相等的弧,弧的度数不一定相等.
2.易错警示:在弧长公式 l= 中,n 表示1° 的n
倍,180表示1° 的180倍,n,180不带单位.
探索新知
制作弯形管道时,需要先按中心线计算 “展直长度”再下料.试计算如图所示的管道 的展直长度,即 的长(结果精确到0.1 mm).
例1
解:
R= 40mm,n = 110,所以
的长= 76.8 (mm).
因此,管道的展直长度约为76.8 mm.
探索新知
如图,⊙O 的半径为6 cm,直线AB 是⊙O 的切线,切点为点B,弦BC∥AO,若∠A=30°,则劣弧BC 的长为________.
例2
导引:
由切线性质可知∠OBA=90°.因为∠A=30°,所以
∠BOA=60°,因为BC∥AO,所以∠CBO=60°.又因
为OB=OC,所以△OBC 为等边三角形,所以∠BOC=60°,代入公式l= =2π(cm).
2π cm
探索新知
总 结
求弧长需要两个条件:
(1)弧所在圆的半径;
(2)弧所对的圆心角.
当题中没有直接给出这两个条件时,则需利用圆的相关知识:弦、弦心距、圆周角、切线等求出圆的半径或弧所对的圆心角.
典题精讲
如图,某田径场的周长(内圈)为400 m,其中两个弯道内圈(半圆形)共长200 m,直线段共长200 m,而每条跑道宽约1 m (共6条跑道).
(1) 内圈弯道半径为多少米?(结果精确到0.1 m)
一个内圈弯道与一个外圈弯道的长相差多少米?(结果精确到0.1 m)
1
典题精讲
解:
(1)设内圈弯道的半径为r m.由题意知 ×2πr=100.
解得r ≈31.8.∴内圈弯道的半径约为31.8 m.
(2)设外圈弯道的半径为R m.
∵共有6条跑道,故外圈弯道的半径R=
∴一个外圈弯道的弧长为
×2πR=πR=π =(100+6π)(m).
∴一个内圈弯道与一个外圈弯道的长相差约
100+6π-100=6π≈18.8(m).
典题精讲
在半径为6的⊙O 中,60°圆心角所对的弧长是( )
A.π B.2π
C.4π D.6π
2
B
如图,⊙O 是△ABC 的外接圆,BC=2,∠BAC=30°,则BC 的长等于( )
A. B.
C. D.
3
︵
A
典题精讲
如图,⊙O 的半径为3,四边形ABCD 内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则BD 的长为( )
A.π
B. π
C.2π
D.3π
4
︵
C
典题精讲
如图,在 ABCD 中,∠B=70°,BC=6,以AD 为直径的⊙O 交CD 于点E,则DE 的长为( )
A. π
B. π
C. π
D. π
5
︵
B
探索新知
2
知识点
扇形面积公式
在一块空旷的草地上有一根柱子,柱子上拴着 一条长
3 m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,
那么它的最大活动区域有多大?
探索新知
1.半径为R 的圆,面积是多少?
2.圆面可以看作是多少度的圆心角所对的扇形?
3.1°圆心角所对扇形面积是多少?
1. S=πR 2
2. 360°
3.
若设⊙O 半径为R, n°的圆
心角所对的扇形面积为S,则
A
B
O
思考1:
探索新知
思考2:扇形面积的大小与哪些因素有关系?
扇形面积的大小与扇形的半径和圆心角有关.
探索新知
比较扇形面积公式与弧长公式,可以用弧长表示扇形面积:
其中l 为扇形的弧长,R 为半径.
探索新知
扇形AOB 的半径为12 cm, ∠ AOB=120°,求
的长(结果精确到 0.1 cm)和扇形AOB 的面积(结果精
确到0.1 cm2).
例3
解:
的长= 25.1 ( cm).
S扇形= 150.7 (cm2 ).
因此, 的长约为25.1 cm,扇形AOB 的面积约为150.7 cm2.
探索新知
如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD 变形为以A 为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB 的面积为( )
A.6
B.7
C.8
D.9
例4
D
探索新知
导引:
由正方形的边长为3,可得弧BD 的弧长为6,然后利用
扇形的面积公式:S扇形DAB= lR,计算即可.
由条件可知:扇形的弧DCB 的长就是正方形的边BC 与
CD 长的和,为6,半径为3,则S扇形= ×6×3=9.
探索新知
总 结
扇形的面积计算有两个公式:
1.当已知扇形的圆心角时,用公式S扇形= 较为简便;
2.当知道扇形的弧长时,用公式S扇形= lR 较为简便.
探索新知
如图,在⊙O 中,弦BC 垂直于半径OA,垂足为点E,D 是优弧BC 上的一点,∠ADB=30°.
(1)求∠AOC 的度数;
(2)若弦BC=6,求图中阴影部分的面积.
例5
探索新知
导引:
(1)根据垂径定理得到相等的弧,再由同圆或等圆中,
弧、圆心角、圆周角之间的关系求得∠AOC 的度数;
(2)先求出⊙O 的半径,再求出圆心角∠BOC 的度数,
利用面积差求出阴影部分的面积.
探索新知
解:
(1)∵弦BC 垂直于半径OA,∴BE=CE, .
又∵∠ADB=30°,∴∠AOC=∠BOA=60°.
(2)∵BC=6,∴CE= BC=3.
在Rt△OCE 中,∠OCE=30°,
设OE=x,则OC=2x,CE= x=3,解得x= .
∴OE= ,OC=2 . ∵ ,
∴∠BOC=2∠AOC=120°,∴S阴影=S扇形OBC-S△OBC
= ×π×(2 )2- ×6× =4π-3 .
探索新知
总 结
本例中求弓形面积可转化为两个规则的基本图形(扇形、三角形)面积的差来解决.将所求面积转化为其他几个规则图形面积的和或差,是求阴影面积最常用的方法.
典题精讲
如图,水平放置的一个油管的横截面半径为12 cm,
其中有油的部分油面高 6cm,求截面上有油部分的
面积(结果精确到0.1 cm2).
1
.
0
A
B
典题精讲
解:
如图,连接OA,OB. 设OC⊥AB 于点C,交圆O 于点D.
∵CD=6 cm,OD=OA=12 cm,∴OC=12-6=6(cm).在Rt△AOC 中,
AC=
∴AB=12 cm,cos ∠COA=
∴∠COA=60°. ∴∠AOB=120°.
∴截面上有油部分的面积为S扇形AOB-S△AOB
= ≈88.4(cm2).
典题精讲
如图,半圆的直径BC 恰与等腰直角三角形ABC 的一条直角边完全重合,若BC=4,则图中阴影部分的面积是( )
A.2+π
B.2+2π
C.4+π
D.2+4π
2
A
典题精讲
如图,AB 是⊙O 的直径,BT 是⊙O 的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
A.2
B. π
C.1
D. π
3
C
典题精讲
如图,正方形ABCD 内接于半径为2的⊙O,则图中阴影部分的面积为( )
A.π+1
B.π+2
C.π-1
D.π-2
4
D
易错提醒
已知AB 所对的圆周角为30°,AB 所在圆的半径为30 cm,求AB 的长.
∵AB 所对的圆周角为30°,
∴AB 所对的圆心角为60°,
∴AB 的长l= =10π(cm).
︵
︵
︵
解:
︵
︵
︵
易错点:对弧长公式及扇形面积公式中的n 的意义理解不
充分而致错.
易错提醒
在公式l= ,S扇形= 中,n° 是圆心角的度数,而题干给出的是圆周角的度数,不能直接代入公式计算,要求出圆心角的度数后再代入公式计算.本题易错解为
AB 的长= =5π (cm).
易错总结:
︵
学以致用
小试牛刀
如图,在Rt△AOB 中,∠AOB=90°,OA=3,OB=2,将Rt△AOB 绕点O 顺时针旋转90°后得Rt△FOE,将线段EF 绕点E 逆时针旋转90°后得线段ED,分别以O,E 为圆心,OA,ED 长为半径画弧AF 和弧DF,连接AD,则图中阴影部分的面积是( )
A.π
B.
C.3+π
D.8-π
1
D
小试牛刀
如图,点O 是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使AB 和AC 都经过圆心O,则阴影部分的面积是⊙O 面积的( )
A.
B.
C.
D.
2
︵
︵
B
小试牛刀
方法1 用割补法求不规则图形的面积
3 如图,AB 为半圆O 的直径,AC 是⊙O 的一条弦,D 为BC的中点,作DE⊥AC,交AB 的延长线于点F,连接DA.
(1)求证:EF 为半圆O 的切线;
(2)若DA=DF=6 ,求阴影区域
的面积(结果保留根号和π).
小试牛刀
如图,连接OD,
∵D 为BC 的中点,
∴∠CAD=∠BAD.
∵OA=OD,∴∠BAD=∠ADO.
∴∠CAD=∠ADO.
∵DE⊥AC,∴∠E=90°.
∴∠CAD+∠EDA=90°,
即∠ADO+∠EDA=90°.
∴OD⊥EF.∴EF 为半圆O 的切线.
(1)证明:
小试牛刀
如图,连接OC 与CD,
∵DA=DF,
∴∠BAD=∠F.
∴∠BAD=∠F=∠CAD.
又∵∠BAD+∠CAD+∠F=90°,
∴∠F=30°,∠BAC=60°.
∵OC=OA,
∴△AOC 为等边三角形.
∴∠AOC=60°,∠COB=120°.
(2)解:
小试牛刀
∵OD⊥EF,∠F=30°,
∴∠DOF=60°.
在Rt△ODF 中,DF=6 ,
∴OD=DF tan 30°=6.
在Rt△AED 中,DA=6 ,∠CAD=30°,
∴DE=DA sin 30°=3 ,EA=DA cos 30°=9.
∵∠COD=180°-∠AOC-∠DOF=60°,
OC=OD,∴∠DCO=∠ODC=60°.
∴CD∥AB.
小试牛刀
故S△ACD=S△COD.
∴S阴影=S△AED-S扇形COD
小试牛刀
方法2 用变换法求不规则图形的面积
4 如图,在⊙O 中,半径OA⊥OB,过OA 的中点C 作FD∥OB 交⊙O于 D,F 两点,且CD= ,以O 为圆心,OC 为半径作CE,交OB 于E 点.
(1)求⊙O 的半径OA 的长;
(2)计算阴影部分的面积.
小试牛刀
(1)连接OD,∵OA⊥OB,FD∥OB,
∴∠OCD=90°.
设OC=a,则OA=2a=OD.
在△OCD 中,由勾股定理,
得CD 2+OC 2=OD 2,即( )2+a 2=4a 2,
解得a1=1,a2=-1(舍去).
∴半径OA 的长为2a=2.
解:
小试牛刀
(2)S△OCD= OC CD=
在Rt△OCD 中,∵OC=1,OD=2,
∴∠ODC=30°.
又∵FD∥OB,∴∠DOB=30°.
S阴影=S△OCD+S扇形OBD-S扇形OCE
小试牛刀
方法3 用整体思想求扇形的面积
5 如图,分别以五边形ABCDE 的顶点为圆心,1为半径作五个圆,则图中阴影部分的面积之和为( )
A. π B.3π
C. π D.2π
C
小试牛刀
方法4 用替换法求不规则图形的面积
6 如图,在边长为a 的正方形ABCD 中,以点A 为圆心、AB 为半径画弧得到扇形ABD,分别以AB,AD 为直径的两个半圆交于点E,求图中阴影部分的面积.
小试牛刀
如图,连接AE,并延长交弧BD 于点F,连接BE.
由轴对称的性质可知S扇形ABF=S扇形ADF,
S1=S2=S5,S3=S4.
∵∠BAE=∠DAE=45°,
∴S半圆形AB=
S扇形ABF=
∴S半圆形AB=S扇形ABF,
∴S1=S4=S2=S3=S5.
解:
小试牛刀
又∵S1+S5=S半圆形AB-S△ABE=
∴S阴影=S1+S2+S3+S4
=2(S1+S5)
课堂小结
课堂小结
通过本课时的学习,需要我们掌握:
1.弧长的计算公式l= 并运用公式进行计算.
2.扇形的面积公式S= 并运用公式进行计算.
3.弧长l 及扇形的面积S 之间的关系,
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
