【班海精品】北师大版(新)九年级下-1.1锐角三角函数 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-1.1锐角三角函数 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览





文档简介
(共43张PPT)
1 锐角三角函数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
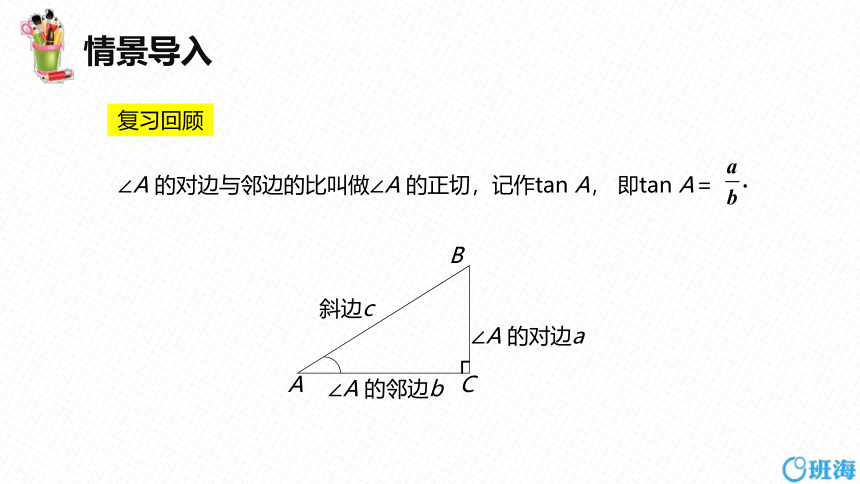
复习回顾
∠A 的对边与邻边的比叫做∠A 的正切,记作tan A, 即tan A=
A
B
C
∠A 的对边a
┌
斜边c
∠A 的邻边b
新课精讲
探索新知
1
知识点
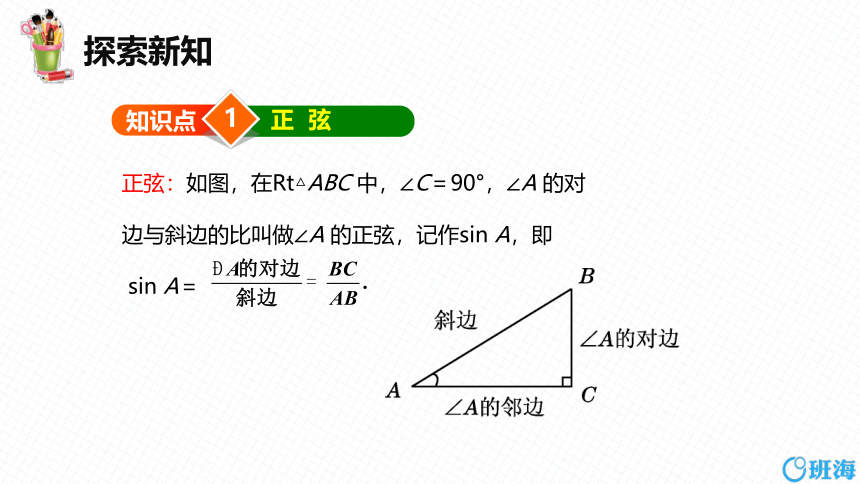
正 弦
正弦:如图,在Rt△ABC 中,∠C=90°,∠A 的对
边与斜边的比叫做∠A 的正弦,记作sin A,即
sin A=
探索新知
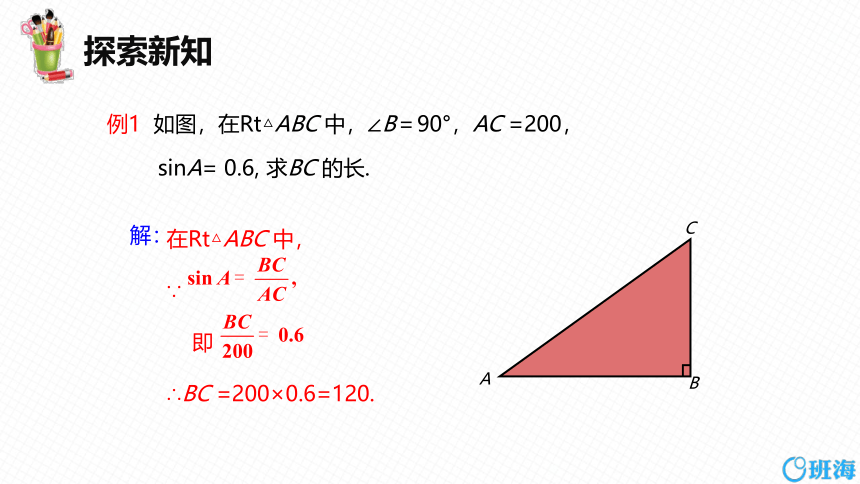
例1 如图,在Rt△ABC 中,∠B=90°,AC =200,
sinA= 0.6, 求BC 的长.
在Rt△ABC 中,
∵
即
∴BC =200×0.6=120.
解:
A
B
C
┌
典题精讲
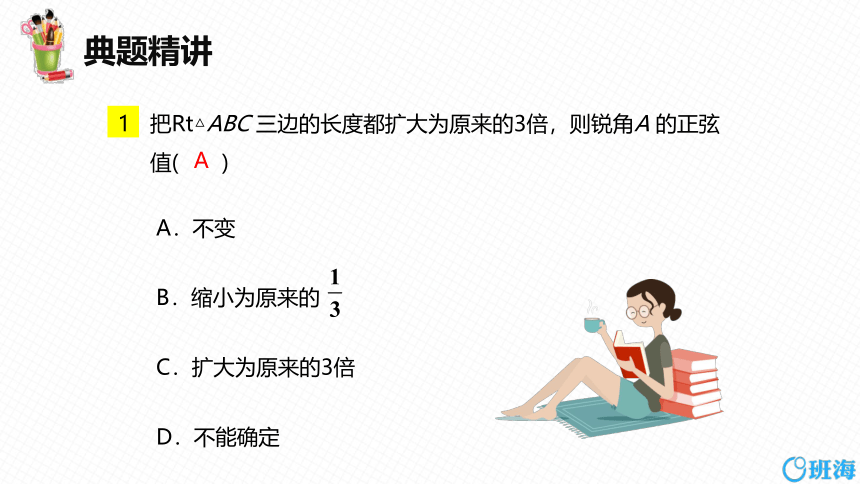
把Rt△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
A
典题精讲
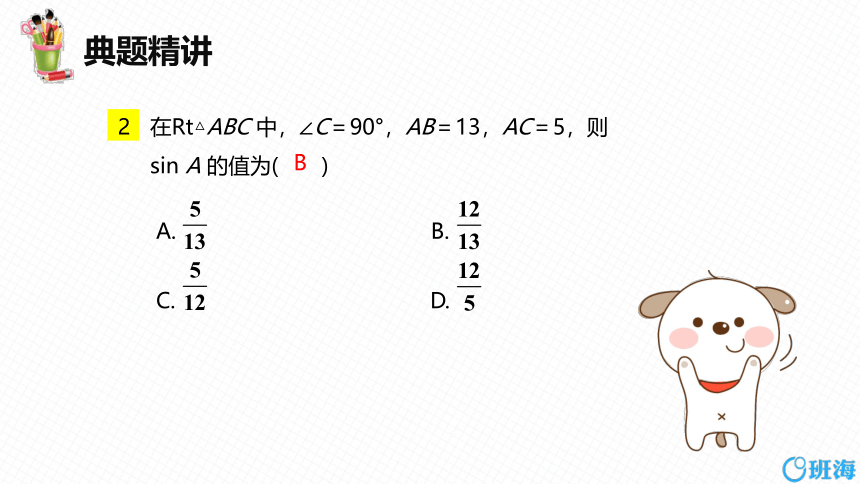
在Rt△ABC 中,∠C=90°,AB=13,AC=5,则sin A 的值为( )
A. B.
C. D.
B
典题精讲
如图,在平面直角坐标系中,点A 的坐标为(3,4),那么sin α 的值是( )
A.
B.
C.
D.
C
探索新知
2
知识点
余弦
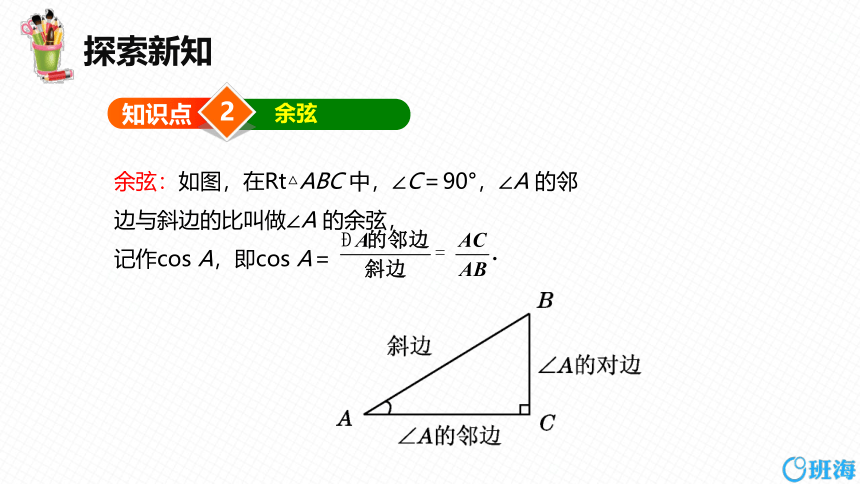
余弦:如图,在Rt△ABC 中,∠C=90°,∠A 的邻
边与斜边的比叫做∠A 的余弦,
记作cos A,即cos A=
解:∵∠C=90°,AC=12,BC=5,
∴AB=
∴sin A= cos A=
探索新知
例2 如图,在Rt△ABC 中,
∠C= 90°,AC=12,
BC=5,求sin A,cos A的值.
导引:在Rt△ABC 中,已知两直角边长,可先用勾股定理求
斜边长,再利用定义分别求出sin A,cos A 的值.
探索新知
总 结
在直角三角形中,求锐角的正弦和余弦时,一定要根据正弦和余弦的定义求解.其中未知边的长度往往借助勾股定理进行求解.
探索新知
例3 如图,在Rt△ABC 中,∠C=90°,sin A= BC=40,
求△ABC 的周长和面积.
已知BC=40,求△ABC 的周长,
则还需要求出其他两边的长,借
助sin A 的值可求出AB 的长,再
利用勾股定理求出AC 的长即可,
直角三角形的面积等于两直角边
长乘积的一半.
导引:
探索新知
解:∵sin A= ∴AB=
∵BC=40,sin A= ,∴AB=50.
又∵AC=
∴△ABC 的周长为AB+AC+BC=120,
△ABC 的面积为 BC·AC= ×40×30=600.
探索新知
总 结
正弦的定义表达式sin A= 可根据解题需要变形为
BC=AB sin A 或AB=
余弦的定义表达式cos A= 也可变形为
AC=AB cos A 或AB= .
典题精讲
如图,已知在Rt△ABC 中,∠C= 90°,AB=5,BC=3,则cos B 的值是( )
A.
B.
C.
D.
A
典题精讲
如图,在Rt△ABC 中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.
B.
C.
D.
A
典题精讲
已知在Rt△ABC 中,∠C=90°,如果BC=2,
∠A=α,则AC 的长为( )
A.2sin α
B.2cos α
C.2tan α
D.
D
典题精讲
如图,在平面直角坐标系中,点A 的坐标为(4,3),那么
cos α 的值是( )
A. B.
C. D.
D
探索新知
3
知识点
锐角三角函数的取值范围
锐角三角函数的取值范围:
在Rt△ABC 中,因为各边边长都是正数,且斜边边长
大于直角边边长,所以对于锐角A,有tan A>0,
0<sin A<1,0<cos A<1.
探索新知
例4 如图,在Rt△ABC 中,∠C=90°,AC=4,BC=3,
求∠A,∠B 的三角函数值.
由已知AC 与BC 的长可确定∠A 与∠B 的正切,但要
确定∠A 与∠B 的正弦与余弦,根据定义必须确定
斜边AB 的长,这就需要先用勾股定理计算AB 的长.
导引:
探索新知
在Rt△ABC 中,∠C=90°,AC=4,BC=3,
∴AB=5.
∴sin A= cos A=
tan A= sin B=
cos B= tan B=
解:
探索新知
总 结
求一个直角三角形中锐角的三角函数值时,
①若已知两边长,先根据勾股定理求第三边长,然后根
据概念直接求;
②若已知两边的比,则设辅助未知数表示出两边长,然
后再用方法①求.
典题精讲
若α 是锐角,sin α=3m-2,则m 的取值范围是( )
A. <m<1 B.2<m<3
C.0<m<1 D.m>
如果0°<∠A<90°,并且cos A 是方程
(x-0.35)=0的一个根,那么cos A=_______.
A
0.35
易错提醒
已知x=cos α (α 为锐角)满足方程2x 2-5x+2=0,求cos α 的值.
易错点:忽视锐角的余弦值的取值范围.
方程2x 2-5x+2=0的解是x1=2,x2=
∵0<cos α<1,∴cos α=
常见错解:方程2x 2-5x+2=0的解是x1=2,x2=
此时忽略了cos α (α 为锐角)的取值范围是0<cos α<1,而错得cos α=2或cos α=
解:
学以致用
小试牛刀
如图,在Rt△ABC 中,∠BAC=90°, AD⊥BC 于点D,
则下列结论不正确的是( )
A.sin B=
B.sin B=
C.sin B=
D.sin B=
C
小试牛刀
2 在Rt△ABC 中,∠C=90°,若AB=4,sin A= ,
则斜边上的高等于( )
A. B.
C. D.
B
小试牛刀
3 如图,在矩形ABCD 中,E 是BC 边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:△ABE ≌ △DFA;
(2)如果AD=10,AB=6,求sin ∠EDF 的值.
小试牛刀
(1) 在矩形ABCD 中,BC=AD,AD∥BC,∠B=90°,
∴∠AEB=∠DAF.
∵DF⊥AE,AE=BC,
∴∠AFD=90°=∠B,AE=AD.
∴△ABE ≌ △DFA (AAS).
证明:
小试牛刀
(2)由(1)知△ABE ≌ △DFA,∴AB=DF=6.
在Rt△ADF 中,AF=
∴EF=AE-AF=AD-AF=2.
在Rt△DFE 中,DE=
∴sin ∠EDF=
解:
小试牛刀
4 如图,在△ABC 中,∠ACB=90°,sin A= ,BC=8,D 是AB 的中点,过点B 作直线CD 的垂线,垂足为点E.求:
(1)线段CD 的长;
(2)cos∠ABE 的值.
小试牛刀
(1)在△ABC 中,∵∠ACB=90°,BC=8,
sin A= ∴AB=10.
∵D 是AB 的中点,∴CD= AB=5.
(2)在Rt△ABC 中,∵AB=10,BC=8,
∴AC= ∵D 是AB 的中点,
∴BD=5,S△BDC=S△ADC. ∴S△BDC= S△ABC,
即 CD BE= × AC BC.∴BE=
在Rt△BDE 中,cos∠DBE=
即cos∠ABE=
解:
小试牛刀
5 在△ABC 中,∠A,∠B,∠C 的对边分别是a,b,c,其中a,b 是关于x 的一元二次方程x 2-(c+4)x+4c+8=0的两个根,且9c=25a sin A.
(1)试判断△ABC 的形状;
(2)求△ABC 的三边长.
小试牛刀
(1)∵a,b 是关于x 的一元二次方程x 2-(c+4)x+4c+8=0的两个根,
∴a+b=c+4,ab=4c+8.
∴a 2+b 2=(a+b)2-2ab=(c+4)2-2(4c+8),
即a 2+b 2=c 2.
∴△ABC 为直角三角形.
∵(a-b)2=(a+b)2-4ab=(c+4)2-4(4c+8)=c 2-8c- 16,不能确定(a-b)2的值是否为0,
∴不能确定a=b,即△ABC 为直角三角形.
解:
小试牛刀
(2)∵△ABC 是直角三角形,
∴sin A=
将其代入9c=25a sin A,得9c=25a
∴9c 2=25a 2. ∴3c=5a.
∴c=
∴b=
将b= c= 代入a+b=c+4,解得a=6.
∴b= ×6=8,c= ×6=10,
即△ABC 的三边长分别为6,8,10.
小试牛刀
6 如图,E 是矩形ABCD 中CD 边上一点,△BCE 沿BE 折叠得△BFE,点F 落在边AD 上.
(1)求证:△ABF∽△DFE;
(2)若sin∠DFE= ,求tan∠EBC 的值.
小试牛刀
(1) 由题意可得∠A=∠D=∠C=∠BFE=90°,
∴∠ABF=90°-∠AFB,∠DFE=180°-∠BFE-∠AFB=90°-∠AFB.
∴∠ABF=∠DFE.
∴△ABF∽△DFE.
证明:
小试牛刀
(2)由折叠可得FB=BC,EF=EC.
∵sin∠DFE=13,
即EF=3DE. ∴AB=CD=DE+EC=DE+EF=4DE,DF=
∵△ABF∽△DFE,∴
即FB=
又∵FB=BC,EF=EC,
∴tan ∠EBC=
解:
课堂小结
课堂小结
锐角三角函数定义:
A
B
C
∠A 的对边a
┌
斜边c
∠A 的邻边b
锐角三角函数的取值范围:
对于锐角A,有tan A>0,0<sin A<1,0<cos A<1.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1 锐角三角函数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
∠A 的对边与邻边的比叫做∠A 的正切,记作tan A, 即tan A=
A
B
C
∠A 的对边a
┌
斜边c
∠A 的邻边b
新课精讲
探索新知
1
知识点
正 弦
正弦:如图,在Rt△ABC 中,∠C=90°,∠A 的对
边与斜边的比叫做∠A 的正弦,记作sin A,即
sin A=
探索新知
例1 如图,在Rt△ABC 中,∠B=90°,AC =200,
sinA= 0.6, 求BC 的长.
在Rt△ABC 中,
∵
即
∴BC =200×0.6=120.
解:
A
B
C
┌
典题精讲
把Rt△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
A
典题精讲
在Rt△ABC 中,∠C=90°,AB=13,AC=5,则sin A 的值为( )
A. B.
C. D.
B
典题精讲
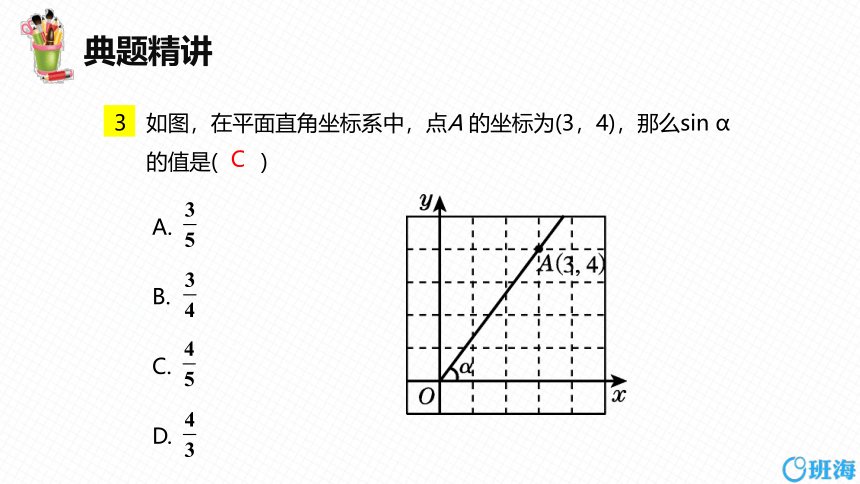
如图,在平面直角坐标系中,点A 的坐标为(3,4),那么sin α 的值是( )
A.
B.
C.
D.
C
探索新知
2
知识点
余弦
余弦:如图,在Rt△ABC 中,∠C=90°,∠A 的邻
边与斜边的比叫做∠A 的余弦,
记作cos A,即cos A=
解:∵∠C=90°,AC=12,BC=5,
∴AB=
∴sin A= cos A=
探索新知
例2 如图,在Rt△ABC 中,
∠C= 90°,AC=12,
BC=5,求sin A,cos A的值.
导引:在Rt△ABC 中,已知两直角边长,可先用勾股定理求
斜边长,再利用定义分别求出sin A,cos A 的值.
探索新知
总 结
在直角三角形中,求锐角的正弦和余弦时,一定要根据正弦和余弦的定义求解.其中未知边的长度往往借助勾股定理进行求解.
探索新知
例3 如图,在Rt△ABC 中,∠C=90°,sin A= BC=40,
求△ABC 的周长和面积.
已知BC=40,求△ABC 的周长,
则还需要求出其他两边的长,借
助sin A 的值可求出AB 的长,再
利用勾股定理求出AC 的长即可,
直角三角形的面积等于两直角边
长乘积的一半.
导引:
探索新知
解:∵sin A= ∴AB=
∵BC=40,sin A= ,∴AB=50.
又∵AC=
∴△ABC 的周长为AB+AC+BC=120,
△ABC 的面积为 BC·AC= ×40×30=600.
探索新知
总 结
正弦的定义表达式sin A= 可根据解题需要变形为
BC=AB sin A 或AB=
余弦的定义表达式cos A= 也可变形为
AC=AB cos A 或AB= .
典题精讲
如图,已知在Rt△ABC 中,∠C= 90°,AB=5,BC=3,则cos B 的值是( )
A.
B.
C.
D.
A
典题精讲
如图,在Rt△ABC 中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.
B.
C.
D.
A
典题精讲
已知在Rt△ABC 中,∠C=90°,如果BC=2,
∠A=α,则AC 的长为( )
A.2sin α
B.2cos α
C.2tan α
D.
D
典题精讲
如图,在平面直角坐标系中,点A 的坐标为(4,3),那么
cos α 的值是( )
A. B.
C. D.
D
探索新知
3
知识点
锐角三角函数的取值范围
锐角三角函数的取值范围:
在Rt△ABC 中,因为各边边长都是正数,且斜边边长
大于直角边边长,所以对于锐角A,有tan A>0,
0<sin A<1,0<cos A<1.
探索新知
例4 如图,在Rt△ABC 中,∠C=90°,AC=4,BC=3,
求∠A,∠B 的三角函数值.
由已知AC 与BC 的长可确定∠A 与∠B 的正切,但要
确定∠A 与∠B 的正弦与余弦,根据定义必须确定
斜边AB 的长,这就需要先用勾股定理计算AB 的长.
导引:
探索新知
在Rt△ABC 中,∠C=90°,AC=4,BC=3,
∴AB=5.
∴sin A= cos A=
tan A= sin B=
cos B= tan B=
解:
探索新知
总 结
求一个直角三角形中锐角的三角函数值时,
①若已知两边长,先根据勾股定理求第三边长,然后根
据概念直接求;
②若已知两边的比,则设辅助未知数表示出两边长,然
后再用方法①求.
典题精讲
若α 是锐角,sin α=3m-2,则m 的取值范围是( )
A. <m<1 B.2<m<3
C.0<m<1 D.m>
如果0°<∠A<90°,并且cos A 是方程
(x-0.35)=0的一个根,那么cos A=_______.
A
0.35
易错提醒
已知x=cos α (α 为锐角)满足方程2x 2-5x+2=0,求cos α 的值.
易错点:忽视锐角的余弦值的取值范围.
方程2x 2-5x+2=0的解是x1=2,x2=
∵0<cos α<1,∴cos α=
常见错解:方程2x 2-5x+2=0的解是x1=2,x2=
此时忽略了cos α (α 为锐角)的取值范围是0<cos α<1,而错得cos α=2或cos α=
解:
学以致用
小试牛刀
如图,在Rt△ABC 中,∠BAC=90°, AD⊥BC 于点D,
则下列结论不正确的是( )
A.sin B=
B.sin B=
C.sin B=
D.sin B=
C
小试牛刀
2 在Rt△ABC 中,∠C=90°,若AB=4,sin A= ,
则斜边上的高等于( )
A. B.
C. D.
B
小试牛刀
3 如图,在矩形ABCD 中,E 是BC 边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:△ABE ≌ △DFA;
(2)如果AD=10,AB=6,求sin ∠EDF 的值.
小试牛刀
(1) 在矩形ABCD 中,BC=AD,AD∥BC,∠B=90°,
∴∠AEB=∠DAF.
∵DF⊥AE,AE=BC,
∴∠AFD=90°=∠B,AE=AD.
∴△ABE ≌ △DFA (AAS).
证明:
小试牛刀
(2)由(1)知△ABE ≌ △DFA,∴AB=DF=6.
在Rt△ADF 中,AF=
∴EF=AE-AF=AD-AF=2.
在Rt△DFE 中,DE=
∴sin ∠EDF=
解:
小试牛刀
4 如图,在△ABC 中,∠ACB=90°,sin A= ,BC=8,D 是AB 的中点,过点B 作直线CD 的垂线,垂足为点E.求:
(1)线段CD 的长;
(2)cos∠ABE 的值.
小试牛刀
(1)在△ABC 中,∵∠ACB=90°,BC=8,
sin A= ∴AB=10.
∵D 是AB 的中点,∴CD= AB=5.
(2)在Rt△ABC 中,∵AB=10,BC=8,
∴AC= ∵D 是AB 的中点,
∴BD=5,S△BDC=S△ADC. ∴S△BDC= S△ABC,
即 CD BE= × AC BC.∴BE=
在Rt△BDE 中,cos∠DBE=
即cos∠ABE=
解:
小试牛刀
5 在△ABC 中,∠A,∠B,∠C 的对边分别是a,b,c,其中a,b 是关于x 的一元二次方程x 2-(c+4)x+4c+8=0的两个根,且9c=25a sin A.
(1)试判断△ABC 的形状;
(2)求△ABC 的三边长.
小试牛刀
(1)∵a,b 是关于x 的一元二次方程x 2-(c+4)x+4c+8=0的两个根,
∴a+b=c+4,ab=4c+8.
∴a 2+b 2=(a+b)2-2ab=(c+4)2-2(4c+8),
即a 2+b 2=c 2.
∴△ABC 为直角三角形.
∵(a-b)2=(a+b)2-4ab=(c+4)2-4(4c+8)=c 2-8c- 16,不能确定(a-b)2的值是否为0,
∴不能确定a=b,即△ABC 为直角三角形.
解:
小试牛刀
(2)∵△ABC 是直角三角形,
∴sin A=
将其代入9c=25a sin A,得9c=25a
∴9c 2=25a 2. ∴3c=5a.
∴c=
∴b=
将b= c= 代入a+b=c+4,解得a=6.
∴b= ×6=8,c= ×6=10,
即△ABC 的三边长分别为6,8,10.
小试牛刀
6 如图,E 是矩形ABCD 中CD 边上一点,△BCE 沿BE 折叠得△BFE,点F 落在边AD 上.
(1)求证:△ABF∽△DFE;
(2)若sin∠DFE= ,求tan∠EBC 的值.
小试牛刀
(1) 由题意可得∠A=∠D=∠C=∠BFE=90°,
∴∠ABF=90°-∠AFB,∠DFE=180°-∠BFE-∠AFB=90°-∠AFB.
∴∠ABF=∠DFE.
∴△ABF∽△DFE.
证明:
小试牛刀
(2)由折叠可得FB=BC,EF=EC.
∵sin∠DFE=13,
即EF=3DE. ∴AB=CD=DE+EC=DE+EF=4DE,DF=
∵△ABF∽△DFE,∴
即FB=
又∵FB=BC,EF=EC,
∴tan ∠EBC=
解:
课堂小结
课堂小结
锐角三角函数定义:
A
B
C
∠A 的对边a
┌
斜边c
∠A 的邻边b
锐角三角函数的取值范围:
对于锐角A,有tan A>0,0<sin A<1,0<cos A<1.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
