【班海精品】北师大版(新)九年级下-1.1锐角三角函数 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)九年级下-1.1锐角三角函数 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 08:56:33 | ||
图片预览








文档简介
(共45张PPT)
1 锐角三角函数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
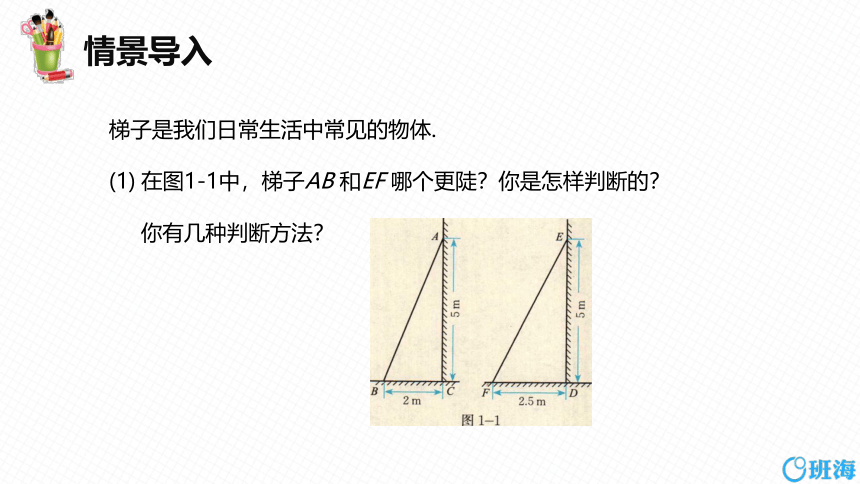
梯子是我们日常生活中常见的物体.
在图1-1中,梯子AB 和EF 哪个更陡?你是怎样判断的?
你有几种判断方法?
情景导入
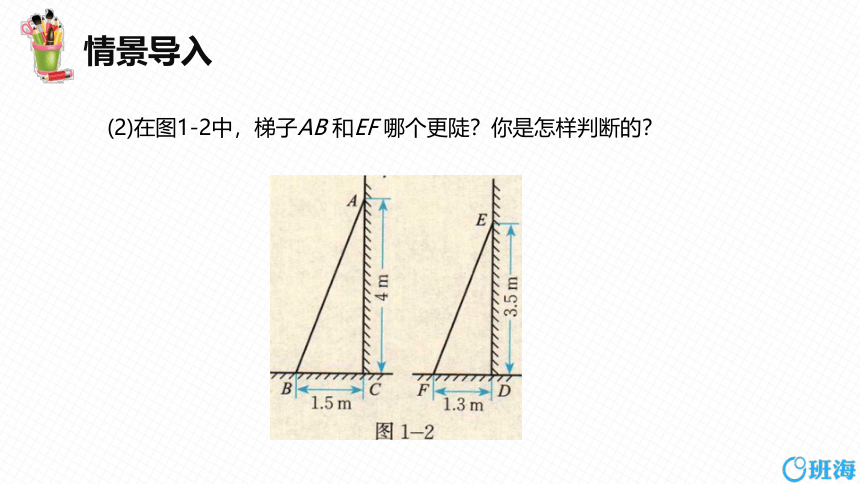
(2)在图1-2中,梯子AB 和EF 哪个更陡?你是怎样判断的?
新课精讲
探索新知
1
知识点
正切的定义
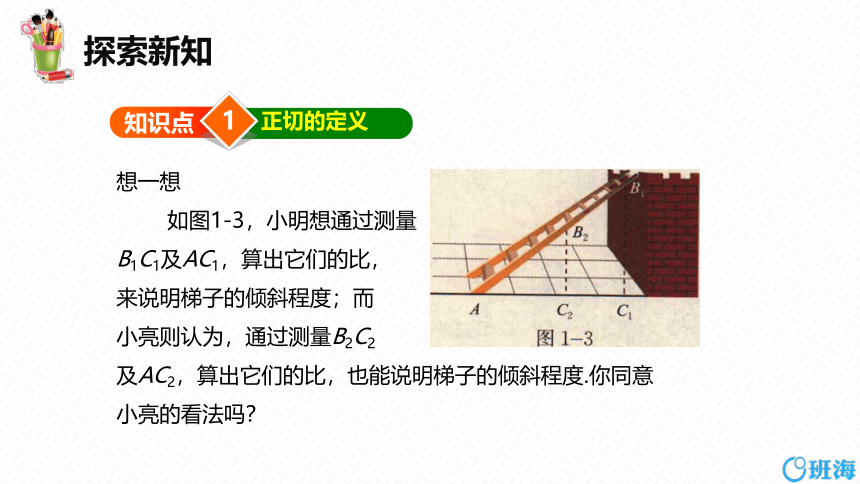
想一想
如图1-3,小明想通过测量
B1C1及AC1,算出它们的比,
来说明梯子的倾斜程度;而
小亮则认为,通过测量B2C2
及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?
探索新知
(1)直角三角形AB1C1和直角三角形AB2C2有什么关系?
有什么关系
如果改变B2在梯子上的位置呢?由此你能得出什么结论
探索新知
归 纳
改变点B 的位置, 的值始终不变。
探索新知
如图,在Rt△ABC 中,∠C=90°
我们把锐角A 的邻边与对边的比叫做∠A 的正切,
记作tanA,即
A
B
C
∠A的对边
┌
斜边
∠A的邻边
探索新知
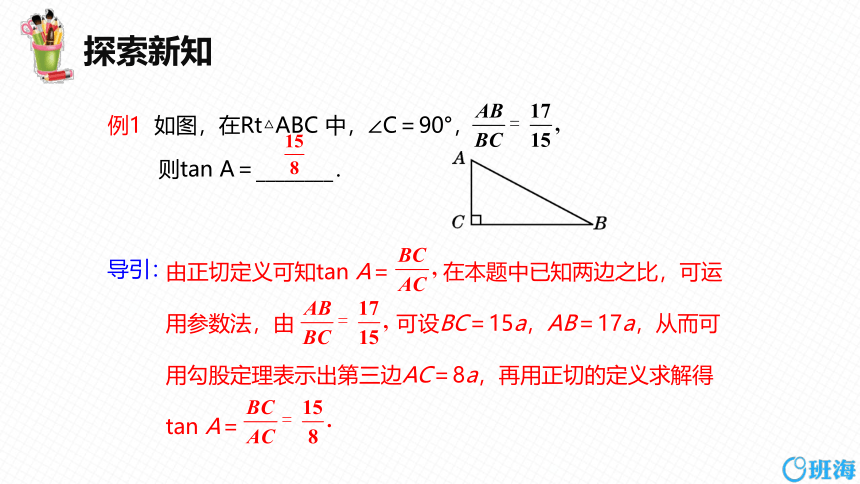
例1 如图,在Rt△ABC 中,∠C=90°,
则tan A=________.
由正切定义可知tan A= 在本题中已知两边之比,可运
用参数法,由 可设BC=15a,AB=17a,从而可
用勾股定理表示出第三边AC=8a,再用正切的定义求解得
tan A=
导引:
探索新知
总 结
直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利
用勾股定理求出未知的直角边,再利用正切的定义求解.
探索新知
例2 如图,在Rt△ABC 中,∠ACB=90°,AC=8,BC=6,
CD⊥AB,垂足为D,则tan∠BCD=________.
根据题意得∠BCD=∠CAB,
所以tan ∠BCD=tan ∠CAB=
导引:
探索新知
总 结
直接求某个锐角的正切值有困难时,可以考虑利用中间量进行转化,可以是相等的角作为中间量,还可以利用相似,得到相等的比作为中间量.
典题精讲
在Rt△ABC 中,∠C=90°,AB=5,BC=3,则tan A 的值是( )
A. B.
C. D.
1
A
在Rt△ABC 中,∠C=90°,若斜边AB 是直角边BC 的3倍,则tan B的值是( )
A. B. 3
C. D.
2
D
典题精讲
如图,在△ABC 中,∠C=90°,BC∶AC=1∶3,则tan B 的值是( )
3
C.
D.
3
A
典题精讲
一个直角三角形中,如果各边的长度都扩大为原来的2倍,
那么它的两个锐角的正切值( )
A.都没有变化
B.都扩大为原来的2倍
C.都缩小为原来的一半
D.不能确定是否发生变化
A
探索新知
2
知识点
正切的应用
议一议
在图1 -3中,梯子的倾斜程度与tanA 有关系吗
探索新知
总 结
tanA 的值越大,梯子越陡.
1. 当梯子与地面所成的角为锐角A 时,
tan A= tan A 的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2. 当倾斜角确定时,其对边与邻边之比随之确定,这一比
值只与倾斜角的大小有关,而与物体的长度无关.
解:甲梯中,
乙梯中,
因为tanα>tanβ,所以甲梯更陡.
探索新知
例3 如图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
探索新知
总 结
(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程度,因为夹角的正切值越大,则夹角越大,物体放置得越“陡”.
典题精讲
解: ∵△ABC 是等腰三角形,
BD⊥AC,
∴D 是AC 的中点.
∴DC=AD= AC=2.
在Rt△BCD 中,tan C= = = .
如图, △ABC 是等腰三角形,你能根据图中所给数据求出tanC吗?
1
B
C
典题精讲
2 如图,在网格中,小正方形的边长均为1,点A,B,C 都在格点上,则∠ABC 的正切值是( )
A.2
B.
C.
D.
D
典题精讲
在Rt△ABC 中,CD 为斜边AB 上的高,且CD=2,
BD=8,则tan A 的值是( )
A.2 B.4
C. D.
B
探索新知
3
知识点
坡度(坡角)与正切的关系
探究
一、如图是某一大坝的横断面:
坡面AB 的垂直高度与水平宽度AE 的长度之比是α 的什么三角函数?
α
A
C
B
D
E
坡面AB 与水平面的夹角叫做坡角.
探索新知
坡度的定义:
坡面的垂直高度与水平宽度之比
叫做坡度,记作 i .
α
A
B
E
h
l
坡度的概念,一要记住是一个比值而不是角度, 二要明确坡度其实就是坡角的正切.
探索新知
例4 以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
错解分析:概念不清,误以为坡度是一个角度,而猜测
坡度即为倾斜角的度数.
B
典题精讲
解:由勾股定理可知,
AC= = ≈192.289(m),
∴tan ∠BAC= ≈ ≈0.286.
所以,山的坡度大约是0.286.
如图,某人从山脚下的点A 走了 200 m 后到达山顶的点B,已知点B到山脚的垂直距离为55 m,求山的坡度(结果精确到0.001).
1
B
典题精讲
如图,梯子(长度不变)跟地面所成的锐角为∠A. 关于∠A 的正切值与梯子的倾斜程度的关系,下列叙述正确的是( )
A.tan A 的值越大,梯子越缓
B.tan A 的值越小,梯子越陡
C.tan A 的值越大,梯子越陡
D.梯子的陡缓程度与∠A 的正切值无关
2
C
典题精讲
3 如图,铁路路基横断面为一个四边形,其中AD∥BC.
若两斜坡的坡度均为i=2∶3,顶宽是3 m,路基高是
4 m,则路基的下底宽是( )
A.7 m B.9 m C.12 m D.15 m
D
易错提醒
在等腰三角形ABC 中,AB=AC=10,BC=12,则tan B=________.
易错点:忽略求正切值的前提.
学以致用
小试牛刀
如图,BD 是菱形ABCD 的对角线,CE⊥AB 于点E,交BD 于
点F,且点E 是边AB 的中点,则tan∠BFE 的值是( )
A.
B.2
C.
D.
D
小试牛刀
如图,点A (t,3)在第一象限,OA 与x 轴所夹的锐角为α,
tan α= ,则t 的值是( )
A.1
B.1.5
C.2
D.3
C
小试牛刀
在△ABC 中,∠A,∠B,∠C 所对的边分别为a,b,c,a,b,c
满足(2b) 2=4(c-a)(c+a),且5a-3c=0,求tan A+tan B 的值.
∵(2b)2=4(c-a)(c+a),
∴a 2+b 2=c 2. ∴∠C=90°.
又∵5a-3c=0,∴5a=3c.
设a=3k,则c=5k. ∴b=4k.
∴tan A+tan B=
解:
小试牛刀
如图,CD 是一个平面镜,光线从点A 射入经CD 上的点E 反射
后照射到点B. 设入射角为α (入射角等于反射角),AC⊥CD,
BD⊥CD,垂足分别为C,D. 若AC=3,BD=6,CD=12.求
tan α 的值.
小试牛刀
∵AC⊥CD,BD⊥CD,
∴∠ACE=∠BDE=90°.
又∵入射角等于反射角,
∴∠A=∠B=α.
∴△ACE∽△BDE.
∴
∵AC=3,BD=6,CD=12,∴CE=4.
∴tan α=tan A=
解:
小试牛刀
5 如图,在△ABC 中,∠C=150°,AC=4,tan B=
(1)求BC 的长;
(2)利用此图形求tan 15°的值(结果精确到0.1,参考数据: ≈1.4, ≈1.7, ≈2.2).
小试牛刀
(1)过点A 作AD⊥BC,交BC 的延长线于点D,如图所示.
在Rt△ADC 中,AC=4,∵∠ACB=150°,
∴∠ACD=30°.
∴AD= AC=2,CD=
在Rt△ABD 中,tan B=
∴BD=16. ∴BC=BD-CD=16-
解:
小试牛刀
(2)在BC 边上取一点M,使得CM=AC,连接AM,如图所示.
∵∠ACB=150°,∴∠AMC=∠MAC=15°,tan 15°=tan ∠AMD=
小试牛刀
某宾馆在重新装修,准备在大厅的主楼梯上铺设某种红地毯.如果主楼梯的坡度为1∶ ,且楼梯的竖直高度为3 m,
如图所示.
(1)至少需要多长的地毯?(结果保留一位小数)
(2)若所铺设的地毯每平方米售价30元,主楼梯的宽度为2 m,你作为经理给采购人员至少多少元钱去购买地毯?
小试牛刀
(1)∵主楼梯的坡度为1∶ ,
∴
∵BC=3 m,
∴AB= m.
∴AB+BC=3+ ≈ 8.2(m).
答:至少需要8.2 m的地毯.
(2)8.2×2×30=492(元).
答:给采购人员至少492元钱去购买地毯.
解:
课堂小结
课堂小结
正切:∠A 的对边与邻边的比叫做∠A 的正切,
记作tan A, 即tan A=
A
B
C
∠A 的对边a
┌
斜边c
∠A 的邻边b
坡度(坡角)与正切的关系:
坡度就是坡角的正切.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1 锐角三角函数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
梯子是我们日常生活中常见的物体.
在图1-1中,梯子AB 和EF 哪个更陡?你是怎样判断的?
你有几种判断方法?
情景导入
(2)在图1-2中,梯子AB 和EF 哪个更陡?你是怎样判断的?
新课精讲
探索新知
1
知识点
正切的定义
想一想
如图1-3,小明想通过测量
B1C1及AC1,算出它们的比,
来说明梯子的倾斜程度;而
小亮则认为,通过测量B2C2
及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?
探索新知
(1)直角三角形AB1C1和直角三角形AB2C2有什么关系?
有什么关系
如果改变B2在梯子上的位置呢?由此你能得出什么结论
探索新知
归 纳
改变点B 的位置, 的值始终不变。
探索新知
如图,在Rt△ABC 中,∠C=90°
我们把锐角A 的邻边与对边的比叫做∠A 的正切,
记作tanA,即
A
B
C
∠A的对边
┌
斜边
∠A的邻边
探索新知
例1 如图,在Rt△ABC 中,∠C=90°,
则tan A=________.
由正切定义可知tan A= 在本题中已知两边之比,可运
用参数法,由 可设BC=15a,AB=17a,从而可
用勾股定理表示出第三边AC=8a,再用正切的定义求解得
tan A=
导引:
探索新知
总 结
直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利
用勾股定理求出未知的直角边,再利用正切的定义求解.
探索新知
例2 如图,在Rt△ABC 中,∠ACB=90°,AC=8,BC=6,
CD⊥AB,垂足为D,则tan∠BCD=________.
根据题意得∠BCD=∠CAB,
所以tan ∠BCD=tan ∠CAB=
导引:
探索新知
总 结
直接求某个锐角的正切值有困难时,可以考虑利用中间量进行转化,可以是相等的角作为中间量,还可以利用相似,得到相等的比作为中间量.
典题精讲
在Rt△ABC 中,∠C=90°,AB=5,BC=3,则tan A 的值是( )
A. B.
C. D.
1
A
在Rt△ABC 中,∠C=90°,若斜边AB 是直角边BC 的3倍,则tan B的值是( )
A. B. 3
C. D.
2
D
典题精讲
如图,在△ABC 中,∠C=90°,BC∶AC=1∶3,则tan B 的值是( )
3
C.
D.
3
A
典题精讲
一个直角三角形中,如果各边的长度都扩大为原来的2倍,
那么它的两个锐角的正切值( )
A.都没有变化
B.都扩大为原来的2倍
C.都缩小为原来的一半
D.不能确定是否发生变化
A
探索新知
2
知识点
正切的应用
议一议
在图1 -3中,梯子的倾斜程度与tanA 有关系吗
探索新知
总 结
tanA 的值越大,梯子越陡.
1. 当梯子与地面所成的角为锐角A 时,
tan A= tan A 的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2. 当倾斜角确定时,其对边与邻边之比随之确定,这一比
值只与倾斜角的大小有关,而与物体的长度无关.
解:甲梯中,
乙梯中,
因为tanα>tanβ,所以甲梯更陡.
探索新知
例3 如图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
探索新知
总 结
(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程度,因为夹角的正切值越大,则夹角越大,物体放置得越“陡”.
典题精讲
解: ∵△ABC 是等腰三角形,
BD⊥AC,
∴D 是AC 的中点.
∴DC=AD= AC=2.
在Rt△BCD 中,tan C= = = .
如图, △ABC 是等腰三角形,你能根据图中所给数据求出tanC吗?
1
B
C
典题精讲
2 如图,在网格中,小正方形的边长均为1,点A,B,C 都在格点上,则∠ABC 的正切值是( )
A.2
B.
C.
D.
D
典题精讲
在Rt△ABC 中,CD 为斜边AB 上的高,且CD=2,
BD=8,则tan A 的值是( )
A.2 B.4
C. D.
B
探索新知
3
知识点
坡度(坡角)与正切的关系
探究
一、如图是某一大坝的横断面:
坡面AB 的垂直高度与水平宽度AE 的长度之比是α 的什么三角函数?
α
A
C
B
D
E
坡面AB 与水平面的夹角叫做坡角.
探索新知
坡度的定义:
坡面的垂直高度与水平宽度之比
叫做坡度,记作 i .
α
A
B
E
h
l
坡度的概念,一要记住是一个比值而不是角度, 二要明确坡度其实就是坡角的正切.
探索新知
例4 以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
错解分析:概念不清,误以为坡度是一个角度,而猜测
坡度即为倾斜角的度数.
B
典题精讲
解:由勾股定理可知,
AC= = ≈192.289(m),
∴tan ∠BAC= ≈ ≈0.286.
所以,山的坡度大约是0.286.
如图,某人从山脚下的点A 走了 200 m 后到达山顶的点B,已知点B到山脚的垂直距离为55 m,求山的坡度(结果精确到0.001).
1
B
典题精讲
如图,梯子(长度不变)跟地面所成的锐角为∠A. 关于∠A 的正切值与梯子的倾斜程度的关系,下列叙述正确的是( )
A.tan A 的值越大,梯子越缓
B.tan A 的值越小,梯子越陡
C.tan A 的值越大,梯子越陡
D.梯子的陡缓程度与∠A 的正切值无关
2
C
典题精讲
3 如图,铁路路基横断面为一个四边形,其中AD∥BC.
若两斜坡的坡度均为i=2∶3,顶宽是3 m,路基高是
4 m,则路基的下底宽是( )
A.7 m B.9 m C.12 m D.15 m
D
易错提醒
在等腰三角形ABC 中,AB=AC=10,BC=12,则tan B=________.
易错点:忽略求正切值的前提.
学以致用
小试牛刀
如图,BD 是菱形ABCD 的对角线,CE⊥AB 于点E,交BD 于
点F,且点E 是边AB 的中点,则tan∠BFE 的值是( )
A.
B.2
C.
D.
D
小试牛刀
如图,点A (t,3)在第一象限,OA 与x 轴所夹的锐角为α,
tan α= ,则t 的值是( )
A.1
B.1.5
C.2
D.3
C
小试牛刀
在△ABC 中,∠A,∠B,∠C 所对的边分别为a,b,c,a,b,c
满足(2b) 2=4(c-a)(c+a),且5a-3c=0,求tan A+tan B 的值.
∵(2b)2=4(c-a)(c+a),
∴a 2+b 2=c 2. ∴∠C=90°.
又∵5a-3c=0,∴5a=3c.
设a=3k,则c=5k. ∴b=4k.
∴tan A+tan B=
解:
小试牛刀
如图,CD 是一个平面镜,光线从点A 射入经CD 上的点E 反射
后照射到点B. 设入射角为α (入射角等于反射角),AC⊥CD,
BD⊥CD,垂足分别为C,D. 若AC=3,BD=6,CD=12.求
tan α 的值.
小试牛刀
∵AC⊥CD,BD⊥CD,
∴∠ACE=∠BDE=90°.
又∵入射角等于反射角,
∴∠A=∠B=α.
∴△ACE∽△BDE.
∴
∵AC=3,BD=6,CD=12,∴CE=4.
∴tan α=tan A=
解:
小试牛刀
5 如图,在△ABC 中,∠C=150°,AC=4,tan B=
(1)求BC 的长;
(2)利用此图形求tan 15°的值(结果精确到0.1,参考数据: ≈1.4, ≈1.7, ≈2.2).
小试牛刀
(1)过点A 作AD⊥BC,交BC 的延长线于点D,如图所示.
在Rt△ADC 中,AC=4,∵∠ACB=150°,
∴∠ACD=30°.
∴AD= AC=2,CD=
在Rt△ABD 中,tan B=
∴BD=16. ∴BC=BD-CD=16-
解:
小试牛刀
(2)在BC 边上取一点M,使得CM=AC,连接AM,如图所示.
∵∠ACB=150°,∴∠AMC=∠MAC=15°,tan 15°=tan ∠AMD=
小试牛刀
某宾馆在重新装修,准备在大厅的主楼梯上铺设某种红地毯.如果主楼梯的坡度为1∶ ,且楼梯的竖直高度为3 m,
如图所示.
(1)至少需要多长的地毯?(结果保留一位小数)
(2)若所铺设的地毯每平方米售价30元,主楼梯的宽度为2 m,你作为经理给采购人员至少多少元钱去购买地毯?
小试牛刀
(1)∵主楼梯的坡度为1∶ ,
∴
∵BC=3 m,
∴AB= m.
∴AB+BC=3+ ≈ 8.2(m).
答:至少需要8.2 m的地毯.
(2)8.2×2×30=492(元).
答:给采购人员至少492元钱去购买地毯.
解:
课堂小结
课堂小结
正切:∠A 的对边与邻边的比叫做∠A 的正切,
记作tan A, 即tan A=
A
B
C
∠A 的对边a
┌
斜边c
∠A 的邻边b
坡度(坡角)与正切的关系:
坡度就是坡角的正切.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
