【班海精品】冀教版(新)九下-29.5 正多边形与圆 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-29.5 正多边形与圆 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
29.5 正多边形与圆
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.观察下面的三幅图片,说说图片中各包含哪些多边形.
2.日常生活中我们经常看到哪些多边形形状的物体
新课精讲
探索新知
1
知识点
圆内接正多边形及相关定义
顶点都在同一圆上的正多边形叫做圆内接正多边形.
这个圆叫做该正多边形的外接圆.
正n 边形的各角相等,且每个内角为:
每个外角为:
探索新知
下列说法不正确的是( )
A.等边三角形是正多边形
B.各边相等,各角也相等的多边形是正多边形
C.菱形不一定是正多边形
D.各角相等的多边形是正多边形
例1
导引:
等边三角形是正三角形;各边相等,各角也相等的多边形是正多边形;当菱形的四个角相等时才是正多边形(正方形),所以菱形不一定是正多边形;D说法不正确. 答案:D
D
探索新知
总 结
正多边形的识别要从两个角度去看,
一是边都相等;
二是内角都相等.
探索新知
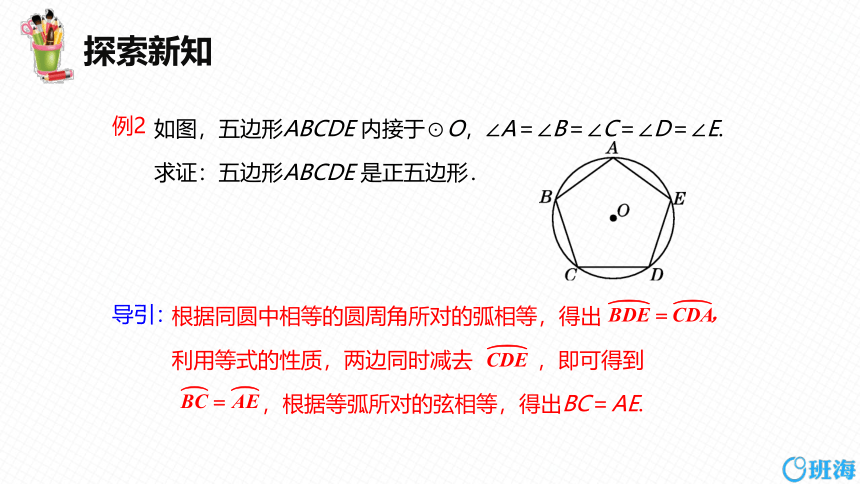
如图,五边形ABCDE 内接于⊙O,∠A=∠B=∠C=∠D=∠E.
求证:五边形ABCDE 是正五边形.
例2
导引:
根据同圆中相等的圆周角所对的弧相等,得出
利用等式的性质,两边同时减去 ,即可得到
,根据等弧所对的弦相等,得出BC=AE.
探索新知
解:
∵∠A=∠B=∠C=∠D=∠E,圆周角∠A对 ,
圆周角∠B 对 ,
∴ .
∴ ,即 .
∴BC=AE. 同理可证其余各边都相等.
∴五边形ABCDE 是正五边形.
探索新知
总 结
(1)证正多边形和圆的关系,在图形中找到圆的弧、弦等,利用同(等)弧所对的圆周角相等、所对的弦相等解答.其证明思路如下:角相等 弧相等 弦相等 正多边形.
(2)证明一个多边形是正多边形的方法:①利用定义,证出各边相等,各角相等;②利用圆内接多边形,证明各边所对的弧相等,即把圆n 等分,依次连接各等分点,所得多边形即为正多边形.
典题精讲
对于三角形,如果三边相等,那么它的三个角一定相等. 反过来, 如果三个角相等,那么它的三边也一定相等. 对于其他多边形,如果去掉 “各边相等”和“各角相等”两个条件中的任意一个,还能保证这个多边形是正多边形吗?请举例说明.
1
解:
不能.例如:菱形的各边都相等,但不是正多边形.
典题精讲
一个正多边形的边心距与边长的比为 ,求这个正多边形的边数.
2
解:
连接OA,OB,如图.
设OC=a,则AB=2a.
∴AC=BC=a.
∴∠AOC=∠BOC=45°,
∴∠AOB=90°.
∵360°÷90°=4.
∴这个正多边形的边数为4.
典题精讲
下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
正多边形的一边所对的中心角与该多边形的一个内角的关系为( )
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
3
4
A
B
典题精讲
若正方形的外接圆半径为2,则其内切圆半径为( )
A. B.
C. D.1
5
A
一个圆的内接正四边形和外切正四边形的面积的比是( )
A.1∶ B.1∶2
C.2∶3 D.2∶π
6
B
典题精讲
正六边形ABCDEF 内接于⊙O,正六边形的周长是12,则⊙O 的半径是( )
A.
B .2
C.
D.
7
B
探索新知
2
知识点
圆内接正多边形的画法
利用尺规作一个已知圆的内接正六边形.
由于正六边形的中心角为60°,因此它的边长就是其外接圆的半径R. 所以,在半径为R 的圆上,依次截取等于R 的弦,就可以六等分圆,进而作出 圆内接正六边形.
探索新知
用尺规作圆的内接正方形.
已知:如图,⊙O.
求作:正方形ABCD 内接于⊙O.
例3
探索新知
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD 都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD 为⊙O 的内接正方形.
探索新知
总 结
解决这类问题通常有两种方法:
(1)用量角器等分圆周法;
(2)用尺规等分圆周法.
典题精讲
如图,AD 为⊙O 的直径,作⊙O 的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D 为圆心,OD长为半径画圆弧,交⊙O 于B,C 两点;
(2)连接AB,BC,AC. △ABC 即为所求作的三角形.
乙:(1)作OD 的中垂线,交⊙O 于B,C 两点;
(2)连接AB,AC.△ABC 即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
1
C
典题精讲
在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).
2
解:
如图所示.
(答案不唯一)
易错提醒
一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
A.2 B. C.1 D.
A
易错点:误认为正多边形的边心距是正多边形的半径.
易错提醒
错解:B
诊断:设正多边形的边数为n. 因为正多边形的内角和为(n-2)·180°,正多边形的外角和为360°,根据题意得(n-2)·180°=360°×2,解得n=6,故正多边形为正六边形.边长为2的正六边形可以分成六个边长为2的正三角形,所以正多边形的半径等于2.产生错误的原因是认为正多边形的边心距是正多边形的半径,计算得出错误的结果 ,最后导致错选B.
学以致用
小试牛刀
如图,正六边形ABCDEF 内接于⊙O,若直线PA 与⊙O 相切于点A,则∠PAB 等于( )
A.30°
B.45°
C.150°
D.30°或150°
1
A
小试牛刀
以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
2
D
小试牛刀
如图,⊙O 是正五边形ABCDE 的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R 2-r 2=a 2
B.a=2R sin 36°
C.a=2r tan 36°
D.r=R cos 36°
3
A
小试牛刀
4 如图,点G,H 分别是正六边形ABCDEF 的边BC,CD上的
点,且BG=CH,AG 交BH 于点P.
(1)求证:△ABG ≌ △BCH;
(2)求∠APH 的度数.
(1)证明:∵六边形ABCDEF 为正六边形,∴AB=BC,∠ABC
=∠C=120°.在△ABG 与△BCH 中,
∴△ABG ≌ △BCH.
(2)解:由(1)知△ABG ≌ △BCH,∴∠BAG=∠HBC. ∴∠APH
=∠ABP+∠BAG=∠ABP+∠HBC=∠ABC=120°.
小试牛刀
5 作图与证明:
如图,已知⊙O 和⊙O上的一点A,请完成下列任务:
(1)作⊙O 的内接正六边形ABCDEF;
(2)连接BF,CE,判断四边形BCEF 的形
状并加以证明.
解:(1)如图①,首先作直径AD,然后分别
以A,D 为圆心,OA长为半径画弧,分
别交⊙O 于点B,F,C,E,连接AB,
BC,CD,DE,EF,AF,则正六边形
ABCDEF 即为所求作的图形.
小试牛刀
(2)四边形BCEF 是矩形.
证明:如图②,连接OE. ∵六边形ABCDEF 是正六边形,
∴AB=AF=DE=DC=FE=BC.
∴BF=CE.
∴四边形BCEF 是平行四边形.
∵∠EOD= =60°,OE=OD,
∴△EDO 是等边三角形.∴∠ODE=60°.
∴∠EDC=∠FED=2∠ODE=120°.
∵DE=DC,∴∠DEC=∠DCE=30°.
∴∠CEF=∠DEF-∠DEC=90°.
∴四边形BCEF 是矩形.
小试牛刀
如图,在⊙O 的内接四边形ABCD 中,AB=AD,∠C=120°,
点E 在 上.
(1)求∠AED 的度数;
(2)连接OD,OE,当∠DOE=90°时,AE 恰
好是⊙O 的内接正n 边形的一边,求n 的值.
解:(1)如图,连接BD.∵四边形ABCD 是⊙O 的内接四边形,
∴∠BAD+∠C=180°.∵∠C=120°,∴∠BAD=60°.
∵AB=AD,∴△ABD 是等边三角形.∴∠ABD=60°.
∵四边形ABDE 是⊙O 的内接四边形,
∴∠AED+∠ABD=180°.∴∠AED=120°.
(2)如图,连接OA. ∵∠ABD=60°,∴∠AOD=2∠ABD =120°.
又∵∠DOE=90°,∴∠AOE=∠AOD-∠DOE=30°,
∴n= =12.
小试牛刀
7 如图①、②、③、④分别是⊙O 的内接正三角形、正四边
形、正五边形、正n 边形,点M,N 分别从点B,C 开始以
相同的速度在⊙O 上逆时针运动,AM 与BN 相交于点P.
(1)图①中,∠APN=______;
(2)图②中,∠APN=______,图③中,∠APN=______;
(3)试探索∠APN 的度数与正多边形边数n 的关系(直接写答案).
解:(3)∠APN=
60°
90°
108°
课堂小结
课堂小结
正多边形:各边相等、各角也相等的多边形叫做
正多边形.
把一个圆n (n≥3)等分,顺次连接各等分点,就得
到一个正n 边形. 我们把这个正n 边形叫做圆的内
接正n 边形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.5 正多边形与圆
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.观察下面的三幅图片,说说图片中各包含哪些多边形.
2.日常生活中我们经常看到哪些多边形形状的物体
新课精讲
探索新知
1
知识点
圆内接正多边形及相关定义
顶点都在同一圆上的正多边形叫做圆内接正多边形.
这个圆叫做该正多边形的外接圆.
正n 边形的各角相等,且每个内角为:
每个外角为:
探索新知
下列说法不正确的是( )
A.等边三角形是正多边形
B.各边相等,各角也相等的多边形是正多边形
C.菱形不一定是正多边形
D.各角相等的多边形是正多边形
例1
导引:
等边三角形是正三角形;各边相等,各角也相等的多边形是正多边形;当菱形的四个角相等时才是正多边形(正方形),所以菱形不一定是正多边形;D说法不正确. 答案:D
D
探索新知
总 结
正多边形的识别要从两个角度去看,
一是边都相等;
二是内角都相等.
探索新知
如图,五边形ABCDE 内接于⊙O,∠A=∠B=∠C=∠D=∠E.
求证:五边形ABCDE 是正五边形.
例2
导引:
根据同圆中相等的圆周角所对的弧相等,得出
利用等式的性质,两边同时减去 ,即可得到
,根据等弧所对的弦相等,得出BC=AE.
探索新知
解:
∵∠A=∠B=∠C=∠D=∠E,圆周角∠A对 ,
圆周角∠B 对 ,
∴ .
∴ ,即 .
∴BC=AE. 同理可证其余各边都相等.
∴五边形ABCDE 是正五边形.
探索新知
总 结
(1)证正多边形和圆的关系,在图形中找到圆的弧、弦等,利用同(等)弧所对的圆周角相等、所对的弦相等解答.其证明思路如下:角相等 弧相等 弦相等 正多边形.
(2)证明一个多边形是正多边形的方法:①利用定义,证出各边相等,各角相等;②利用圆内接多边形,证明各边所对的弧相等,即把圆n 等分,依次连接各等分点,所得多边形即为正多边形.
典题精讲
对于三角形,如果三边相等,那么它的三个角一定相等. 反过来, 如果三个角相等,那么它的三边也一定相等. 对于其他多边形,如果去掉 “各边相等”和“各角相等”两个条件中的任意一个,还能保证这个多边形是正多边形吗?请举例说明.
1
解:
不能.例如:菱形的各边都相等,但不是正多边形.
典题精讲
一个正多边形的边心距与边长的比为 ,求这个正多边形的边数.
2
解:
连接OA,OB,如图.
设OC=a,则AB=2a.
∴AC=BC=a.
∴∠AOC=∠BOC=45°,
∴∠AOB=90°.
∵360°÷90°=4.
∴这个正多边形的边数为4.
典题精讲
下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
正多边形的一边所对的中心角与该多边形的一个内角的关系为( )
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
3
4
A
B
典题精讲
若正方形的外接圆半径为2,则其内切圆半径为( )
A. B.
C. D.1
5
A
一个圆的内接正四边形和外切正四边形的面积的比是( )
A.1∶ B.1∶2
C.2∶3 D.2∶π
6
B
典题精讲
正六边形ABCDEF 内接于⊙O,正六边形的周长是12,则⊙O 的半径是( )
A.
B .2
C.
D.
7
B
探索新知
2
知识点
圆内接正多边形的画法
利用尺规作一个已知圆的内接正六边形.
由于正六边形的中心角为60°,因此它的边长就是其外接圆的半径R. 所以,在半径为R 的圆上,依次截取等于R 的弦,就可以六等分圆,进而作出 圆内接正六边形.
探索新知
用尺规作圆的内接正方形.
已知:如图,⊙O.
求作:正方形ABCD 内接于⊙O.
例3
探索新知
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD 都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD 为⊙O 的内接正方形.
探索新知
总 结
解决这类问题通常有两种方法:
(1)用量角器等分圆周法;
(2)用尺规等分圆周法.
典题精讲
如图,AD 为⊙O 的直径,作⊙O 的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D 为圆心,OD长为半径画圆弧,交⊙O 于B,C 两点;
(2)连接AB,BC,AC. △ABC 即为所求作的三角形.
乙:(1)作OD 的中垂线,交⊙O 于B,C 两点;
(2)连接AB,AC.△ABC 即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
1
C
典题精讲
在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).
2
解:
如图所示.
(答案不唯一)
易错提醒
一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
A.2 B. C.1 D.
A
易错点:误认为正多边形的边心距是正多边形的半径.
易错提醒
错解:B
诊断:设正多边形的边数为n. 因为正多边形的内角和为(n-2)·180°,正多边形的外角和为360°,根据题意得(n-2)·180°=360°×2,解得n=6,故正多边形为正六边形.边长为2的正六边形可以分成六个边长为2的正三角形,所以正多边形的半径等于2.产生错误的原因是认为正多边形的边心距是正多边形的半径,计算得出错误的结果 ,最后导致错选B.
学以致用
小试牛刀
如图,正六边形ABCDEF 内接于⊙O,若直线PA 与⊙O 相切于点A,则∠PAB 等于( )
A.30°
B.45°
C.150°
D.30°或150°
1
A
小试牛刀
以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
2
D
小试牛刀
如图,⊙O 是正五边形ABCDE 的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R 2-r 2=a 2
B.a=2R sin 36°
C.a=2r tan 36°
D.r=R cos 36°
3
A
小试牛刀
4 如图,点G,H 分别是正六边形ABCDEF 的边BC,CD上的
点,且BG=CH,AG 交BH 于点P.
(1)求证:△ABG ≌ △BCH;
(2)求∠APH 的度数.
(1)证明:∵六边形ABCDEF 为正六边形,∴AB=BC,∠ABC
=∠C=120°.在△ABG 与△BCH 中,
∴△ABG ≌ △BCH.
(2)解:由(1)知△ABG ≌ △BCH,∴∠BAG=∠HBC. ∴∠APH
=∠ABP+∠BAG=∠ABP+∠HBC=∠ABC=120°.
小试牛刀
5 作图与证明:
如图,已知⊙O 和⊙O上的一点A,请完成下列任务:
(1)作⊙O 的内接正六边形ABCDEF;
(2)连接BF,CE,判断四边形BCEF 的形
状并加以证明.
解:(1)如图①,首先作直径AD,然后分别
以A,D 为圆心,OA长为半径画弧,分
别交⊙O 于点B,F,C,E,连接AB,
BC,CD,DE,EF,AF,则正六边形
ABCDEF 即为所求作的图形.
小试牛刀
(2)四边形BCEF 是矩形.
证明:如图②,连接OE. ∵六边形ABCDEF 是正六边形,
∴AB=AF=DE=DC=FE=BC.
∴BF=CE.
∴四边形BCEF 是平行四边形.
∵∠EOD= =60°,OE=OD,
∴△EDO 是等边三角形.∴∠ODE=60°.
∴∠EDC=∠FED=2∠ODE=120°.
∵DE=DC,∴∠DEC=∠DCE=30°.
∴∠CEF=∠DEF-∠DEC=90°.
∴四边形BCEF 是矩形.
小试牛刀
如图,在⊙O 的内接四边形ABCD 中,AB=AD,∠C=120°,
点E 在 上.
(1)求∠AED 的度数;
(2)连接OD,OE,当∠DOE=90°时,AE 恰
好是⊙O 的内接正n 边形的一边,求n 的值.
解:(1)如图,连接BD.∵四边形ABCD 是⊙O 的内接四边形,
∴∠BAD+∠C=180°.∵∠C=120°,∴∠BAD=60°.
∵AB=AD,∴△ABD 是等边三角形.∴∠ABD=60°.
∵四边形ABDE 是⊙O 的内接四边形,
∴∠AED+∠ABD=180°.∴∠AED=120°.
(2)如图,连接OA. ∵∠ABD=60°,∴∠AOD=2∠ABD =120°.
又∵∠DOE=90°,∴∠AOE=∠AOD-∠DOE=30°,
∴n= =12.
小试牛刀
7 如图①、②、③、④分别是⊙O 的内接正三角形、正四边
形、正五边形、正n 边形,点M,N 分别从点B,C 开始以
相同的速度在⊙O 上逆时针运动,AM 与BN 相交于点P.
(1)图①中,∠APN=______;
(2)图②中,∠APN=______,图③中,∠APN=______;
(3)试探索∠APN 的度数与正多边形边数n 的关系(直接写答案).
解:(3)∠APN=
60°
90°
108°
课堂小结
课堂小结
正多边形:各边相等、各角也相等的多边形叫做
正多边形.
把一个圆n (n≥3)等分,顺次连接各等分点,就得
到一个正n 边形. 我们把这个正n 边形叫做圆的内
接正n 边形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
