【班海精品】冀教版(新)九下-29.4 切线长定理 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-29.4 切线长定理 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览









文档简介
(共39张PPT)
29.4 切线长定理
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
什么是切线长定理?
新课精讲
探索新知
1
知识点
三角形内切圆及相关概念
从一块三角形的材料上截下一块圆形的用料,怎样才能使圆的面积尽可能最大呢?
探索新知
作圆:使它和已知三角形的各边都相切
已知:△ABC
求作:和△ABC 的各边都相切的圆
作法:
1、作∠ B,∠ C 的平分线BM 和CN,交点为O
2、过点O 作OD ⊥BC. 垂足为D.
3、以O 为圆心,OD 为半径作圆O.
探索新知
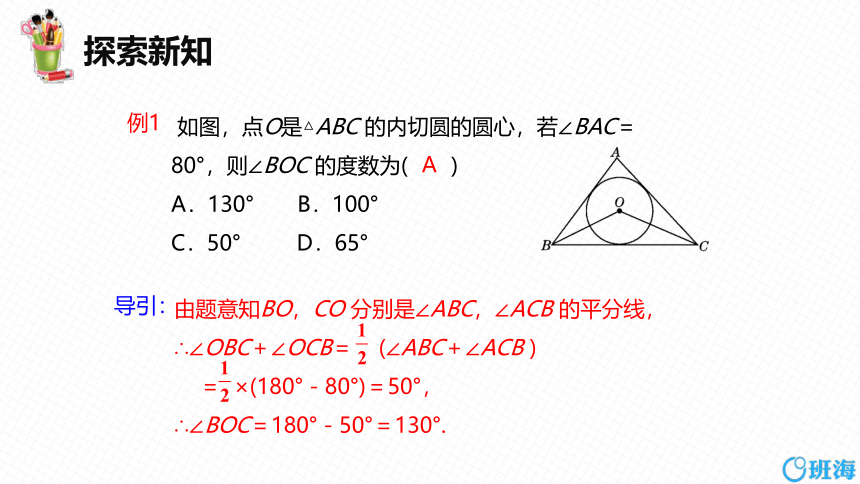
如图,点O是△ABC 的内切圆的圆心,若∠BAC=80°,则∠BOC 的度数为( )
A.130° B.100°
C.50° D.65°
由题意知BO,CO 分别是∠ABC,∠ACB 的平分线,∴∠OBC+∠OCB= (∠ABC+∠ACB )
= ×(180°-80°)=50°,
∴∠BOC=180°-50°=130°.
例1
导引:
A
探索新知
总 结
根据内心的确定方法可知,内心就是三角形三条内角平分线的交点.解决此类问题可以转化为三角形中求两条角平分线的夹角问题.
典题精讲
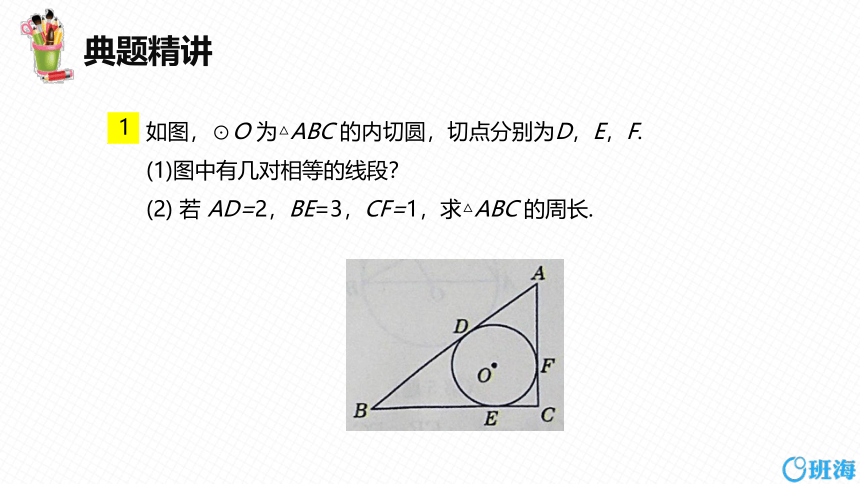
如图,⊙O 为△ABC 的内切圆,切点分别为D,E,F.
(1)图中有几对相等的线段?
(2) 若 AD=2,BE=3,CF=1,求△ABC 的周长.
1
典题精讲
(1)因为⊙O 为△ABC 的内切圆,切点分别为D,
E,F,
所以AD=AF,BD=BE,CE=CF,
所以图中有3对相等的线段.
(2)因为AD=AF,BD=BE,CE=CF,
所以△ABC 的周长=AB+BC+AC
=2(AD+BE+CF )
=2×(2+3+1)=12.
解:
典题精讲
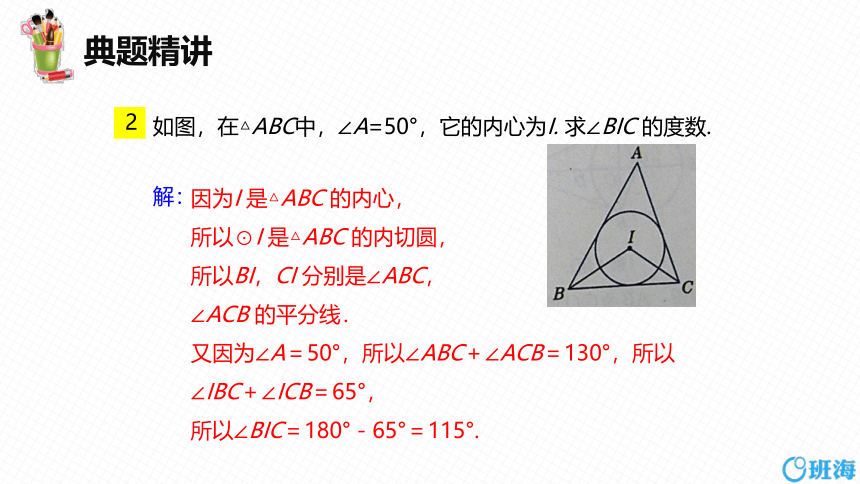
如图,在△ABC中,∠A=50°,它的内心为I. 求∠BIC 的度数.
2
因为I 是△ABC 的内心,
所以⊙I 是△ABC 的内切圆,
所以BI,CI 分别是∠ABC,
∠ACB 的平分线.
又因为∠A=50°,所以∠ABC+∠ACB=130°,所以∠IBC+∠ICB=65°,
所以∠BIC=180°-65°=115°.
解:
典题精讲
下列说法错误的是( )
A.三角形的内切圆与三角形的三边都相切
B.一个三角形一定有唯一一个内切圆
C.一个圆一定有唯一一个外切三角形
D.等边三角形的内切圆与外接圆是同心圆
3
C
典题精讲
如图,⊙O是△ABC 的内切圆,则点O 是△ABC 的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
4
B
典题精讲
如图为4×4的网格图,A,B,C,D,O 均在格点上,点O 是( )
A.△ACD 的外心
B.△ABC 的外心
C.△ACD 的内心
D.△ABC 的内心
5
B
探索新知
2
知识点
三角形内切圆的性质
如图所示,⊙O 是Rt△ABC 的内切圆,切点分别为D,E,F,∠C=90°,AC=3,BC=4,求⊙O 的半径r.
例2
探索新知
连接OA,OB,OC,OD,OE,OF,利用S△ABC=S△COB+S△BOA+S△AOC求解,还可以发现四边形OECD为正方形,则可利用切线长定理,用含r 的代数式表示AB 的长再求解.
导引:
探索新知
方法一:如图,连接OA,OB,OC,OD,OE,OF,则OD=OE=OF=r,OD⊥BC,OE⊥AC,OF⊥AB.
在Rt△ABC 中,AB= =5.
∵S△ABC= S△COB+ S△BOA+ S△AOC,
∴AC·BC=BC·r +AB·r +AC·r
= (BC+AB+AC )·r.
∴r= =1.
解:
探索新知
方法二:如图,连接OD,OE,则OE⊥AC,OD⊥BC,
又∵EC⊥CD,且OE=OD=r,
∴四边形OECD 是正方形.
∴EC=CD=r.
∴AB=AF+BF=AE+BD
=(AC-E C)+(BC-CD )
=3-r+4-r=7-2r.
又易知AB= =5,
∴7-2r=5,即r =1.
典题精讲
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步.问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步(如图),问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
A.3步 B.5步
C.6步 D.8步
1
C
典题精讲
在△ABC 中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A. B.1
C.2 D.
2
B
已知一个三角形的三边长分别为5,7,8,则其内切圆的半径为( )
A. B.
C. D .
3
C
典题精讲
如图,正三角形ABC 的内切圆半径为1,那么这个正三角形的边长为( )
A.2
B.3
C.
D.2
4
D
典题精讲
如图,在矩形ABCD 中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC 和△ADC 的内切圆,则PQ 的长是( )
A.
B.
C.
D.
5
B
易错提示
如图,在△ABC 中,点I 是△ABC 的内心,∠BAC 的平分线和△ABC 的外接圆相交于点D 和BC 交于点E. 求证:DI=DB.
易错点:混淆外心与内心的概念.
易错提示
如图,连接BI.
∵点I 是△ABC 的内心,
∴BI 平分∠ABC. ∴∠ABI=∠CBI.
∵AD 平分∠BAC,∴∠BAD=∠DAC.
∵∠DAC 与∠DBC 均为DC 所对的圆周角,
∴∠DAC=∠DBC.
∴∠ABI+∠BAD=∠CBI+∠DBC,
∴∠BID=∠IBD.
∴DI=DB.
证明:
︵
易错提示
三角形的内心是三角形内切圆的圆心,即三角形三条角平分线的交点;三角形的外心是三角形外接圆的圆心,即三角形三边垂直平分线的交点.本题中既出现了三角形的外接圆,又出现了三角形的内切圆,易混淆三角形的内心与外心的概念,造成证明错误.
易错总结:
学以致用
小试牛刀
下列说法:①三角形的内心不一定在三角形的内部;②若点I 是△ABC 的内心,则AI 平分∠BAC;③三角形有唯一的内切圆,圆有唯一的外切三角形.其中正确的有( )
A.0个 B.1个
C.2个 D.3个
1
B
小试牛刀
如图,在△ABC 中,∠A=66°,点I 是内心,则∠BIC 的大小为( )
A.114°
B.122°
C.123°
D.132°
2
C
小试牛刀
如图,O 是△ABC 的内心,过点O 作EF∥AB,与AC,BC 分别相交于点E,F,则( )
A.EF>AE+BF
B.EF<AE+BF
C.EF=AE+BF
D.EF≤AE+BF
3
C
小试牛刀
如图,以点O 为圆心的圆与△ABC 的三边分别交于点E,
F,G,H,M,N,且EF=GH=MN,求证:点O 是
△ABC 的内心.
证明:如图,过点O 作OD⊥AB 于点D,OP⊥BC 于点P,
OQ⊥AC 于点Q,
连接OE,OF,OG,OH,OM,ON.
∵EF=GH=MN,OE=OF=OG=OH=OM=
ON,∴△OEF ≌ △OGH ≌ △OMN.
∴OD=OP=OQ.
∴点O 是△ABC 的内心.
小试牛刀
证明:(1)∵E 是△ABC 的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC.
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+
∠DBC,∠DBC=∠CAE,
∴∠DBE=∠DEB. ∴DB=DE.
如图,⊙O 是△ABC 的外接圆,BC 为⊙O 的直径,点E 为
△ABC 的内心,连接AE 并延长交⊙O 于D 点,连接BD 并延
长至F,使得DF=BD,连接CF,BE.
(1)求证:DB=DE;
(2)求证:直线CF 为⊙O 的切线.
小试牛刀
(2)如图,连接CD.∵∠DAB=∠DAC,
∴ . ∴BD=CD.
∵BD=DF,∴CD=DB=DF.
∴∠DBC=∠DCB,∠DCF=∠DFC.
∵BC 是⊙O 的直径,
∴∠BDC=90°.
∴∠DBC=∠DCB=∠DCF=∠DFC=45°.
∴∠BCF=90°,
即BC⊥CF.
∴直线CF 是⊙O 的切线.
小试牛刀
已知△ABC 的内切圆⊙O与AB,BC,AC 分别相切于点D,E,F,
若 ,如图①.
(1)判断△ABC 的形状,并证明你的结论;
(2)设AE 与DF 相交于点M,如图②,AF=2FC=4,求AM 的长.
小试牛刀
(1)△ABC 为等腰三角形.
证明:∵△ABC 的内切圆⊙O 与AB,BC,AC 分别
相切于点D,E,F,
∴∠CFO=∠CEO=∠BDO=∠BEO=90°.
∵四边形内角和为360°,
∴∠EOF+∠FCE=180°,
∠DOE+∠DBE=180°.
∵ ,
∴∠EOF=∠DOE.
∴∠FCE=∠DBE. ∴AB=AC.
∴△ABC 为等腰三角形;
解:
小试牛刀
(2)连接OB,OC,OD,OF,如图所示.
易知在等腰三角形ABC 中,AE⊥BC,
∴E 是BC 的中点,即BE=CE.
∵在Rt△AOF 和Rt△AOD 中,
∴Rt△AOF ≌ Rt△AOD. ∴AF=AD,
同理Rt△COF ≌ Rt△COE,CF=CE=2,
Rt△BOD ≌ Rt△BOE,BD=BE.
∴BD=CF,∴DF∥BC. ∴
课堂小结
课堂小结
内切圆:与三角形的三边都相切的圆有且只有一个,我们称这个圆为三角形的内切圆.
内心:内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.4 切线长定理
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
什么是切线长定理?
新课精讲
探索新知
1
知识点
三角形内切圆及相关概念
从一块三角形的材料上截下一块圆形的用料,怎样才能使圆的面积尽可能最大呢?
探索新知
作圆:使它和已知三角形的各边都相切
已知:△ABC
求作:和△ABC 的各边都相切的圆
作法:
1、作∠ B,∠ C 的平分线BM 和CN,交点为O
2、过点O 作OD ⊥BC. 垂足为D.
3、以O 为圆心,OD 为半径作圆O.
探索新知
如图,点O是△ABC 的内切圆的圆心,若∠BAC=80°,则∠BOC 的度数为( )
A.130° B.100°
C.50° D.65°
由题意知BO,CO 分别是∠ABC,∠ACB 的平分线,∴∠OBC+∠OCB= (∠ABC+∠ACB )
= ×(180°-80°)=50°,
∴∠BOC=180°-50°=130°.
例1
导引:
A
探索新知
总 结
根据内心的确定方法可知,内心就是三角形三条内角平分线的交点.解决此类问题可以转化为三角形中求两条角平分线的夹角问题.
典题精讲
如图,⊙O 为△ABC 的内切圆,切点分别为D,E,F.
(1)图中有几对相等的线段?
(2) 若 AD=2,BE=3,CF=1,求△ABC 的周长.
1
典题精讲
(1)因为⊙O 为△ABC 的内切圆,切点分别为D,
E,F,
所以AD=AF,BD=BE,CE=CF,
所以图中有3对相等的线段.
(2)因为AD=AF,BD=BE,CE=CF,
所以△ABC 的周长=AB+BC+AC
=2(AD+BE+CF )
=2×(2+3+1)=12.
解:
典题精讲
如图,在△ABC中,∠A=50°,它的内心为I. 求∠BIC 的度数.
2
因为I 是△ABC 的内心,
所以⊙I 是△ABC 的内切圆,
所以BI,CI 分别是∠ABC,
∠ACB 的平分线.
又因为∠A=50°,所以∠ABC+∠ACB=130°,所以∠IBC+∠ICB=65°,
所以∠BIC=180°-65°=115°.
解:
典题精讲
下列说法错误的是( )
A.三角形的内切圆与三角形的三边都相切
B.一个三角形一定有唯一一个内切圆
C.一个圆一定有唯一一个外切三角形
D.等边三角形的内切圆与外接圆是同心圆
3
C
典题精讲
如图,⊙O是△ABC 的内切圆,则点O 是△ABC 的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
4
B
典题精讲
如图为4×4的网格图,A,B,C,D,O 均在格点上,点O 是( )
A.△ACD 的外心
B.△ABC 的外心
C.△ACD 的内心
D.△ABC 的内心
5
B
探索新知
2
知识点
三角形内切圆的性质
如图所示,⊙O 是Rt△ABC 的内切圆,切点分别为D,E,F,∠C=90°,AC=3,BC=4,求⊙O 的半径r.
例2
探索新知
连接OA,OB,OC,OD,OE,OF,利用S△ABC=S△COB+S△BOA+S△AOC求解,还可以发现四边形OECD为正方形,则可利用切线长定理,用含r 的代数式表示AB 的长再求解.
导引:
探索新知
方法一:如图,连接OA,OB,OC,OD,OE,OF,则OD=OE=OF=r,OD⊥BC,OE⊥AC,OF⊥AB.
在Rt△ABC 中,AB= =5.
∵S△ABC= S△COB+ S△BOA+ S△AOC,
∴AC·BC=BC·r +AB·r +AC·r
= (BC+AB+AC )·r.
∴r= =1.
解:
探索新知
方法二:如图,连接OD,OE,则OE⊥AC,OD⊥BC,
又∵EC⊥CD,且OE=OD=r,
∴四边形OECD 是正方形.
∴EC=CD=r.
∴AB=AF+BF=AE+BD
=(AC-E C)+(BC-CD )
=3-r+4-r=7-2r.
又易知AB= =5,
∴7-2r=5,即r =1.
典题精讲
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步.问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步(如图),问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
A.3步 B.5步
C.6步 D.8步
1
C
典题精讲
在△ABC 中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是( )
A. B.1
C.2 D.
2
B
已知一个三角形的三边长分别为5,7,8,则其内切圆的半径为( )
A. B.
C. D .
3
C
典题精讲
如图,正三角形ABC 的内切圆半径为1,那么这个正三角形的边长为( )
A.2
B.3
C.
D.2
4
D
典题精讲
如图,在矩形ABCD 中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC 和△ADC 的内切圆,则PQ 的长是( )
A.
B.
C.
D.
5
B
易错提示
如图,在△ABC 中,点I 是△ABC 的内心,∠BAC 的平分线和△ABC 的外接圆相交于点D 和BC 交于点E. 求证:DI=DB.
易错点:混淆外心与内心的概念.
易错提示
如图,连接BI.
∵点I 是△ABC 的内心,
∴BI 平分∠ABC. ∴∠ABI=∠CBI.
∵AD 平分∠BAC,∴∠BAD=∠DAC.
∵∠DAC 与∠DBC 均为DC 所对的圆周角,
∴∠DAC=∠DBC.
∴∠ABI+∠BAD=∠CBI+∠DBC,
∴∠BID=∠IBD.
∴DI=DB.
证明:
︵
易错提示
三角形的内心是三角形内切圆的圆心,即三角形三条角平分线的交点;三角形的外心是三角形外接圆的圆心,即三角形三边垂直平分线的交点.本题中既出现了三角形的外接圆,又出现了三角形的内切圆,易混淆三角形的内心与外心的概念,造成证明错误.
易错总结:
学以致用
小试牛刀
下列说法:①三角形的内心不一定在三角形的内部;②若点I 是△ABC 的内心,则AI 平分∠BAC;③三角形有唯一的内切圆,圆有唯一的外切三角形.其中正确的有( )
A.0个 B.1个
C.2个 D.3个
1
B
小试牛刀
如图,在△ABC 中,∠A=66°,点I 是内心,则∠BIC 的大小为( )
A.114°
B.122°
C.123°
D.132°
2
C
小试牛刀
如图,O 是△ABC 的内心,过点O 作EF∥AB,与AC,BC 分别相交于点E,F,则( )
A.EF>AE+BF
B.EF<AE+BF
C.EF=AE+BF
D.EF≤AE+BF
3
C
小试牛刀
如图,以点O 为圆心的圆与△ABC 的三边分别交于点E,
F,G,H,M,N,且EF=GH=MN,求证:点O 是
△ABC 的内心.
证明:如图,过点O 作OD⊥AB 于点D,OP⊥BC 于点P,
OQ⊥AC 于点Q,
连接OE,OF,OG,OH,OM,ON.
∵EF=GH=MN,OE=OF=OG=OH=OM=
ON,∴△OEF ≌ △OGH ≌ △OMN.
∴OD=OP=OQ.
∴点O 是△ABC 的内心.
小试牛刀
证明:(1)∵E 是△ABC 的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC.
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+
∠DBC,∠DBC=∠CAE,
∴∠DBE=∠DEB. ∴DB=DE.
如图,⊙O 是△ABC 的外接圆,BC 为⊙O 的直径,点E 为
△ABC 的内心,连接AE 并延长交⊙O 于D 点,连接BD 并延
长至F,使得DF=BD,连接CF,BE.
(1)求证:DB=DE;
(2)求证:直线CF 为⊙O 的切线.
小试牛刀
(2)如图,连接CD.∵∠DAB=∠DAC,
∴ . ∴BD=CD.
∵BD=DF,∴CD=DB=DF.
∴∠DBC=∠DCB,∠DCF=∠DFC.
∵BC 是⊙O 的直径,
∴∠BDC=90°.
∴∠DBC=∠DCB=∠DCF=∠DFC=45°.
∴∠BCF=90°,
即BC⊥CF.
∴直线CF 是⊙O 的切线.
小试牛刀
已知△ABC 的内切圆⊙O与AB,BC,AC 分别相切于点D,E,F,
若 ,如图①.
(1)判断△ABC 的形状,并证明你的结论;
(2)设AE 与DF 相交于点M,如图②,AF=2FC=4,求AM 的长.
小试牛刀
(1)△ABC 为等腰三角形.
证明:∵△ABC 的内切圆⊙O 与AB,BC,AC 分别
相切于点D,E,F,
∴∠CFO=∠CEO=∠BDO=∠BEO=90°.
∵四边形内角和为360°,
∴∠EOF+∠FCE=180°,
∠DOE+∠DBE=180°.
∵ ,
∴∠EOF=∠DOE.
∴∠FCE=∠DBE. ∴AB=AC.
∴△ABC 为等腰三角形;
解:
小试牛刀
(2)连接OB,OC,OD,OF,如图所示.
易知在等腰三角形ABC 中,AE⊥BC,
∴E 是BC 的中点,即BE=CE.
∵在Rt△AOF 和Rt△AOD 中,
∴Rt△AOF ≌ Rt△AOD. ∴AF=AD,
同理Rt△COF ≌ Rt△COE,CF=CE=2,
Rt△BOD ≌ Rt△BOE,BD=BE.
∴BD=CF,∴DF∥BC. ∴
课堂小结
课堂小结
内切圆:与三角形的三边都相切的圆有且只有一个,我们称这个圆为三角形的内切圆.
内心:内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
