【班海精品】冀教版(新)九下-30.2 二次函数的图像和性质 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-30.2 二次函数的图像和性质 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览








文档简介
(共42张PPT)
30.2 二次函数的图像和性质
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)一次函数的图象是什么?
一条直线
(2)画函数图象的基本方法与步骤是什么?
列表——描点——连线
(3)研究函数时,主要用什么来了解函数的性质呢?
主要工具是函数的图象
回顾旧知
新课精讲
探索新知
1
知识点
二次函数y =ax 2的图像
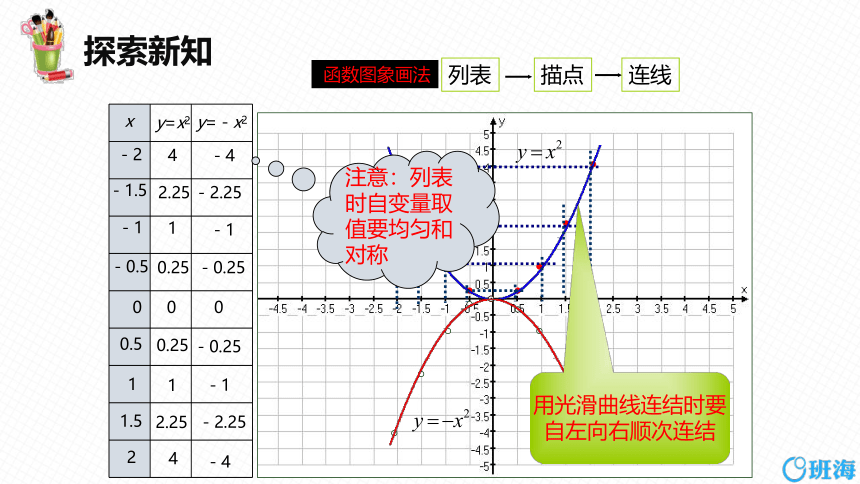
在同一直角坐标系中,画出函数 y = x 2 和 y =-x 2 的图象,这两个函数的图象相比, 有什么共同点?有什么不同点?
探索新知
y=x2
y=-x2
0
0.25
1
2.25
4
0.25
1
2.25
4
0
-0.25
-1
-2.25
-4
-0.25
-1
-2.25
-4
x
0
-2
1
1.5
0.5
2
-1.5
-0.5
-1
函数图象画法
列表
描点
连线
注意:列表
时自变量取
值要均匀和
对称
用光滑曲线连结时要
自左向右顺次连结
探索新知
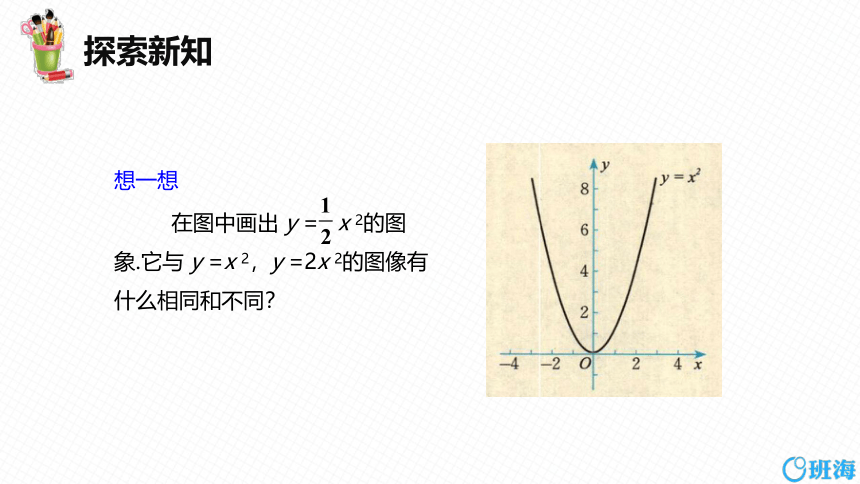
想一想
在图中画出 y = x 2的图
象.它与 y =x 2,y =2x 2的图像有
什么相同和不同?
探索新知
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2
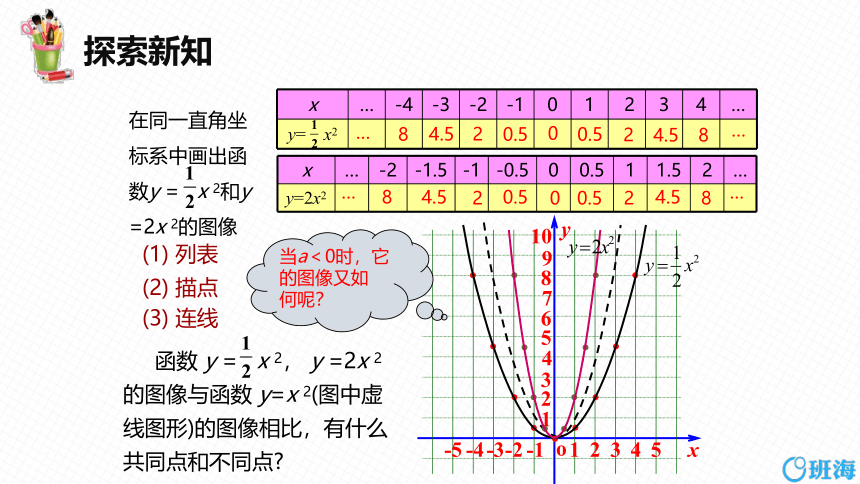
在同一直角坐标系中画出函数y = x 2和y =2x 2的图像
(1) 列表
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
函数 y = x 2, y =2x 2的图像与函数 y=x 2(图中虚线图形)的图像相比,有什么共同点和不同点
当a<0时,它
的图像又如
何呢?
探索新知
归 纳
一般地,抛物线 y=ax 2的对称轴是y 轴,顶点是原点.
当a>0时,抛物线的开口向上,顶点是抛物线的最低点,a 越大,抛物线的开口越小;
当a<0时,抛物线的开口向下,顶点是抛物线的最高点,a 越大,抛物线的开口越大.
不同点:
相同点:
探索新知
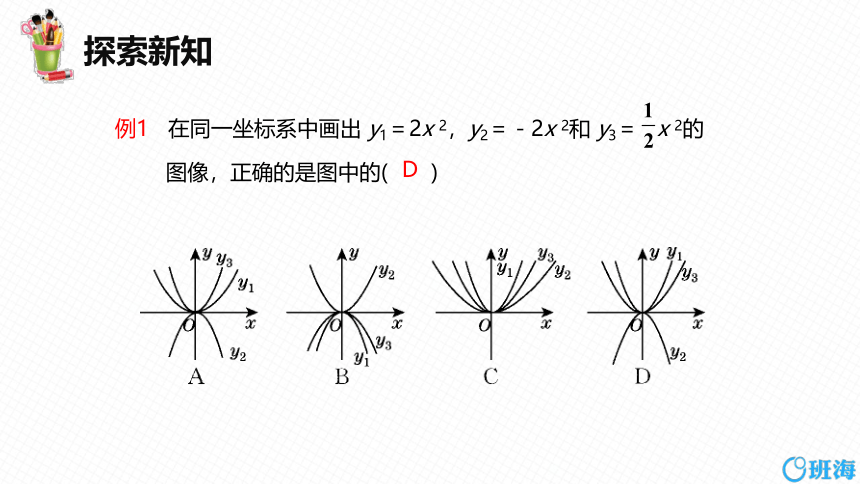
例1 在同一坐标系中画出 y1=2x 2,y2=-2x 2和 y3= x 2的
图像,正确的是图中的( )
D
探索新知
当x=1时, y1, y2, y3的图像上的对应点分别是(1,2),(1,-2), (1, ), 可知,其中有两点在第一象限, 一点在第四象限,排除B,C;在第一象限内,y1的对应点(1,2)在上, y3的对应点(1, )在下,排除A.
导引:
典题精讲
1 关于二次函数y=3x 2的图像,下列说法错误的是( )
A.它是一条抛物线
B.它的开口向上,且关于y 轴对称
C.它的顶点是抛物线的最高点
D.它与y=-3x 2的图像关于x 轴对称
C
若二次函数 y=ax 2的图像过点P (-2,4),则该图像
必经过点( )
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
A
典题精讲
3 关于二次函数 y=2x 2与 y=-2x 2,下列叙述正确的有( )
①它们的图像都是抛物线;
②它们的图像的对称轴都是 y 轴;
③它们的图像都经过点(0,0);
④二次函数 y=2x 2的图像开口向上,二次函数 y=-2x 2的图像
开口向下;
⑤它们的图像关于x 轴对称.
A.5个 B.4个 C.3个 D.2个
A
典题精讲
函数 y=ax-2与y=ax 2(a≠0)在同一平面直角坐标系中的图像可能是( )
4
A
探索新知
2
知识点
二次函数y=ax 2的性质
议一议
观察二次函数y =x 2与 y =-x 2的图象,你能发现什么问题?
探索新知
抛物线
y =x 2
y =-x 2
顶点坐标
对称轴
位置
开口方向
极值
(0,0)
(0,0)
y 轴
y 轴
在x 轴的上方(除顶点外)
在x 轴的下方(除顶点外)
向上
向下
当x =0时,最小值为0.
当x =0时,最大值为0.
探索新知
当a >0时,在对称轴的
左侧,y 随着x 的增大而
减小。
当a>0时,在对称轴的
右侧,y 随着x 的增大而
增大。
当a<0时,在对称轴的
左侧,y 随着x 的增大而
增大。
当a<0时,在对称轴的
右侧,y 随着x 的增大而
减小。
当x=-2时,y=4
当x=-1时,y=1
当x =1时,y =1
当x =2时,y =4
当x=-2时,y =-4
当x=-1时,y =-1
当x =1时,y =-1
当x =2时,y =-4
探索新知
例2 已知函数 y=- x 2,不画图象,回答下列各题.
(1)开口方向:______;
(2)对称轴:_____;
(3)顶点坐标:______;
(4)当x>0时,y 随x 的增大而______;
(5)当x____时,y=0;
(6)当x____时,函数值 y 最____,是___.
导引:根据二次函数 y=ax 2(a≠0)的性质直接作答.
向下
y 轴
减小
(0,0)
=0
=0
大
0
探索新知
例3 已知抛物线y=4x 2过点(x1,y1)和点(x2,y2),当x1<x2<0
时,y1 ________ y2.
导引:方法一:不妨设x1=-2,x2=-1,
将它们分别代入y=4x 2中,得y1=16,
y2=4,所以y1>y2.
方法二:在平面直角坐标系中画出抛
物线 y=4x 2,如图,显然y1>y2.
方法三:因为a=4>0,x1<x2<0,在对称轴的左侧,
y 随x 的增大而减小,所以y1>y2.
>
探索新知
总 结
方法一运用特殊值法,找出符合题目要求的x1和x2的值,计算出对应的y1和y2的值,再比较它们的大小;
方法二运用数形结合思想,根据题意画出图像,利用图象来解题;
方法三运用性质判断法,根据抛物线对应的函数表达式的特点,结合图像的性质进行判断.
典题精讲
不画图像,请指出函数 y=-9x 2图像的开口方向、对称轴、顶点坐标以及最高(或最低)点.
1
开口向下,对称轴为y 轴,顶点坐标为(0,0),最高点为(0,0).
解:
2 若二次函数 y=-ax 2,当x=2时,y= ;则当x=-2时,y=________.
典题精讲
先指出抛物线 y=- x 2的开口方向、对称轴和顶点坐标,然后再画出它的图像.
2
开口向下,对称轴为y 轴,顶点坐标为(0,0).
图像如图.
解:
典题精讲
3 下列关于函数 y=36x 2的叙述中,错误的是( )
A.图像的对称轴是y 轴
B.图像的顶点是原点
C.当x>0时,y 随x 的增大而增大
D.y 有最大值
4 抛物线y= x 2,y=x 2,y=-x 2的共同性质是:
①都是开口向上;②都以点(0,0)为顶点;③都以y 轴为对
称轴;④都关于x 轴对称.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
B
典题精讲
已知抛物线 y=ax 2(a>0)过A (-2,y1),B (1,y2)两点,
则下列关系式一定正确的是( )
A.y1>0>y2
B.y2>0>y1
C.y1>y2>0
D.y2>y1>0
C
易错提醒
已知二次函数 y=x 2,在-1≤x≤4这个范围内,求函数的最值.
易错点:不能准确地掌握二次函数 y=ax 2的图像与性质
易错提醒
当x=-1时,y=(-1)2=1;
当x=4时,y=42=16.
∴在-1≤x≤4这个范围内,函数 y=x 2的最小值是1,最大值是16.
-1≤x≤4时,既包含了正数、零,又包含了负数,因此在这个范围内对应的函数值 y 随x 的变化情况要分段研究.实际上,当x=0时,函数取得最小值0.而x=-1时,y=1;x=4时,
y=16,所以最大值为16.
∵-1≤x≤4包含了x=0,∴函数 y=x 2的最小值为0.当x=-1时,y=1;当x=4时,y=16.
∴当-1≤x≤4时,函数 y=x 2的最大值为16.
错解:
诊断:
正解:
学以致用
小试牛刀
函数 y=k (x-k )与y=k x2,y= (k≠0)在同一平面直角坐标系中的图像可能是( )
1
C
小试牛刀
如图,垂直于x 轴的直线AB 分别与抛物线C1:y=x 2(x ≥0)和抛物线C2:y= (x ≥0)交于A,B 两点,过点A 作CD∥x 轴分别与y 轴和抛物线C2交于点C,D,过点B 作EF∥x 轴分别与y 轴和抛物线C 1交于点E,F,则 的值为( )
B.
C. D.
2
D
小试牛刀
3 对于二次函数:①y=3x 2;②y= x 2;③y= x 2,它们的图像在同一坐标系中,开口大小的顺序用序号来表示应是( )
A.②>③>① B.②>①>③
C.③>①>② D.③>②>①
A
小试牛刀
4 已知函数 y=(m+3)x m 2+3m-2是关于x 的二次函数.
(1)求m 的值.
(2)当m 为何值时,该函数图像的开口向下?
(3)当m 为何值时,该函数有最小值?
解:
(1)根据题意,得
解得
∴m=-4或m=1.
小试牛刀
(2)∵函数图像的开口向下,
∴m+3<0.
∴m<-3.
∴m=-4.
∴当m=-4时,该函数图像的开口向下.
(3)∵函数有最小值,∴m+3>0.
∴m>-3.∴m=1.
∴当m=1时,该函数有最小值.
小试牛刀
5 根据下列条件分别求a 的值或取值范围.
(1)函数 y=(a-2)x 2,当x>0时,y 随x 的增大而减小,
当x<0时,y 随x 的增大而增大;
(2)函数 y=(3a-2)x 2有最大值;
(3)抛物线 y=(a+2)x 2与抛物线y=- x 2的形状相同;
(4)函数 y=axa 2+a 的图像是开口向上的抛物线.
小试牛刀
(1)由题意得a-2<0,解得a<2.
(2)由题意得3a-2<0,解得a< .
(3)由题意得|a+2|= ,
解得a1=- ,a2=- .
(4)由题意得a 2+a=2,解得a1=-2,a2=1.
又由题意知a>0,∴a=1.
解:
小试牛刀
已知一次函数 y=kx+b 与二次函数 y=ax 2的图像如图所示,
其中一次函数的图像与x 轴,y 轴的交点分别为A (2,0),B
(0,2),直线与抛物线的交点分别为P,Q,且它们的纵坐标
的比为1∶4,求这两个函数的表达式.
小试牛刀
解:
把点A的坐标(2,0)和点B的坐标(0,2)分别代入 y=kx+b,
得 解得 ∴一次函数的表达式为 y=-x+2.
设点P 的坐标为(x1,y1),点Q 的坐标为(x2,y2),则y1∶y2=
1∶4,∴y2=4y1,即ax12?ax22=1∶4.
又点Q 在第二象限,点P 在第一象限,∴x1∶x2=-1∶2.
∴x2=-2x1. ∴点Q 的坐标为(-2x1,4y1).
把P,Q 两点的坐标分别代入y=-x+2,
得 解得
∴点P 的坐标为(1,1).把点P 的坐标(1,1)代入 y=ax 2,
得a=1. ∴二次函数的表达式为 y=x 2.
小试牛刀
如图,抛物线 y=ax 2与直线 y=kx+b 在第一象限内交于点
A(2,4).
(1)求抛物线对应的函数表达式.
(2)在x 轴上是否存在一点P,使 △AOP 为等腰三角形?
若存在,请你求出点P 的坐标;若不存在,请说明理由.
解:
(1)将A(2,4)的坐标代入 y=ax 2得4=4a,∴a=1.
∴抛物线表达式为 y=x 2.
小试牛刀
(2)设有一点P (x,0)使△AOP 为等腰三角形.
由题意知OA= =2 .
当OA=OP 时,OP=2 ,
∴P (2 ,0)或 P (-2 ,0).
当OA=AP 时,(x-2)2+16=20,
∴x=0(舍去)或 x=4. ∴P (4,0).
当OP=AP 时,x 2=(x-2)2+16,
∴x=5. ∴P (5,0).
∴当点P 的坐标为(2 ,0),(-2 ,0),(4,0)或
(5,0)时,△AOP 为等腰三角形.
课堂小结
课堂小结
1. 画函数图像的步骤有哪些?
2. 二次函数 y =ax 2的图像有哪些性质?
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
30.2 二次函数的图像和性质
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)一次函数的图象是什么?
一条直线
(2)画函数图象的基本方法与步骤是什么?
列表——描点——连线
(3)研究函数时,主要用什么来了解函数的性质呢?
主要工具是函数的图象
回顾旧知
新课精讲
探索新知
1
知识点
二次函数y =ax 2的图像
在同一直角坐标系中,画出函数 y = x 2 和 y =-x 2 的图象,这两个函数的图象相比, 有什么共同点?有什么不同点?
探索新知
y=x2
y=-x2
0
0.25
1
2.25
4
0.25
1
2.25
4
0
-0.25
-1
-2.25
-4
-0.25
-1
-2.25
-4
x
0
-2
1
1.5
0.5
2
-1.5
-0.5
-1
函数图象画法
列表
描点
连线
注意:列表
时自变量取
值要均匀和
对称
用光滑曲线连结时要
自左向右顺次连结
探索新知
想一想
在图中画出 y = x 2的图
象.它与 y =x 2,y =2x 2的图像有
什么相同和不同?
探索新知
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2
在同一直角坐标系中画出函数y = x 2和y =2x 2的图像
(1) 列表
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
函数 y = x 2, y =2x 2的图像与函数 y=x 2(图中虚线图形)的图像相比,有什么共同点和不同点
当a<0时,它
的图像又如
何呢?
探索新知
归 纳
一般地,抛物线 y=ax 2的对称轴是y 轴,顶点是原点.
当a>0时,抛物线的开口向上,顶点是抛物线的最低点,a 越大,抛物线的开口越小;
当a<0时,抛物线的开口向下,顶点是抛物线的最高点,a 越大,抛物线的开口越大.
不同点:
相同点:
探索新知
例1 在同一坐标系中画出 y1=2x 2,y2=-2x 2和 y3= x 2的
图像,正确的是图中的( )
D
探索新知
当x=1时, y1, y2, y3的图像上的对应点分别是(1,2),(1,-2), (1, ), 可知,其中有两点在第一象限, 一点在第四象限,排除B,C;在第一象限内,y1的对应点(1,2)在上, y3的对应点(1, )在下,排除A.
导引:
典题精讲
1 关于二次函数y=3x 2的图像,下列说法错误的是( )
A.它是一条抛物线
B.它的开口向上,且关于y 轴对称
C.它的顶点是抛物线的最高点
D.它与y=-3x 2的图像关于x 轴对称
C
若二次函数 y=ax 2的图像过点P (-2,4),则该图像
必经过点( )
A.(2,4) B.(-2,-4)
C.(-4,2) D.(4,-2)
A
典题精讲
3 关于二次函数 y=2x 2与 y=-2x 2,下列叙述正确的有( )
①它们的图像都是抛物线;
②它们的图像的对称轴都是 y 轴;
③它们的图像都经过点(0,0);
④二次函数 y=2x 2的图像开口向上,二次函数 y=-2x 2的图像
开口向下;
⑤它们的图像关于x 轴对称.
A.5个 B.4个 C.3个 D.2个
A
典题精讲
函数 y=ax-2与y=ax 2(a≠0)在同一平面直角坐标系中的图像可能是( )
4
A
探索新知
2
知识点
二次函数y=ax 2的性质
议一议
观察二次函数y =x 2与 y =-x 2的图象,你能发现什么问题?
探索新知
抛物线
y =x 2
y =-x 2
顶点坐标
对称轴
位置
开口方向
极值
(0,0)
(0,0)
y 轴
y 轴
在x 轴的上方(除顶点外)
在x 轴的下方(除顶点外)
向上
向下
当x =0时,最小值为0.
当x =0时,最大值为0.
探索新知
当a >0时,在对称轴的
左侧,y 随着x 的增大而
减小。
当a>0时,在对称轴的
右侧,y 随着x 的增大而
增大。
当a<0时,在对称轴的
左侧,y 随着x 的增大而
增大。
当a<0时,在对称轴的
右侧,y 随着x 的增大而
减小。
当x=-2时,y=4
当x=-1时,y=1
当x =1时,y =1
当x =2时,y =4
当x=-2时,y =-4
当x=-1时,y =-1
当x =1时,y =-1
当x =2时,y =-4
探索新知
例2 已知函数 y=- x 2,不画图象,回答下列各题.
(1)开口方向:______;
(2)对称轴:_____;
(3)顶点坐标:______;
(4)当x>0时,y 随x 的增大而______;
(5)当x____时,y=0;
(6)当x____时,函数值 y 最____,是___.
导引:根据二次函数 y=ax 2(a≠0)的性质直接作答.
向下
y 轴
减小
(0,0)
=0
=0
大
0
探索新知
例3 已知抛物线y=4x 2过点(x1,y1)和点(x2,y2),当x1<x2<0
时,y1 ________ y2.
导引:方法一:不妨设x1=-2,x2=-1,
将它们分别代入y=4x 2中,得y1=16,
y2=4,所以y1>y2.
方法二:在平面直角坐标系中画出抛
物线 y=4x 2,如图,显然y1>y2.
方法三:因为a=4>0,x1<x2<0,在对称轴的左侧,
y 随x 的增大而减小,所以y1>y2.
>
探索新知
总 结
方法一运用特殊值法,找出符合题目要求的x1和x2的值,计算出对应的y1和y2的值,再比较它们的大小;
方法二运用数形结合思想,根据题意画出图像,利用图象来解题;
方法三运用性质判断法,根据抛物线对应的函数表达式的特点,结合图像的性质进行判断.
典题精讲
不画图像,请指出函数 y=-9x 2图像的开口方向、对称轴、顶点坐标以及最高(或最低)点.
1
开口向下,对称轴为y 轴,顶点坐标为(0,0),最高点为(0,0).
解:
2 若二次函数 y=-ax 2,当x=2时,y= ;则当x=-2时,y=________.
典题精讲
先指出抛物线 y=- x 2的开口方向、对称轴和顶点坐标,然后再画出它的图像.
2
开口向下,对称轴为y 轴,顶点坐标为(0,0).
图像如图.
解:
典题精讲
3 下列关于函数 y=36x 2的叙述中,错误的是( )
A.图像的对称轴是y 轴
B.图像的顶点是原点
C.当x>0时,y 随x 的增大而增大
D.y 有最大值
4 抛物线y= x 2,y=x 2,y=-x 2的共同性质是:
①都是开口向上;②都以点(0,0)为顶点;③都以y 轴为对
称轴;④都关于x 轴对称.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
B
典题精讲
已知抛物线 y=ax 2(a>0)过A (-2,y1),B (1,y2)两点,
则下列关系式一定正确的是( )
A.y1>0>y2
B.y2>0>y1
C.y1>y2>0
D.y2>y1>0
C
易错提醒
已知二次函数 y=x 2,在-1≤x≤4这个范围内,求函数的最值.
易错点:不能准确地掌握二次函数 y=ax 2的图像与性质
易错提醒
当x=-1时,y=(-1)2=1;
当x=4时,y=42=16.
∴在-1≤x≤4这个范围内,函数 y=x 2的最小值是1,最大值是16.
-1≤x≤4时,既包含了正数、零,又包含了负数,因此在这个范围内对应的函数值 y 随x 的变化情况要分段研究.实际上,当x=0时,函数取得最小值0.而x=-1时,y=1;x=4时,
y=16,所以最大值为16.
∵-1≤x≤4包含了x=0,∴函数 y=x 2的最小值为0.当x=-1时,y=1;当x=4时,y=16.
∴当-1≤x≤4时,函数 y=x 2的最大值为16.
错解:
诊断:
正解:
学以致用
小试牛刀
函数 y=k (x-k )与y=k x2,y= (k≠0)在同一平面直角坐标系中的图像可能是( )
1
C
小试牛刀
如图,垂直于x 轴的直线AB 分别与抛物线C1:y=x 2(x ≥0)和抛物线C2:y= (x ≥0)交于A,B 两点,过点A 作CD∥x 轴分别与y 轴和抛物线C2交于点C,D,过点B 作EF∥x 轴分别与y 轴和抛物线C 1交于点E,F,则 的值为( )
B.
C. D.
2
D
小试牛刀
3 对于二次函数:①y=3x 2;②y= x 2;③y= x 2,它们的图像在同一坐标系中,开口大小的顺序用序号来表示应是( )
A.②>③>① B.②>①>③
C.③>①>② D.③>②>①
A
小试牛刀
4 已知函数 y=(m+3)x m 2+3m-2是关于x 的二次函数.
(1)求m 的值.
(2)当m 为何值时,该函数图像的开口向下?
(3)当m 为何值时,该函数有最小值?
解:
(1)根据题意,得
解得
∴m=-4或m=1.
小试牛刀
(2)∵函数图像的开口向下,
∴m+3<0.
∴m<-3.
∴m=-4.
∴当m=-4时,该函数图像的开口向下.
(3)∵函数有最小值,∴m+3>0.
∴m>-3.∴m=1.
∴当m=1时,该函数有最小值.
小试牛刀
5 根据下列条件分别求a 的值或取值范围.
(1)函数 y=(a-2)x 2,当x>0时,y 随x 的增大而减小,
当x<0时,y 随x 的增大而增大;
(2)函数 y=(3a-2)x 2有最大值;
(3)抛物线 y=(a+2)x 2与抛物线y=- x 2的形状相同;
(4)函数 y=axa 2+a 的图像是开口向上的抛物线.
小试牛刀
(1)由题意得a-2<0,解得a<2.
(2)由题意得3a-2<0,解得a< .
(3)由题意得|a+2|= ,
解得a1=- ,a2=- .
(4)由题意得a 2+a=2,解得a1=-2,a2=1.
又由题意知a>0,∴a=1.
解:
小试牛刀
已知一次函数 y=kx+b 与二次函数 y=ax 2的图像如图所示,
其中一次函数的图像与x 轴,y 轴的交点分别为A (2,0),B
(0,2),直线与抛物线的交点分别为P,Q,且它们的纵坐标
的比为1∶4,求这两个函数的表达式.
小试牛刀
解:
把点A的坐标(2,0)和点B的坐标(0,2)分别代入 y=kx+b,
得 解得 ∴一次函数的表达式为 y=-x+2.
设点P 的坐标为(x1,y1),点Q 的坐标为(x2,y2),则y1∶y2=
1∶4,∴y2=4y1,即ax12?ax22=1∶4.
又点Q 在第二象限,点P 在第一象限,∴x1∶x2=-1∶2.
∴x2=-2x1. ∴点Q 的坐标为(-2x1,4y1).
把P,Q 两点的坐标分别代入y=-x+2,
得 解得
∴点P 的坐标为(1,1).把点P 的坐标(1,1)代入 y=ax 2,
得a=1. ∴二次函数的表达式为 y=x 2.
小试牛刀
如图,抛物线 y=ax 2与直线 y=kx+b 在第一象限内交于点
A(2,4).
(1)求抛物线对应的函数表达式.
(2)在x 轴上是否存在一点P,使 △AOP 为等腰三角形?
若存在,请你求出点P 的坐标;若不存在,请说明理由.
解:
(1)将A(2,4)的坐标代入 y=ax 2得4=4a,∴a=1.
∴抛物线表达式为 y=x 2.
小试牛刀
(2)设有一点P (x,0)使△AOP 为等腰三角形.
由题意知OA= =2 .
当OA=OP 时,OP=2 ,
∴P (2 ,0)或 P (-2 ,0).
当OA=AP 时,(x-2)2+16=20,
∴x=0(舍去)或 x=4. ∴P (4,0).
当OP=AP 时,x 2=(x-2)2+16,
∴x=5. ∴P (5,0).
∴当点P 的坐标为(2 ,0),(-2 ,0),(4,0)或
(5,0)时,△AOP 为等腰三角形.
课堂小结
课堂小结
1. 画函数图像的步骤有哪些?
2. 二次函数 y =ax 2的图像有哪些性质?
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
