【班海精品】冀教版(新)九下-30.4 二次函数的应用 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-30.4 二次函数的应用 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览






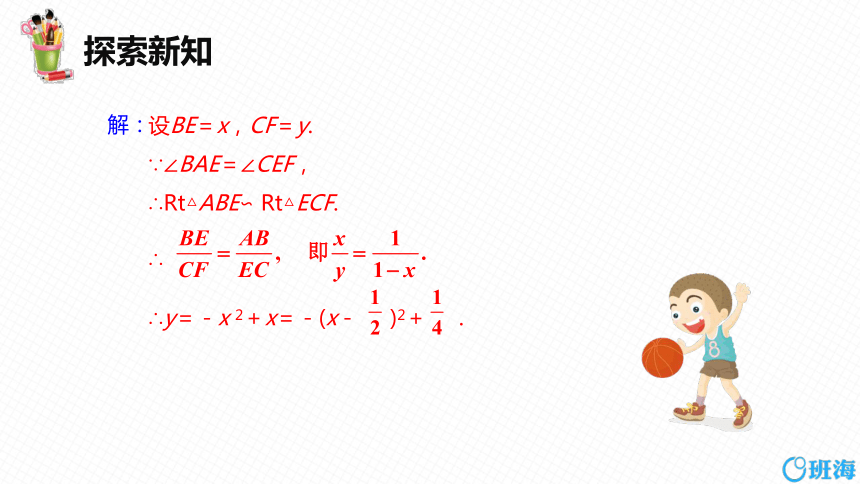



文档简介
(共45张PPT)
30.4 二次函数的应用
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们去商场买衣服时,售货员一般都鼓励顾客多买,这样可以给顾客打折或降价,相应的每件的利润就少了,但是老板的收入会受到影响吗?怎样调整价格才能让利益最大化呢?通过本课的学习,我们就可以解决这些问题.
新课精讲
探索新知
1
知识点
用二次函数表示实际问题
根据实际问题列二次函数的关系式,一般要经历以下几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关系
列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
探索新知
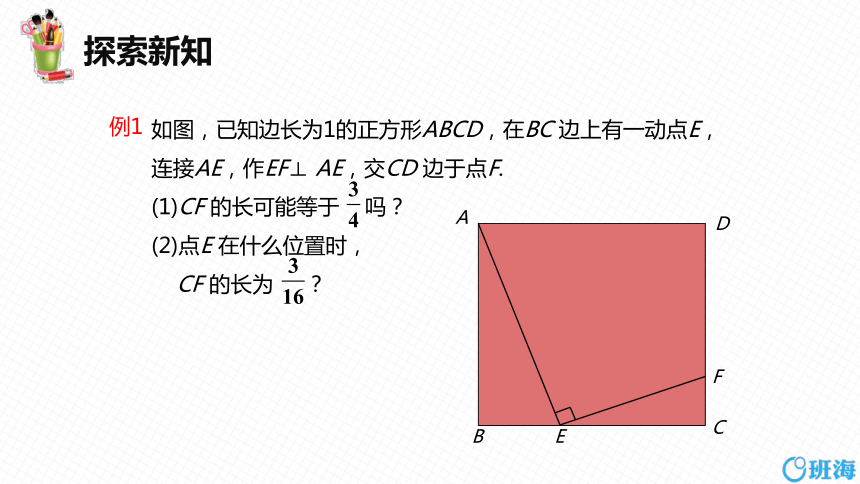
如图,已知边长为1的正方形ABCD,在BC 边上有一动点E,连接AE,作EF⊥ AE,交CD 边于点F.
(1)CF 的长可能等于 吗?
(2)点E 在什么位置时,
CF 的长为 ?
例1
A
D
F
C
E
B
探索新知
设BE=x,CF=y.
∵∠BAE=∠CEF,
∴Rt△ABE∽ Rt△ECF.
∴
∴y=-x 2+x=-(x- )2+ .
解:
探索新知
∵ y最大= ,
∴ CF 的长不可能等于 .
(2)设-x 2+x= 即16x 2-16x+3=0.
解得x1= ,x2=
∴当BE 的长为 或 时,均有CF 的长为 .
典题精讲
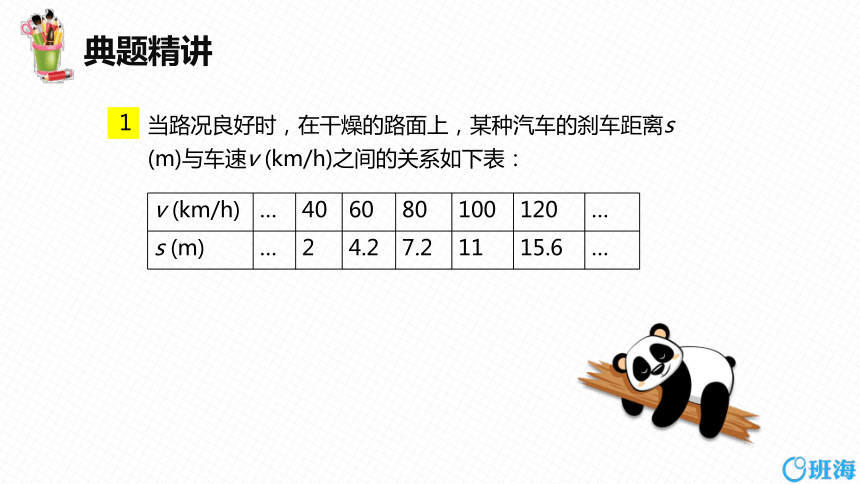
当路况良好时,在干燥的路面上,某种汽车的刹车距离s (m)与车速v (km/h)之间的关系如下表:
1
v (km/h) … 40 60 80 100 120 …
s (m) … 2 4.2 7.2 11 15.6 …
典题精讲
(1)在平面直角坐标系中描出每对(v,s)所对应的点,并用平滑的曲线顺次连接各点.
解:(1)如图.
典题精讲
(2)利用图像验证刹车距离众s(m)与车速v(km/h)是否具有
如下关系:
解:分别令v=40 km/h,60 km/h,80 km/h,100 km/h,
120 km/h,由
分别可得s=2 m,4.2 m,7.2 m,11 m,15.6 m.
∴刹车距离s (m)与车速v (km/h)
具有 的关系.
典题精讲
(3)求s=9 m时的车速v.
解:令s=9 m,则
解得v1=-100(km/h)(舍去),v2=90(km/h).
∴当s=9 m时,车速v=90 km/h.
典题精讲
某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a 元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t (t 为正整数)的增大而增大,a 的取值范围应为_____________.
2
0<a<6
探索新知
2
知识点
利用二次函数的最值解实际问题
利用二次函数解决实际生活中的利润问题,一般运用“总利润=每件商品所获利润×销售件数”或“总利润=总售价-总成本”建立利润与销售单价之间的二次函数关系式,求其图象的顶点坐标,获取最值.
探索新知
例2 某旅馆有客房120间,每间房的日租金为160元时,每天都客满.
经市场调查发现,如果每间客房的日租金增加10元,那么客房每
天出租数会减少6间.不考虑其他因素,旅馆将每间客房的日租金
提高到多少元时,客房日租金的总收入最高?最高总收入是多少?
探索新知
设每间客房的日租金提高10x 元,则每天客房出租数会
减少6x 间.设客房日租金总收入为 y 元,
则 y = (160+10x ) (120-6x )= -60 (x-2)2+ 19 440.
∵x ≥0,且120-6x >0,∴0≤x< 20.
当x =2时,y最大= 19 440.
这时每间客房的日租金为160 +10×2=180 (元).
因此,每间客房的日租金提高到180元时,客房总收人
最高,最高收入为 19 440 元.
解:
探索新知
例3 一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量
为2万件.今年计划通过适当增加成本来提高产品的档次,以拓展市场,若今
年这种玩具每件的成本比去年每件的成本增加0.7x 倍,今年这种玩具每件的出
厂价比去年每件的出厂价相应提高0.5x 倍,则预计今年年销售量将比去年年销
售量增加x 倍(0<x≤1).
(1)用含x 的代数式表示:今年生产的这种玩具每件的成本为___元,今年生产的
这种玩具每件的出厂价为____元;
(2)求今年这种玩具每件的利润y (元)与x 之间的函数关系式;
(3)设今年这种玩具的年销售利润为W 万元,求当x 为何值时,今年的年销售利
润最大,最大年销售利润是多少万元?
探索新知
由题意知今年这种玩具每件的成本是去年的(1+0.7x )倍,每件的
出厂价是去年每件的出厂价的 (1+0.5x )倍,今年的年销售量是去
年年销售量的 (1+x )倍.
解:(1)(10+7x );(12+6x )
(2)y=(12+6x )-(10+7x )=2-x,
即y 与x 的函数关系式为 y=2-x.
(3)W=2(1+x )(2-x )=-2x 2+2x+4=-2(x-5)2+4.5,
∵0<x≤1,∴当x=0.5时,W 有最大值.
W最大值=4.5.
答:当x=0.5时,今年的年销售利润最大,最大年销
售利润为4.5万元.
导引:
探索新知
总 结
本题利用建模思想求解,由今年与去年这种玩具的成本价、出厂价、销售量的倍数关系可以得到今年这种玩具的成本价、出厂价、销售量的表达式,再由“总利润=每件商品所获利润×销售件数”可得二次函数的表达式,进而求出其最大值.
典题精讲
1 某旅行社在五一期间接团去外地旅游,经计算,收益y (元)与旅行团人数x (人)满足表达式y=-x 2+100x+28 400,要使收益最大,则此旅行团应有( )
A.30人 B.40人
C.50人 D.55人
C
典题精讲
某网店销售某款童装,每件售价60元,每星期可卖300件,为了
促销,该网店决定降价销售.市场调查反映:每降价1元,每星期
可多卖30件.已知该款童装每件成本价40元,设该款童装每件售
价x 元,每星期的销售量为y 件.
(1)求y 与x 之间的函数表达式.
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润
是多少元?
(3)若该网店每星期想要获得不低于6 480元的利润,每星期至少
要销售该款童装多少件?
典题精讲
(1) y=300+30(60-x )=-30x+2 100.
(2)设每星期的销售利润为W 元,
则W=(x-40)(-30x+2 100)
=-30(x-55)2+6 750.
∴当x=55时,W 取最大值为6 750.
∴每件售价定为55元时,每星期的销售利润最大,
最大利润为6 750元.
解:
典题精讲
(3)由题意得(x-40)(-30x+2 100)≥6 480,
解得52≤x≤58.
当x=52时,销售量为300+30×8=540(件),
当x=58时,销售量为300+30×2=360(件),
∴该网店每星期想要获得不低于6 480元的利润,
每星期至少要销售该款童装360件.
易错提醒
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y (kg)与销售单价x (元)符合一次函数关系,如图是 y 与x 的函数关系图象.
易错提醒
(1)求 y 与x 的函数表达式;
(2)设该水果销售店试销草莓获得的利润为W 元,求W 的最大值.
易错点:将销售额当销售利润而致错
易错提醒
(1)设y 与x 的函数表达式为 y=kx+b,
根据题意,得
解得
∴y 与x 的函数表达式为 y=-2x+340(20≤x≤40).
解:
k=-2,
b=340.
20k+b=300,
30k+b=280.
易错提醒
(2)由已知得W=(x-20)(-2x+340)
=-2x 2+380x-6 800
=-2(x-95)2+11 250,
∵-2<0,
∴当x≤95时,W 随x 的增大而增大.
∵20≤x≤40,
∴当x=40时,W 最大,
最大值为-2×(40-95)2+11 250=5 200.
学以致用
小试牛刀
1 在一幅长60 cm,宽40 cm的矩形油画的四周镶一条金色
纸边,制成一幅矩形挂图,如图所示,如果要使整幅挂图
的面积是 y cm2,设金色纸边的宽度为x cm,那么 y 关
于x 的函数表达式是( )
A.y=(60+2x )(40+2x )
B.y=(60+x )(40+x )
C.y=(60+2x )(40+x )
D.y=(60+x )(40+2x )
A
2 心理学家发现:学生对概念的接受能力y 与提出概念的时间
x (min)之间是二次函数关系,当提出概念13min时,学生对
概念的接受能力最大,为59.9;当提出概念30 min时,学生
对概念的接受能力就剩下31,则 y 与x 满足的二次函数表达
式为( )
A.y=-(x-13)2+59.9
B.y=-0.1x 2+2.6x+31
C.y=0.1x 2-2.6x+76.8
D.y=-0.1x 2+2.6x+43
D
小试牛刀
小试牛刀
随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的
选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,
C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点
与文化宫距离为x (单位:km),乘坐地铁的时间y1(单位:min)是关于
x 的一次函数,其关系如下表:
地铁站 A B C D E
x/km 8 9 10 11.5 13
y1/min 18 20 22 25 28
小试牛刀
解:
(1)求y1关于x 的函数表达式;
(2)李华骑单车的时间(单位:min)也受x 的影响,其关系
可用y2= x 2-11x+78来描述,请问:李华应选择在
哪一站出地铁,才能使他从文化宫回到家所需的时间
最短?并求出最短时间.
(1)设y1=kx+b,将(8,18),(9,20)的坐标代入,
得 解得
故y1关于x 的函数表达式为y1=2x+2.
小试牛刀
(2)设李华从文化宫回到家所需的时间为y (单位:min),
则 y=y1+y2=2x+2+ x 2-11x+78= x 2-9x+80,
∴当x=9时,y 有最小值,ymin= =39.5.
答:李华应选择在B 站出地铁,才能使他从文化宫回到家所需的时
间最短,最短时间为39.5 min.
小试牛刀
某水果店在两周内,将标价为10元/斤的某种水果,经过两次降
价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x 天(x 为整数)的售价、销量及
储存和损耗费用的相关信息如下表所示.已知该种水果的进价
为4.1元/斤,设销售该水果第x 天的利润为y 元,求y 与x
(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
小试牛刀
时间x/天 1≤x<9 9≤x<15 x≥15
售价/(元/斤) 第1次降价
后的价格 第2次降价
后的价格
销量/斤 80-3x 120-x
储存和损耗
费用/元 40+3x 3x 2-64x+400
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
小试牛刀
(1)设该种水果每次降价的百分率是x,
由题意得10(1-x )2=8.1,
解得x=10%或x=190%(舍去).
答:该种水果每次降价的百分率是10%.
(2)当1≤x<9时,第一次降价后的价格为10×(1-10%)=9(元/斤),
∴y=(9-4.1)(80-3x )-(40+3x )=-17.7x+352.
∵-17.7<0,∴y 随x 的增大而减小,
∴当x=1时,y 有最大值,
y最大值=-17.7×1+352=334.3.
当9≤x<15时,第2次降价后的价格为8.1元/斤,
解:
小试牛刀
∴y=(8.1-4.1)(120-x )-(3x 2-64x+400)
=-3x 2+60x+80=-3(x-10)2+380,
∵-3<0,∴当9≤x≤10时,y 随x 的增大而增大,
当10<x<15时,y 随x 的增大而减小.
∴当x=10时,y 有最大值,y最大值=380.
∵334.3<380,∴当x=10时,y 取最大值.
综上所述,y 与x (1≤x< 15)之间的函数关系式为
y= 第10天时销售利润最大.
(3)设第15天在第14天的价格基础上降a 元,
由题意得380-127.5≤(4-a)×(120-15)-(3×152-64×
15+400),解得a ≤0.5.
答:第15天在第14天的价格基础上最多可降0.5元.
小试牛刀
5 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x 天(1≤x≤90,且x 为整数)的售价与销售量的相关信息如图和下表所示.已知商品的进价为30元/件,设该商品的售价为y (单位:元/件),每天的销售量为p (单位:件),每天的销售利润为w (单位:元).
(1)求出w 与x 的函数表达式.
(2)问销售该商品第几天时,当天的销售
利润最大?并求出最大利润.
(3)该商品在销售过程中,共有多少天每
天的销售利润不低于5 600元?请直接写出结果.
时间x/天 1 30 60 90
每天的销售量p/件 198 140 80 20
小试牛刀
解:
(1)当1≤x≤50时,设商品的售价y 与时间x 的函数表达式为y
=kx+b (k,b 为常数,且k≠0),
根据题意,得
∴ 解得
∴当1≤x≤50时,售价y 与时间x 的函数表达式为y=x+40.
当50<x≤90时,y=90.
∴售价y 与时间x 的函数表达式为
y=
由表格可知,每天的销售量p 与时间x 成一次函数.
小试牛刀
设每天的销售量p 与时间x 的函数表达式为p=mx+n (m,n 为常数,且m≠0),
根据题意,得
∴ 解得
∴p=-2x+200(1≤x≤90,且x 为整数).
当1≤x≤50时,w=(y-30)·p=(x+40-30)(-2x+200)=
-2x 2+180x+2 000;
当50<x≤90时,w=(90-30)·(-2x+200)=-120x+12 000.
综上,每天的销售利润w 与时间x 的函数表达式是
w=
小试牛刀
(2)当1≤x≤50时,
w=-2x 2+180x+2 000=-2(x-45)2+6 050,
∵a=-2<0且1≤x≤50,
∴当x=45时,w 取最大值,最大值为6 050.
当50<x≤90时,w=-120x+12 000,
∵-120<0,
∴w 随x 的增大而减小.∴w<6 000.
综上可知,当x=45时,w 最大,最大值为6 050.
即销售该商品第45天时,当天的销售利润最大,最大
利润是6 050元.
(3)24天.
课堂小结
课堂小结
利润问题的基本关系式:
总利润=单件利润×销售总量.
若销售单价每提高m 元,销售量相应减少n 件,
设提高x 元,则现销售量=原销售量-
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
30.4 二次函数的应用
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们去商场买衣服时,售货员一般都鼓励顾客多买,这样可以给顾客打折或降价,相应的每件的利润就少了,但是老板的收入会受到影响吗?怎样调整价格才能让利益最大化呢?通过本课的学习,我们就可以解决这些问题.
新课精讲
探索新知
1
知识点
用二次函数表示实际问题
根据实际问题列二次函数的关系式,一般要经历以下几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关系
列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
探索新知
如图,已知边长为1的正方形ABCD,在BC 边上有一动点E,连接AE,作EF⊥ AE,交CD 边于点F.
(1)CF 的长可能等于 吗?
(2)点E 在什么位置时,
CF 的长为 ?
例1
A
D
F
C
E
B
探索新知
设BE=x,CF=y.
∵∠BAE=∠CEF,
∴Rt△ABE∽ Rt△ECF.
∴
∴y=-x 2+x=-(x- )2+ .
解:
探索新知
∵ y最大= ,
∴ CF 的长不可能等于 .
(2)设-x 2+x= 即16x 2-16x+3=0.
解得x1= ,x2=
∴当BE 的长为 或 时,均有CF 的长为 .
典题精讲
当路况良好时,在干燥的路面上,某种汽车的刹车距离s (m)与车速v (km/h)之间的关系如下表:
1
v (km/h) … 40 60 80 100 120 …
s (m) … 2 4.2 7.2 11 15.6 …
典题精讲
(1)在平面直角坐标系中描出每对(v,s)所对应的点,并用平滑的曲线顺次连接各点.
解:(1)如图.
典题精讲
(2)利用图像验证刹车距离众s(m)与车速v(km/h)是否具有
如下关系:
解:分别令v=40 km/h,60 km/h,80 km/h,100 km/h,
120 km/h,由
分别可得s=2 m,4.2 m,7.2 m,11 m,15.6 m.
∴刹车距离s (m)与车速v (km/h)
具有 的关系.
典题精讲
(3)求s=9 m时的车速v.
解:令s=9 m,则
解得v1=-100(km/h)(舍去),v2=90(km/h).
∴当s=9 m时,车速v=90 km/h.
典题精讲
某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a 元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t (t 为正整数)的增大而增大,a 的取值范围应为_____________.
2
0<a<6
探索新知
2
知识点
利用二次函数的最值解实际问题
利用二次函数解决实际生活中的利润问题,一般运用“总利润=每件商品所获利润×销售件数”或“总利润=总售价-总成本”建立利润与销售单价之间的二次函数关系式,求其图象的顶点坐标,获取最值.
探索新知
例2 某旅馆有客房120间,每间房的日租金为160元时,每天都客满.
经市场调查发现,如果每间客房的日租金增加10元,那么客房每
天出租数会减少6间.不考虑其他因素,旅馆将每间客房的日租金
提高到多少元时,客房日租金的总收入最高?最高总收入是多少?
探索新知
设每间客房的日租金提高10x 元,则每天客房出租数会
减少6x 间.设客房日租金总收入为 y 元,
则 y = (160+10x ) (120-6x )= -60 (x-2)2+ 19 440.
∵x ≥0,且120-6x >0,∴0≤x< 20.
当x =2时,y最大= 19 440.
这时每间客房的日租金为160 +10×2=180 (元).
因此,每间客房的日租金提高到180元时,客房总收人
最高,最高收入为 19 440 元.
解:
探索新知
例3 一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量
为2万件.今年计划通过适当增加成本来提高产品的档次,以拓展市场,若今
年这种玩具每件的成本比去年每件的成本增加0.7x 倍,今年这种玩具每件的出
厂价比去年每件的出厂价相应提高0.5x 倍,则预计今年年销售量将比去年年销
售量增加x 倍(0<x≤1).
(1)用含x 的代数式表示:今年生产的这种玩具每件的成本为___元,今年生产的
这种玩具每件的出厂价为____元;
(2)求今年这种玩具每件的利润y (元)与x 之间的函数关系式;
(3)设今年这种玩具的年销售利润为W 万元,求当x 为何值时,今年的年销售利
润最大,最大年销售利润是多少万元?
探索新知
由题意知今年这种玩具每件的成本是去年的(1+0.7x )倍,每件的
出厂价是去年每件的出厂价的 (1+0.5x )倍,今年的年销售量是去
年年销售量的 (1+x )倍.
解:(1)(10+7x );(12+6x )
(2)y=(12+6x )-(10+7x )=2-x,
即y 与x 的函数关系式为 y=2-x.
(3)W=2(1+x )(2-x )=-2x 2+2x+4=-2(x-5)2+4.5,
∵0<x≤1,∴当x=0.5时,W 有最大值.
W最大值=4.5.
答:当x=0.5时,今年的年销售利润最大,最大年销
售利润为4.5万元.
导引:
探索新知
总 结
本题利用建模思想求解,由今年与去年这种玩具的成本价、出厂价、销售量的倍数关系可以得到今年这种玩具的成本价、出厂价、销售量的表达式,再由“总利润=每件商品所获利润×销售件数”可得二次函数的表达式,进而求出其最大值.
典题精讲
1 某旅行社在五一期间接团去外地旅游,经计算,收益y (元)与旅行团人数x (人)满足表达式y=-x 2+100x+28 400,要使收益最大,则此旅行团应有( )
A.30人 B.40人
C.50人 D.55人
C
典题精讲
某网店销售某款童装,每件售价60元,每星期可卖300件,为了
促销,该网店决定降价销售.市场调查反映:每降价1元,每星期
可多卖30件.已知该款童装每件成本价40元,设该款童装每件售
价x 元,每星期的销售量为y 件.
(1)求y 与x 之间的函数表达式.
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润
是多少元?
(3)若该网店每星期想要获得不低于6 480元的利润,每星期至少
要销售该款童装多少件?
典题精讲
(1) y=300+30(60-x )=-30x+2 100.
(2)设每星期的销售利润为W 元,
则W=(x-40)(-30x+2 100)
=-30(x-55)2+6 750.
∴当x=55时,W 取最大值为6 750.
∴每件售价定为55元时,每星期的销售利润最大,
最大利润为6 750元.
解:
典题精讲
(3)由题意得(x-40)(-30x+2 100)≥6 480,
解得52≤x≤58.
当x=52时,销售量为300+30×8=540(件),
当x=58时,销售量为300+30×2=360(件),
∴该网店每星期想要获得不低于6 480元的利润,
每星期至少要销售该款童装360件.
易错提醒
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y (kg)与销售单价x (元)符合一次函数关系,如图是 y 与x 的函数关系图象.
易错提醒
(1)求 y 与x 的函数表达式;
(2)设该水果销售店试销草莓获得的利润为W 元,求W 的最大值.
易错点:将销售额当销售利润而致错
易错提醒
(1)设y 与x 的函数表达式为 y=kx+b,
根据题意,得
解得
∴y 与x 的函数表达式为 y=-2x+340(20≤x≤40).
解:
k=-2,
b=340.
20k+b=300,
30k+b=280.
易错提醒
(2)由已知得W=(x-20)(-2x+340)
=-2x 2+380x-6 800
=-2(x-95)2+11 250,
∵-2<0,
∴当x≤95时,W 随x 的增大而增大.
∵20≤x≤40,
∴当x=40时,W 最大,
最大值为-2×(40-95)2+11 250=5 200.
学以致用
小试牛刀
1 在一幅长60 cm,宽40 cm的矩形油画的四周镶一条金色
纸边,制成一幅矩形挂图,如图所示,如果要使整幅挂图
的面积是 y cm2,设金色纸边的宽度为x cm,那么 y 关
于x 的函数表达式是( )
A.y=(60+2x )(40+2x )
B.y=(60+x )(40+x )
C.y=(60+2x )(40+x )
D.y=(60+x )(40+2x )
A
2 心理学家发现:学生对概念的接受能力y 与提出概念的时间
x (min)之间是二次函数关系,当提出概念13min时,学生对
概念的接受能力最大,为59.9;当提出概念30 min时,学生
对概念的接受能力就剩下31,则 y 与x 满足的二次函数表达
式为( )
A.y=-(x-13)2+59.9
B.y=-0.1x 2+2.6x+31
C.y=0.1x 2-2.6x+76.8
D.y=-0.1x 2+2.6x+43
D
小试牛刀
小试牛刀
随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的
选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,
C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点
与文化宫距离为x (单位:km),乘坐地铁的时间y1(单位:min)是关于
x 的一次函数,其关系如下表:
地铁站 A B C D E
x/km 8 9 10 11.5 13
y1/min 18 20 22 25 28
小试牛刀
解:
(1)求y1关于x 的函数表达式;
(2)李华骑单车的时间(单位:min)也受x 的影响,其关系
可用y2= x 2-11x+78来描述,请问:李华应选择在
哪一站出地铁,才能使他从文化宫回到家所需的时间
最短?并求出最短时间.
(1)设y1=kx+b,将(8,18),(9,20)的坐标代入,
得 解得
故y1关于x 的函数表达式为y1=2x+2.
小试牛刀
(2)设李华从文化宫回到家所需的时间为y (单位:min),
则 y=y1+y2=2x+2+ x 2-11x+78= x 2-9x+80,
∴当x=9时,y 有最小值,ymin= =39.5.
答:李华应选择在B 站出地铁,才能使他从文化宫回到家所需的时
间最短,最短时间为39.5 min.
小试牛刀
某水果店在两周内,将标价为10元/斤的某种水果,经过两次降
价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x 天(x 为整数)的售价、销量及
储存和损耗费用的相关信息如下表所示.已知该种水果的进价
为4.1元/斤,设销售该水果第x 天的利润为y 元,求y 与x
(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
小试牛刀
时间x/天 1≤x<9 9≤x<15 x≥15
售价/(元/斤) 第1次降价
后的价格 第2次降价
后的价格
销量/斤 80-3x 120-x
储存和损耗
费用/元 40+3x 3x 2-64x+400
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
小试牛刀
(1)设该种水果每次降价的百分率是x,
由题意得10(1-x )2=8.1,
解得x=10%或x=190%(舍去).
答:该种水果每次降价的百分率是10%.
(2)当1≤x<9时,第一次降价后的价格为10×(1-10%)=9(元/斤),
∴y=(9-4.1)(80-3x )-(40+3x )=-17.7x+352.
∵-17.7<0,∴y 随x 的增大而减小,
∴当x=1时,y 有最大值,
y最大值=-17.7×1+352=334.3.
当9≤x<15时,第2次降价后的价格为8.1元/斤,
解:
小试牛刀
∴y=(8.1-4.1)(120-x )-(3x 2-64x+400)
=-3x 2+60x+80=-3(x-10)2+380,
∵-3<0,∴当9≤x≤10时,y 随x 的增大而增大,
当10<x<15时,y 随x 的增大而减小.
∴当x=10时,y 有最大值,y最大值=380.
∵334.3<380,∴当x=10时,y 取最大值.
综上所述,y 与x (1≤x< 15)之间的函数关系式为
y= 第10天时销售利润最大.
(3)设第15天在第14天的价格基础上降a 元,
由题意得380-127.5≤(4-a)×(120-15)-(3×152-64×
15+400),解得a ≤0.5.
答:第15天在第14天的价格基础上最多可降0.5元.
小试牛刀
5 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x 天(1≤x≤90,且x 为整数)的售价与销售量的相关信息如图和下表所示.已知商品的进价为30元/件,设该商品的售价为y (单位:元/件),每天的销售量为p (单位:件),每天的销售利润为w (单位:元).
(1)求出w 与x 的函数表达式.
(2)问销售该商品第几天时,当天的销售
利润最大?并求出最大利润.
(3)该商品在销售过程中,共有多少天每
天的销售利润不低于5 600元?请直接写出结果.
时间x/天 1 30 60 90
每天的销售量p/件 198 140 80 20
小试牛刀
解:
(1)当1≤x≤50时,设商品的售价y 与时间x 的函数表达式为y
=kx+b (k,b 为常数,且k≠0),
根据题意,得
∴ 解得
∴当1≤x≤50时,售价y 与时间x 的函数表达式为y=x+40.
当50<x≤90时,y=90.
∴售价y 与时间x 的函数表达式为
y=
由表格可知,每天的销售量p 与时间x 成一次函数.
小试牛刀
设每天的销售量p 与时间x 的函数表达式为p=mx+n (m,n 为常数,且m≠0),
根据题意,得
∴ 解得
∴p=-2x+200(1≤x≤90,且x 为整数).
当1≤x≤50时,w=(y-30)·p=(x+40-30)(-2x+200)=
-2x 2+180x+2 000;
当50<x≤90时,w=(90-30)·(-2x+200)=-120x+12 000.
综上,每天的销售利润w 与时间x 的函数表达式是
w=
小试牛刀
(2)当1≤x≤50时,
w=-2x 2+180x+2 000=-2(x-45)2+6 050,
∵a=-2<0且1≤x≤50,
∴当x=45时,w 取最大值,最大值为6 050.
当50<x≤90时,w=-120x+12 000,
∵-120<0,
∴w 随x 的增大而减小.∴w<6 000.
综上可知,当x=45时,w 最大,最大值为6 050.
即销售该商品第45天时,当天的销售利润最大,最大
利润是6 050元.
(3)24天.
课堂小结
课堂小结
利润问题的基本关系式:
总利润=单件利润×销售总量.
若销售单价每提高m 元,销售量相应减少n 件,
设提高x 元,则现销售量=原销售量-
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
