【班海精品】冀教版(新)九下-30.5 二次函数与一元二次方程的关系 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-30.5 二次函数与一元二次方程的关系 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
30.5 二次函数与一元二次方程的关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
一次函数 y=kx+b 的图象与x 轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数 y=kx+b 的图象与x 轴的交点的横坐标就是一元一次方程 kx+b=0的根 .
温故知新
新课精讲
探索新知
1
知识点
利用二次函数的图像解一元二次方程
利用二次函数的图像求一元二次方程的近似根的一般步骤:
(1)画出二次函数 y=ax 2+bx+c 的图像;
(2)确定二次函数的图像与x 轴交点的个数,看交点的横坐
标在哪两个整数之间;
探索新知
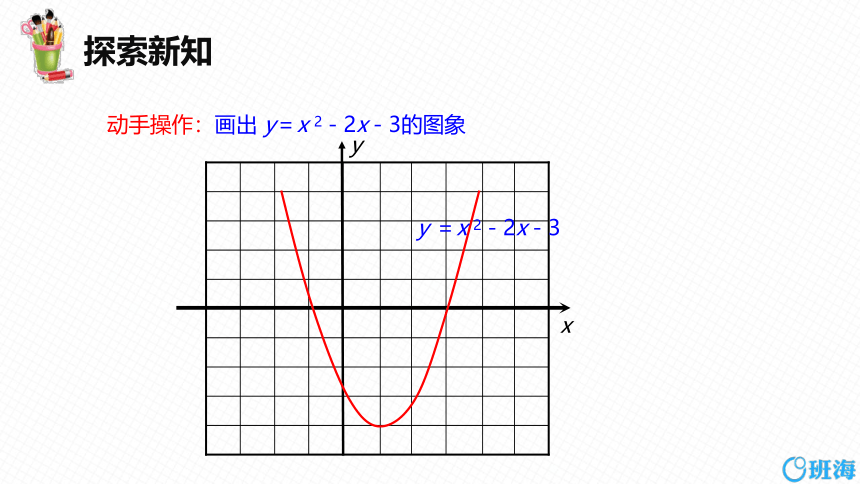
动手操作:画出 y=x 2-2x-3的图象
x
y
y =x 2-2x-3
探索新知
探究:图像与 x 轴的交点坐标是什么?
函数 y=x 2-2x-3的图像与x 轴两个交点为(-1,0)(3,0)
方程x 2-2x-3 =0的两根是 x1= -1,x2 = 3
你发现了什么?
(1)二次函数 y=ax 2+bx+c 与x 轴的交点的横坐标就是
当y=0时一元二次方程ax 2+bx+c=0的根
(2)二次函数的交点问题可以转化为一元二次方程去解决.
探索新知
解:如图 ,画出二次函数
y=x 2-2x-6 的图像.
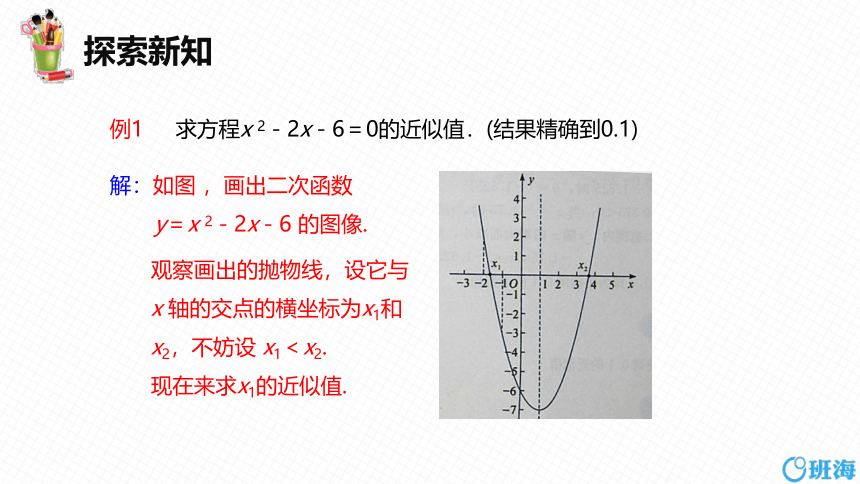
例1 求方程x 2-2x-6=0的近似值.(结果精确到0.1)
观察画出的抛物线,设它与x 轴的交点的横坐标为x1和x2,不妨设 x1<x2.
现在来求x1的近似值.
探索新知
容易看出:当 x=-2 时,y>0;
当x=-1时,y<0,且在-2<x<-1范围内,
y 随x 的增大二减小,所以-2<x1<-1
(2)取-2和-1的中间数-1.5(中间数为 ),
代入表达式中试值
当 x=-1.5时,y =(-1.5)2-2×(-1.5)-6 =-0.75<0;
当x=-2 时,y>0;
在-2<x<-1.5范围内,y 随x 的增大而减小,
所以-2<x1<-1.5
探索新知
(3)取-2和-1.5的中间数-1.75,代入表达式中试值.
当 x=-1.75时,y =(-1.75)2-2×(-1.75)-6
=0.5625>0;
当x=-1.5 时,y<0.
在-1.75<x<-1.5范围内,y 随x 的增大而减小,
所以-1.75<x1<-1.5.
探索新知
(4)取-1.75和-1.5的中间数-1.625,代入表达式中试值.
当 x=-1.625时,y=(-1.625)2-2×(-1.625)-6
=-0.109375<0;
当x=-1.75 时,y>0.
在-1.75<x<-1.625范围内,y 随x 的增大而减小,
所以-1.75<x1<-1.625.
x1≈-1.7即为精确到0.1的近似值.
探索新知
解:先把方程化成x 2=-2x+3.
如图,在同一直角坐标系中
分别画出函数y=x 2和
y=-2x+3的图像,得到它
们的交点为(-3,9)和(1,1),
则方程x 2+2x-3=0的解为x=-3或x=1.
例2 利用函数的图像,求方程x 2+2x-3=0的根.
探索新知
总 结
利用图像交点法求一元二次方程的根的步骤:
(1)将ax 2+bx+c=0化为ax 2=-bx-c 的形式;
(2)在同一坐标系中画出 y=ax 2与 y=-bx-c 的图像;
(3)观察图像:两图像的公共点情况即为方程的根的情况,
如有公共点,则公共点的横坐标即为ax 2+bx+c=0的根.
1 求例题中x2精确到0.1的近似值.
解:如图 ,画出二次函数
y =x 2-2x-6的图像.
观察画出的抛物线,现在求 x2
的近似值.
(1)容易看出:当x=3时,y<0,当x=4时,y>0,且在3<x<4范围内,y 随x 的增大而增大,∴3<x2<4.
典题精讲
(2)取3和4的中间数3.5代入表达式中试值.
当x=3.5时,y=3.52-2×3.5-6=-0.75<0;
当x=4时,y>0,在3.5<x<4范围内,
y 随x 的增大而增大, ∴3.5<x2<4.
(3)取3.5和4的中间数3.75代入表达式中试值.
当x=3.75时,y=3.752-2×3.75-6=0.562 5>0;
当x=3.5时,y<0. 在3.5<x<3.75范围内,
y 随x 的增大而增大,
∴3.5<x2<3.75.
典题精讲
(4)取3.5和3.75的中间数3.625代入表达式中试值.
当x=3.625时,
y=3.6252-2×3.625-6=-0.109 375<0;
当x=3.75时,y>0.在3.625<x<3.75范围内,
y 随x 的增大而增大,∴3.625<x2<3.75.
∴可取x2≈3.7为精确到0.1的近似值.
典题精讲
典题精讲
2 二次函数 y=ax 2+bx+c 的图像如图所示,则一元二
次方程ax 2+bx+c=0的两根为( )
A.x1=1,x2=-3
B.x1=x2=-1
C.x1=x2=3
D.x1=-1,x2=3
D
典题精讲
3 如图是二次函数 y=ax 2+bx+c 的图像,图像上有两点
分别为A (2.18,-0.61),B (2.68,0.44),则方程ax 2+
bx+c=0的一个解只可能是( )
A.2.18
B.2.68
C.-0.51
D.2.55
D
典题精讲
下表是一组二次函数 y=x 2+3x-5的自变量x 与函数值y 的对应值:
4
那么方程x 2+3x-5=0的一个近似根是( )
A.1 B.1.1 C.1.2 D.1.3
x 1 1.1 1.2 1.3 1.4
y -1 -0.49 0.04 0.59 1.16
C
典题精讲
(2)解法二:利用二次函数图像与x 轴的交点求解.如
图①,把方程x 2-x-1=0的解看成是二次函数 y
=_____________的图像与x
轴交点的横坐标x1,x2,
则x1,x2就是方程的解.
x 2-x-1
(3)解法三:利用两个函数图像的交点求解.
①把方程x 2-x-1=0的解看成是二次函数y=
________的图像与直线
y=_______的交点的横坐标;
②在图②中画出这两个函数
的图像,用x1,x2在x 轴上
标出方程的解.
x 2-x
1
②略.
解:
典题精讲
探索新知
2
知识点
利用二次函数的图像解一元二次不等式
根据图像可直观地回答使得y 的值大于、等于或小
于零时x 的取值(范围),具体如下表所述:
图像 函数值 自变量的取值(范围)
y>0 x<x1或x>x2
y=0 x=x1或x=x2
y<0 x1<x<x2
y>0 x1<x<x2
y=0 x=x1或x=x2
y<0 x<x1或x>x2
探索新知
例3 画出抛物线 y=-x 2+4x+5,观察抛物线,回答下
列问题:
(1)x 为何值时,函数值 y>0
(2)x 为何值时,函数值 y=0
(3)x 为何值时,函数值 y<0
导引:根据抛物线的简易画法,先确定顶点以及抛物线与x
轴和y 轴的交点,当函数值 y>0时,对应图像上的点
在x 轴上方;当函数值 y=0时,对应图像上的点位于
x 轴上;当函数值 y<0时,对应图像上的点在x 轴的
下方.
探索新知
解:∵y=-x 2+4x+5=-(x 2-4x)+5=-(x 2-4x+4)+9=
-(x-2)2+9. ∴抛物线的顶点坐标
为(2,9),对称轴为直线x=2.
令-x 2+4x+5=0,即x 2-4x-5=
0,∴x1=5,x2=-1.∴抛物线与x
轴的两个交点为(-1,0),(5,0).
令x=0,则y=5,即抛物线与y 轴的
交点为(0,5).由抛物线的对称性知抛物线上的另一点为
(4,5).在坐标系中描出各点,并连线得到如图所示的图
象.观察图像会发现:(1)当-1<x<5时,函数值y>0;
(2)当x=-1或x=5时,函数值 y=0;
(3)当x<-1或x>5时,函数值 y<0
探索新知
总 结
(1)作抛物线 y=ax 2+bx+c (b 2-4ac>0)一般采用“五点法”,
而这“五点”一般为抛物线顶点,与x 轴的两交点,与y 轴的
交点及它关于对称轴的对称点.
(2)根据二次函数值的取值范围确定自变量的取值范围,一般要画出
二次函数的图像,观察图像解答,抛物线在 x 轴上方的部分,对
应的函数值大于0;抛物线在x 轴下方的部分,对应的函数值小于
0;抛物线与x 轴的公共点,对应的函数值等于0.
探索新知
例4 抛物线 y=ax 2+bx+c (a≠0)的对称轴为直线x=-1,与x 轴
的一个交点A 在(-3,0)和(-2,0)之间,其部分图像如图所
示,则下列结论:①4ac-b 2<0;②2a-b=0;③a+b+c
<0;④点M (x1,y1),N (x2,y2)在抛物线上,若x1<x2,则y1
<y2.正确结论的个数是( )
A.1 B.2
C.3 D.4
C
探索新知
导引:观察图像可知二次函数对应的一元二次方程有两个不相等的实数解,所以Δ=b 2-4ac >0,即4ac-b 2<0,故①正确;因为抛物线的对称轴为直线x=-1,所以- =-1,即b=2a,2a-b=0,故②正确;由二次函数图像的对称性可知抛物线与x 轴的另一个交点位于(0,0)和(1,0)之间,所以当x=1时,y<0,即a+b+c<0,故③正确;由于二次函数在对称轴两侧的增减性不一样,当x1y2;当x1<-1<x2且-1-x1=x2-(-1)时,y1=y2,所以④错误.所以此题正确的结论有3个.故选C.
典题精讲
如图,直线 y=mx+n 与抛物线 y=ax 2+bx+c 交于A (-1,p ),B (4,q )两点,则关于x 的不等式mx+n>ax 2+bx+c 的解集是_______________.
1
x<-1或x>4
典题精讲
如图,已知顶点为(-3,-6)的抛物线 y=ax 2+bx+c 经过点(-1,-4),则下列结论中错误的是( )
A.b 2>4ac
B.ax 2+bx+c ≥-6
C.若点(-2,m ),(-5,n )
在抛物线上,则m>n
D.关于x 的一元二次方程ax 2+bx+c=-4
的两根为-5和-1
2
C
易错提醒
用图像法求x 2-x+ =0的解.
易错点:不考虑方程根的情况盲目作图像而致错
画出抛物线 y =x 2-x+ (如图).
由图像可知抛物线与x 轴的交点为( ,0),
所以原方程的解为x1=x2=
解:
学以致用
小试牛刀
已知一次函数y1=4x,二次函数 y2=2x 2+2,在实数范围内,对于x 的同一个值,这两个函数所对应的函数值分别为y1与y2,则下列关系正确的是( )
A.y1>y2 B.y1≥y2
C.y1<y2 D.y1≤y2
1
D
小试牛刀
小明在复习数学知识时,针对“求一元二次方程的解”总结了以下几种方法,请你将有关内容补充完整.
例题:求一元二次方程 x 2-x-1=0的两个解.
(1)解法一:选择一种合适的方法(公式法、配方法、因式分解法)求解.
2
(1)公式法:
∵a=1,b=-1,c=-1,
∴Δ=b 2-4ac=(-1)2-4×1×(-1)=5>0.
∴
即x1= x2= .
解:
小试牛刀
二次函数 y=ax 2+bx+c (a≠0)的图像如图所示,根据
图像解答下列问题:
(1)写出方程ax 2+bx+c=0的两个根;
(2)写出不等式ax 2+bx+c >0的解集;
(3)写出 y 随 x 的增大而减小的自变量x 的取值范围;
(4)若方程ax 2+bx+c=k 有两个不相等的实数根,
求k 的取值范围.
小试牛刀
(1)x1=1,x2=3.
(2)1<x<3.
(3)x ≥2.
(4)∵方程ax 2+bx+c=k 有两个不相等的实数根,
∴抛物线 y=ax 2+bx+c-k 与x 轴有两个交点,即抛
物线 y=ax 2+bx+c 向下平移k 个单位长度后与 x 轴有
两个交点.
由图像可知抛物线 y=ax 2+bx+c 向下平移2个单位长
度后与x 轴有一个公共点,∴k<2.
解:
小试牛刀
4 根据下列要求,解答相关问题.
(1)请补全以下求不等式-2x 2-4x ≥0的解集的过程.
①构造函数,画出图像:根据不等式特征构造二次函数 y=-2x 2-4x,并在下面的坐标系中(如图①)画出二次函数 y=-2x 2-4x 的图像(只画出图像即可).
②求得界点,标示所需:当 y=0时,求得方程-2x 2-4x=0的解为____________,并用锯齿线标示出函数 y=-2x 2-4x 的图像中y ≥0的部分;
③借助图像,写出解集:由所标示图像,可得不等式-2x 2-4x ≥0的解集为__________________.
小试牛刀
(2)利用(1)中求不等式解集的步骤,求不等式x 2-2x+1<4的解集.
①构造函数,在图②中画出图像;
②求得界点,标示所需;
③借助图像,写出解集.
(3)参照以上两个求不等式解集的过程,借助一元二次方
程的求根公式,直接写出关
于x 的不等式ax 2+bx+c>0
(a>0)的解集.
小试牛刀
(1)①图略.②x1=0,x2=-2;图略.③-2≤x≤0
(2)①构造二次函数 y=x 2-2x+1,并画出图像(图略).
②当 y=4时,求得方程x 2-2x+1=4的解为x1=3,
x2=-1;图略.
③借助图像,直接写出不等式x 2-2x+1<4的解集:
-1<x<3.
(3)①当b 2-4ac>0时,解集为x> 或x<
;②当b 2-4ac=0时,解集为x≠
- ;
③当b 2-4ac<0时,解集为全体实数.
解:
小试牛刀
5 已知二次函数 y=ax 2+bx+c (a>0)的图像与x 轴交于
A (x1,0),B (x2,0)(x1<x2)两点,与y 轴交于点C,x1,
x2是方程x 2+4x-5=0的两根.
(1)若抛物线的顶点为D,求S△ABC ∶S△ACD;
(2)若∠ADC=90°,求二次函数的表达式.
解:
(1)解方程x 2+4x-5=0,得x1=-5,x2=1. ∴A点的坐标为
(-5,0),B 点的坐标为(1,0),则抛物线为 y=a (x+5)
(x-1)=ax 2+4ax-5a,可得D 点的坐标为(-2,-9a),
C 点的坐标为(0,-5a).依题意画出图形,如图所示,则
OA=5,OB=1,AB=6,OC=5a,过点D 作 DE⊥y 轴
于点E,则DE=2,OE=9a,CE=OE-OC=4a.
小试牛刀
∴S△ACD=S梯形ADEO-S△CDE-S△AOC=
(DE+OA)·OE- DE · CE- OA·OC=
×(2+5)×9a- ×2×4a- ×5×5a=15a,
S△ABC= ×6×5a=15a,∴S△ABC∶S△ACD=1∶1.
(2)∵∠ADC=90°,∴AC 2=AD 2+CD 2.即52+(5a)2=(5-
2)2+(9a)2+22+(9a-5a)2,即72a 2=12.则a=± .
∵a>0,∴a= .故二次函数的表达式为 y= (x+5)
(x-1),即 y= x 2+ x- .
课堂小结
课堂小结
利用图像求一元二次方程的根的方法:直接画出二次函数y=ax 2+bx+c 的图像,则图像与x 轴交点的横坐标就是一元二次方程ax 2+bx+c=0的根.其步骤一般为:
(1)作出二次函数 y=ax 2+bx+c 的图像;
(2)观察图像与x 轴交点的个数;
(3)若图像与x 轴有交点,估计出图像与x 轴交点的横坐标
即可得到一元二次方程的近似根.
课堂小结
图像 函数值 自变量的取值(范围)
y>0 x<x1或x>x2
y=0 x=x1或x=x2
y<0 x1<x<x2
y>0 x1<x<x2
y=0 x=x1或x=x2
y<0 x<x1或x>x2
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
30.5 二次函数与一元二次方程的关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
一次函数 y=kx+b 的图象与x 轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数 y=kx+b 的图象与x 轴的交点的横坐标就是一元一次方程 kx+b=0的根 .
温故知新
新课精讲
探索新知
1
知识点
利用二次函数的图像解一元二次方程
利用二次函数的图像求一元二次方程的近似根的一般步骤:
(1)画出二次函数 y=ax 2+bx+c 的图像;
(2)确定二次函数的图像与x 轴交点的个数,看交点的横坐
标在哪两个整数之间;
探索新知
动手操作:画出 y=x 2-2x-3的图象
x
y
y =x 2-2x-3
探索新知
探究:图像与 x 轴的交点坐标是什么?
函数 y=x 2-2x-3的图像与x 轴两个交点为(-1,0)(3,0)
方程x 2-2x-3 =0的两根是 x1= -1,x2 = 3
你发现了什么?
(1)二次函数 y=ax 2+bx+c 与x 轴的交点的横坐标就是
当y=0时一元二次方程ax 2+bx+c=0的根
(2)二次函数的交点问题可以转化为一元二次方程去解决.
探索新知
解:如图 ,画出二次函数
y=x 2-2x-6 的图像.
例1 求方程x 2-2x-6=0的近似值.(结果精确到0.1)
观察画出的抛物线,设它与x 轴的交点的横坐标为x1和x2,不妨设 x1<x2.
现在来求x1的近似值.
探索新知
容易看出:当 x=-2 时,y>0;
当x=-1时,y<0,且在-2<x<-1范围内,
y 随x 的增大二减小,所以-2<x1<-1
(2)取-2和-1的中间数-1.5(中间数为 ),
代入表达式中试值
当 x=-1.5时,y =(-1.5)2-2×(-1.5)-6 =-0.75<0;
当x=-2 时,y>0;
在-2<x<-1.5范围内,y 随x 的增大而减小,
所以-2<x1<-1.5
探索新知
(3)取-2和-1.5的中间数-1.75,代入表达式中试值.
当 x=-1.75时,y =(-1.75)2-2×(-1.75)-6
=0.5625>0;
当x=-1.5 时,y<0.
在-1.75<x<-1.5范围内,y 随x 的增大而减小,
所以-1.75<x1<-1.5.
探索新知
(4)取-1.75和-1.5的中间数-1.625,代入表达式中试值.
当 x=-1.625时,y=(-1.625)2-2×(-1.625)-6
=-0.109375<0;
当x=-1.75 时,y>0.
在-1.75<x<-1.625范围内,y 随x 的增大而减小,
所以-1.75<x1<-1.625.
x1≈-1.7即为精确到0.1的近似值.
探索新知
解:先把方程化成x 2=-2x+3.
如图,在同一直角坐标系中
分别画出函数y=x 2和
y=-2x+3的图像,得到它
们的交点为(-3,9)和(1,1),
则方程x 2+2x-3=0的解为x=-3或x=1.
例2 利用函数的图像,求方程x 2+2x-3=0的根.
探索新知
总 结
利用图像交点法求一元二次方程的根的步骤:
(1)将ax 2+bx+c=0化为ax 2=-bx-c 的形式;
(2)在同一坐标系中画出 y=ax 2与 y=-bx-c 的图像;
(3)观察图像:两图像的公共点情况即为方程的根的情况,
如有公共点,则公共点的横坐标即为ax 2+bx+c=0的根.
1 求例题中x2精确到0.1的近似值.
解:如图 ,画出二次函数
y =x 2-2x-6的图像.
观察画出的抛物线,现在求 x2
的近似值.
(1)容易看出:当x=3时,y<0,当x=4时,y>0,且在3<x<4范围内,y 随x 的增大而增大,∴3<x2<4.
典题精讲
(2)取3和4的中间数3.5代入表达式中试值.
当x=3.5时,y=3.52-2×3.5-6=-0.75<0;
当x=4时,y>0,在3.5<x<4范围内,
y 随x 的增大而增大, ∴3.5<x2<4.
(3)取3.5和4的中间数3.75代入表达式中试值.
当x=3.75时,y=3.752-2×3.75-6=0.562 5>0;
当x=3.5时,y<0. 在3.5<x<3.75范围内,
y 随x 的增大而增大,
∴3.5<x2<3.75.
典题精讲
(4)取3.5和3.75的中间数3.625代入表达式中试值.
当x=3.625时,
y=3.6252-2×3.625-6=-0.109 375<0;
当x=3.75时,y>0.在3.625<x<3.75范围内,
y 随x 的增大而增大,∴3.625<x2<3.75.
∴可取x2≈3.7为精确到0.1的近似值.
典题精讲
典题精讲
2 二次函数 y=ax 2+bx+c 的图像如图所示,则一元二
次方程ax 2+bx+c=0的两根为( )
A.x1=1,x2=-3
B.x1=x2=-1
C.x1=x2=3
D.x1=-1,x2=3
D
典题精讲
3 如图是二次函数 y=ax 2+bx+c 的图像,图像上有两点
分别为A (2.18,-0.61),B (2.68,0.44),则方程ax 2+
bx+c=0的一个解只可能是( )
A.2.18
B.2.68
C.-0.51
D.2.55
D
典题精讲
下表是一组二次函数 y=x 2+3x-5的自变量x 与函数值y 的对应值:
4
那么方程x 2+3x-5=0的一个近似根是( )
A.1 B.1.1 C.1.2 D.1.3
x 1 1.1 1.2 1.3 1.4
y -1 -0.49 0.04 0.59 1.16
C
典题精讲
(2)解法二:利用二次函数图像与x 轴的交点求解.如
图①,把方程x 2-x-1=0的解看成是二次函数 y
=_____________的图像与x
轴交点的横坐标x1,x2,
则x1,x2就是方程的解.
x 2-x-1
(3)解法三:利用两个函数图像的交点求解.
①把方程x 2-x-1=0的解看成是二次函数y=
________的图像与直线
y=_______的交点的横坐标;
②在图②中画出这两个函数
的图像,用x1,x2在x 轴上
标出方程的解.
x 2-x
1
②略.
解:
典题精讲
探索新知
2
知识点
利用二次函数的图像解一元二次不等式
根据图像可直观地回答使得y 的值大于、等于或小
于零时x 的取值(范围),具体如下表所述:
图像 函数值 自变量的取值(范围)
y>0 x<x1或x>x2
y=0 x=x1或x=x2
y<0 x1<x<x2
y>0 x1<x<x2
y=0 x=x1或x=x2
y<0 x<x1或x>x2
探索新知
例3 画出抛物线 y=-x 2+4x+5,观察抛物线,回答下
列问题:
(1)x 为何值时,函数值 y>0
(2)x 为何值时,函数值 y=0
(3)x 为何值时,函数值 y<0
导引:根据抛物线的简易画法,先确定顶点以及抛物线与x
轴和y 轴的交点,当函数值 y>0时,对应图像上的点
在x 轴上方;当函数值 y=0时,对应图像上的点位于
x 轴上;当函数值 y<0时,对应图像上的点在x 轴的
下方.
探索新知
解:∵y=-x 2+4x+5=-(x 2-4x)+5=-(x 2-4x+4)+9=
-(x-2)2+9. ∴抛物线的顶点坐标
为(2,9),对称轴为直线x=2.
令-x 2+4x+5=0,即x 2-4x-5=
0,∴x1=5,x2=-1.∴抛物线与x
轴的两个交点为(-1,0),(5,0).
令x=0,则y=5,即抛物线与y 轴的
交点为(0,5).由抛物线的对称性知抛物线上的另一点为
(4,5).在坐标系中描出各点,并连线得到如图所示的图
象.观察图像会发现:(1)当-1<x<5时,函数值y>0;
(2)当x=-1或x=5时,函数值 y=0;
(3)当x<-1或x>5时,函数值 y<0
探索新知
总 结
(1)作抛物线 y=ax 2+bx+c (b 2-4ac>0)一般采用“五点法”,
而这“五点”一般为抛物线顶点,与x 轴的两交点,与y 轴的
交点及它关于对称轴的对称点.
(2)根据二次函数值的取值范围确定自变量的取值范围,一般要画出
二次函数的图像,观察图像解答,抛物线在 x 轴上方的部分,对
应的函数值大于0;抛物线在x 轴下方的部分,对应的函数值小于
0;抛物线与x 轴的公共点,对应的函数值等于0.
探索新知
例4 抛物线 y=ax 2+bx+c (a≠0)的对称轴为直线x=-1,与x 轴
的一个交点A 在(-3,0)和(-2,0)之间,其部分图像如图所
示,则下列结论:①4ac-b 2<0;②2a-b=0;③a+b+c
<0;④点M (x1,y1),N (x2,y2)在抛物线上,若x1<x2,则y1
<y2.正确结论的个数是( )
A.1 B.2
C.3 D.4
C
探索新知
导引:观察图像可知二次函数对应的一元二次方程有两个不相等的实数解,所以Δ=b 2-4ac >0,即4ac-b 2<0,故①正确;因为抛物线的对称轴为直线x=-1,所以- =-1,即b=2a,2a-b=0,故②正确;由二次函数图像的对称性可知抛物线与x 轴的另一个交点位于(0,0)和(1,0)之间,所以当x=1时,y<0,即a+b+c<0,故③正确;由于二次函数在对称轴两侧的增减性不一样,当x1
典题精讲
如图,直线 y=mx+n 与抛物线 y=ax 2+bx+c 交于A (-1,p ),B (4,q )两点,则关于x 的不等式mx+n>ax 2+bx+c 的解集是_______________.
1
x<-1或x>4
典题精讲
如图,已知顶点为(-3,-6)的抛物线 y=ax 2+bx+c 经过点(-1,-4),则下列结论中错误的是( )
A.b 2>4ac
B.ax 2+bx+c ≥-6
C.若点(-2,m ),(-5,n )
在抛物线上,则m>n
D.关于x 的一元二次方程ax 2+bx+c=-4
的两根为-5和-1
2
C
易错提醒
用图像法求x 2-x+ =0的解.
易错点:不考虑方程根的情况盲目作图像而致错
画出抛物线 y =x 2-x+ (如图).
由图像可知抛物线与x 轴的交点为( ,0),
所以原方程的解为x1=x2=
解:
学以致用
小试牛刀
已知一次函数y1=4x,二次函数 y2=2x 2+2,在实数范围内,对于x 的同一个值,这两个函数所对应的函数值分别为y1与y2,则下列关系正确的是( )
A.y1>y2 B.y1≥y2
C.y1<y2 D.y1≤y2
1
D
小试牛刀
小明在复习数学知识时,针对“求一元二次方程的解”总结了以下几种方法,请你将有关内容补充完整.
例题:求一元二次方程 x 2-x-1=0的两个解.
(1)解法一:选择一种合适的方法(公式法、配方法、因式分解法)求解.
2
(1)公式法:
∵a=1,b=-1,c=-1,
∴Δ=b 2-4ac=(-1)2-4×1×(-1)=5>0.
∴
即x1= x2= .
解:
小试牛刀
二次函数 y=ax 2+bx+c (a≠0)的图像如图所示,根据
图像解答下列问题:
(1)写出方程ax 2+bx+c=0的两个根;
(2)写出不等式ax 2+bx+c >0的解集;
(3)写出 y 随 x 的增大而减小的自变量x 的取值范围;
(4)若方程ax 2+bx+c=k 有两个不相等的实数根,
求k 的取值范围.
小试牛刀
(1)x1=1,x2=3.
(2)1<x<3.
(3)x ≥2.
(4)∵方程ax 2+bx+c=k 有两个不相等的实数根,
∴抛物线 y=ax 2+bx+c-k 与x 轴有两个交点,即抛
物线 y=ax 2+bx+c 向下平移k 个单位长度后与 x 轴有
两个交点.
由图像可知抛物线 y=ax 2+bx+c 向下平移2个单位长
度后与x 轴有一个公共点,∴k<2.
解:
小试牛刀
4 根据下列要求,解答相关问题.
(1)请补全以下求不等式-2x 2-4x ≥0的解集的过程.
①构造函数,画出图像:根据不等式特征构造二次函数 y=-2x 2-4x,并在下面的坐标系中(如图①)画出二次函数 y=-2x 2-4x 的图像(只画出图像即可).
②求得界点,标示所需:当 y=0时,求得方程-2x 2-4x=0的解为____________,并用锯齿线标示出函数 y=-2x 2-4x 的图像中y ≥0的部分;
③借助图像,写出解集:由所标示图像,可得不等式-2x 2-4x ≥0的解集为__________________.
小试牛刀
(2)利用(1)中求不等式解集的步骤,求不等式x 2-2x+1<4的解集.
①构造函数,在图②中画出图像;
②求得界点,标示所需;
③借助图像,写出解集.
(3)参照以上两个求不等式解集的过程,借助一元二次方
程的求根公式,直接写出关
于x 的不等式ax 2+bx+c>0
(a>0)的解集.
小试牛刀
(1)①图略.②x1=0,x2=-2;图略.③-2≤x≤0
(2)①构造二次函数 y=x 2-2x+1,并画出图像(图略).
②当 y=4时,求得方程x 2-2x+1=4的解为x1=3,
x2=-1;图略.
③借助图像,直接写出不等式x 2-2x+1<4的解集:
-1<x<3.
(3)①当b 2-4ac>0时,解集为x> 或x<
;②当b 2-4ac=0时,解集为x≠
- ;
③当b 2-4ac<0时,解集为全体实数.
解:
小试牛刀
5 已知二次函数 y=ax 2+bx+c (a>0)的图像与x 轴交于
A (x1,0),B (x2,0)(x1<x2)两点,与y 轴交于点C,x1,
x2是方程x 2+4x-5=0的两根.
(1)若抛物线的顶点为D,求S△ABC ∶S△ACD;
(2)若∠ADC=90°,求二次函数的表达式.
解:
(1)解方程x 2+4x-5=0,得x1=-5,x2=1. ∴A点的坐标为
(-5,0),B 点的坐标为(1,0),则抛物线为 y=a (x+5)
(x-1)=ax 2+4ax-5a,可得D 点的坐标为(-2,-9a),
C 点的坐标为(0,-5a).依题意画出图形,如图所示,则
OA=5,OB=1,AB=6,OC=5a,过点D 作 DE⊥y 轴
于点E,则DE=2,OE=9a,CE=OE-OC=4a.
小试牛刀
∴S△ACD=S梯形ADEO-S△CDE-S△AOC=
(DE+OA)·OE- DE · CE- OA·OC=
×(2+5)×9a- ×2×4a- ×5×5a=15a,
S△ABC= ×6×5a=15a,∴S△ABC∶S△ACD=1∶1.
(2)∵∠ADC=90°,∴AC 2=AD 2+CD 2.即52+(5a)2=(5-
2)2+(9a)2+22+(9a-5a)2,即72a 2=12.则a=± .
∵a>0,∴a= .故二次函数的表达式为 y= (x+5)
(x-1),即 y= x 2+ x- .
课堂小结
课堂小结
利用图像求一元二次方程的根的方法:直接画出二次函数y=ax 2+bx+c 的图像,则图像与x 轴交点的横坐标就是一元二次方程ax 2+bx+c=0的根.其步骤一般为:
(1)作出二次函数 y=ax 2+bx+c 的图像;
(2)观察图像与x 轴交点的个数;
(3)若图像与x 轴有交点,估计出图像与x 轴交点的横坐标
即可得到一元二次方程的近似根.
课堂小结
图像 函数值 自变量的取值(范围)
y>0 x<x1或x>x2
y=0 x=x1或x=x2
y<0 x1<x<x2
y>0 x1<x<x2
y=0 x=x1或x=x2
y<0 x<x1或x>x2
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
