【班海精品】冀教版(新)九下-31.2 随机事件的概率 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-31.2 随机事件的概率 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 09:33:47 | ||
图片预览











文档简介
(共37张PPT)
31.2 随机事件的概率
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于2的概率是多少
新课精讲
探索新知
1
知识点
用概率说明事件的合理性
用概率说明普通游戏是否公平,关键看获胜的概率是否相同,相同则公平,不相同则不公平.
探索新知
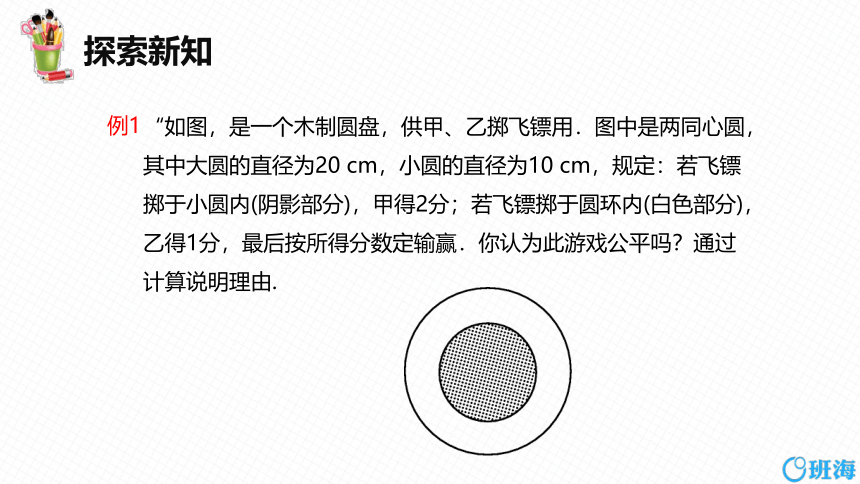
“如图,是一个木制圆盘,供甲、乙掷飞镖用.图中是两同心圆,其中大圆的直径为20 cm,小圆的直径为10 cm,规定:若飞镖掷于小圆内(阴影部分),甲得2分;若飞镖掷于圆环内(白色部分),乙得1分,最后按所得分数定输赢.你认为此游戏公平吗?通过计算说明理由.
例1
探索新知
游戏是否公平,关键要看游戏双方取胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.但要注意本题是按所得分数定输赢,而掷于小圆内甲的得分与掷于圆环内乙的得分不相等.
导引:
经计算可知,阴影部分的面积为78.5 cm2,白色部分的面积为235.5 cm2. 所以飞镖掷于圆环内的概率等于掷于小圆内的概率的3倍,而掷于小圆内甲的得分却是掷于圆环内乙的得分的2倍,所以这个游戏不公平.
解:
探索新知
总 结
判断游戏的公平性是通过概率来判断的,如果对于参加游戏的每一个人获胜的概率相等,则游戏公平,否则不公平.
典题精讲
1
甲、乙两人做掷硬币游戏. 掷一枚质地均匀的硬币,落地后,正而朝上,甲胜;反面朝上,乙胜.共掷了10次硬币,结果有6次正面朝上,4次反面朝上. 乙认为这个游戏不公平你同意他的看法吗?请说说你理由.
不同意.理由:因为掷一枚硬币出现正面朝上和反面朝上的概率均为 ,所以这个游戏是公平的.
解:
典题精讲
2
足球比赛前,裁判断通常要掷一枚硬币来决定比赛双方的场地与首先发球者,其主要原因是( )
A.让比赛更富有情趣
B.让比赛更具有神秘色彩
C.体现比赛的公平性
D.让比赛更有挑战性
C
典题精讲
3
甲乙两人玩一个游戏,判定这个游戏公平的标准是( )
A.游戏的规则由甲方确定
B.游戏的规则由乙方确定
C.游戏的规则由甲乙双方商定
D.游戏双方要各有50%赢的机会
D
典题精讲
4
同时抛掷两枚质地均匀的硬币,则下列事件发生的概率最大的是( )
A.两正面都朝上
B.两背面都朝上
C.一个正面朝上,另一个背面朝上
D.三种情况发生的概率一样大
C
典题精讲
5
一个箱子中装有红、黄、黑三个小球,这些球除颜色外都相同,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后不放回,摸出黑色小球为赢,这个游戏( )
A.公平
B.不公平
C.先摸者赢的可能性大
D.后摸者赢的可能性大
A
典题精讲
6
在联欢会上,有A、B、C 三名选手站在一个三角形的三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个凳子,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC 的( )
A.三边上中线的交点
B.三边垂直平分线的交点
C.三条角平分线的交点
D.三边上高的交点
B
探索新知
2
知识点
修改规则对事件的影响
欢欢、乐乐想利用摸球的方式决定谁获胜,他们规定只摸一次,并且每次从6个球中摸出一个,欢欢将它们分别标上号码1,2,3,4,5,6,说:“你摸吧,只要你摸到了号码为6的球,你就胜,否则我就胜.”乐乐说:“不,还是你先摸吧,只要你摸到号码为1或2中的任意一个球,你就胜,否则我胜.”
(1)他们的规定公平吗?为什么?
(2)请你设计一种方案,在其他条件不变的情况下,只改变谁胜的规则,把这个游戏变公平.
例2
要想使游戏公平,就要保证每个事件发生的概率是相同的,否则就不公平.
导引:
探索新知
(1)它们的规定不公平.
因为在6个球中,只有一个号码为6的球,摸一次,摸到号码为6的球的概率是 ,没摸到的概率是 ,这样显然对乐乐不利,同样摸到1号球或2号球中的任意一个球的概率是 ,而摸不到的概率是 ,这显然对欢欢不利.
(2)规定摸到球的号码是奇数时,欢欢胜,摸到球的号码是偶数时,乐乐胜.
解:
探索新知
总 结
在判断游戏规则是否公平时,要分析规则中每一种情形发生的概率的大小,概率相等就公平,否则就不公平.(2)的设计方案不唯一.
典题精讲
1
如图所示的转盘,三个扇形的圆心角都相等,转动圆盘,等停下时观察指针停下的区域.
甲的观点:如果前3次指针都停在蓝色区
域,下 一次停在蓝色区域的概率会变大.
乙的观点:重复试验3次,一定会有一次停在蓝色区域.
丙的观点:指针停在红、黄、蓝三个区域的概率相等.
你认为谁的观点是正确的
丙的观点是正确的.
解:
典题精讲
2
小明与小刚一起玩抛掷两枚硬币的游戏,游戏规则:抛出两个正面——小明赢1分;抛出其他结果——小刚赢1分;谁先得到10分,谁就获胜.这是个不公平的游戏规则,要把它修改成公平的游戏,下列做法中错误的是( )
A.把“抛出两个正面”改为“抛出两个同面”
B.把“抛出其他结果”改为“抛出两个反面”
C.把“小明赢1分”改为“小明赢3分”
D.把“小刚赢1分”改为“小刚赢3分”
D
典题精讲
3
“抢30”游戏,规则是:第一人先说“1”或“1,2”,第二人要接着往下说一个或两个数,然后又轮到第一人,再接着往下说一个或两个数,这样两个人反复轮流,每次每人说一个或两个数都可以,但不可以连说三个数,谁先抢到30,谁就获胜.若按同样的规则改为抢“40”,其结果是( )
A.后报数者胜 B.先报数者胜
C.两者都可能胜 D.很难预料
B
易错提醒
暑假快到了,父母打算带兄妹俩去某个景点旅游一次,长长见识,可哥哥坚持去黄山,妹妹坚持去泰山,争执不下,父母为了公平起见,决定设计一个游戏,若哥哥赢了就去黄山,妹妹赢了就去泰山.下列游戏中,不能选用的是( )
A.掷一枚硬币,正面向上哥哥赢,反面向上妹妹赢
B.同时掷两枚硬币,两枚都正面向上,哥哥赢,一正一反向上妹妹赢
C.掷一枚骰子,向上的一面是奇数则哥哥赢,反之妹妹赢
D.在不透明的袋子中有两黑两红四个球,除颜色外,其余均相同,随机摸出
一个是黑球则哥哥赢,是红球则妹妹赢
B
易错点:对事件出现情况判断不全面而致错.
学以致用
小试牛刀
1
小明、小颖和小凡都想去看文博会,但现在只有一张门票,三人决定一起做游戏,谁获胜谁就去,游戏规则是:同时掷两枚质地均匀的硬币,若两枚正面朝上,则小明获胜,若两枚反面朝上,则小颖获胜;若一枚正面朝上,一枚反面朝上,则小凡获胜,关于这个游戏,下列判断正确的是( )
A.三人获胜的概率相同 B.小明获胜的概率大
C.小颖获胜的概率大 D.小凡获胜的概率大
D
小试牛刀
2
如图,小明、小刚利用两个转盘玩游戏,规则为小明将两个转盘各转一次,如配成紫色(红与蓝)得5分,否则小刚得3分,此规则( )
A.公平
B.对小明有利
C.对小刚有利
D.不可预测对谁有利
A
小试牛刀
3
在“抢30”的游戏中,如果将游戏规则中“不可以连说三个数,谁先抢到30,谁就获胜”,改为“每次最多可以连说三个数,谁先抢到33,谁就获胜.”那么采取适当策略,其结果是( )
A.先说数者胜 B.后说数者胜
C.两者都能胜 D.无法判断
A
小试牛刀
如图,小明和小亮用两个可以自由转动的转盘做游戏,每个转盘被分成
面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则
小明胜;否则小亮胜.这个游戏对双方公平吗?请说明理由.
小试牛刀
这个游戏对双方是公平的.理由如下:
列表得:
由表可知一共有6种等可能的情况,积大于2的有3种,
∴P (两次数字之积大于2)= = . ∴P (小明胜)= .
∴P (小亮胜)=1- = . ∵ = ,
∴这个游戏对双方是公平的.
解:
B A 积 1 2 3
1 1 2 3
2 2 4 6
小试牛刀
小红、小黄想利用摸球的方法决定谁看电影,规定只摸一次,每次摸一个球,已知不透明的袋子里有6个除颜色不同外其他完全一样的小球,上面分别标有数字1,2,3,4,5,6.两人商议了两种规则:
规则一:如果摸到了数字6,小红去,如果摸到的不是数字6,小黄去;
规则二:如果摸到数字1,2中的任意一个,小黄去,如果摸到的既不是1
也不是2,小红去.请你分析,这两个规则哪个公平?为什么?如果不公
平,请你修改这个规则使其公平.
小试牛刀
解:
规则一不公平,对小黄有利.理由如下:根据摸球方法,P (摸到数字6)= ,P (摸不到数字6)= .因为 > ,小黄去的概率大于小红去的概率,所以游戏规则不公平.规则二不公平,对小红有利.理由如下:根据摸球方法,
P (摸到数字1或2)= = ,P (摸不到数字1且摸不到数字2)= = .因为 > ,小红去的概率大于小黄去的概率,所以游戏规则不公平.修改方法不唯一,如:如果摸到的数字是奇数,小红去,如果摸到的数字是偶数,小黄去.
小试牛刀
一个盒子里有标号分别为1,2,3,4,5,6的六个小球,这些小球
除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率.
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出
一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸
出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或
同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙
赢.请用列表或画树形图的方法说明这个游戏对甲、乙两人是否公平.
小试牛刀
(1)摸到标号数字为奇数的小球的概率为 = .
(2)画树形图如图所示:
由树形图可知共有36种等可能的结果,两次摸到小球的
标号数字同为奇数或同为偶数的有18种,两次摸到小球
的标号数字为一奇一偶的也有18种,
∴P (甲赢)= = ,P (乙赢)= = .
∴这个游戏对甲、乙两人是公平的.
解:
小试牛刀
7 一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、乙两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树形图或列表的方法列出所有可能的结果.
(2)这样的游戏规则是否公平?请说明理由.
小试牛刀
(1)画树形图如图所示:
共有6种等可能的结果.
(2)游戏规则不公平,理由如下:
由树形图可知甲获胜的概率为 ,乙获胜的概率为 ,
所以乙获胜的可能性大,
所以这样的游戏规则不公平.
解:
课堂小结
课堂小结
1.概率是反映事件发生可能性大小的一般规律,同一个事件可能发生的概率与不可能发生的概率之和为1.
2.在机会游戏中,判断游戏对甲、乙两人是否公平,即分别求出甲、乙两人获胜事件的概率,若两个事件的概率相等,则游戏公平,若两个事件的概率不相等,则游戏不公平.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
31.2 随机事件的概率
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于2的概率是多少
新课精讲
探索新知
1
知识点
用概率说明事件的合理性
用概率说明普通游戏是否公平,关键看获胜的概率是否相同,相同则公平,不相同则不公平.
探索新知
“如图,是一个木制圆盘,供甲、乙掷飞镖用.图中是两同心圆,其中大圆的直径为20 cm,小圆的直径为10 cm,规定:若飞镖掷于小圆内(阴影部分),甲得2分;若飞镖掷于圆环内(白色部分),乙得1分,最后按所得分数定输赢.你认为此游戏公平吗?通过计算说明理由.
例1
探索新知
游戏是否公平,关键要看游戏双方取胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.但要注意本题是按所得分数定输赢,而掷于小圆内甲的得分与掷于圆环内乙的得分不相等.
导引:
经计算可知,阴影部分的面积为78.5 cm2,白色部分的面积为235.5 cm2. 所以飞镖掷于圆环内的概率等于掷于小圆内的概率的3倍,而掷于小圆内甲的得分却是掷于圆环内乙的得分的2倍,所以这个游戏不公平.
解:
探索新知
总 结
判断游戏的公平性是通过概率来判断的,如果对于参加游戏的每一个人获胜的概率相等,则游戏公平,否则不公平.
典题精讲
1
甲、乙两人做掷硬币游戏. 掷一枚质地均匀的硬币,落地后,正而朝上,甲胜;反面朝上,乙胜.共掷了10次硬币,结果有6次正面朝上,4次反面朝上. 乙认为这个游戏不公平你同意他的看法吗?请说说你理由.
不同意.理由:因为掷一枚硬币出现正面朝上和反面朝上的概率均为 ,所以这个游戏是公平的.
解:
典题精讲
2
足球比赛前,裁判断通常要掷一枚硬币来决定比赛双方的场地与首先发球者,其主要原因是( )
A.让比赛更富有情趣
B.让比赛更具有神秘色彩
C.体现比赛的公平性
D.让比赛更有挑战性
C
典题精讲
3
甲乙两人玩一个游戏,判定这个游戏公平的标准是( )
A.游戏的规则由甲方确定
B.游戏的规则由乙方确定
C.游戏的规则由甲乙双方商定
D.游戏双方要各有50%赢的机会
D
典题精讲
4
同时抛掷两枚质地均匀的硬币,则下列事件发生的概率最大的是( )
A.两正面都朝上
B.两背面都朝上
C.一个正面朝上,另一个背面朝上
D.三种情况发生的概率一样大
C
典题精讲
5
一个箱子中装有红、黄、黑三个小球,这些球除颜色外都相同,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后不放回,摸出黑色小球为赢,这个游戏( )
A.公平
B.不公平
C.先摸者赢的可能性大
D.后摸者赢的可能性大
A
典题精讲
6
在联欢会上,有A、B、C 三名选手站在一个三角形的三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个凳子,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC 的( )
A.三边上中线的交点
B.三边垂直平分线的交点
C.三条角平分线的交点
D.三边上高的交点
B
探索新知
2
知识点
修改规则对事件的影响
欢欢、乐乐想利用摸球的方式决定谁获胜,他们规定只摸一次,并且每次从6个球中摸出一个,欢欢将它们分别标上号码1,2,3,4,5,6,说:“你摸吧,只要你摸到了号码为6的球,你就胜,否则我就胜.”乐乐说:“不,还是你先摸吧,只要你摸到号码为1或2中的任意一个球,你就胜,否则我胜.”
(1)他们的规定公平吗?为什么?
(2)请你设计一种方案,在其他条件不变的情况下,只改变谁胜的规则,把这个游戏变公平.
例2
要想使游戏公平,就要保证每个事件发生的概率是相同的,否则就不公平.
导引:
探索新知
(1)它们的规定不公平.
因为在6个球中,只有一个号码为6的球,摸一次,摸到号码为6的球的概率是 ,没摸到的概率是 ,这样显然对乐乐不利,同样摸到1号球或2号球中的任意一个球的概率是 ,而摸不到的概率是 ,这显然对欢欢不利.
(2)规定摸到球的号码是奇数时,欢欢胜,摸到球的号码是偶数时,乐乐胜.
解:
探索新知
总 结
在判断游戏规则是否公平时,要分析规则中每一种情形发生的概率的大小,概率相等就公平,否则就不公平.(2)的设计方案不唯一.
典题精讲
1
如图所示的转盘,三个扇形的圆心角都相等,转动圆盘,等停下时观察指针停下的区域.
甲的观点:如果前3次指针都停在蓝色区
域,下 一次停在蓝色区域的概率会变大.
乙的观点:重复试验3次,一定会有一次停在蓝色区域.
丙的观点:指针停在红、黄、蓝三个区域的概率相等.
你认为谁的观点是正确的
丙的观点是正确的.
解:
典题精讲
2
小明与小刚一起玩抛掷两枚硬币的游戏,游戏规则:抛出两个正面——小明赢1分;抛出其他结果——小刚赢1分;谁先得到10分,谁就获胜.这是个不公平的游戏规则,要把它修改成公平的游戏,下列做法中错误的是( )
A.把“抛出两个正面”改为“抛出两个同面”
B.把“抛出其他结果”改为“抛出两个反面”
C.把“小明赢1分”改为“小明赢3分”
D.把“小刚赢1分”改为“小刚赢3分”
D
典题精讲
3
“抢30”游戏,规则是:第一人先说“1”或“1,2”,第二人要接着往下说一个或两个数,然后又轮到第一人,再接着往下说一个或两个数,这样两个人反复轮流,每次每人说一个或两个数都可以,但不可以连说三个数,谁先抢到30,谁就获胜.若按同样的规则改为抢“40”,其结果是( )
A.后报数者胜 B.先报数者胜
C.两者都可能胜 D.很难预料
B
易错提醒
暑假快到了,父母打算带兄妹俩去某个景点旅游一次,长长见识,可哥哥坚持去黄山,妹妹坚持去泰山,争执不下,父母为了公平起见,决定设计一个游戏,若哥哥赢了就去黄山,妹妹赢了就去泰山.下列游戏中,不能选用的是( )
A.掷一枚硬币,正面向上哥哥赢,反面向上妹妹赢
B.同时掷两枚硬币,两枚都正面向上,哥哥赢,一正一反向上妹妹赢
C.掷一枚骰子,向上的一面是奇数则哥哥赢,反之妹妹赢
D.在不透明的袋子中有两黑两红四个球,除颜色外,其余均相同,随机摸出
一个是黑球则哥哥赢,是红球则妹妹赢
B
易错点:对事件出现情况判断不全面而致错.
学以致用
小试牛刀
1
小明、小颖和小凡都想去看文博会,但现在只有一张门票,三人决定一起做游戏,谁获胜谁就去,游戏规则是:同时掷两枚质地均匀的硬币,若两枚正面朝上,则小明获胜,若两枚反面朝上,则小颖获胜;若一枚正面朝上,一枚反面朝上,则小凡获胜,关于这个游戏,下列判断正确的是( )
A.三人获胜的概率相同 B.小明获胜的概率大
C.小颖获胜的概率大 D.小凡获胜的概率大
D
小试牛刀
2
如图,小明、小刚利用两个转盘玩游戏,规则为小明将两个转盘各转一次,如配成紫色(红与蓝)得5分,否则小刚得3分,此规则( )
A.公平
B.对小明有利
C.对小刚有利
D.不可预测对谁有利
A
小试牛刀
3
在“抢30”的游戏中,如果将游戏规则中“不可以连说三个数,谁先抢到30,谁就获胜”,改为“每次最多可以连说三个数,谁先抢到33,谁就获胜.”那么采取适当策略,其结果是( )
A.先说数者胜 B.后说数者胜
C.两者都能胜 D.无法判断
A
小试牛刀
如图,小明和小亮用两个可以自由转动的转盘做游戏,每个转盘被分成
面积相等的几个扇形.转动两个转盘各一次,若两次数字之积大于2,则
小明胜;否则小亮胜.这个游戏对双方公平吗?请说明理由.
小试牛刀
这个游戏对双方是公平的.理由如下:
列表得:
由表可知一共有6种等可能的情况,积大于2的有3种,
∴P (两次数字之积大于2)= = . ∴P (小明胜)= .
∴P (小亮胜)=1- = . ∵ = ,
∴这个游戏对双方是公平的.
解:
B A 积 1 2 3
1 1 2 3
2 2 4 6
小试牛刀
小红、小黄想利用摸球的方法决定谁看电影,规定只摸一次,每次摸一个球,已知不透明的袋子里有6个除颜色不同外其他完全一样的小球,上面分别标有数字1,2,3,4,5,6.两人商议了两种规则:
规则一:如果摸到了数字6,小红去,如果摸到的不是数字6,小黄去;
规则二:如果摸到数字1,2中的任意一个,小黄去,如果摸到的既不是1
也不是2,小红去.请你分析,这两个规则哪个公平?为什么?如果不公
平,请你修改这个规则使其公平.
小试牛刀
解:
规则一不公平,对小黄有利.理由如下:根据摸球方法,P (摸到数字6)= ,P (摸不到数字6)= .因为 > ,小黄去的概率大于小红去的概率,所以游戏规则不公平.规则二不公平,对小红有利.理由如下:根据摸球方法,
P (摸到数字1或2)= = ,P (摸不到数字1且摸不到数字2)= = .因为 > ,小红去的概率大于小黄去的概率,所以游戏规则不公平.修改方法不唯一,如:如果摸到的数字是奇数,小红去,如果摸到的数字是偶数,小黄去.
小试牛刀
一个盒子里有标号分别为1,2,3,4,5,6的六个小球,这些小球
除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率.
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出
一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸
出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或
同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙
赢.请用列表或画树形图的方法说明这个游戏对甲、乙两人是否公平.
小试牛刀
(1)摸到标号数字为奇数的小球的概率为 = .
(2)画树形图如图所示:
由树形图可知共有36种等可能的结果,两次摸到小球的
标号数字同为奇数或同为偶数的有18种,两次摸到小球
的标号数字为一奇一偶的也有18种,
∴P (甲赢)= = ,P (乙赢)= = .
∴这个游戏对甲、乙两人是公平的.
解:
小试牛刀
7 一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、乙两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树形图或列表的方法列出所有可能的结果.
(2)这样的游戏规则是否公平?请说明理由.
小试牛刀
(1)画树形图如图所示:
共有6种等可能的结果.
(2)游戏规则不公平,理由如下:
由树形图可知甲获胜的概率为 ,乙获胜的概率为 ,
所以乙获胜的可能性大,
所以这样的游戏规则不公平.
解:
课堂小结
课堂小结
1.概率是反映事件发生可能性大小的一般规律,同一个事件可能发生的概率与不可能发生的概率之和为1.
2.在机会游戏中,判断游戏对甲、乙两人是否公平,即分别求出甲、乙两人获胜事件的概率,若两个事件的概率相等,则游戏公平,若两个事件的概率不相等,则游戏不公平.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
