【班海精品】冀教版(新)九下-31.3 用频率估计概率 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-31.3 用频率估计概率 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 09:33:47 | ||
图片预览








文档简介
(共41张PPT)
31.3 用频率估计概率
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么是频率?什么是概率?
2.同一事件的频率和概率相等吗?
3.上节课的抛硬币试验中频率是稳定的吗?概率呢?
4.上节课的抛硬币试验中频率的波动与试验次数有什么关系?
知识回顾
新课精讲
探索新知
1
知识点
用频率估计概率
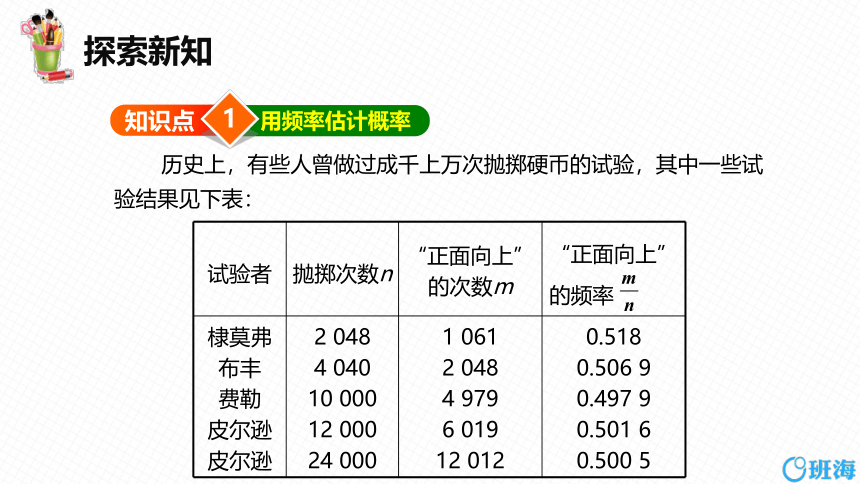
历史上,有些人曾做过成千上万次抛掷硬币的试验,其中一些试验结果见下表:
试验者 抛掷次数n “正面向上”
的次数m “正面向上”
的频率
棣莫弗 布丰 费勒 皮尔逊 皮尔逊 2 048 4 040 10 000 12 000 24 000 1 061 2 048 4 979 6 019 12 012 0.518
0.506 9
0.497 9
0.501 6
0.500 5
探索新知
根据表中数据,描出对应的点,如图:
思考:
随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
探索新知
归 纳
对一般的随机事件在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性,因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
探索新知
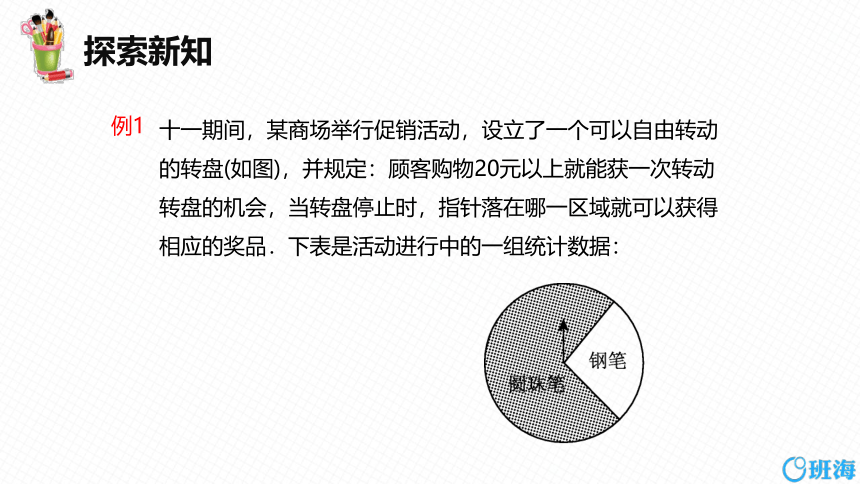
十一期间,某商场举行促销活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物20元以上就能获一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
例1
探索新知
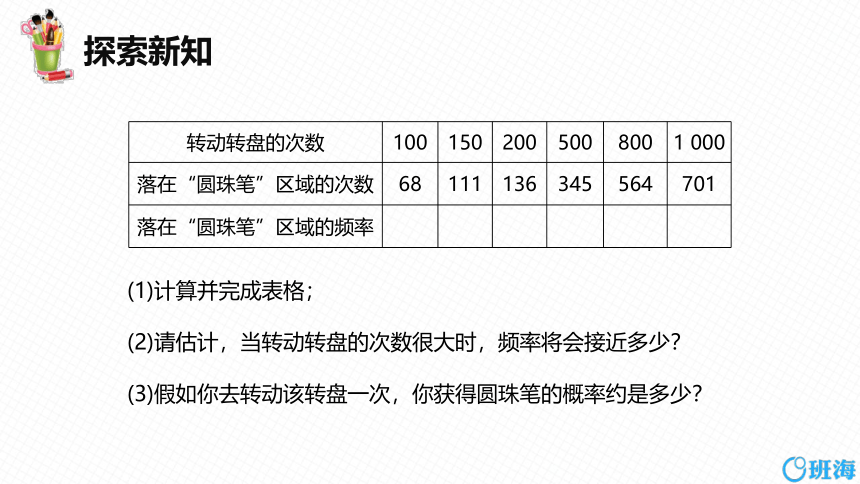
转动转盘的次数 100 150 200 500 800 1 000
落在“圆珠笔”区域的次数 68 111 136 345 564 701
落在“圆珠笔”区域的频率
(1)计算并完成表格;
(2)请估计,当转动转盘的次数很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得圆珠笔的概率约是多少?
探索新知
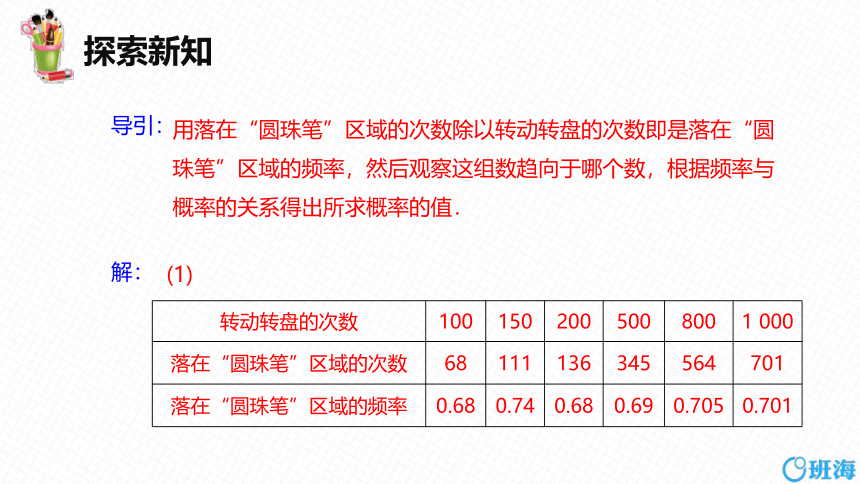
用落在“圆珠笔”区域的次数除以转动转盘的次数即是落在“圆珠笔”区域的频率,然后观察这组数趋向于哪个数,根据频率与概率的关系得出所求概率的值.
导引:
(1)
解:
转动转盘的次数 100 150 200 500 800 1 000
落在“圆珠笔”区域的次数 68 111 136 345 564 701
落在“圆珠笔”区域的频率 0.68 0.74 0.68 0.69 0.705 0.701
探索新知
(2)当转动转盘的次数很大时,频率将会接近0.7.
(3)获得圆珠笔的概率约是0.7.
探索新知
总 结
本题体现了由样本估计总体的统计思想.不过只有在试验次数足够多时,才能用事件的频率估计概率.
典题精讲
某种化妆品经销商随机访问了4名顾客,结果有3人使用X品牌的化妆品. 经销商宣称:“X品牌化妆品的市场占有率为75%.”这个结论可信吗?
1
解:这个结论不可信.因为随机访问的人数太少,75%不能代
表X品牌化妆品的市场占有率.
典题精讲
某地区在2009年至2013年5年间,共出生婴儿29362人,其中男婴14900人. 据此分别估计该地区生男孩和生女孩的概率.
2
解:P(生男孩)= ≈0.51,
P(生女孩)≈1-0.51=0.49.
典题精讲
某种油菜籽在相同条件下发芽试验的结果如下表:
3
每批粒 数n 100 300 400 600 1 000 2 000 3 000
发芽的 频数m 96 284 380 571 948 1 902 2 848
发芽的 频率 0.960 0.947 0.950 0.952 0.948 0.951 0.949
那么估计这种油菜籽发芽的概率是________(结果精确到0.01).
0.95
典题精讲
在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法来估算正面朝上的概率,其试验次数分别为10次、50次、100次、200次,其中试验相对科学的是( )
A.甲组 B.乙组
C.丙组 D.丁组
4
D
探索新知
2
知识点
频率与概率的关系
频率与概率的关系:在大量重复试验中,如果事件A 发生的频率 稳定于某个常数b,则该事件发生的概率P (A)= ____.
b
(1)当试验次数很多时,一个事件发生的频率稳定在相应的概率附近.
(2)频率是通过试验得到的一个数据结果,因试验次数的不同而有所改变,是一个实际的具体值.概率是一个事件发生的可能性大小的理论值,它不因试验次数的改变而变化,是一个常数.
探索新知
关于频率和概率的关系,下列说法正确的是( )
A.频率等于概率
B.当试验次数很大时,频率稳定在概率附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
例2
A.频率只能估计概率;B.正确;C.概率是定值;D.可以相同,如“抛硬币试验”,可得到正面向上的频率为0.5,与概率相同.故选B.
导引:
B
探索新知
总 结
用频率估计概率的方法:
利用频率估计概率时,不能以某一次试验的结果作为估计的概率,试验的次数越多,用频率估计概率也越准确,因此用多次试验后的频率的稳定值估计概率.
在做大量重复试验时,某事件发生的频率会稳定在某个常数的附近,这个常数就叫做事件概率的估计值,而不是一种必然的结果.
典题精讲
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
1
D
典题精讲
用频率估计概率,可以发现,抛掷硬币“正面朝上”的概率为0.5是指( )
A.连续掷2次,结果一定是“正面朝上”和 “反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次硬币,恰好有n 次“正面朝上”
D.抛掷n 次,当n 越来越大时,正面朝上的频率会越来越稳定于0.5
2
D
典题精讲
在“拋掷正六面体”的试验中,正六面体的六个面分别标有数字1,2,3,4,5,6,如果试验的次数增多,出现数字6的频率的变化趋势是接近________.
3
易错提醒
下列说法合理的是( )
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他
说钉尖朝上的概率是30%
B.抛掷一枚普通的正六面体骰子,出现6点朝上的概率
是 的意思是每掷6次就有1次掷得6点朝上
C.某彩票的中奖机会是2%,那么如果买100张彩票一定
会有2张中奖
D.在一次课堂进行的试验中,甲、乙两组同学估计硬币
落地后,正面朝上的概率分别为0.48和0.51
D
易错提醒
诊断:用频率估计概率时,要注意试验的次数越多,事件
发生的频率就会越接近于这个事件发生的概率,试
验的次数太少,易受偶然性因素影响,此时的频率
不能用来估计概率.
易错点:不能正确理解频率与概率的关系.
学以致用
小试牛刀
在一个不透明的盒子中装有a 个除颜色外完全相同的球,这a 个球中只有3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a 的值约为( )
A.12 B.15
C.18 D.21
1
B
小试牛刀
在一个不透明的盒子中有20个除颜色外均相同的小球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒子中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4附近,由此可估计盒子中红球的个数为( )
A.4 B.6
C.8 D.12
2
C
小试牛刀
甲、乙两名同学在一次用频率去估计概率的试验中,统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A.掷一枚正六面体的骰子,出现1点的概率
B.从一个装有2个白球和1个红球的袋子中任取1个球,取到红球的概率
C.拋一枚硬币,出现正面
朝上的概率
D.任意写一个整数,它能
被2整除的概率
3
B
小试牛刀
4 王老师将1个黑球和若干个白球(每个球除颜色外都相同)放
入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每
次摸出一个球(有放回),下表是试验进行中的一组统计数据.
(1)补全上表中的有关数据,根据上表数据估计从口袋中摸出
一个球是黑球的概率是________;
(2)估算口袋中白球的个数;
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用
画树形图或列表的方法计算他两次都摸出白球的概率.
摸球的次数n 100 150 200 500 800 1 000
摸到黑球的次数m 23 31 60 130 203 251
摸到黑球的频率 0.23 0.21 0.30 0.26 0.25
0.25
0.25
小试牛刀
251÷1 000=0.251,保留两位小数,表格中应填0.25;
∵大量重复试验事件发生的频率逐渐稳定到0.25附近,∴估计从口袋中摸出一个球是黑球的概率是0.25.
小试牛刀
(2)设口袋中白球为x 个,由题意得 =0.25,
解得x=3.经检验,x=3符合题意.
∴估计口袋中有3个白球.
(3)用B代表黑球,W1,W2,W3代表白球,将摸球情况列表
如下:
总共有16种等可能的结果,其中两个球都是白球的结果有9种,所以两次都摸出白球的概率为 .
解:
第二次 第一次 B W1 W2 W3
B (B,B) (B,W1) (B,W2) (B,W3)
W1 (W1,B) (W1,W1) (W1,W2) (W1,W3)
W2 (W2,B) (W2,W1) (W2,W2) (W2,W3)
W3 (W3,B) (W3,W1) (W3,W2) (W3,W3)
小试牛刀
为了解学生的体能情况,随机选取了1 000名学生进行调查,并记录了
他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统
计表,其中“√”表示喜欢,“×”表示不喜欢.
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑,则该学生同时喜欢短跑、跳绳、跳远中哪项的
可能性最大?
项目学生数 长跑 短跑 跳绳 跳远
200 √ × √ √
300 × √ × √
150 √ √ √ ×
200 √ × √ ×
150 √ × × ×
小试牛刀
(1)估计学生同时喜欢短跑和跳绳的概率为 = .
(2)估计学生同时喜欢三个项目的概率为 =
(3)喜欢长跑的700名学生中,有150名学生喜欢短跑,550名学
生喜欢跳绳,200名学生喜欢跳远,于是喜欢长跑的学生同时
喜欢跳绳的可能性最大.
解:
小试牛刀
国务院办公厅在2015年3月16日发布了《中国足球改革的总体方案》,
这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球
文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普
及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)a=_____,b=_____;并补全频数分布直方图.
获奖等次 频数 频率
一等奖 10 0.05
二等奖 20 0.10
三等奖 30 b
优胜奖 a 0.30
鼓励奖 80 0.40
小试牛刀
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树形图或列表的方法,计算恰好选中甲、乙二人的概率.
小试牛刀
(1)60;0.15
补全频数分布直方图如图所示.
(2)360°×0.30=108°.所以获得优胜奖对应的扇形圆心角的度数是108°.
解:
小试牛刀
(3)列表如下:
由表格可知共有12种等可能的结果,其中恰好选中甲、乙二人的有2种,故所求的概率为 = .
甲 乙 丙 丁
甲 甲、乙 甲、丙 甲、丁
乙 乙、甲 乙、丙 乙、丁
丙 丙、甲 丙、乙 丙、丁
丁 丁、甲 丁、乙 丁、丙
课堂小结
课堂小结
通过本课时的学习,需要我们掌握:
1.用频率估计概率的条件及方法,应用以上的内容解决一些实际问题.
2.从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,可以发现:在大量的偶然之中存在着必然的规律.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
31.3 用频率估计概率
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么是频率?什么是概率?
2.同一事件的频率和概率相等吗?
3.上节课的抛硬币试验中频率是稳定的吗?概率呢?
4.上节课的抛硬币试验中频率的波动与试验次数有什么关系?
知识回顾
新课精讲
探索新知
1
知识点
用频率估计概率
历史上,有些人曾做过成千上万次抛掷硬币的试验,其中一些试验结果见下表:
试验者 抛掷次数n “正面向上”
的次数m “正面向上”
的频率
棣莫弗 布丰 费勒 皮尔逊 皮尔逊 2 048 4 040 10 000 12 000 24 000 1 061 2 048 4 979 6 019 12 012 0.518
0.506 9
0.497 9
0.501 6
0.500 5
探索新知
根据表中数据,描出对应的点,如图:
思考:
随着抛掷次数的增加,“正面向上”的频率的变化趋势是什么?
探索新知
归 纳
对一般的随机事件在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性,因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
探索新知
十一期间,某商场举行促销活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物20元以上就能获一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
例1
探索新知
转动转盘的次数 100 150 200 500 800 1 000
落在“圆珠笔”区域的次数 68 111 136 345 564 701
落在“圆珠笔”区域的频率
(1)计算并完成表格;
(2)请估计,当转动转盘的次数很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得圆珠笔的概率约是多少?
探索新知
用落在“圆珠笔”区域的次数除以转动转盘的次数即是落在“圆珠笔”区域的频率,然后观察这组数趋向于哪个数,根据频率与概率的关系得出所求概率的值.
导引:
(1)
解:
转动转盘的次数 100 150 200 500 800 1 000
落在“圆珠笔”区域的次数 68 111 136 345 564 701
落在“圆珠笔”区域的频率 0.68 0.74 0.68 0.69 0.705 0.701
探索新知
(2)当转动转盘的次数很大时,频率将会接近0.7.
(3)获得圆珠笔的概率约是0.7.
探索新知
总 结
本题体现了由样本估计总体的统计思想.不过只有在试验次数足够多时,才能用事件的频率估计概率.
典题精讲
某种化妆品经销商随机访问了4名顾客,结果有3人使用X品牌的化妆品. 经销商宣称:“X品牌化妆品的市场占有率为75%.”这个结论可信吗?
1
解:这个结论不可信.因为随机访问的人数太少,75%不能代
表X品牌化妆品的市场占有率.
典题精讲
某地区在2009年至2013年5年间,共出生婴儿29362人,其中男婴14900人. 据此分别估计该地区生男孩和生女孩的概率.
2
解:P(生男孩)= ≈0.51,
P(生女孩)≈1-0.51=0.49.
典题精讲
某种油菜籽在相同条件下发芽试验的结果如下表:
3
每批粒 数n 100 300 400 600 1 000 2 000 3 000
发芽的 频数m 96 284 380 571 948 1 902 2 848
发芽的 频率 0.960 0.947 0.950 0.952 0.948 0.951 0.949
那么估计这种油菜籽发芽的概率是________(结果精确到0.01).
0.95
典题精讲
在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法来估算正面朝上的概率,其试验次数分别为10次、50次、100次、200次,其中试验相对科学的是( )
A.甲组 B.乙组
C.丙组 D.丁组
4
D
探索新知
2
知识点
频率与概率的关系
频率与概率的关系:在大量重复试验中,如果事件A 发生的频率 稳定于某个常数b,则该事件发生的概率P (A)= ____.
b
(1)当试验次数很多时,一个事件发生的频率稳定在相应的概率附近.
(2)频率是通过试验得到的一个数据结果,因试验次数的不同而有所改变,是一个实际的具体值.概率是一个事件发生的可能性大小的理论值,它不因试验次数的改变而变化,是一个常数.
探索新知
关于频率和概率的关系,下列说法正确的是( )
A.频率等于概率
B.当试验次数很大时,频率稳定在概率附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
例2
A.频率只能估计概率;B.正确;C.概率是定值;D.可以相同,如“抛硬币试验”,可得到正面向上的频率为0.5,与概率相同.故选B.
导引:
B
探索新知
总 结
用频率估计概率的方法:
利用频率估计概率时,不能以某一次试验的结果作为估计的概率,试验的次数越多,用频率估计概率也越准确,因此用多次试验后的频率的稳定值估计概率.
在做大量重复试验时,某事件发生的频率会稳定在某个常数的附近,这个常数就叫做事件概率的估计值,而不是一种必然的结果.
典题精讲
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
1
D
典题精讲
用频率估计概率,可以发现,抛掷硬币“正面朝上”的概率为0.5是指( )
A.连续掷2次,结果一定是“正面朝上”和 “反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次硬币,恰好有n 次“正面朝上”
D.抛掷n 次,当n 越来越大时,正面朝上的频率会越来越稳定于0.5
2
D
典题精讲
在“拋掷正六面体”的试验中,正六面体的六个面分别标有数字1,2,3,4,5,6,如果试验的次数增多,出现数字6的频率的变化趋势是接近________.
3
易错提醒
下列说法合理的是( )
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他
说钉尖朝上的概率是30%
B.抛掷一枚普通的正六面体骰子,出现6点朝上的概率
是 的意思是每掷6次就有1次掷得6点朝上
C.某彩票的中奖机会是2%,那么如果买100张彩票一定
会有2张中奖
D.在一次课堂进行的试验中,甲、乙两组同学估计硬币
落地后,正面朝上的概率分别为0.48和0.51
D
易错提醒
诊断:用频率估计概率时,要注意试验的次数越多,事件
发生的频率就会越接近于这个事件发生的概率,试
验的次数太少,易受偶然性因素影响,此时的频率
不能用来估计概率.
易错点:不能正确理解频率与概率的关系.
学以致用
小试牛刀
在一个不透明的盒子中装有a 个除颜色外完全相同的球,这a 个球中只有3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a 的值约为( )
A.12 B.15
C.18 D.21
1
B
小试牛刀
在一个不透明的盒子中有20个除颜色外均相同的小球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒子中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4附近,由此可估计盒子中红球的个数为( )
A.4 B.6
C.8 D.12
2
C
小试牛刀
甲、乙两名同学在一次用频率去估计概率的试验中,统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A.掷一枚正六面体的骰子,出现1点的概率
B.从一个装有2个白球和1个红球的袋子中任取1个球,取到红球的概率
C.拋一枚硬币,出现正面
朝上的概率
D.任意写一个整数,它能
被2整除的概率
3
B
小试牛刀
4 王老师将1个黑球和若干个白球(每个球除颜色外都相同)放
入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每
次摸出一个球(有放回),下表是试验进行中的一组统计数据.
(1)补全上表中的有关数据,根据上表数据估计从口袋中摸出
一个球是黑球的概率是________;
(2)估算口袋中白球的个数;
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用
画树形图或列表的方法计算他两次都摸出白球的概率.
摸球的次数n 100 150 200 500 800 1 000
摸到黑球的次数m 23 31 60 130 203 251
摸到黑球的频率 0.23 0.21 0.30 0.26 0.25
0.25
0.25
小试牛刀
251÷1 000=0.251,保留两位小数,表格中应填0.25;
∵大量重复试验事件发生的频率逐渐稳定到0.25附近,∴估计从口袋中摸出一个球是黑球的概率是0.25.
小试牛刀
(2)设口袋中白球为x 个,由题意得 =0.25,
解得x=3.经检验,x=3符合题意.
∴估计口袋中有3个白球.
(3)用B代表黑球,W1,W2,W3代表白球,将摸球情况列表
如下:
总共有16种等可能的结果,其中两个球都是白球的结果有9种,所以两次都摸出白球的概率为 .
解:
第二次 第一次 B W1 W2 W3
B (B,B) (B,W1) (B,W2) (B,W3)
W1 (W1,B) (W1,W1) (W1,W2) (W1,W3)
W2 (W2,B) (W2,W1) (W2,W2) (W2,W3)
W3 (W3,B) (W3,W1) (W3,W2) (W3,W3)
小试牛刀
为了解学生的体能情况,随机选取了1 000名学生进行调查,并记录了
他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统
计表,其中“√”表示喜欢,“×”表示不喜欢.
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑,则该学生同时喜欢短跑、跳绳、跳远中哪项的
可能性最大?
项目学生数 长跑 短跑 跳绳 跳远
200 √ × √ √
300 × √ × √
150 √ √ √ ×
200 √ × √ ×
150 √ × × ×
小试牛刀
(1)估计学生同时喜欢短跑和跳绳的概率为 = .
(2)估计学生同时喜欢三个项目的概率为 =
(3)喜欢长跑的700名学生中,有150名学生喜欢短跑,550名学
生喜欢跳绳,200名学生喜欢跳远,于是喜欢长跑的学生同时
喜欢跳绳的可能性最大.
解:
小试牛刀
国务院办公厅在2015年3月16日发布了《中国足球改革的总体方案》,
这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球
文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普
及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)a=_____,b=_____;并补全频数分布直方图.
获奖等次 频数 频率
一等奖 10 0.05
二等奖 20 0.10
三等奖 30 b
优胜奖 a 0.30
鼓励奖 80 0.40
小试牛刀
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树形图或列表的方法,计算恰好选中甲、乙二人的概率.
小试牛刀
(1)60;0.15
补全频数分布直方图如图所示.
(2)360°×0.30=108°.所以获得优胜奖对应的扇形圆心角的度数是108°.
解:
小试牛刀
(3)列表如下:
由表格可知共有12种等可能的结果,其中恰好选中甲、乙二人的有2种,故所求的概率为 = .
甲 乙 丙 丁
甲 甲、乙 甲、丙 甲、丁
乙 乙、甲 乙、丙 乙、丁
丙 丙、甲 丙、乙 丙、丁
丁 丁、甲 丁、乙 丁、丙
课堂小结
课堂小结
通过本课时的学习,需要我们掌握:
1.用频率估计概率的条件及方法,应用以上的内容解决一些实际问题.
2.从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,可以发现:在大量的偶然之中存在着必然的规律.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
