【班海精品】冀教版(新)九下-32.1 投影 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-32.1 投影 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 09:33:47 | ||
图片预览









文档简介
(共39张PPT)
32.1 投影
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
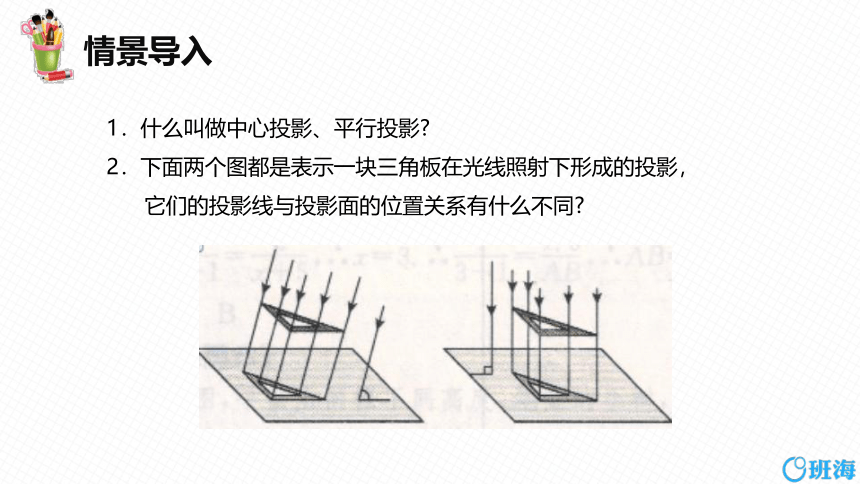
1.什么叫做中心投影、平行投影
2.下面两个图都是表示一块三角板在光线照射下形成的投影,
它们的投影线与投影面的位置关系有什么不同
新课精讲
探索新知
1
知识点
正投影的定义
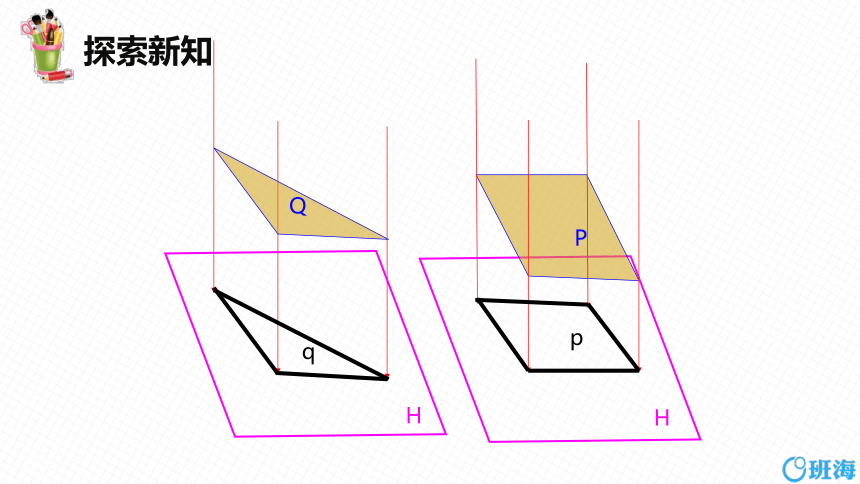
正投影法:
投影线与投影面垂直的平行投影法,所得的投影,称为正投影 .
探索新知
q
Q
H
P
H
p
探索新知
例1 如图所示的圆台的上下底面与投影线平行,圆台
的正投影是( )
A、矩形 B、两条线段
C、等腰梯形 D、圆环
根据正投影的定义及正投影形状分析.根据题意:
圆台的上下底面与投影线平行,则圆台的正投影是
该圆台的轴截面,即等腰梯形.故选C.
分析:
C
探索新知
总 结
物体的正投影的形状、大小与物体相对于投影面的位置有关.它分物体与投影面平行、倾斜、垂直三种情况.
1 投影线________于投影面产生的投影叫做正投影;它包含以下两个要素:
(1)正投影是特殊的____________,它不可能是___________.
(2)正投影只要求________与________垂直,与物体位置无关.
垂直
平行投影
中心投影
光线
投影面
典题精讲
球的正投影是( )
A.圆 B.椭圆
C.点 D.圆环
正方形的正投影不可能是( )
A.线段 B.矩形
C.正方形 D.梯形
2
3
A
D
典题精讲
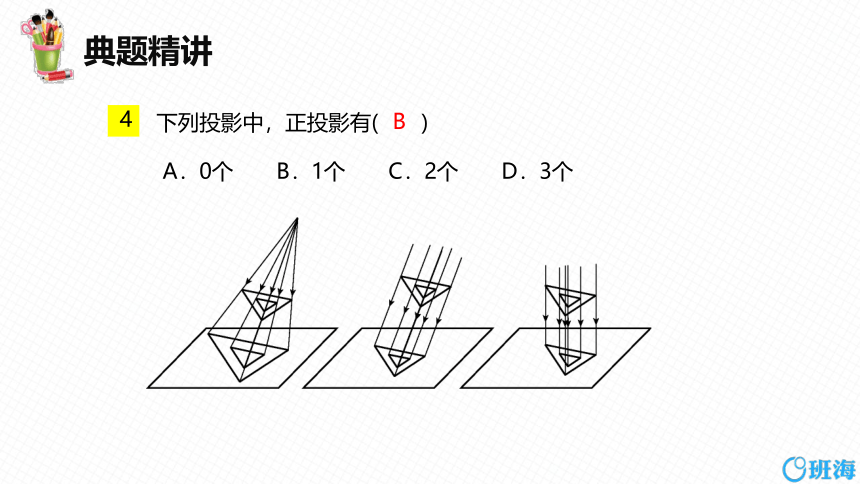
下列投影中,正投影有( )
A.0个 B.1个 C.2个 D.3个
4
B
典题精讲
典题精讲
如图,水杯的杯口与投影面平行,投影线的方向如箭头所
示,它的正投影是( )
D
探索新知
2
知识点
正投影的性质
如图,把一根直的细铁丝(记为线段AB )放在三个不同位置:
(1) 铁丝平行于投影面;
(2) 铁丝倾斜于投影面;
(3) 铁丝垂直于投影面(铁丝不一定要与投影面有交点).三种情形
下铁丝的正投影各是什么形状
探索新知
通过观察、测量可知:
(1)当线段AB 平行于投影面时,它的正投影是线段A1B1,
它们的大小关系为AB=A1B1;
(2)当线段AB 倾斜于投影面时,它的正投影是线段A2B2,
它们的大小关系为AB>A2B2;
(3)当线段AB 垂直于投影面时,它的正投影是一个点A3.
探索新知
如图,把一块正方形硬纸板P (记为正方形ABCD )放在三个不同位置:
纸板平行于投影面;
(2) 纸板倾斜于投影面;
(3) 纸板垂直于投影面.
三种情形下纸板的正投影各是什么形状
探索新知
通过观察、测量可知:
当纸板P 平行于投影面时,P 的正投影与P 的形状、大小一样;
当纸板P 倾斜于投影面时,P 的正投影与P 的形状、大小不完全一样;
(3) 当纸板P 垂直于投影面时,P 的正投影成为一条线段.
探索新知
总 结
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、 大小完全相同.
探索新知
例2 一根笔直的小木棒(记为线段AB )的正投影为线段CD,则下
列各式中一定成立的是( )
A.AB=CD B.AB≤CD
C.AB>CD D.AB≥CD
D
当AB 平行于投影面时,AB=CD;
当AB 倾斜于投影面时,AB>CD;
当AB 垂直于投影面时,正投影是一个点.
导引:
探索新知
总 结
物体的正投影的形状、大小与物体相对于投影面的位置有关.画一般立体图形的正投影的关键是找出平行于投影面的立体图形的最大截面.
典题精讲
1
A
小乐用一块矩形硬纸板在阳光下做投影实验,通过观察,发现这块矩形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形 B.线段
C.矩形 D.平行四边形
2
当棱长为20 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( )
A.200 cm2 B.300 cm2
C.400 cm2 D.600 cm2
C
典题精讲
几何体在平面P 的正投影,取决于( )
①几何体的形状;②投影面与几何体的位置关系;
③投影面P 的大小.
A.①② B.①③
C.②③ D.①②③
3
A
易错提醒
如图所示,把正方体一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光垂直,则正方体在纸上的正投影是( )
易错点:对正方体的正投影的类型认识不全而致错.
C
学以致用
小试牛刀
底面与投影面垂直的圆锥体的正投影是( )
A.圆 B.三角形
C.矩形 D.正方形
1
B
小试牛刀
把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( )
2
A
小试牛刀
如图,投影线的方向如箭头所示,画出下列各图形的正投影.
3
解:如图所示.
小试牛刀
4 已知一根长为8 cm的木棒 AB 与投影面平行,投影线垂
直于投影面.
(1)求此时的影子A1B1的长度;
(2)如图是将木棒绕其端点A逆时针旋转30°后的示意图
(此时平面ABB2A2垂直于投影面),求旋转后木棒的影子A2B2的长.
分析:
(1)当木棒平行于投影面时,其正投影的长度与木棒的长度一致;(2)当木棒倾斜于投影面时,可转化为解直角三角形来求解.
小试牛刀
(1)因为木棒平行于投影面,
所以A1B1=AB=8 cm,
即此时的影子A1B1的长度为8 cm.
(2)过点A 作AH⊥BB2于点H.
因为AA2⊥A2B2,BB2⊥A2B2,
所以四边形AA2B2H 为矩形,所以AH=A2B2.
在Rt△ABH 中,∠BAH=30°,AB=8 cm,
所以A2B2=AH=AB·cos 30°=8× =4 (cm).
即旋转后木棒的影子A2B2的长为4 cm.
解:
小试牛刀
5 已知一纸板的形状为正方形ABCD,且边长为10 cm.
如图,四边形A1B1C1D1是正方形ABCD 在面β上的正
投影,AD,BC 与投影面β 平行,且AB,CD 与投影
面β 成30°角,求正方形ABCD 的正投影的面积.
小试牛刀
解:
规律总结:求投影的面积,先确定投影的形状,再根据相
应的面积公式,有针对性地求出相关线段的长.
过点A 作AH⊥BB1于点H. 依题意,得∠BAH=30°,四边形A1B1C1D1是矩形,其中A1D1=AD,A1B1=AH.
∵AH⊥BB1,∠BAH=30°,∴AH=AB ·cos 30°=
10× =5(cm),∴A1B1=AH=5 cm.
∵A1D1=AD=10 cm,
∴S四边形A1B1C1D1=A1B1·A1D1=5 ×10=50 (cm2).
则正方形ABCD 的正投影的面积是50 cm2.
小试牛刀
一个圆锥的轴截面平行于投影面,圆锥的正投影是等腰三角形,
如图所示,等腰三角形的腰长为13 cm,高为12 cm,求该圆锥
的体积及表面积.(提示:V圆锥= πr 2h,其中r 是底面圆的半
径,h 是圆锥的高)
小试牛刀
解:
由于圆锥的轴截面平行于投影面,其正投影是等腰三角形,因此圆锥的高等于等腰三角形的高;圆锥底面圆的半径等于等腰三角形底边长的一半.如图,作AD⊥BC 于D,AB=AC=13 cm,AD=12 cm,∴CD=5 cm,
∴r=CD=5 cm,h=12 cm.
∴V圆锥= πr 2h=100π cm3,
底面周长为l=2πr=10π cm,
母线长R=AC=13 cm,
∴S表= lR+πr 2=90π cm2.
小试牛刀
7 操作与研究:
如图,△ABC 被平行光线照射,CD
⊥AB 于D,CD 与光线平行,AB 在投
影面上.
(1)指出图中AC 的投影是什么,CD 与BC 的投影呢?
(2)探究:当△ABC 为直角三角形(∠ACB=90°)时,易
得AC 2=AD ·AB,此时有如下结论:直角三角形一直
角边的平方等于它在斜边上的射影与斜边的乘积,这
一结论我们称为射影定理.
通过上述结论的推理,请证明以下两个结论:
①BC 2=BD ·AB;②CD 2=AD ·BD.
小试牛刀
(1)解:AC 的投影是AD,CD 的投影是点D,BC 的投影
是BD.
(2)证明:①易证得△BCD∽△BAC,可得BC 2=BD ·AB;
②易证得△ACD∽△CBD,可得CD 2=AD ·BD.
课堂小结
课堂小结
1.回顾正投影的含义及其性质;
2.反思作简单几何图形的正投影的过程及自己作图过程中失误的原因,体会正投影的作图方法与技巧;
3.物体的正投影的形状、大小与它相对于投影面的位置是否有关系?
课堂小结
平行投影与中心投影的区别与联系 联系 都是物体在光线的照射下,在某个平面内形成的影子,即都是投影 区 别 光线 中心投影 从一点发出的投射线
平行投影 平行的投射线
物体与投影面平行时的投影 中心投影 放大(位似变换)
平行投影 全等
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
32.1 投影
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么叫做中心投影、平行投影
2.下面两个图都是表示一块三角板在光线照射下形成的投影,
它们的投影线与投影面的位置关系有什么不同
新课精讲
探索新知
1
知识点
正投影的定义
正投影法:
投影线与投影面垂直的平行投影法,所得的投影,称为正投影 .
探索新知
q
Q
H
P
H
p
探索新知
例1 如图所示的圆台的上下底面与投影线平行,圆台
的正投影是( )
A、矩形 B、两条线段
C、等腰梯形 D、圆环
根据正投影的定义及正投影形状分析.根据题意:
圆台的上下底面与投影线平行,则圆台的正投影是
该圆台的轴截面,即等腰梯形.故选C.
分析:
C
探索新知
总 结
物体的正投影的形状、大小与物体相对于投影面的位置有关.它分物体与投影面平行、倾斜、垂直三种情况.
1 投影线________于投影面产生的投影叫做正投影;它包含以下两个要素:
(1)正投影是特殊的____________,它不可能是___________.
(2)正投影只要求________与________垂直,与物体位置无关.
垂直
平行投影
中心投影
光线
投影面
典题精讲
球的正投影是( )
A.圆 B.椭圆
C.点 D.圆环
正方形的正投影不可能是( )
A.线段 B.矩形
C.正方形 D.梯形
2
3
A
D
典题精讲
下列投影中,正投影有( )
A.0个 B.1个 C.2个 D.3个
4
B
典题精讲
典题精讲
如图,水杯的杯口与投影面平行,投影线的方向如箭头所
示,它的正投影是( )
D
探索新知
2
知识点
正投影的性质
如图,把一根直的细铁丝(记为线段AB )放在三个不同位置:
(1) 铁丝平行于投影面;
(2) 铁丝倾斜于投影面;
(3) 铁丝垂直于投影面(铁丝不一定要与投影面有交点).三种情形
下铁丝的正投影各是什么形状
探索新知
通过观察、测量可知:
(1)当线段AB 平行于投影面时,它的正投影是线段A1B1,
它们的大小关系为AB=A1B1;
(2)当线段AB 倾斜于投影面时,它的正投影是线段A2B2,
它们的大小关系为AB>A2B2;
(3)当线段AB 垂直于投影面时,它的正投影是一个点A3.
探索新知
如图,把一块正方形硬纸板P (记为正方形ABCD )放在三个不同位置:
纸板平行于投影面;
(2) 纸板倾斜于投影面;
(3) 纸板垂直于投影面.
三种情形下纸板的正投影各是什么形状
探索新知
通过观察、测量可知:
当纸板P 平行于投影面时,P 的正投影与P 的形状、大小一样;
当纸板P 倾斜于投影面时,P 的正投影与P 的形状、大小不完全一样;
(3) 当纸板P 垂直于投影面时,P 的正投影成为一条线段.
探索新知
总 结
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、 大小完全相同.
探索新知
例2 一根笔直的小木棒(记为线段AB )的正投影为线段CD,则下
列各式中一定成立的是( )
A.AB=CD B.AB≤CD
C.AB>CD D.AB≥CD
D
当AB 平行于投影面时,AB=CD;
当AB 倾斜于投影面时,AB>CD;
当AB 垂直于投影面时,正投影是一个点.
导引:
探索新知
总 结
物体的正投影的形状、大小与物体相对于投影面的位置有关.画一般立体图形的正投影的关键是找出平行于投影面的立体图形的最大截面.
典题精讲
1
A
小乐用一块矩形硬纸板在阳光下做投影实验,通过观察,发现这块矩形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形 B.线段
C.矩形 D.平行四边形
2
当棱长为20 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( )
A.200 cm2 B.300 cm2
C.400 cm2 D.600 cm2
C
典题精讲
几何体在平面P 的正投影,取决于( )
①几何体的形状;②投影面与几何体的位置关系;
③投影面P 的大小.
A.①② B.①③
C.②③ D.①②③
3
A
易错提醒
如图所示,把正方体一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光垂直,则正方体在纸上的正投影是( )
易错点:对正方体的正投影的类型认识不全而致错.
C
学以致用
小试牛刀
底面与投影面垂直的圆锥体的正投影是( )
A.圆 B.三角形
C.矩形 D.正方形
1
B
小试牛刀
把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( )
2
A
小试牛刀
如图,投影线的方向如箭头所示,画出下列各图形的正投影.
3
解:如图所示.
小试牛刀
4 已知一根长为8 cm的木棒 AB 与投影面平行,投影线垂
直于投影面.
(1)求此时的影子A1B1的长度;
(2)如图是将木棒绕其端点A逆时针旋转30°后的示意图
(此时平面ABB2A2垂直于投影面),求旋转后木棒的影子A2B2的长.
分析:
(1)当木棒平行于投影面时,其正投影的长度与木棒的长度一致;(2)当木棒倾斜于投影面时,可转化为解直角三角形来求解.
小试牛刀
(1)因为木棒平行于投影面,
所以A1B1=AB=8 cm,
即此时的影子A1B1的长度为8 cm.
(2)过点A 作AH⊥BB2于点H.
因为AA2⊥A2B2,BB2⊥A2B2,
所以四边形AA2B2H 为矩形,所以AH=A2B2.
在Rt△ABH 中,∠BAH=30°,AB=8 cm,
所以A2B2=AH=AB·cos 30°=8× =4 (cm).
即旋转后木棒的影子A2B2的长为4 cm.
解:
小试牛刀
5 已知一纸板的形状为正方形ABCD,且边长为10 cm.
如图,四边形A1B1C1D1是正方形ABCD 在面β上的正
投影,AD,BC 与投影面β 平行,且AB,CD 与投影
面β 成30°角,求正方形ABCD 的正投影的面积.
小试牛刀
解:
规律总结:求投影的面积,先确定投影的形状,再根据相
应的面积公式,有针对性地求出相关线段的长.
过点A 作AH⊥BB1于点H. 依题意,得∠BAH=30°,四边形A1B1C1D1是矩形,其中A1D1=AD,A1B1=AH.
∵AH⊥BB1,∠BAH=30°,∴AH=AB ·cos 30°=
10× =5(cm),∴A1B1=AH=5 cm.
∵A1D1=AD=10 cm,
∴S四边形A1B1C1D1=A1B1·A1D1=5 ×10=50 (cm2).
则正方形ABCD 的正投影的面积是50 cm2.
小试牛刀
一个圆锥的轴截面平行于投影面,圆锥的正投影是等腰三角形,
如图所示,等腰三角形的腰长为13 cm,高为12 cm,求该圆锥
的体积及表面积.(提示:V圆锥= πr 2h,其中r 是底面圆的半
径,h 是圆锥的高)
小试牛刀
解:
由于圆锥的轴截面平行于投影面,其正投影是等腰三角形,因此圆锥的高等于等腰三角形的高;圆锥底面圆的半径等于等腰三角形底边长的一半.如图,作AD⊥BC 于D,AB=AC=13 cm,AD=12 cm,∴CD=5 cm,
∴r=CD=5 cm,h=12 cm.
∴V圆锥= πr 2h=100π cm3,
底面周长为l=2πr=10π cm,
母线长R=AC=13 cm,
∴S表= lR+πr 2=90π cm2.
小试牛刀
7 操作与研究:
如图,△ABC 被平行光线照射,CD
⊥AB 于D,CD 与光线平行,AB 在投
影面上.
(1)指出图中AC 的投影是什么,CD 与BC 的投影呢?
(2)探究:当△ABC 为直角三角形(∠ACB=90°)时,易
得AC 2=AD ·AB,此时有如下结论:直角三角形一直
角边的平方等于它在斜边上的射影与斜边的乘积,这
一结论我们称为射影定理.
通过上述结论的推理,请证明以下两个结论:
①BC 2=BD ·AB;②CD 2=AD ·BD.
小试牛刀
(1)解:AC 的投影是AD,CD 的投影是点D,BC 的投影
是BD.
(2)证明:①易证得△BCD∽△BAC,可得BC 2=BD ·AB;
②易证得△ACD∽△CBD,可得CD 2=AD ·BD.
课堂小结
课堂小结
1.回顾正投影的含义及其性质;
2.反思作简单几何图形的正投影的过程及自己作图过程中失误的原因,体会正投影的作图方法与技巧;
3.物体的正投影的形状、大小与它相对于投影面的位置是否有关系?
课堂小结
平行投影与中心投影的区别与联系 联系 都是物体在光线的照射下,在某个平面内形成的影子,即都是投影 区 别 光线 中心投影 从一点发出的投射线
平行投影 平行的投射线
物体与投影面平行时的投影 中心投影 放大(位似变换)
平行投影 全等
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
