【班海精品】冀教版(新)九下-29.1 点与圆的位置关系 【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-29.1 点与圆的位置关系 【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览










文档简介
(共41张PPT)
29.1 点与圆的位置关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.你知道运动员的成绩是如何计算的吗?
新课精讲
探索新知
1
知识点
点与圆的位置关系的判定
思考:
足球运动员踢出的足球在球场上滚动,在足球穿越中圈区(中间圆形区域)的过程中,可将足球看成一个点,这个点与圆具有怎样的位置关系?
探索新知
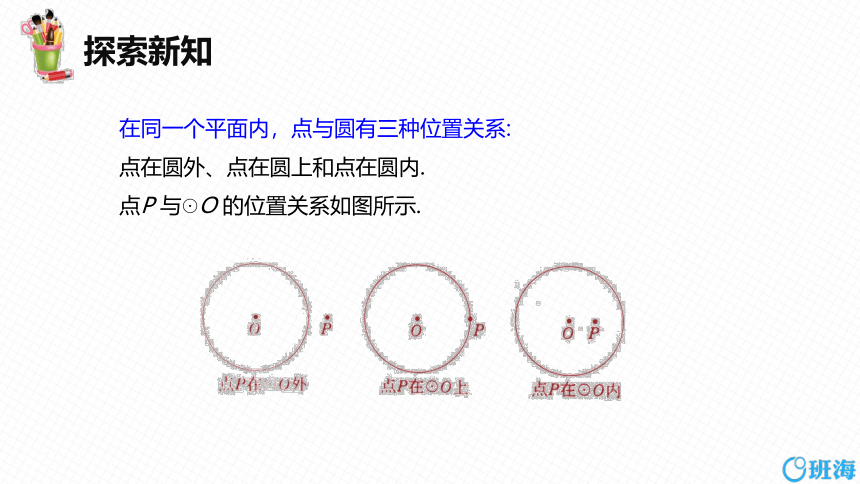
在同一个平面内,点与圆有三种位置关系:
点在圆外、点在圆上和点在圆内.
点P 与☉O 的位置关系如图所示.
探索新知
设⊙O 的半径为r,点P 到圆心的距离OP =d,则有:
点P 在圆外 d>r;
点P 在圆上 d=r;
点P 在圆内 d<r.
符号“ ”读作“等价于”,它表示从符号“ ”的左端可以推出右端,从右
端也可以推出左端.
探索新知
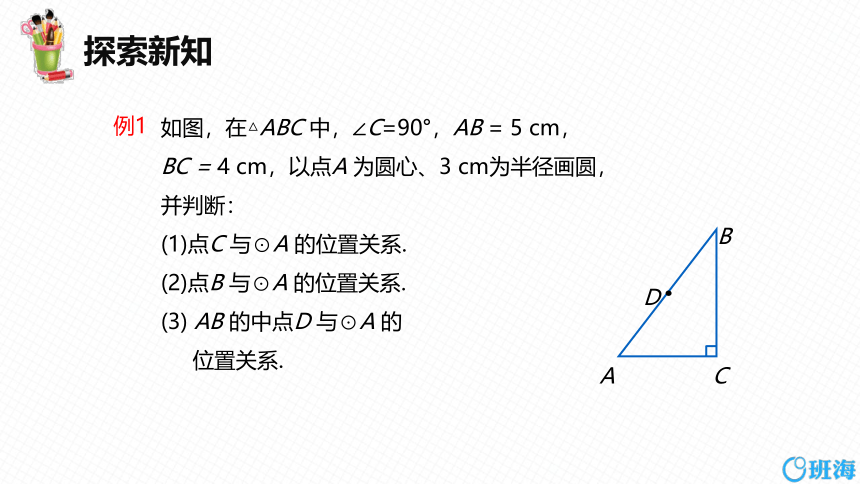
如图,在△ABC 中,∠C=90°,AB = 5 cm,
BC = 4 cm,以点A 为圆心、3 cm为半径画圆,
并判断:
(1)点C 与⊙A 的位置关系.
(2)点B 与⊙A 的位置关系.
(3) AB 的中点D 与⊙A 的
位置关系.
例1
B
A
D
C
.
探索新知
解:
已知⊙A 的半径r = 3 cm.
(1)因为
所以点C 在⊙A上
(2)因为 AB =5cm>3 cm=r,所以点B 在⊙A外.
(3)因为 DA= AB=2. 5 cm<3 cm=r,
所以点 D 在⊙A 内.
探索新知
例2 已知⊙O 的半径r=5 cm,圆心O 到直线l 的距离d=
OD=3 cm,在直线l上有P,Q,R 三点,且有PD=
4 cm,QD=5 cm,RD=3 cm,那么P,Q,R 三
点与⊙O 的位置关系各是怎样的?
要判断点和圆的位置关系,实质上是要比较点到圆
心的距离与半径的大小,而半径为已知量,即需求
出相关点到圆心的距离.
导引:
探索新知
解:如图,连接OR,OP,OQ.
∵PD=4 cm,OD=3 cm,且OD⊥l,
∴点P 在⊙O 上;
∵QD=5 cm,
∴点Q 在⊙O 外;
∵RD=3 cm,
∴点R 在⊙O 内.
探索新知
总 结
判断点和圆的位置关系,关键是计算出点到圆心的距离,再与圆的半径比较大小,由数量关系决定位置关系;构造直角三角形并运用勾股定理是求距离的常用辅助方法.
典题精讲
在直角坐标系中,以原点为圆心的⊙O 的半径为5 .判断以下各点与⊙O 的位置关系:
A(4, 2),B(-3, 4),C(4,-4),D(1,5).
1
解:
已知⊙O 的半径r=5,过点A 向x 轴作垂线,交x 轴于点M,连接OA,易得OM=4,AM=2,
所以
所以点A 在⊙O 内.
同理可得,OB=5=r,所以点B 在⊙O上.
OC= >5=r,所以点C 在⊙O 外.
OD= >5=r,所以点D 在⊙O 外.
典题精讲
⊙O 的半径为5 cm,点A 到圆心O 的距离OA=3 cm,则点A 与⊙O 的位置关系为( )
A.点A 在圆上 B.点A 在圆内
C.点A 在圆外 D.无法确定
2
B
若⊙O 的面积为25π,在同一平面内有一个点P,且点P 到圆心O 的距离为4.9,则点P 与⊙O 的位置关系是( )
A.点P 在⊙O 外 B.点P 在⊙O 上
C.点P 在⊙O 内 D.无法确定
3
C
典题精讲
在公园的O 处附近有E,F,G,H 四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O 为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H 四棵树中需要被移除的为( )
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
4
A
探索新知
如图所示 .∵点B 在⊙A内部,
∴|a-1|<2.
∴-1<a<3.
导引:
例3
若点B (a,0)在以点A (1,0)为圆心,2为半径的圆内,则a 的取值范围为( )
A.-1<a<3
B.a<3
C.a>-1
D.a>3或a<-1
A
2
知识点
点与圆的位置关系的性质
探索新知
总 结
解答本题运用了转化思想,关键是将条件转化成点到圆心的距离与圆的半径之间的大小关系,即列出方程或不等式来解答.
探索新知
例4
如图,铁路MN 和公路PQ 在点O 处交汇,∠QON=30°,公路PQ 上A 处距离O 点240米,如果火车行驶时,周围200米以内会受到噪音的影响,那么火车在铁路MN 上沿MN 方向以72千米/时的速度行驶时,A 处受到噪音影响的时间是多长?
探索新知
过点A 作AC⊥ON 于C,求出AC 的长,以点A为圆心,200米为半径作圆,与MN 交于点B,D,则当火车到B 点时开始对A 处产生噪音影响,直到火车到D 点时噪音才消失.
导引:
如图,过点A 作AC⊥ON 于C,以点A 为圆心,200米为半径作圆,与MN 交于点B,D,连接AB,AD,则AB=AD=200米.
解:
探索新知
∵∠QON=30°,OA=240米,
∴AC=120米.
当火车到B 点时对A 处产生噪音影响,
∵AB=200米,AC=120米,
∴由勾股定理得BC=160米,同理可得CD=160米,
∴BD=320米.
∵72千米/时=20米/秒,
∴A 处受到噪音影响的时间应是320÷20=16(秒).
探索新知
总 结
本题考查的是点与圆的位置关系,根据火车行驶的方向,速度,以及它在以A为圆心,200米为半径的圆内行驶的弦BD的长,求出A处受到噪音影响的时间.
典题精讲
如图,某海域以点A 为圆心、3 km为半径的圆形区域为多暗礁的危险区,但渔业资源丰富. 渔船要从点B 处前往点A 处进行捕鱼,B,A两点之间的距离是10 km.如果渔船始终保持10 km/h的航速行驶,那么在什么时段内,渔船是安全的?渔船何时进入危险区域?
1
典题精讲
渔船在圆形区域外是安全的,
=0.7(h),0.7 h=42 min,
所以渔船从点B 出发,在42 min以内是安全的,从42 min后进入危险区域.
解:
典题精讲
已知点A 在半径为r 的⊙O 内,点A 与点O 的距离为6,则r的取值范围是( )
A.r >6 B.r ≥6 C.r <6 D.r ≤6
2
A
已知矩形ABCD 的边AB=6,AD=8,如果以点A 为圆心作⊙A,使B,C,D 三点中在圆内和圆外都至少有一个点,那么⊙A 的半径r 的取值范围是( )
A.63
A
典题精讲
采石厂工人爆破时,为了安全,点燃炸药导火线后,要在炸药爆炸前转移到400 m以外的安全区域,导火线燃烧的速度是1 cm/s,工人离开的速度是5 m/s,至少需要导火线的长度是( )
A.70 cm B.75 cm
C.79 cm D.80 cm
4
D
易错提醒
若⊙O 所在平面内一点P 到⊙O上的点的最大距离为a,最小距离为b (a>b),则此圆的半径为( )
A. B.
C. 或 D.a+b 或 a-b
C
易错点:考虑问题不全面而致错.
学以致用
小试牛刀
在平面直角坐标系中,⊙P、⊙Q 的位置如图所示,下列四个点中,在⊙P 外部且在⊙Q 内部的是( )
A.(1,2)
B.(2,1)
C.(2,-1)
D.(3,1)
1
C
小试牛刀
如图所示,在Rt△ABC 中,∠C=90°,AC=4,BC=3,点D 是AB 的中点,以B 为圆心,BC 的长为半径作⊙B,则点D 和⊙B 的位置关系是( )
A.点D 在⊙B 内
B.点D 在⊙B 上
C.点D 在⊙B 外
D.不能确定
2
A
小试牛刀
如图,王大伯家屋后有一块长12 m,宽8 m的矩形空地,他在以长BC 为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.3 m
B.5 m
C.7 m
D.9 m
3
A
小试牛刀
4 如图所示,已知△ABC 中,∠C=90°,AC=6,
BC=8,以点C 为圆心作⊙C,半径为r.
(1)当r 取什么值时,点A,B 在⊙C 外?
(2)当r 取什么值时,点A 在⊙C 内,点B 在⊙C 外?
解:(1)若点A,B 在⊙C 外,
则有AC>r. ∵AC=6,∴r<6.
(2)若点A 在⊙C 内,点B 在⊙C 外,
则有AC<r<BC,
∵AC=6,BC=8,∴6<r<8.
小试牛刀
5 如图所示,AD 为△ABC 外接圆的直径,AD⊥BC,垂
足为点F,∠ABC 的平分线交AD 于点E,连接BD,CD.
(1)求证:BD=CD;
(2)判断B,E,C 三点是否在以D 为圆心,
DB 为半径的圆上,并说明理由.
(1)证明:∵AD 为圆的直径,AD⊥BC,∴根据垂径定理可
知BF=CF,在△AFB 和△AFC 中,AF=AF,∠AFB
=∠AFC=90°,BF=CF,∴△AFB ≌ △AFC,
∴∠BAD=∠CAD,∴ ,∴BD=CD.
小试牛刀
(2)解:B,E,C 三点在以D 为圆心,DB 为半径的圆上.
理由如下:由(1)知 ,
∴∠BAD=∠CBD.
∵BE 是∠ABC 的平分线,
∴∠CBE=∠ABE,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+
∠ABE,∴∠DBE=∠DEB.
∴DB=DE.
由(1)知BD=CD,∴DB=DE=DC.
∴B,E,C 三点在以D 为圆心,DB 为半径的圆上.
小试牛刀
如图①,若∠ACB=∠ADB=90°,则点D 在经过A,B,C三点的圆上.如图②,如果∠ACB=∠ADB=α (α<90°),点C,D 在AB 的同侧.求证:点D 在经过A,B,C 三点的圆上.
证明:假设点D 不在经过A,B,C 三点的圆上,则点D
在经过A,B,C 三点的圆外或圆内.设经过A,
B,C 三点的圆为⊙O.
小试牛刀
①当点D 在⊙O 内时,如图①.
设AD 的延长线交⊙O 于点E,连接BE,则∠ACB=∠AEB.
∵∠ADB=∠AEB+∠EBD,∴∠ADB>
∠AEB,即∠ADB>∠ACB,这与∠ACB
=∠ADB 矛盾,∴点D 不在⊙O 内.
②当点D 在⊙O 外时,如图②.
设AD 交⊙O 于点E,连接BE,则∠ACB=∠AEB.
∵∠AEB=∠D+∠EBD,∴∠D<∠AEB,即∠D<∠ACB,
这与∠D=∠ACB 矛盾,∴点D 不在⊙O 外.
综上可知,点D 不在⊙O 内,也不在⊙O 外.
∴点D 在⊙O上,即点D 在经过A,B,C 三点的圆上.
小试牛刀
某学校的教室A 的东240米的O 点处有一货场,经过O 点沿北偏东60°方向有一条公路,假定运货车形成的噪音影响的范围在130米以内.
(1)这条公路上的运货车产生的噪音会对学校造成影响吗?请说明理由.
(2)若运货车产生的噪音会对学校造成影响,为消除噪音,计划在公路边
修筑一段消音墙,请你计算
消音墙的长度.(只考虑
声音的直线传播)
小试牛刀
解:(1)会造成影响,理由如下:
如图,过点A 作AH⊥BC 于H,可知∠AOH=30°,
在Rt△AOH 中,AO=240米.∴AH=AO=120米.∵120米
<130米,∴点A 在以点H 为圆心,以130米长为半径的⊙H
内,即这条公路上的运货车产生的噪音会对学校造成影响.
(2)当运货车距A点130米时,学校开始受到噪音影响,假设
运货车行驶到C 处,学校开始受影响,运货车离开B 处,学
校不再受影响,则AB=AC=130米,如图,
在△ABC 中,AB=AC,AH⊥BC,∴BH=CH.
在Rt△ACH 中,AC=130米,AH=120米.
∴CH= =50(米).
∴BC=2CH=100米,即消音墙的长度为100米.
课堂小结
课堂小结
点和圆的三种位置关系:
设⊙O 的半径为r,点P 到圆心的距离为d,则
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.1 点与圆的位置关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.你知道运动员的成绩是如何计算的吗?
新课精讲
探索新知
1
知识点
点与圆的位置关系的判定
思考:
足球运动员踢出的足球在球场上滚动,在足球穿越中圈区(中间圆形区域)的过程中,可将足球看成一个点,这个点与圆具有怎样的位置关系?
探索新知
在同一个平面内,点与圆有三种位置关系:
点在圆外、点在圆上和点在圆内.
点P 与☉O 的位置关系如图所示.
探索新知
设⊙O 的半径为r,点P 到圆心的距离OP =d,则有:
点P 在圆外 d>r;
点P 在圆上 d=r;
点P 在圆内 d<r.
符号“ ”读作“等价于”,它表示从符号“ ”的左端可以推出右端,从右
端也可以推出左端.
探索新知
如图,在△ABC 中,∠C=90°,AB = 5 cm,
BC = 4 cm,以点A 为圆心、3 cm为半径画圆,
并判断:
(1)点C 与⊙A 的位置关系.
(2)点B 与⊙A 的位置关系.
(3) AB 的中点D 与⊙A 的
位置关系.
例1
B
A
D
C
.
探索新知
解:
已知⊙A 的半径r = 3 cm.
(1)因为
所以点C 在⊙A上
(2)因为 AB =5cm>3 cm=r,所以点B 在⊙A外.
(3)因为 DA= AB=2. 5 cm<3 cm=r,
所以点 D 在⊙A 内.
探索新知
例2 已知⊙O 的半径r=5 cm,圆心O 到直线l 的距离d=
OD=3 cm,在直线l上有P,Q,R 三点,且有PD=
4 cm,QD=5 cm,RD=3 cm,那么P,Q,R 三
点与⊙O 的位置关系各是怎样的?
要判断点和圆的位置关系,实质上是要比较点到圆
心的距离与半径的大小,而半径为已知量,即需求
出相关点到圆心的距离.
导引:
探索新知
解:如图,连接OR,OP,OQ.
∵PD=4 cm,OD=3 cm,且OD⊥l,
∴点P 在⊙O 上;
∵QD=5 cm,
∴点Q 在⊙O 外;
∵RD=3 cm,
∴点R 在⊙O 内.
探索新知
总 结
判断点和圆的位置关系,关键是计算出点到圆心的距离,再与圆的半径比较大小,由数量关系决定位置关系;构造直角三角形并运用勾股定理是求距离的常用辅助方法.
典题精讲
在直角坐标系中,以原点为圆心的⊙O 的半径为5 .判断以下各点与⊙O 的位置关系:
A(4, 2),B(-3, 4),C(4,-4),D(1,5).
1
解:
已知⊙O 的半径r=5,过点A 向x 轴作垂线,交x 轴于点M,连接OA,易得OM=4,AM=2,
所以
所以点A 在⊙O 内.
同理可得,OB=5=r,所以点B 在⊙O上.
OC= >5=r,所以点C 在⊙O 外.
OD= >5=r,所以点D 在⊙O 外.
典题精讲
⊙O 的半径为5 cm,点A 到圆心O 的距离OA=3 cm,则点A 与⊙O 的位置关系为( )
A.点A 在圆上 B.点A 在圆内
C.点A 在圆外 D.无法确定
2
B
若⊙O 的面积为25π,在同一平面内有一个点P,且点P 到圆心O 的距离为4.9,则点P 与⊙O 的位置关系是( )
A.点P 在⊙O 外 B.点P 在⊙O 上
C.点P 在⊙O 内 D.无法确定
3
C
典题精讲
在公园的O 处附近有E,F,G,H 四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O 为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H 四棵树中需要被移除的为( )
A.E,F,G
B.F,G,H
C.G,H,E
D.H,E,F
4
A
探索新知
如图所示 .∵点B 在⊙A内部,
∴|a-1|<2.
∴-1<a<3.
导引:
例3
若点B (a,0)在以点A (1,0)为圆心,2为半径的圆内,则a 的取值范围为( )
A.-1<a<3
B.a<3
C.a>-1
D.a>3或a<-1
A
2
知识点
点与圆的位置关系的性质
探索新知
总 结
解答本题运用了转化思想,关键是将条件转化成点到圆心的距离与圆的半径之间的大小关系,即列出方程或不等式来解答.
探索新知
例4
如图,铁路MN 和公路PQ 在点O 处交汇,∠QON=30°,公路PQ 上A 处距离O 点240米,如果火车行驶时,周围200米以内会受到噪音的影响,那么火车在铁路MN 上沿MN 方向以72千米/时的速度行驶时,A 处受到噪音影响的时间是多长?
探索新知
过点A 作AC⊥ON 于C,求出AC 的长,以点A为圆心,200米为半径作圆,与MN 交于点B,D,则当火车到B 点时开始对A 处产生噪音影响,直到火车到D 点时噪音才消失.
导引:
如图,过点A 作AC⊥ON 于C,以点A 为圆心,200米为半径作圆,与MN 交于点B,D,连接AB,AD,则AB=AD=200米.
解:
探索新知
∵∠QON=30°,OA=240米,
∴AC=120米.
当火车到B 点时对A 处产生噪音影响,
∵AB=200米,AC=120米,
∴由勾股定理得BC=160米,同理可得CD=160米,
∴BD=320米.
∵72千米/时=20米/秒,
∴A 处受到噪音影响的时间应是320÷20=16(秒).
探索新知
总 结
本题考查的是点与圆的位置关系,根据火车行驶的方向,速度,以及它在以A为圆心,200米为半径的圆内行驶的弦BD的长,求出A处受到噪音影响的时间.
典题精讲
如图,某海域以点A 为圆心、3 km为半径的圆形区域为多暗礁的危险区,但渔业资源丰富. 渔船要从点B 处前往点A 处进行捕鱼,B,A两点之间的距离是10 km.如果渔船始终保持10 km/h的航速行驶,那么在什么时段内,渔船是安全的?渔船何时进入危险区域?
1
典题精讲
渔船在圆形区域外是安全的,
=0.7(h),0.7 h=42 min,
所以渔船从点B 出发,在42 min以内是安全的,从42 min后进入危险区域.
解:
典题精讲
已知点A 在半径为r 的⊙O 内,点A 与点O 的距离为6,则r的取值范围是( )
A.r >6 B.r ≥6 C.r <6 D.r ≤6
2
A
已知矩形ABCD 的边AB=6,AD=8,如果以点A 为圆心作⊙A,使B,C,D 三点中在圆内和圆外都至少有一个点,那么⊙A 的半径r 的取值范围是( )
A.6
A
典题精讲
采石厂工人爆破时,为了安全,点燃炸药导火线后,要在炸药爆炸前转移到400 m以外的安全区域,导火线燃烧的速度是1 cm/s,工人离开的速度是5 m/s,至少需要导火线的长度是( )
A.70 cm B.75 cm
C.79 cm D.80 cm
4
D
易错提醒
若⊙O 所在平面内一点P 到⊙O上的点的最大距离为a,最小距离为b (a>b),则此圆的半径为( )
A. B.
C. 或 D.a+b 或 a-b
C
易错点:考虑问题不全面而致错.
学以致用
小试牛刀
在平面直角坐标系中,⊙P、⊙Q 的位置如图所示,下列四个点中,在⊙P 外部且在⊙Q 内部的是( )
A.(1,2)
B.(2,1)
C.(2,-1)
D.(3,1)
1
C
小试牛刀
如图所示,在Rt△ABC 中,∠C=90°,AC=4,BC=3,点D 是AB 的中点,以B 为圆心,BC 的长为半径作⊙B,则点D 和⊙B 的位置关系是( )
A.点D 在⊙B 内
B.点D 在⊙B 上
C.点D 在⊙B 外
D.不能确定
2
A
小试牛刀
如图,王大伯家屋后有一块长12 m,宽8 m的矩形空地,他在以长BC 为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.3 m
B.5 m
C.7 m
D.9 m
3
A
小试牛刀
4 如图所示,已知△ABC 中,∠C=90°,AC=6,
BC=8,以点C 为圆心作⊙C,半径为r.
(1)当r 取什么值时,点A,B 在⊙C 外?
(2)当r 取什么值时,点A 在⊙C 内,点B 在⊙C 外?
解:(1)若点A,B 在⊙C 外,
则有AC>r. ∵AC=6,∴r<6.
(2)若点A 在⊙C 内,点B 在⊙C 外,
则有AC<r<BC,
∵AC=6,BC=8,∴6<r<8.
小试牛刀
5 如图所示,AD 为△ABC 外接圆的直径,AD⊥BC,垂
足为点F,∠ABC 的平分线交AD 于点E,连接BD,CD.
(1)求证:BD=CD;
(2)判断B,E,C 三点是否在以D 为圆心,
DB 为半径的圆上,并说明理由.
(1)证明:∵AD 为圆的直径,AD⊥BC,∴根据垂径定理可
知BF=CF,在△AFB 和△AFC 中,AF=AF,∠AFB
=∠AFC=90°,BF=CF,∴△AFB ≌ △AFC,
∴∠BAD=∠CAD,∴ ,∴BD=CD.
小试牛刀
(2)解:B,E,C 三点在以D 为圆心,DB 为半径的圆上.
理由如下:由(1)知 ,
∴∠BAD=∠CBD.
∵BE 是∠ABC 的平分线,
∴∠CBE=∠ABE,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+
∠ABE,∴∠DBE=∠DEB.
∴DB=DE.
由(1)知BD=CD,∴DB=DE=DC.
∴B,E,C 三点在以D 为圆心,DB 为半径的圆上.
小试牛刀
如图①,若∠ACB=∠ADB=90°,则点D 在经过A,B,C三点的圆上.如图②,如果∠ACB=∠ADB=α (α<90°),点C,D 在AB 的同侧.求证:点D 在经过A,B,C 三点的圆上.
证明:假设点D 不在经过A,B,C 三点的圆上,则点D
在经过A,B,C 三点的圆外或圆内.设经过A,
B,C 三点的圆为⊙O.
小试牛刀
①当点D 在⊙O 内时,如图①.
设AD 的延长线交⊙O 于点E,连接BE,则∠ACB=∠AEB.
∵∠ADB=∠AEB+∠EBD,∴∠ADB>
∠AEB,即∠ADB>∠ACB,这与∠ACB
=∠ADB 矛盾,∴点D 不在⊙O 内.
②当点D 在⊙O 外时,如图②.
设AD 交⊙O 于点E,连接BE,则∠ACB=∠AEB.
∵∠AEB=∠D+∠EBD,∴∠D<∠AEB,即∠D<∠ACB,
这与∠D=∠ACB 矛盾,∴点D 不在⊙O 外.
综上可知,点D 不在⊙O 内,也不在⊙O 外.
∴点D 在⊙O上,即点D 在经过A,B,C 三点的圆上.
小试牛刀
某学校的教室A 的东240米的O 点处有一货场,经过O 点沿北偏东60°方向有一条公路,假定运货车形成的噪音影响的范围在130米以内.
(1)这条公路上的运货车产生的噪音会对学校造成影响吗?请说明理由.
(2)若运货车产生的噪音会对学校造成影响,为消除噪音,计划在公路边
修筑一段消音墙,请你计算
消音墙的长度.(只考虑
声音的直线传播)
小试牛刀
解:(1)会造成影响,理由如下:
如图,过点A 作AH⊥BC 于H,可知∠AOH=30°,
在Rt△AOH 中,AO=240米.∴AH=AO=120米.∵120米
<130米,∴点A 在以点H 为圆心,以130米长为半径的⊙H
内,即这条公路上的运货车产生的噪音会对学校造成影响.
(2)当运货车距A点130米时,学校开始受到噪音影响,假设
运货车行驶到C 处,学校开始受影响,运货车离开B 处,学
校不再受影响,则AB=AC=130米,如图,
在△ABC 中,AB=AC,AH⊥BC,∴BH=CH.
在Rt△ACH 中,AC=130米,AH=120米.
∴CH= =50(米).
∴BC=2CH=100米,即消音墙的长度为100米.
课堂小结
课堂小结
点和圆的三种位置关系:
设⊙O 的半径为r,点P 到圆心的距离为d,则
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
