【班海精品】冀教版(新)九下-29.2 直线与圆的位置关系【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-29.2 直线与圆的位置关系【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
29.2 直线与圆的位置关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
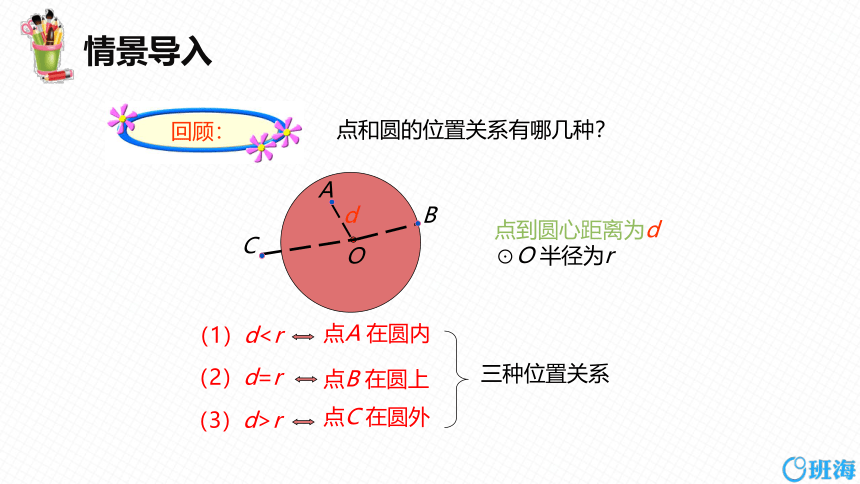
情景导入
点和圆的位置关系有哪几种?
(1)d(2)d=r
(3)d>r
A
B
C
d
点A 在圆内
点B 在圆上
点C 在圆外
三种位置关系
O
点到圆心距离为d
⊙O 半径为r
回顾:
新课精讲
探索新知
1
知识点
直线与圆的位置关系与直线与圆的公共点个数间的关系
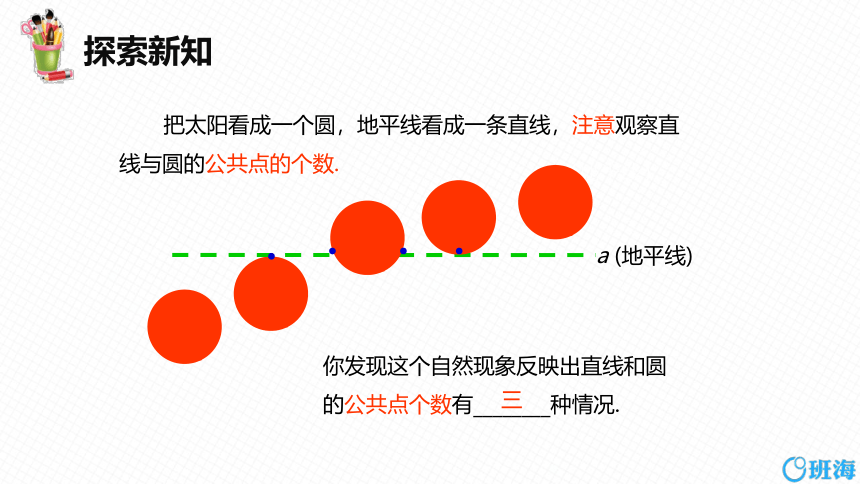
清晨,一轮红日从东方冉冉升起,太阳的轮廓就像一个运动的圆,从地平线下渐渐升到空中.在此过程中,太阳轮廓与地平线有几种不同的位置关系呢
你发现这个自然现象反映出直线和圆
的公共点个数有________种情况.
探索新知
●O
●O
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数.
a(地平线)
a (地平线)
●O
●O
●O
三
●
●
●
●
探索新知
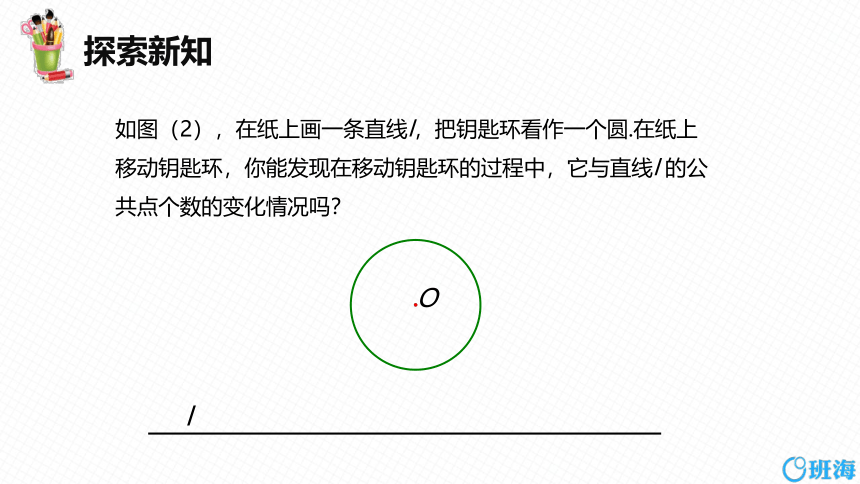
如图(2),在纸上画一条直线l,把钥匙环看作一个圆.在纸上
移动钥匙环,你能发现在移动钥匙环的过程中,它与直线l 的公
共点个数的变化情况吗?
l
O
探索新知
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.
直线和圆没有公共点,这时我们就说这条直线和圆相离.
探索新知
例1 若直线l 与⊙O 有公共交点,则直线l 与⊙O 的位置关
系是( )
A.相交 B.相切
C.相离 D.相切或相交
直线l 与⊙O 有公共交点有两种情况:(1)有惟一公共交点,此时直线l 与⊙O 相切;(2)有两个交点,此时直线l 与⊙O 相交,故应选D.
D
导引:
典题精讲
若直线m 与⊙O 的公共点个数不小于1,则直线m 与⊙O 的位置关系是( )
A.相交 B.相切
C.相交或相切 D.相离
1
C
典题精讲
下列命题:
①如果一条直线与圆没有公共点,那么这条直线与圆相离;
②如果一条射线与圆没有公共点,那么这条射线所在的直线与圆相离;
③如果一条线段与圆没有公共点,那么这条线段所在的直线与圆相离.其中为真命题的是( )
A.① B.②
C.③ D.①②③
2
A
探索新知
2
知识点
直线与圆的位置关系的判定
思考:
设⊙O 的半径为r,圆心O 到直线l 的距离为d,在直线和圆的不同位置关系中,你能根据d 与r 的大小关系确定直线和圆的位置关系吗?
探索新知
如图,圆心O 到直线的距离d 与⊙O 的半径r 的大小有什么关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
1)直线和圆相交
d______r;
2)直线和圆相切
3)直线和圆相离
<
d______r;
=
d______r;
>
探索新知
如图,在 Rt△ABC 中,∠C= 90°,AC= 3 cm,BC= 4 cm. 以点C为圆心,2cm,2.4cm,3cm分别为半径画⊙C,斜边AB 分别与⊙C 有怎样的位置关系?为什么?
例2
B
A
C
探索新知
如图,过点C 作CD丄AB,垂足为D. 在 Rt△ABC 中,
由三角形的面积公式,并整理,得
AC BC=AB CD.
从而
即圆心C 到斜边AB 的距离d=2.4 cm.
当r=2cm时,d>r,斜边AB 与⊙C 相离.
当r=2.4cm时,d=r,斜边AB 与⊙C 相切.
当r=3cm时,d<r,斜边AB 与⊙C 相交.
解:
典题精讲
已知一个圆的直径为10. 如果这个圆的圆心到一条直线的距离分别等于3,5,6,那么这条直线与这个圆的位置关系分别是怎样的?
1
因为圆的直径为10,所以圆的半径为5.当直线与圆心的距离等于3时,因为3<5,所以直线与圆相交;
当直线与圆心的距离等于5时,因为5=5,所以直线与圆相切;
当直线与圆心的距离等于6时,因为6>5,所以直线与圆相离.
解:
典题精讲
如图,∠AOB=30°,M 为 OB 上一点,且 OM= 6 cm. 以点M 为圆心画圆,当其半径r 分别等于2cm,3cm,4cm时,直线OA 与⊙M 分别有怎样的位置关系?为什么?
2
o
B
A
M
.
典题精讲
过点M 作OA 的垂线,垂足为N.
因为∠AOB=30°,∠ONM=90°,OM=6 cm,所以MN=12OM=3 cm.
当r=2 cm时,MN>r,所以⊙M 与直线OA 相离;当r=3 cm时,MN=r,所以⊙M 与直线OA 相切;当r=4 cm时,MN<r,所以⊙M 与直线OA 相交.
解:
典题精讲
在Rt △ABC 中,∠C=90°,BC=3 cm,AC=4 cm,以点C 为圆心,以2.5 cm为半径画圆,则⊙C 与直线AB 的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
3
A
已知⊙O 的半径为3,M 为直线AB上一点,若MO=3,则直线AB 与⊙O 的位置关系为( )
A.相切 B.相交
C.相切或相离 D.相切或相交
4
D
探索新知
3
知识点
直线与圆的位置关系的性质
例3 在Rt△ABC 中,AC=3 cm,BC=4 cm,∠ACB=
90°.若以点C 为圆心,r 为半径的圆与直线AB 不相
离,求r 的取值范围.
⊙C 与直线AB 不相离,即⊙C 与直线AB 相交或相
切,因此只需点C 到直线AB 的距离小于或等于r.
导引:
探索新知
如图,过点C 作CD⊥AB 于点D.
在Rt△ABC 中,
AC=3 cm,BC=4 cm,∠ACB=90°,
∴AB=
又∵S△ABC= AB CD = AC BC,
∴CD=2.4 cm.
∴r ≥ 2.4 cm.
解:
探索新知
总 结
(1)直线和圆的位置关系的应用过程实质是一种数形结合思想的转化过程,它始终是“数”:圆心到直线的距离与圆的半径大小,与“形”:直线和圆的位置关系之间的相互转化.
(2)圆心到直线的距离通常用勾股定理与面积相等法求出.
典题精讲
如图,给定一个半径长为2的圆,圆心O 到水平直线l 的距离为d,即OM=d.我们把圆上到直线l 的距离等于1的点的个数记为m.如d=0时,l 为经过圆心O 的一条直线,此时圆上有四个到直线l 的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=________;
(2)当m=2时,d 的取值范围
是___________.
1
1
1<d<3
典题精讲
以坐标原点O 为圆心,作半径为2的圆,若直线 y=-x+b与⊙O 相交,则b 的取值范围是( )
A.0≤b<2
B.-2 ≤b≤2
C.-2 <b<2
D.-2 <b<2
2
D
典题精讲
如图所示,在平面直角坐标系x O y中,半径为2的⊙P 的圆心P 的坐标为(-3,0),将⊙P 沿x 轴正方向平移,使⊙P 与y 轴相切,则平移的距离为( )
A.1
B.1或5
C.3
D.5
3
B
易错提醒
如图,在平面直角坐标系第一象限内有一矩形OABC,B (4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心P 的坐标为__________________________________.
易错点:判断圆和各边相切时考虑不全而漏解.
(1,1)或(3,1)或(2,0)或(2,2)
学以致用
小试牛刀
如图,在△ABC 中,AB=6,AC=8,BC=10,D,E 分别是AC,AB 的中点,则以DE 为直径的圆与BC 的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
1
A
小试牛刀
如图,在△ABC 中,AB=10,AC=8,BC=6,以边AB 的中点O 为圆心,作半圆与AC 相切,点P,Q 分别是边BC 和半圆上的动点,连接PQ,则PQ 长的最大值与最小值的和是( )
A.6
B.
C.9
D.
2
C
小试牛刀
如图,在直角坐标系中,⊙O 的半径为1,则直线 y=-x+ 与⊙O 的位置关系是( )
A.相离
B.相交
C.相切
D.以上三种情形都有可能
3
C
小试牛刀
4 如图,在Rt△ABC中,∠BAC=90°.
(1)先作∠ACB 的平分线交AB 边于点P,再以点P 为圆心,PA长为半
径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断BC 与(1)中⊙P 的位置
关系,并证明你的结论.
解:(1)如图所示,⊙P 为所求的圆.
(2)BC 与⊙P 相切.理由:
如图,过P 作PD⊥BC,交BC 于点D.
∵CP 为∠ACB 的平分线,且PA⊥AC,PD⊥CB,∴PD=PA.
∴点P 到BC 的距离等于⊙P 的半径.∴BC 与⊙P 相切.
小试牛刀
如图,在△ABC 中,∠C=90°,∠BAC 的平分线交BC 于点D,
点O 在AB上,以点O 为圆心,OA 为半径的圆恰好经过点D,
分别交AC,AB 于点E,F.
(1)试判断直线BC 与⊙O 的位置关系,并说明理由;
(2)若BD=2 ,BF=2,求阴影部分的面积(结果保留π).
解:(1)BC 与⊙O 相切.
理由:如图,连接OD.
∵AD 是∠BAC 的平分线,
∴∠BAD=∠CAD. ∵OD=OA,
∴∠OAD=∠ODA. ∴∠CAD=∠ODA. ∴OD∥AC.
∴∠ODB=∠C=90°,
小试牛刀
即圆心O 到BC 的距离等于OD 的长度.
又∵OD 为半径,∴BC 与⊙O 相切.
(2)设OF=OD=x,则OB=OF+BF=x+2,
根据勾股定理得OB 2=OD 2+BD 2,
即(x+2)2=x 2+12.解得x=2,即OD=OF=2.
∴OB=2+2=4.
∵在Rt△ODB 中,OD= OB,∴∠B=30°.
∴∠DOB=60°. ∴S扇形ODF = ×π×22= .
则阴影部分的面积为S△ODB-S扇形ODF= ×2×2 -
=2 - .故阴影部分的面积为2 - .
小试牛刀
解:如图,过点P 作PC⊥OB,垂足为C,
则∠OCP=90°,∵∠AOB=30°,
∴PC= OP=12 cm.
(1)当r=12 cm时,r=PC,
∴⊙P 与OB 相切.
(2)当⊙P 与OB 相离时,r<PC,
∴r 需满足的条件是0 cm<r<12 cm.
如图,已知∠AOB=30°,P 是OA上的一点,OP=24cm,以r 为半径作⊙P.
(1)若r=12 cm,试判断⊙P 与射线OB 的位置关系;
(2)若⊙P 与OB 相离,试求出r 需满足的条件.
小试牛刀
7 如图,在Rt△ABC 中,∠C=90°,BE 平分∠ABC 交AC 于
点E,点D 在线段AB 上,DE⊥BE 于点E .
(1)判断直线AC 与△DBE 的外接圆的位
置关系,并证明你的结论;
(2)若AD=6,AE=6 ,求BC 的长.
解:(1)直线AC 与△DBE 的外接圆相切.
证明:∵DE⊥BE 于点E,
∴BD为 △DBE 的外接圆的直径,如图,设圆心为O,连接
OE,得OE=OB.∴∠OBE=∠OEB.
∵BE 平分∠ABC,∴∠CBE=∠OBE.
∴∠OEB=∠CBE.∴BC∥OE.
又∵∠C=90°,∴∠OEC=90°.
∴点O 到直线AC 的距离等于OE 的长.
小试牛刀
又∵OE 为△DBE 的外接圆的半径,
∴O 到直线AC 的距离等于半径.
∴直线AC 与△DBE 的外接圆相切.
(2)设OE=OD=x,在Rt△AEO 中,
AO 2=AE 2+EO 2,即(6+x)2=(6 )2+x 2,解得x=3.
∴OB=OE=OD=3,
∴AB=12,AO=9.
易证△ABC∽△AOE,
∴ ,即 ,
∴BC=4.
课堂小结
课堂小结
1.直线和圆的位置关系:相交、相切、相离.
(1)从公共点数来判断;
(2)从d 与r 间的数量关系来判断.
2.直线和圆的位置关系的性质与判定:
(1)直线和圆相离 d>r;
(2)直线和圆相切 d=r;
(3)直线和圆相交 d<r.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.2 直线与圆的位置关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
点和圆的位置关系有哪几种?
(1)d
(3)d>r
A
B
C
d
点A 在圆内
点B 在圆上
点C 在圆外
三种位置关系
O
点到圆心距离为d
⊙O 半径为r
回顾:
新课精讲
探索新知
1
知识点
直线与圆的位置关系与直线与圆的公共点个数间的关系
清晨,一轮红日从东方冉冉升起,太阳的轮廓就像一个运动的圆,从地平线下渐渐升到空中.在此过程中,太阳轮廓与地平线有几种不同的位置关系呢
你发现这个自然现象反映出直线和圆
的公共点个数有________种情况.
探索新知
●O
●O
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数.
a(地平线)
a (地平线)
●O
●O
●O
三
●
●
●
●
探索新知
如图(2),在纸上画一条直线l,把钥匙环看作一个圆.在纸上
移动钥匙环,你能发现在移动钥匙环的过程中,它与直线l 的公
共点个数的变化情况吗?
l
O
探索新知
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线.
直线和圆没有公共点,这时我们就说这条直线和圆相离.
探索新知
例1 若直线l 与⊙O 有公共交点,则直线l 与⊙O 的位置关
系是( )
A.相交 B.相切
C.相离 D.相切或相交
直线l 与⊙O 有公共交点有两种情况:(1)有惟一公共交点,此时直线l 与⊙O 相切;(2)有两个交点,此时直线l 与⊙O 相交,故应选D.
D
导引:
典题精讲
若直线m 与⊙O 的公共点个数不小于1,则直线m 与⊙O 的位置关系是( )
A.相交 B.相切
C.相交或相切 D.相离
1
C
典题精讲
下列命题:
①如果一条直线与圆没有公共点,那么这条直线与圆相离;
②如果一条射线与圆没有公共点,那么这条射线所在的直线与圆相离;
③如果一条线段与圆没有公共点,那么这条线段所在的直线与圆相离.其中为真命题的是( )
A.① B.②
C.③ D.①②③
2
A
探索新知
2
知识点
直线与圆的位置关系的判定
思考:
设⊙O 的半径为r,圆心O 到直线l 的距离为d,在直线和圆的不同位置关系中,你能根据d 与r 的大小关系确定直线和圆的位置关系吗?
探索新知
如图,圆心O 到直线的距离d 与⊙O 的半径r 的大小有什么关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
1)直线和圆相交
d______r;
2)直线和圆相切
3)直线和圆相离
<
d______r;
=
d______r;
>
探索新知
如图,在 Rt△ABC 中,∠C= 90°,AC= 3 cm,BC= 4 cm. 以点C为圆心,2cm,2.4cm,3cm分别为半径画⊙C,斜边AB 分别与⊙C 有怎样的位置关系?为什么?
例2
B
A
C
探索新知
如图,过点C 作CD丄AB,垂足为D. 在 Rt△ABC 中,
由三角形的面积公式,并整理,得
AC BC=AB CD.
从而
即圆心C 到斜边AB 的距离d=2.4 cm.
当r=2cm时,d>r,斜边AB 与⊙C 相离.
当r=2.4cm时,d=r,斜边AB 与⊙C 相切.
当r=3cm时,d<r,斜边AB 与⊙C 相交.
解:
典题精讲
已知一个圆的直径为10. 如果这个圆的圆心到一条直线的距离分别等于3,5,6,那么这条直线与这个圆的位置关系分别是怎样的?
1
因为圆的直径为10,所以圆的半径为5.当直线与圆心的距离等于3时,因为3<5,所以直线与圆相交;
当直线与圆心的距离等于5时,因为5=5,所以直线与圆相切;
当直线与圆心的距离等于6时,因为6>5,所以直线与圆相离.
解:
典题精讲
如图,∠AOB=30°,M 为 OB 上一点,且 OM= 6 cm. 以点M 为圆心画圆,当其半径r 分别等于2cm,3cm,4cm时,直线OA 与⊙M 分别有怎样的位置关系?为什么?
2
o
B
A
M
.
典题精讲
过点M 作OA 的垂线,垂足为N.
因为∠AOB=30°,∠ONM=90°,OM=6 cm,所以MN=12OM=3 cm.
当r=2 cm时,MN>r,所以⊙M 与直线OA 相离;当r=3 cm时,MN=r,所以⊙M 与直线OA 相切;当r=4 cm时,MN<r,所以⊙M 与直线OA 相交.
解:
典题精讲
在Rt △ABC 中,∠C=90°,BC=3 cm,AC=4 cm,以点C 为圆心,以2.5 cm为半径画圆,则⊙C 与直线AB 的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
3
A
已知⊙O 的半径为3,M 为直线AB上一点,若MO=3,则直线AB 与⊙O 的位置关系为( )
A.相切 B.相交
C.相切或相离 D.相切或相交
4
D
探索新知
3
知识点
直线与圆的位置关系的性质
例3 在Rt△ABC 中,AC=3 cm,BC=4 cm,∠ACB=
90°.若以点C 为圆心,r 为半径的圆与直线AB 不相
离,求r 的取值范围.
⊙C 与直线AB 不相离,即⊙C 与直线AB 相交或相
切,因此只需点C 到直线AB 的距离小于或等于r.
导引:
探索新知
如图,过点C 作CD⊥AB 于点D.
在Rt△ABC 中,
AC=3 cm,BC=4 cm,∠ACB=90°,
∴AB=
又∵S△ABC= AB CD = AC BC,
∴CD=2.4 cm.
∴r ≥ 2.4 cm.
解:
探索新知
总 结
(1)直线和圆的位置关系的应用过程实质是一种数形结合思想的转化过程,它始终是“数”:圆心到直线的距离与圆的半径大小,与“形”:直线和圆的位置关系之间的相互转化.
(2)圆心到直线的距离通常用勾股定理与面积相等法求出.
典题精讲
如图,给定一个半径长为2的圆,圆心O 到水平直线l 的距离为d,即OM=d.我们把圆上到直线l 的距离等于1的点的个数记为m.如d=0时,l 为经过圆心O 的一条直线,此时圆上有四个到直线l 的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m=________;
(2)当m=2时,d 的取值范围
是___________.
1
1
1<d<3
典题精讲
以坐标原点O 为圆心,作半径为2的圆,若直线 y=-x+b与⊙O 相交,则b 的取值范围是( )
A.0≤b<2
B.-2 ≤b≤2
C.-2 <b<2
D.-2 <b<2
2
D
典题精讲
如图所示,在平面直角坐标系x O y中,半径为2的⊙P 的圆心P 的坐标为(-3,0),将⊙P 沿x 轴正方向平移,使⊙P 与y 轴相切,则平移的距离为( )
A.1
B.1或5
C.3
D.5
3
B
易错提醒
如图,在平面直角坐标系第一象限内有一矩形OABC,B (4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心P 的坐标为__________________________________.
易错点:判断圆和各边相切时考虑不全而漏解.
(1,1)或(3,1)或(2,0)或(2,2)
学以致用
小试牛刀
如图,在△ABC 中,AB=6,AC=8,BC=10,D,E 分别是AC,AB 的中点,则以DE 为直径的圆与BC 的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
1
A
小试牛刀
如图,在△ABC 中,AB=10,AC=8,BC=6,以边AB 的中点O 为圆心,作半圆与AC 相切,点P,Q 分别是边BC 和半圆上的动点,连接PQ,则PQ 长的最大值与最小值的和是( )
A.6
B.
C.9
D.
2
C
小试牛刀
如图,在直角坐标系中,⊙O 的半径为1,则直线 y=-x+ 与⊙O 的位置关系是( )
A.相离
B.相交
C.相切
D.以上三种情形都有可能
3
C
小试牛刀
4 如图,在Rt△ABC中,∠BAC=90°.
(1)先作∠ACB 的平分线交AB 边于点P,再以点P 为圆心,PA长为半
径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断BC 与(1)中⊙P 的位置
关系,并证明你的结论.
解:(1)如图所示,⊙P 为所求的圆.
(2)BC 与⊙P 相切.理由:
如图,过P 作PD⊥BC,交BC 于点D.
∵CP 为∠ACB 的平分线,且PA⊥AC,PD⊥CB,∴PD=PA.
∴点P 到BC 的距离等于⊙P 的半径.∴BC 与⊙P 相切.
小试牛刀
如图,在△ABC 中,∠C=90°,∠BAC 的平分线交BC 于点D,
点O 在AB上,以点O 为圆心,OA 为半径的圆恰好经过点D,
分别交AC,AB 于点E,F.
(1)试判断直线BC 与⊙O 的位置关系,并说明理由;
(2)若BD=2 ,BF=2,求阴影部分的面积(结果保留π).
解:(1)BC 与⊙O 相切.
理由:如图,连接OD.
∵AD 是∠BAC 的平分线,
∴∠BAD=∠CAD. ∵OD=OA,
∴∠OAD=∠ODA. ∴∠CAD=∠ODA. ∴OD∥AC.
∴∠ODB=∠C=90°,
小试牛刀
即圆心O 到BC 的距离等于OD 的长度.
又∵OD 为半径,∴BC 与⊙O 相切.
(2)设OF=OD=x,则OB=OF+BF=x+2,
根据勾股定理得OB 2=OD 2+BD 2,
即(x+2)2=x 2+12.解得x=2,即OD=OF=2.
∴OB=2+2=4.
∵在Rt△ODB 中,OD= OB,∴∠B=30°.
∴∠DOB=60°. ∴S扇形ODF = ×π×22= .
则阴影部分的面积为S△ODB-S扇形ODF= ×2×2 -
=2 - .故阴影部分的面积为2 - .
小试牛刀
解:如图,过点P 作PC⊥OB,垂足为C,
则∠OCP=90°,∵∠AOB=30°,
∴PC= OP=12 cm.
(1)当r=12 cm时,r=PC,
∴⊙P 与OB 相切.
(2)当⊙P 与OB 相离时,r<PC,
∴r 需满足的条件是0 cm<r<12 cm.
如图,已知∠AOB=30°,P 是OA上的一点,OP=24cm,以r 为半径作⊙P.
(1)若r=12 cm,试判断⊙P 与射线OB 的位置关系;
(2)若⊙P 与OB 相离,试求出r 需满足的条件.
小试牛刀
7 如图,在Rt△ABC 中,∠C=90°,BE 平分∠ABC 交AC 于
点E,点D 在线段AB 上,DE⊥BE 于点E .
(1)判断直线AC 与△DBE 的外接圆的位
置关系,并证明你的结论;
(2)若AD=6,AE=6 ,求BC 的长.
解:(1)直线AC 与△DBE 的外接圆相切.
证明:∵DE⊥BE 于点E,
∴BD为 △DBE 的外接圆的直径,如图,设圆心为O,连接
OE,得OE=OB.∴∠OBE=∠OEB.
∵BE 平分∠ABC,∴∠CBE=∠OBE.
∴∠OEB=∠CBE.∴BC∥OE.
又∵∠C=90°,∴∠OEC=90°.
∴点O 到直线AC 的距离等于OE 的长.
小试牛刀
又∵OE 为△DBE 的外接圆的半径,
∴O 到直线AC 的距离等于半径.
∴直线AC 与△DBE 的外接圆相切.
(2)设OE=OD=x,在Rt△AEO 中,
AO 2=AE 2+EO 2,即(6+x)2=(6 )2+x 2,解得x=3.
∴OB=OE=OD=3,
∴AB=12,AO=9.
易证△ABC∽△AOE,
∴ ,即 ,
∴BC=4.
课堂小结
课堂小结
1.直线和圆的位置关系:相交、相切、相离.
(1)从公共点数来判断;
(2)从d 与r 间的数量关系来判断.
2.直线和圆的位置关系的性质与判定:
(1)直线和圆相离 d>r;
(2)直线和圆相切 d=r;
(3)直线和圆相交 d<r.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
