【班海精品】冀教版(新)九下-29.4 切线长定理 【优质教案】
文档属性
| 名称 | 【班海精品】冀教版(新)九下-29.4 切线长定理 【优质教案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览



文档简介
班海数学精批——一本可精细批改的教辅
切线长定理
一. 本周教学内容:
切线长定理、弦切角、和圆有关的比例线段
[学习目标]
1. 切线长概念
切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
2. 切线长定理
对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3. 弦切角、顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢?(四个)
4. 弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5. 弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6. 遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7. 与圆有关的比例线段
定理 图形 已知 结论 证法
相交弦定理 ⊙O中,AB、CD为弦,交于P PA·PB=PC·PD 连结AC、BD,证:△APC∽△DPB
相交弦定理的推论 ⊙O中,AB为直径,CD⊥AB于P PC2=PA·PB 用相交弦定理
切割线定理 ⊙O中,PT切⊙O于T,割线PB交⊙O于A PT2=PA·PB 连结TA、TB,证:△PTB∽△PAT
切割线定理推论 PB、PD为⊙O的两条割线,交⊙O于A、C PA·PB=PC·PD 过P作PT切⊙O于T,用两次切割线定理
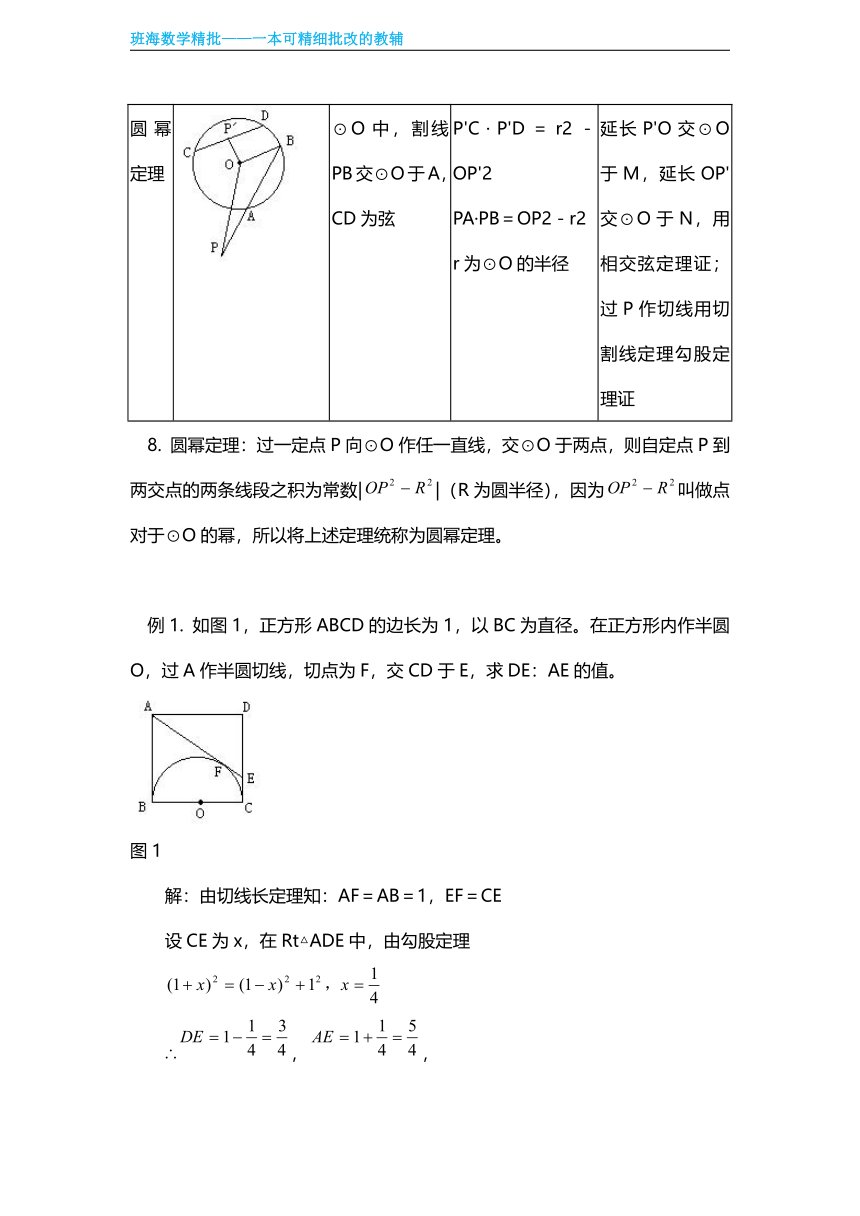
圆幂定理 ⊙O中,割线PB交⊙O于A,CD为弦 P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径 延长P'O交⊙O于M,延长OP'交⊙O于N,用相交弦定理证;过P作切线用切割线定理勾股定理证
8. 圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。
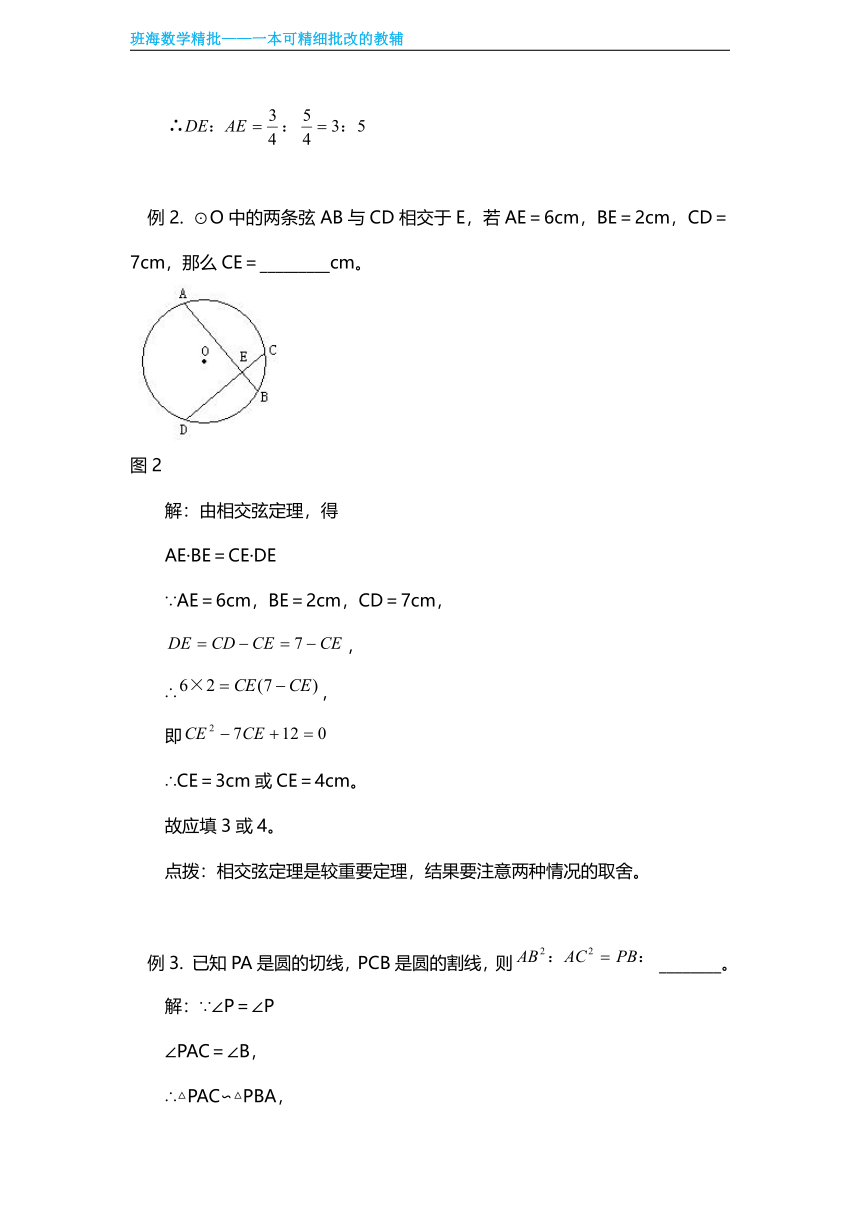
例1. 如图1,正方形ABCD的边长为1,以BC为直径。在正方形内作半圆O,过A作半圆切线,切点为F,交CD于E,求DE:AE的值。
图1
解:由切线长定理知:AF=AB=1,EF=CE
设CE为x,在Rt△ADE中,由勾股定理
∴,,
例2. ⊙O中的两条弦AB与CD相交于E,若AE=6cm,BE=2cm,CD=7cm,那么CE=_________cm。
图2
解:由相交弦定理,得
AE·BE=CE·DE
∵AE=6cm,BE=2cm,CD=7cm,
,
∴,
即
∴CE=3cm或CE=4cm。
故应填3或4。
点拨:相交弦定理是较重要定理,结果要注意两种情况的取舍。
例3. 已知PA是圆的切线,PCB是圆的割线,则________。
解:∵∠P=∠P
∠PAC=∠B,
∴△PAC∽△PBA,
∴,
∴。
又∵PA是圆的切线,PCB是圆的割线,由切割线定理,得
∴,
即 ,
故应填PC。
点拨:利用相似得出比例关系式后要注意变形,推出所需结论。
例4. 如图3,P是⊙O外一点,PC切⊙O于点C,PAB是⊙O的割线,交⊙O于A、B两点,如果PA:PB=1:4,PC=12cm,⊙O的半径为10cm,则圆心O到AB的距离是___________cm。
图3
解:∵PC是⊙O的切线,PAB是⊙O的割线,且PA:PB=1:4
∴PB=4PA
又∵PC=12cm
由切割线定理,得
∴
∴,
∴
∴PB=4×6=24(cm)
∴AB=24-6=18(cm)
设圆心O到AB距离为d cm,
由勾股定理,得
故应填。
例5. 如图4,AB为⊙O的直径,过B点作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D,(1)求证:;(2)若AB=BC=2厘米,求CE、CD的长。
图4
点悟:要证,即要证△CED∽△CBE。
证明:(1)连结BE
(2)
。
又∵,
∴厘米。
点拨:有切线,并需寻找角的关系时常添辅助线,为利用弦切角定理创造条件。
例6. 如图5,AB为⊙O的直径,弦CD∥AB,AE切⊙O于A,交CD的延长线于E。
图5
求证:
证明:连结BD,
∵AE切⊙O于A,
∴∠EAD=∠ABD
∵AE⊥AB,又AB∥CD,
∴AE⊥CD
∵AB为⊙O的直径
∴∠ADB=90°
∴∠E=∠ADB=90°
∴△ADE∽△BAD
∴
∴
∵CD∥AB
∴AD=BC,∴
例7. 如图6,PA、PC切⊙O于A、C,PDB为割线。求证:AD·BC=CD·AB
图6
点悟:由结论AD·BC=CD·AB得,显然要证△PAD∽△PBA和△PCD∽△PBC
证明:∵PA切⊙O于A,
∴∠PAD=∠PBA
又∠APD=∠BPA,
∴△PAD∽△PBA
∴
同理可证△PCD∽△PBC
∴
∵PA、PC分别切⊙O于A、C
∴PA=PC
∴
∴AD·BC=DC·AB
例8. 如图7,在直角三角形ABC中,∠A=90°,以AB边为直径作⊙O,交斜边BC于点D,过D点作⊙O的切线交AC于E。
图7
求证:BC=2OE。
点悟:由要证结论易想到应证OE是△ABC的中位线。而OA=OB,只须证AE=CE。
证明:连结OD。
∵AC⊥AB,AB为直径
∴AC为⊙O的切线,又DE切⊙O于D
∴EA=ED,OD⊥DE
∵OB=OD,∴∠B=∠ODB
在Rt△ABC中,∠C=90°-∠B
∵∠ODE=90°
∴
∴∠C=∠EDC
∴ED=EC
∴AE=EC
∴OE是△ABC的中位线
∴BC=2OE
例9. 如图8,在正方形ABCD中,AB=1,是以点B为圆心,AB长为半径的圆的一段弧。点E是边AD上的任意一点(点E与点A、D不重合),过E作所在圆的切线,交边DC于点F,G为切点。
当∠DEF=45°时,求证点G为线段EF的中点;
图8
解:由∠DEF=45°,得
,
∴∠DFE=∠DEF
∴DE=DF
又∵AD=DC
∴AE=FC
因为AB是圆B的半径,AD⊥AB,所以AD切圆B于点A;同理,CD切圆B于点C。
又因为EF切圆B于点G,所以AE=EG,FC=FG。
因此EG=FG,即点G为线段EF的中点。
【模拟试题】(答题时间:40分钟)
一、选择题
1. 已知:PA、PB切⊙O于点A、B,连结AB,若AB=8,弦AB的弦心距3,则PA=( )
A. B. C. 5 D. 8
2. 下列图形一定有内切圆的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 梯形
3. 已知:如图1直线MN与⊙O相切于C,AB为直径,∠CAB=40°,则∠MCA的度数( )
图1
A. 50° B. 40° C. 60° D. 55°
4. 圆内两弦相交,一弦长8cm且被交点平分,另一弦被交点分为1:4,则另一弦长为( )
A. 8cm B. 10cm C. 12cm D. 16cm
5. 在△ABC中,D是BC边上的点,AD,BD=3cm,DC=4cm,如果E是AD的延长线与△ABC的外接圆的交点,那么DE长等于( )
A. B.
C. D.
6. PT切⊙O于T,CT为直径,D为OC上一点,直线PD交⊙O于B和A,B在线段PD上,若CD=2,AD=3,BD=4,则PB等于( )
A. 20 B. 10 C. 5 D.
二、填空题
7. AB、CD是⊙O切线,AB∥CD,EF是⊙O的切线,它和AB、CD分别交于E、F,则∠EOF=_____________度。
8. 已知:⊙O和不在⊙O上的一点P,过P的直线交⊙O于A、B两点,若PA·PB=24,OP=5,则⊙O的半径长为_____________。
9. 若PA为⊙O的切线,A为切点,PBC割线交⊙O于B、C,若BC=20,,则PC的长为_____________。
10. 正△ABC内接于⊙O,M、N分别为AB、AC中点,延长MN交⊙O于点D,连结BD交AC于P,则_____________。
三、解答题
11. 如图2,△ABC中,AC=2cm,周长为8cm,F、K、N是△ABC与内切圆的切点,DE切⊙O于点M,且DE∥AC,求DE的长。
图2
12. 如图3,已知P为⊙O的直径AB延长线上一点,PC切⊙O于C,CD⊥AB于D,求证:CB平分∠DCP。
图3
13. 如图4,已知AD为⊙O的直径,AB是⊙O的切线,过B的割线BMN交AD的延长线于C,且BM=MN=NC,若AB,求⊙O的半径。
图4
[参考答案]
一、选择题
1. A 2. C 3. A 4. B 5. B 6. A
二、填空题
7. 90 8. 1 9. 30 10.
三、解答题:
11. 由切线长定理得△BDE周长为4,由△BDE∽△BAC,得DE=1cm
12. 证明:连结AC,则AC⊥CB
∵CD⊥AB,∴△ACB∽△CDB,∴∠A=∠1
∵PC为⊙O的切线,∴∠A=∠2,又∠1=∠2,
∴BC平分∠DCP
13. 设BM=MN=NC=xcm
又∵
∴
又∵OA是过切点A的半径,∴OA⊥AB即AC⊥AB
在Rt△ABC中,由勾股定理,得,
由割线定理:,又∵
∴
∴半径为。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
切线长定理
一. 本周教学内容:
切线长定理、弦切角、和圆有关的比例线段
[学习目标]
1. 切线长概念
切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
2. 切线长定理
对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3. 弦切角、顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢?(四个)
4. 弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5. 弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6. 遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7. 与圆有关的比例线段
定理 图形 已知 结论 证法
相交弦定理 ⊙O中,AB、CD为弦,交于P PA·PB=PC·PD 连结AC、BD,证:△APC∽△DPB
相交弦定理的推论 ⊙O中,AB为直径,CD⊥AB于P PC2=PA·PB 用相交弦定理
切割线定理 ⊙O中,PT切⊙O于T,割线PB交⊙O于A PT2=PA·PB 连结TA、TB,证:△PTB∽△PAT
切割线定理推论 PB、PD为⊙O的两条割线,交⊙O于A、C PA·PB=PC·PD 过P作PT切⊙O于T,用两次切割线定理
圆幂定理 ⊙O中,割线PB交⊙O于A,CD为弦 P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径 延长P'O交⊙O于M,延长OP'交⊙O于N,用相交弦定理证;过P作切线用切割线定理勾股定理证
8. 圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。
例1. 如图1,正方形ABCD的边长为1,以BC为直径。在正方形内作半圆O,过A作半圆切线,切点为F,交CD于E,求DE:AE的值。
图1
解:由切线长定理知:AF=AB=1,EF=CE
设CE为x,在Rt△ADE中,由勾股定理
∴,,
例2. ⊙O中的两条弦AB与CD相交于E,若AE=6cm,BE=2cm,CD=7cm,那么CE=_________cm。
图2
解:由相交弦定理,得
AE·BE=CE·DE
∵AE=6cm,BE=2cm,CD=7cm,
,
∴,
即
∴CE=3cm或CE=4cm。
故应填3或4。
点拨:相交弦定理是较重要定理,结果要注意两种情况的取舍。
例3. 已知PA是圆的切线,PCB是圆的割线,则________。
解:∵∠P=∠P
∠PAC=∠B,
∴△PAC∽△PBA,
∴,
∴。
又∵PA是圆的切线,PCB是圆的割线,由切割线定理,得
∴,
即 ,
故应填PC。
点拨:利用相似得出比例关系式后要注意变形,推出所需结论。
例4. 如图3,P是⊙O外一点,PC切⊙O于点C,PAB是⊙O的割线,交⊙O于A、B两点,如果PA:PB=1:4,PC=12cm,⊙O的半径为10cm,则圆心O到AB的距离是___________cm。
图3
解:∵PC是⊙O的切线,PAB是⊙O的割线,且PA:PB=1:4
∴PB=4PA
又∵PC=12cm
由切割线定理,得
∴
∴,
∴
∴PB=4×6=24(cm)
∴AB=24-6=18(cm)
设圆心O到AB距离为d cm,
由勾股定理,得
故应填。
例5. 如图4,AB为⊙O的直径,过B点作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D,(1)求证:;(2)若AB=BC=2厘米,求CE、CD的长。
图4
点悟:要证,即要证△CED∽△CBE。
证明:(1)连结BE
(2)
。
又∵,
∴厘米。
点拨:有切线,并需寻找角的关系时常添辅助线,为利用弦切角定理创造条件。
例6. 如图5,AB为⊙O的直径,弦CD∥AB,AE切⊙O于A,交CD的延长线于E。
图5
求证:
证明:连结BD,
∵AE切⊙O于A,
∴∠EAD=∠ABD
∵AE⊥AB,又AB∥CD,
∴AE⊥CD
∵AB为⊙O的直径
∴∠ADB=90°
∴∠E=∠ADB=90°
∴△ADE∽△BAD
∴
∴
∵CD∥AB
∴AD=BC,∴
例7. 如图6,PA、PC切⊙O于A、C,PDB为割线。求证:AD·BC=CD·AB
图6
点悟:由结论AD·BC=CD·AB得,显然要证△PAD∽△PBA和△PCD∽△PBC
证明:∵PA切⊙O于A,
∴∠PAD=∠PBA
又∠APD=∠BPA,
∴△PAD∽△PBA
∴
同理可证△PCD∽△PBC
∴
∵PA、PC分别切⊙O于A、C
∴PA=PC
∴
∴AD·BC=DC·AB
例8. 如图7,在直角三角形ABC中,∠A=90°,以AB边为直径作⊙O,交斜边BC于点D,过D点作⊙O的切线交AC于E。
图7
求证:BC=2OE。
点悟:由要证结论易想到应证OE是△ABC的中位线。而OA=OB,只须证AE=CE。
证明:连结OD。
∵AC⊥AB,AB为直径
∴AC为⊙O的切线,又DE切⊙O于D
∴EA=ED,OD⊥DE
∵OB=OD,∴∠B=∠ODB
在Rt△ABC中,∠C=90°-∠B
∵∠ODE=90°
∴
∴∠C=∠EDC
∴ED=EC
∴AE=EC
∴OE是△ABC的中位线
∴BC=2OE
例9. 如图8,在正方形ABCD中,AB=1,是以点B为圆心,AB长为半径的圆的一段弧。点E是边AD上的任意一点(点E与点A、D不重合),过E作所在圆的切线,交边DC于点F,G为切点。
当∠DEF=45°时,求证点G为线段EF的中点;
图8
解:由∠DEF=45°,得
,
∴∠DFE=∠DEF
∴DE=DF
又∵AD=DC
∴AE=FC
因为AB是圆B的半径,AD⊥AB,所以AD切圆B于点A;同理,CD切圆B于点C。
又因为EF切圆B于点G,所以AE=EG,FC=FG。
因此EG=FG,即点G为线段EF的中点。
【模拟试题】(答题时间:40分钟)
一、选择题
1. 已知:PA、PB切⊙O于点A、B,连结AB,若AB=8,弦AB的弦心距3,则PA=( )
A. B. C. 5 D. 8
2. 下列图形一定有内切圆的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 梯形
3. 已知:如图1直线MN与⊙O相切于C,AB为直径,∠CAB=40°,则∠MCA的度数( )
图1
A. 50° B. 40° C. 60° D. 55°
4. 圆内两弦相交,一弦长8cm且被交点平分,另一弦被交点分为1:4,则另一弦长为( )
A. 8cm B. 10cm C. 12cm D. 16cm
5. 在△ABC中,D是BC边上的点,AD,BD=3cm,DC=4cm,如果E是AD的延长线与△ABC的外接圆的交点,那么DE长等于( )
A. B.
C. D.
6. PT切⊙O于T,CT为直径,D为OC上一点,直线PD交⊙O于B和A,B在线段PD上,若CD=2,AD=3,BD=4,则PB等于( )
A. 20 B. 10 C. 5 D.
二、填空题
7. AB、CD是⊙O切线,AB∥CD,EF是⊙O的切线,它和AB、CD分别交于E、F,则∠EOF=_____________度。
8. 已知:⊙O和不在⊙O上的一点P,过P的直线交⊙O于A、B两点,若PA·PB=24,OP=5,则⊙O的半径长为_____________。
9. 若PA为⊙O的切线,A为切点,PBC割线交⊙O于B、C,若BC=20,,则PC的长为_____________。
10. 正△ABC内接于⊙O,M、N分别为AB、AC中点,延长MN交⊙O于点D,连结BD交AC于P,则_____________。
三、解答题
11. 如图2,△ABC中,AC=2cm,周长为8cm,F、K、N是△ABC与内切圆的切点,DE切⊙O于点M,且DE∥AC,求DE的长。
图2
12. 如图3,已知P为⊙O的直径AB延长线上一点,PC切⊙O于C,CD⊥AB于D,求证:CB平分∠DCP。
图3
13. 如图4,已知AD为⊙O的直径,AB是⊙O的切线,过B的割线BMN交AD的延长线于C,且BM=MN=NC,若AB,求⊙O的半径。
图4
[参考答案]
一、选择题
1. A 2. C 3. A 4. B 5. B 6. A
二、填空题
7. 90 8. 1 9. 30 10.
三、解答题:
11. 由切线长定理得△BDE周长为4,由△BDE∽△BAC,得DE=1cm
12. 证明:连结AC,则AC⊥CB
∵CD⊥AB,∴△ACB∽△CDB,∴∠A=∠1
∵PC为⊙O的切线,∴∠A=∠2,又∠1=∠2,
∴BC平分∠DCP
13. 设BM=MN=NC=xcm
又∵
∴
又∵OA是过切点A的半径,∴OA⊥AB即AC⊥AB
在Rt△ABC中,由勾股定理,得,
由割线定理:,又∵
∴
∴半径为。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
