【班海精品】人教版(新)九下-27.2 相似三角形 第四课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-27.2 相似三角形 第四课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览









文档简介
(共39张PPT)
27.2 相似三角形
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
2.(简称:三边):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
相似三角形的判定:
1.(简称:平行线)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
新课精讲
探索新知
1
知识点
两边成比例且夹角相等的两个三角形相似
问 题
利用刻度尺和量角器画△ABC 与△A1B1C1,使∠A=∠A1, 和 都等于给定的值k,量出它们的第三组对应边BC 和B1C1的长,它们的比等于k 吗?另外两组对应角∠B 与∠B1,∠C 与∠C1是否相等?
探索新知
A
B
C
A1
B1
C1
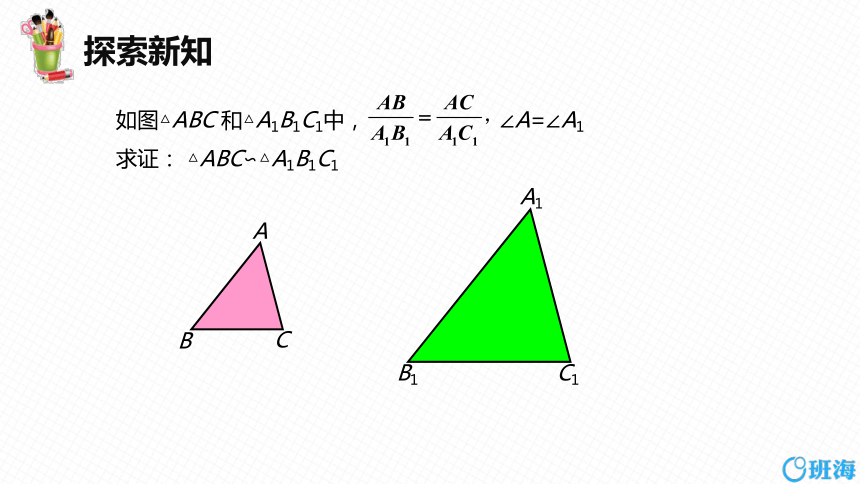
如图△ABC 和△A1B1C1中, ∠A=∠A1
求证: △ABC∽△A1B1C1
探索新知
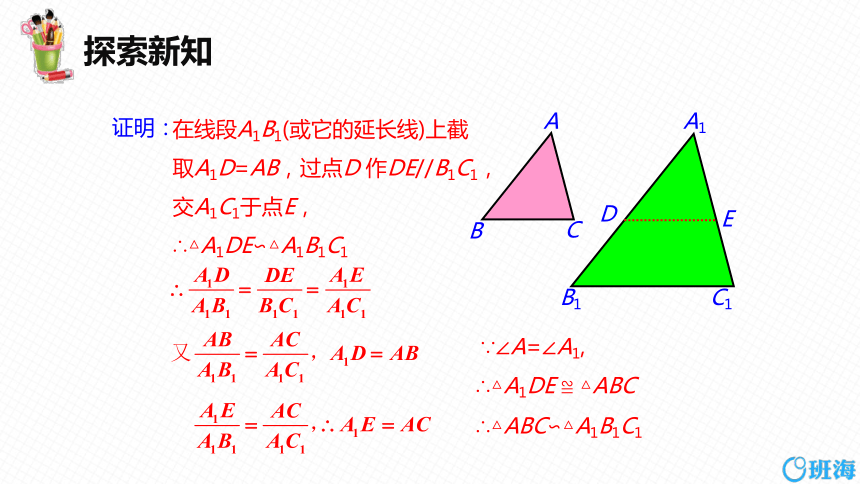
在线段A1B1(或它的延长线)上截
取A1D=AB,过点D 作DE//B1C1,
交A1C1于点E,
∴△A1DE∽△A1B1C1
证明:
A1
B1
C1
A
B
C
D
E
∵∠A=∠A1,
∴△A1DE ≌ △ABC
∴△ABC∽△A1B1C1
探索新知
结 论:
判定定理2:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
可以简单说成:两边对应成比例且夹角相等,两三角形相似.
探索新知
例1 根据下列条件,判断 是否相似,并说
明理由.∠A=120°,AB=7cm, AC=14cm. ∠A ′=120°,
A′B ′=3cm, A′C ′=6cm.
解:
探索新知
总 结
利用三角形两边成比例且夹角相等证两三角形相似的方法:
首先找出两个三角形中相等的那个角;再分别找出两个三角形中夹这个角的两条边,并按大小排列找出对应边;最后看这两组对应边是否成比例,若成比例则两个三角形相似,否则不相似.
典题精讲
1
根据下列条件,判断 是否相似,并说明理由.
∠A=40°, AB=8cm, AC=15cm.
∠A′=40°,A′B ′=16cm, A′C ′=30cm.
解:相似
又∵∠A=∠A′=40°,
∴△ABC∽△A′B′C ′.
典题精讲
图中的两个三角形是否相似?为什么?
2
相似
理由如下:
∵
∴
又∵∠ACB=∠ECD,
∴这两个三角形相似.
解:
B
E
典题精讲
3
在等边三角形ABC 中,D,E 分别在AC,AB上,且 ,AE=BE,则有( )
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
B
典题精讲
4
不能判定△ABC 和△A′B′C′ 相似的条件是( )
A.
B. ,且∠A=∠A′
C. ,且∠B=∠A′
D. ,且∠B=∠C′
D
错解:设AE 的长为x. ∠A是公共角,
要使△ADE 和△ABC 相似,
则有
解得x=6.所以AE 的长为6.
探索新知
2
知识点
判定三角形相似的应用
例2 如图,在△ABC 中,AB=16,AC=8,在AC 上取一
点D,使AD=3,如果在AB上取点E,使△ADE 和△ABC
相似,求AE 的长.
探索新知
错解分析:已知有一对角相等,要使这两个三角形相似,夹
这对角的两边对应成比例.但两边的对应关系无
法确定,所以应分两种情况考虑.
正解:设AE 的长为x. ∠A是公共角,
要使△ADE 和△ABC 相似,
则有
即
解得x=6或x=1.5.
所以AE 的长为6或1.5.
探索新知
总 结
判定两个三角形相似,当已知有两边成比例,可证明第三边也与这两边成比例,也可证明夹角相等;若已知有一对角相等,则可证明夹这对角的两边对应成比例.当无法确定对应关系时,必须进行分类讨论.
典题精讲
如图,在△ABC 中,AB=8,AC=6,点D 在AC上,且AD=2,如果要在AB上找一点E,使△ADE 与△ABC 相似,那么AE=
______________.
1
典题精讲
如图,在方格纸中,△ABC 和△EPD 的顶点均在格点上,要使△ABC∽△EPD,则点P 所在的格点为( )
A.P1
B.P2
C.P3
D.P4
2
C
易错提醒
已知△ABC 和△A′B′C ′,∠A=50°,∠A′=50°,AB=8,BC=7,A′B ′=16,B′C ′=14,请问这两个三角形是否相似?请说明你的理由.
易错点: 在应用边角关系判定三角形相似时,忽略“夹角”而致错.
解:
△ABC 与△A′B′C ′不一定相似.理由如下:因为∠A=∠A′=50°,但不知道 是否等于 ,所以根据已知条件不能确定△ABC 与△A′B′C ′相似.
易错提醒
易错总结:根据边角关系判定两个三角形相似,应具备
“两边对应成比例,且夹角相等”,本题中虽然
,但BC,B′C ′分别是∠A,∠A′的对边,不
满足“两边成比例且夹角相等”,不能由此来判断△ABC与△A′B′C ′相似.
学以致用
小试牛刀
1
如图,四边形ABCD 的对角线AC,BD 相交于点O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
B
小试牛刀
2
如图,D 是△ABC 的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件可以是( )
A.
B.
C.CD 2=AD·DB
D.AC 2=AD·AB
D
小试牛刀
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连接,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
A. B.
C. D.
3
D
小试牛刀
4 如图,在△ABC 中,点D,E 分别在边AB,AC上,∠AED=∠B,射线AG 分别交线段DE,BC 于点F,G,且
(1)求证:△ADF∽△ACG;
(2)若 ,求 的值.
小试牛刀
(1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C.
又∵
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,∴
又∵ ,∴
∴
小试牛刀
5 如图,在△ABC中,AB=AC=1,BC= ,在AC 边上截取AD=BC,连接BD.
(1)通过计算,判断AD 2与AC·CD 的大小关系;
(2)求∠ABD 的度数.
小试牛刀
解:
(1)通过计算,判断AD 2与AC·CD 的大小关系;
∵AB=AC=1,BC= ,AD=BC,
∴AD= ,DC=AC-AD=1- =
∴AD 2= ,
AC·CD=1×
∴AD 2=AC·CD.
小试牛刀
(2)求∠ABD 的度数.
解:
∵AD=BC,AD 2=AC·CD,
∴BC 2=AC·CD,即
又∵∠C=∠C,∴△BCD∽△ACB.
∴ ,∠DBC=∠A.
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°.
解得x=36°. ∴∠ABD=36°.
小试牛刀
6 如图,在正方形ABCD 中,E,F 分别是边AD,CD上的点,AE=ED,DF= DC,连接EF 并延长,交BC 的延长线于点G,连接BE.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG 的长.
小试牛刀
证明:
(1)求证:△ABE∽△DEF;
在正方形ABCD 中,∠A=∠D=90°,AB=AD=CD.
∵AE=ED,DF= DC,
∴AE=ED= AB,DF= AB,
∴ . ∴△ABE∽△DEF.
小试牛刀
解:
(2)若正方形的边长为4,求BG 的长.
∵DF= DC,∴
∵AD∥CG,∴△EFD∽△GFC,
∴
∵DE= AB=2,∴CG=6,∴BG=10.
小试牛刀
7 如图,在矩形ABCD 中,AB=10 cm,BC=20 cm,两只小虫P和Q 同时分别从A,B 出发沿AB,BC 向终点B,C 方向前进,小虫P 每秒走1 cm,小虫Q 每秒走2 cm.
请问:它们同时出发多少秒时,以P,B,Q 为顶点的三角形与以A,B,C 为顶点的三角形相似?
小试牛刀
解:
设它们同时出发了t s时△PBQ 与△ABC 相似,此时,
BP=(10-t ) cm,BQ=2t cm.
①∵∠B=∠B,∴当 时,△PBQ∽△ABC.
∴ ∴t=5;
②∵∠B=∠B,∴当 时,△PBQ∽△CBA.
∴
∴t=2.
综上,它们同时出发了2 s或5 s时,以P,B,Q 为顶点
的三角形与以A,B,C 为顶点的三角形相似.
课堂小结
课堂小结
(1)要识别两个三角形相似,要找到这两个三角形有
两边成比例,再找到上述两边的夹角相等,即可
判定这两个三角形相似.
(2)当题目中告诉两个三角形某些边的长度,又有对
顶角或公共角或告诉了某个角的度数时,我们要
首先考虑这个判定方法.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.2 相似三角形
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
2.(简称:三边):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
相似三角形的判定:
1.(简称:平行线)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
新课精讲
探索新知
1
知识点
两边成比例且夹角相等的两个三角形相似
问 题
利用刻度尺和量角器画△ABC 与△A1B1C1,使∠A=∠A1, 和 都等于给定的值k,量出它们的第三组对应边BC 和B1C1的长,它们的比等于k 吗?另外两组对应角∠B 与∠B1,∠C 与∠C1是否相等?
探索新知
A
B
C
A1
B1
C1
如图△ABC 和△A1B1C1中, ∠A=∠A1
求证: △ABC∽△A1B1C1
探索新知
在线段A1B1(或它的延长线)上截
取A1D=AB,过点D 作DE//B1C1,
交A1C1于点E,
∴△A1DE∽△A1B1C1
证明:
A1
B1
C1
A
B
C
D
E
∵∠A=∠A1,
∴△A1DE ≌ △ABC
∴△ABC∽△A1B1C1
探索新知
结 论:
判定定理2:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
可以简单说成:两边对应成比例且夹角相等,两三角形相似.
探索新知
例1 根据下列条件,判断 是否相似,并说
明理由.∠A=120°,AB=7cm, AC=14cm. ∠A ′=120°,
A′B ′=3cm, A′C ′=6cm.
解:
探索新知
总 结
利用三角形两边成比例且夹角相等证两三角形相似的方法:
首先找出两个三角形中相等的那个角;再分别找出两个三角形中夹这个角的两条边,并按大小排列找出对应边;最后看这两组对应边是否成比例,若成比例则两个三角形相似,否则不相似.
典题精讲
1
根据下列条件,判断 是否相似,并说明理由.
∠A=40°, AB=8cm, AC=15cm.
∠A′=40°,A′B ′=16cm, A′C ′=30cm.
解:相似
又∵∠A=∠A′=40°,
∴△ABC∽△A′B′C ′.
典题精讲
图中的两个三角形是否相似?为什么?
2
相似
理由如下:
∵
∴
又∵∠ACB=∠ECD,
∴这两个三角形相似.
解:
B
E
典题精讲
3
在等边三角形ABC 中,D,E 分别在AC,AB上,且 ,AE=BE,则有( )
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
B
典题精讲
4
不能判定△ABC 和△A′B′C′ 相似的条件是( )
A.
B. ,且∠A=∠A′
C. ,且∠B=∠A′
D. ,且∠B=∠C′
D
错解:设AE 的长为x. ∠A是公共角,
要使△ADE 和△ABC 相似,
则有
解得x=6.所以AE 的长为6.
探索新知
2
知识点
判定三角形相似的应用
例2 如图,在△ABC 中,AB=16,AC=8,在AC 上取一
点D,使AD=3,如果在AB上取点E,使△ADE 和△ABC
相似,求AE 的长.
探索新知
错解分析:已知有一对角相等,要使这两个三角形相似,夹
这对角的两边对应成比例.但两边的对应关系无
法确定,所以应分两种情况考虑.
正解:设AE 的长为x. ∠A是公共角,
要使△ADE 和△ABC 相似,
则有
即
解得x=6或x=1.5.
所以AE 的长为6或1.5.
探索新知
总 结
判定两个三角形相似,当已知有两边成比例,可证明第三边也与这两边成比例,也可证明夹角相等;若已知有一对角相等,则可证明夹这对角的两边对应成比例.当无法确定对应关系时,必须进行分类讨论.
典题精讲
如图,在△ABC 中,AB=8,AC=6,点D 在AC上,且AD=2,如果要在AB上找一点E,使△ADE 与△ABC 相似,那么AE=
______________.
1
典题精讲
如图,在方格纸中,△ABC 和△EPD 的顶点均在格点上,要使△ABC∽△EPD,则点P 所在的格点为( )
A.P1
B.P2
C.P3
D.P4
2
C
易错提醒
已知△ABC 和△A′B′C ′,∠A=50°,∠A′=50°,AB=8,BC=7,A′B ′=16,B′C ′=14,请问这两个三角形是否相似?请说明你的理由.
易错点: 在应用边角关系判定三角形相似时,忽略“夹角”而致错.
解:
△ABC 与△A′B′C ′不一定相似.理由如下:因为∠A=∠A′=50°,但不知道 是否等于 ,所以根据已知条件不能确定△ABC 与△A′B′C ′相似.
易错提醒
易错总结:根据边角关系判定两个三角形相似,应具备
“两边对应成比例,且夹角相等”,本题中虽然
,但BC,B′C ′分别是∠A,∠A′的对边,不
满足“两边成比例且夹角相等”,不能由此来判断△ABC与△A′B′C ′相似.
学以致用
小试牛刀
1
如图,四边形ABCD 的对角线AC,BD 相交于点O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
B
小试牛刀
2
如图,D 是△ABC 的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件可以是( )
A.
B.
C.CD 2=AD·DB
D.AC 2=AD·AB
D
小试牛刀
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连接,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
A. B.
C. D.
3
D
小试牛刀
4 如图,在△ABC 中,点D,E 分别在边AB,AC上,∠AED=∠B,射线AG 分别交线段DE,BC 于点F,G,且
(1)求证:△ADF∽△ACG;
(2)若 ,求 的值.
小试牛刀
(1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C.
又∵
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,∴
又∵ ,∴
∴
小试牛刀
5 如图,在△ABC中,AB=AC=1,BC= ,在AC 边上截取AD=BC,连接BD.
(1)通过计算,判断AD 2与AC·CD 的大小关系;
(2)求∠ABD 的度数.
小试牛刀
解:
(1)通过计算,判断AD 2与AC·CD 的大小关系;
∵AB=AC=1,BC= ,AD=BC,
∴AD= ,DC=AC-AD=1- =
∴AD 2= ,
AC·CD=1×
∴AD 2=AC·CD.
小试牛刀
(2)求∠ABD 的度数.
解:
∵AD=BC,AD 2=AC·CD,
∴BC 2=AC·CD,即
又∵∠C=∠C,∴△BCD∽△ACB.
∴ ,∠DBC=∠A.
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°.
解得x=36°. ∴∠ABD=36°.
小试牛刀
6 如图,在正方形ABCD 中,E,F 分别是边AD,CD上的点,AE=ED,DF= DC,连接EF 并延长,交BC 的延长线于点G,连接BE.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG 的长.
小试牛刀
证明:
(1)求证:△ABE∽△DEF;
在正方形ABCD 中,∠A=∠D=90°,AB=AD=CD.
∵AE=ED,DF= DC,
∴AE=ED= AB,DF= AB,
∴ . ∴△ABE∽△DEF.
小试牛刀
解:
(2)若正方形的边长为4,求BG 的长.
∵DF= DC,∴
∵AD∥CG,∴△EFD∽△GFC,
∴
∵DE= AB=2,∴CG=6,∴BG=10.
小试牛刀
7 如图,在矩形ABCD 中,AB=10 cm,BC=20 cm,两只小虫P和Q 同时分别从A,B 出发沿AB,BC 向终点B,C 方向前进,小虫P 每秒走1 cm,小虫Q 每秒走2 cm.
请问:它们同时出发多少秒时,以P,B,Q 为顶点的三角形与以A,B,C 为顶点的三角形相似?
小试牛刀
解:
设它们同时出发了t s时△PBQ 与△ABC 相似,此时,
BP=(10-t ) cm,BQ=2t cm.
①∵∠B=∠B,∴当 时,△PBQ∽△ABC.
∴ ∴t=5;
②∵∠B=∠B,∴当 时,△PBQ∽△CBA.
∴
∴t=2.
综上,它们同时出发了2 s或5 s时,以P,B,Q 为顶点
的三角形与以A,B,C 为顶点的三角形相似.
课堂小结
课堂小结
(1)要识别两个三角形相似,要找到这两个三角形有
两边成比例,再找到上述两边的夹角相等,即可
判定这两个三角形相似.
(2)当题目中告诉两个三角形某些边的长度,又有对
顶角或公共角或告诉了某个角的度数时,我们要
首先考虑这个判定方法.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
