【班海精品】人教版(新)九下-27.2 相似三角形 第五课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-27.2 相似三角形 第五课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览










文档简介
(共47张PPT)
27.2 相似三角形
第5课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾:
三角形的内角和是多少度?
新课精讲
探索新知
1
知识点
两角分别相等的两个三角形相似
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺 , 相似吗?
探索新知
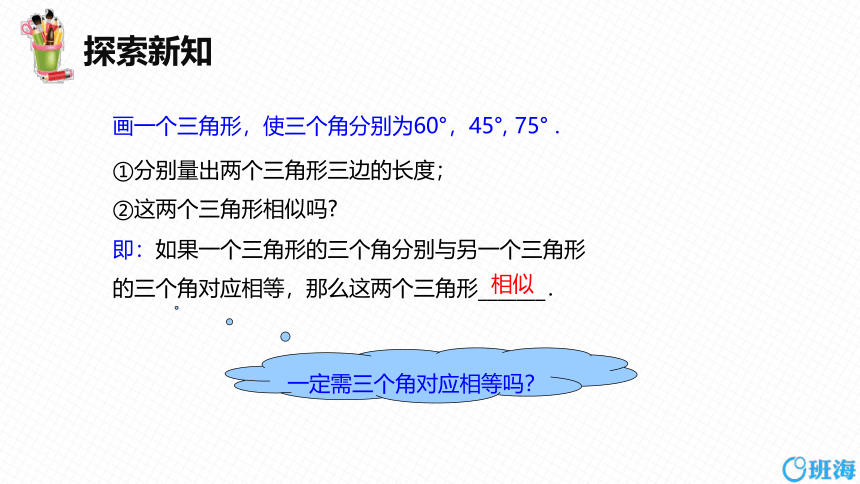
画一个三角形,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;
②这两个三角形相似吗
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角对应相等吗?
探索新知
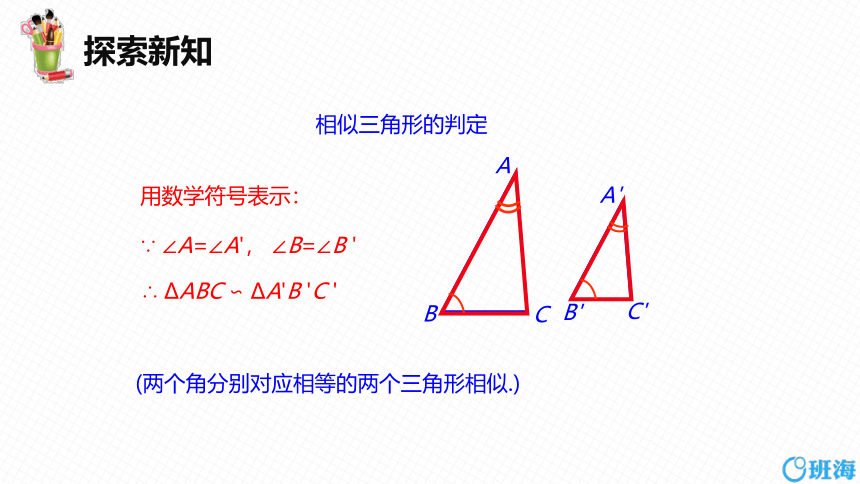
相似三角形的判别方法1:
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似吗?
探索新知
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B '
∴ ΔABC ∽ ΔA'B 'C '
用数学符号表示:
相似三角形的判定
(两个角分别对应相等的两个三角形相似.)
探索新知
例1 如图,Rt△ABC 中,∠C=90°,AB=10,AC=8.E 是AC上
一 点,AE=5,ED⊥AB,垂足为D,求AD 的长.
解:∵ ED⊥AB,
∴ ∠EDA=90°.
又∠C=90 °, ∠A=∠A,
∴△AED∽△ABC.
A
D
B
C
E
探索新知
总 结
当两个三角形已具备一角对应相等的条件时,往往先找是否有另一角对应相等,当此思路不通时,再找夹等角的两边对应成比例.找角相等时应注意挖掘公共角、对顶角、同角的余角(或补角)等.
典题精讲
底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.
1
底角相等的两个等腰三角形相似.已知:在△ABC 中,AB=AC,在△A′B′C ′中,A′B ′=A′C ′,且∠B=∠B ′. 求证:△ABC∽△A′B′C ′.证明:在△ABC 中,∵AB=AC,∴∠B=∠C,同理∠B ′=∠C ′.又∵∠B=∠B ′,∴∠C=∠C ′. ∴△ABC∽△A′B′C ′. 顶角相等的两个等腰三角形相似.已知:在△ABC 中,AB=AC,在△A′B′C ′中,A′B ′=A′C ′,且∠A=∠A′.求证:△ABC∽△A′B′C ′.证明:在△ABC 中,∵AB=AC,∴∠B=∠C,同理∠B ′=∠C ′.又∵∠B= ∠B′=
∠A=∠A′,∴∠B=∠B ′.又∵∠A=∠A′,∴△ABC∽△A′B′C ′.
解:
典题精讲
2
下列各组条件中,不能判定△ABC 与△A′B′C′ 相似的是( )
A.∠A=∠A′,∠B=∠B′
B.∠C=∠C′=90°,∠A=35°,∠B′=55°
C.∠A=∠B,∠A′=∠B′
D.∠A+∠B=∠A′+∠B ′,∠A-∠B=∠A′-∠B ′
C
典题精讲
3
如图,△ABC 中,∠A=78°,AB=4,AC=6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
C
典题精讲
4
如图,△ABC 和△ADE 均为等边三角形,D 在BC 上,DE 与AC 相交于点F,AB=9,BD=3,则CF 等于( )
A.1
B.2
C.3
D.4
B
探索新知
2
知识点
两直角三角形相似的判定
思考:
我们知道,两个直角三角形全等可以用“HL”来判定.
那么,满足斜边和一条直角边成比例的两个直角三角形相似吗?
事实上,这两个直角三角形相似.下面我们给出证明.
如图,在Rt△ABC 和Rt△A′B′C′ 中, ∠C=90°,∠C′=90°,
求证: Rt△ABC∽Rt△A′B′C′ .
探索新知
分析:要证Rt△ABC∽Rt△A′B′C′ ,可设法证
∴Rt△ABC∽Rt△A′B′C′.
探索新知
归 纳
直角三角形相似的判定定理:
(1)有一锐角相等的两个直角三角形相似;
(2)有两组直角边对应成比例的两直角三角形相似.
数学表达式:
在Rt△ABC 和Rt△A′B′C′ 中,
(1)∵∠C=∠C′=90°,∠A=∠A′,∴Rt△ABC∽Rt△A′B′C ′;
(2)∵∠C=∠C′=90°,
∴Rt△ABC∽Rt△A′B′C ′.
探索新知
归 纳
直角三角形相似的判定方法:
有一锐角对应相等 两直角三角形相似
有两组直角边对应成比例 两直角三角形相似
有斜边与一直角边对应成比例 两直角三角形相似
探索新知
例2 在Rt△ABC 和Rt△DEF 中,∠C=∠F=90°,下列条
件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
导引:根据相似三角形的判定方法对各个选项进行分析即可.
A.∵∠A=55°,∴∠B=90°-55°=35°.
∵∠D=35°,∴∠B=∠D.
又∵∠C=∠F=90°,∴△ABC∽△EDF;
C
探索新知
B.∵AC=9,BC=12,DF=6,EF=8,
∴
又∵∠C=∠F=90°,∴△ABC∽△DEF;
C.由题目中知∠C=∠F=90°,但已知条件中不能得出两
组对应边成比例,故不能判定两三角形相似.
D.∵AB=10,AC=8,∴由勾股定理可得BC=6.
又DE=15,EF=9,∴
又∵∠C=∠F=90°,∴△ABC∽△DEF.
探索新知
总 结
判定两直角三角形相似的方法:
一个锐角对应相等,两组直角边对应成比例,斜边和一直角边对应成比例.
典题精讲
如图,Rt△ABC 中,CD 是斜边AB上的高.
求证:(1)△ACD∽△ABC; (2)△CBD∽△ABC.
1
(1)∵CD 是斜边AB上的高,∴∠ADC=90°.
在Rt△ABC 中,∠ACB=90°,
∴∠ADC=∠ACB.
又∵∠A=∠A,∴△ACD∽△ABC.
(2)∵CD 是斜边AB上的高,
∴∠CDB=90°.
在Rt△ABC 中,∠ACB=90°,
∴∠CDB=∠ACB.
又∵∠B=∠B,∴△CBD∽△ABC.
证明:
D
B
C
A
典题精讲
如果Rt△ABC 的两条直角边分别为3和4,那么以3k 和4k (k是正整数)为直角边的直角三角形一定与Rt△ABC 相似吗?为什么?
2
一定相似.理由如下:
∵两条对应直角边的比分别为
∴对应直角边的比相等.
又∵两直角边所夹的角都为直角,
∴两个三角形一定相似.
证明:
典题精讲
如图,矩形ABCD 中,AB=8,BC=4,点E 在AB上,点F 在CD上,点G,H 在对角线AC上,若四边形EGFH 是菱形,则AE 的长是( )
A.2 B.3 C.5 D.6
3
C
典题精讲
如图,正方形ABCD 中,M 为BC上一点,ME⊥AM,ME 交AD 的延长线于点E. 若AB=12,BM=5,则DE 的长为( )
A.18 B. C. D.
4
B
易错提醒
已知正方形ABCD 的边长为1,P 是CD 边的中点,Q 在线段BC上,△ADP 与△QCP 相似时,求BQ 的值.
解:
由题意,得∠D=∠C=90°.
①当 时,△ADP∽△PCQ,
即 ,得CQ= .故BQ=1- =
易错提醒
易错点: 相似情形考虑不全面,解答不完整.
跳出误区:因为题中∠D=∠C=90°,所以直角三角形相似在对应顺序上有两种可能,即△ADP∽△PCQ 或△ADP∽△QCP,此题容易因只考虑一种情况而漏解.
②当 时,△ADP∽△QCP,
即 ,得QC=1,故BQ=0.
所以当△ADP 与△QCP 相似时,BQ 的值为0或
学以致用
小试牛刀
1
如图,AB 是半圆O 的直径,D,E 是半圆上任意两点,连接AD,DE,AE 与BD 相交于点C,要使△ADC 与△ABD 相似,下列添加的条件错误的是( )
A.∠ACD=∠DAB
B.AD=DE
C.AD 2=BD·CD
D.CD·AB=AC·BD
D
小试牛刀
2
如图,在△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段AC 的长为( )
A.4
B.4
C.6
D.4
B
小试牛刀
3
如图,矩形ABCD 的边AD=3,AB=2,E 为AB 的中点,F 在边BC上,且BF=2FC,AF 分别与DE,DB 相交于点M,N,则MN 的长为( )
A.
B.
C.
D.
B
小试牛刀
如图,在△ABC 中,∠ACB=90°,CD⊥AB 于点D,下列结论中:
①AC·BC=AB·CD;②AC 2=AD·DB;③BC 2=BD·BA;④CD 2=AD·DB,正确的个数是( )
A.1
B.2
C.3
D.4
4
C
小试牛刀
5 如图,正方形ABCD 的顶点A 在等腰直角三角形DEF 的斜边EF上,EF 与BC 相交于点G,连接CF.
(1)求证:△DAE ≌ △DCF;
(2)求证:△ABG ∽ △CFG.
小试牛刀
在正方形ABCD、等腰直角三角形DEF 中,
∠ADC=∠EDF=90°,DA=DC,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF.
∴∠ADE=∠CDF.
在△ADE 和△CDF 中,
∴△ADE ≌ △CDF.
证明:
(1)求证:△DAE ≌ △DCF;
小试牛刀
如图,延长BA到M,交ED于点M.
∵△ADE ≌ △CDF,
∴∠EAD=∠FCD,即
∠EAM+∠MAD=∠BCF+∠BCD.
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF.
∵∠EAM=∠BAG,∴∠BAG=∠BCF.
∵∠AGB=∠CGF,∴△ABG∽△CFG.
证明:
(2)求证:△ABG∽△CFG.
小试牛刀
6 如图,AB 为半圆O 的直径,C 为BA 延长线上一点,CD 切半圆O于点D,连接OD. 作BE⊥CD 于点E,交半圆O 于点F. 已知CE=12,BE=9.
(1)求证:△COD ∽△CBE;
(2)求半圆O 的半径r 的长.
小试牛刀
∵CD 切半圆O 于点D,∴CD⊥OD,∴∠CDO=90°.
∵BE⊥CD,∴∠CDO=90°=∠E.
又∵∠C=∠C,∴△COD∽△CBE.
证明:
(1)求证:△COD∽△CBE;
解:
(2)求半圆O 的半径r 的长.
在Rt△BEC 中,CE=12,BE=9,
∴BC=
∵△COD∽△CBE,
∴ ,即 ,解得r=
小试牛刀
7 如图,以AB 边为直径的⊙O 经过点P,C 是 ⊙O上一点,连接PC 交AB 于点E,且∠ACP=60°,PA=PD.
(1)试判断PD 与⊙O 的位置关系,并说明理由;
(2)若点C 是弧AB 的中点,已知AB=4,求CE ·CP 的值.
小试牛刀
(1)试判断PD 与⊙O 的位置关系,并说明理由;
PD 与⊙O 相切.理由如下:
如图,连接OP.
∵∠ACP=60°,∴∠AOP=120°.
∵OA=OP,∴∠OAP=∠OPA=30°.
∵PA=PD,∴∠PAO=∠D=30°.
∴∠APD=120°.
∴∠OPD=∠APD-∠OPA=90°.
又∵OP 是⊙O 的半径,
∴PD 是⊙O 的切线.
解:
小试牛刀
解:
(2)若点C 是弧AB 的中点,已知AB=4,求CE · CP 的值.
如图,连接BC.
∵AB是⊙O 的直径,∴∠ACB=90°.
又∵C 为弧AB 的中点,
∴∠CAB=∠ABC=∠APC=45°.
∵AB=4,∴CA= AB=
∵∠ACE=∠PCA,∠CAB=∠APC,
∴△CAE∽△CPA.
∴ . ∴CE CP=CA 2=( )2=8.
小试牛刀
8 如图,已知Rt△ABC,∠C=90°,D 为BC 的中点,以AC 为直径的⊙O 交AB 于点E.
(1)求证:DE 是⊙O 的切线;
(2)若AE∶EB=1∶2,BC=6,求AE 的长.
小试牛刀
证明:
(1)求证:DE 是⊙O 的切线;
如图,连接OE,EC.
∵AC 是⊙O 的直径,
∴∠AEC=∠BEC=90°.
∵D 为BC 的中点,∴ED=DC=BD.
∴∠1=∠2.
∵OE=OC,∴∠3=∠4.
∴∠1+∠3=∠2+∠4,即∠OED=∠ACB.
∵∠ACB=90°,∴∠OED=90°.
∴DE 是⊙O 的切线.
小试牛刀
解:
(2)若AE∶EB=1∶2,BC=6,求AE 的长.
在△BEC 与△BCA 中,∠B=∠B,
∠BEC=∠BCA=90°,∴△BEC∽△BCA.
∴ ∴BC 2=BE BA.
由AE∶EB=1∶2,设AE=x,可得BE=2x,BA=3x.
∵BC=6,
∴62=2x 3x,解得x= (x=- 舍去),
即AE= .
课堂小结
课堂小结
判定两三角形相似的思路:
(1)平行于三角形一边的直线,找两个三角形;
(2)已知一角对应相等,找另一角对应相等,或夹这个角的两边成比例;
(3)已知两边对应成比例,找夹角相等,或与第三边成比例;
(4)已知等腰三角形,找顶角相等,或底角相等,或底、腰对应成比例.
(5)已知直角三角形,找一组锐角相等,或两直角边对应成比例,
或斜边、一直角边对应成比例.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.2 相似三角形
第5课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾:
三角形的内角和是多少度?
新课精讲
探索新知
1
知识点
两角分别相等的两个三角形相似
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺 , 相似吗?
探索新知
画一个三角形,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;
②这两个三角形相似吗
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角对应相等吗?
探索新知
相似三角形的判别方法1:
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似吗?
探索新知
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B '
∴ ΔABC ∽ ΔA'B 'C '
用数学符号表示:
相似三角形的判定
(两个角分别对应相等的两个三角形相似.)
探索新知
例1 如图,Rt△ABC 中,∠C=90°,AB=10,AC=8.E 是AC上
一 点,AE=5,ED⊥AB,垂足为D,求AD 的长.
解:∵ ED⊥AB,
∴ ∠EDA=90°.
又∠C=90 °, ∠A=∠A,
∴△AED∽△ABC.
A
D
B
C
E
探索新知
总 结
当两个三角形已具备一角对应相等的条件时,往往先找是否有另一角对应相等,当此思路不通时,再找夹等角的两边对应成比例.找角相等时应注意挖掘公共角、对顶角、同角的余角(或补角)等.
典题精讲
底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.
1
底角相等的两个等腰三角形相似.已知:在△ABC 中,AB=AC,在△A′B′C ′中,A′B ′=A′C ′,且∠B=∠B ′. 求证:△ABC∽△A′B′C ′.证明:在△ABC 中,∵AB=AC,∴∠B=∠C,同理∠B ′=∠C ′.又∵∠B=∠B ′,∴∠C=∠C ′. ∴△ABC∽△A′B′C ′. 顶角相等的两个等腰三角形相似.已知:在△ABC 中,AB=AC,在△A′B′C ′中,A′B ′=A′C ′,且∠A=∠A′.求证:△ABC∽△A′B′C ′.证明:在△ABC 中,∵AB=AC,∴∠B=∠C,同理∠B ′=∠C ′.又∵∠B= ∠B′=
∠A=∠A′,∴∠B=∠B ′.又∵∠A=∠A′,∴△ABC∽△A′B′C ′.
解:
典题精讲
2
下列各组条件中,不能判定△ABC 与△A′B′C′ 相似的是( )
A.∠A=∠A′,∠B=∠B′
B.∠C=∠C′=90°,∠A=35°,∠B′=55°
C.∠A=∠B,∠A′=∠B′
D.∠A+∠B=∠A′+∠B ′,∠A-∠B=∠A′-∠B ′
C
典题精讲
3
如图,△ABC 中,∠A=78°,AB=4,AC=6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
C
典题精讲
4
如图,△ABC 和△ADE 均为等边三角形,D 在BC 上,DE 与AC 相交于点F,AB=9,BD=3,则CF 等于( )
A.1
B.2
C.3
D.4
B
探索新知
2
知识点
两直角三角形相似的判定
思考:
我们知道,两个直角三角形全等可以用“HL”来判定.
那么,满足斜边和一条直角边成比例的两个直角三角形相似吗?
事实上,这两个直角三角形相似.下面我们给出证明.
如图,在Rt△ABC 和Rt△A′B′C′ 中, ∠C=90°,∠C′=90°,
求证: Rt△ABC∽Rt△A′B′C′ .
探索新知
分析:要证Rt△ABC∽Rt△A′B′C′ ,可设法证
∴Rt△ABC∽Rt△A′B′C′.
探索新知
归 纳
直角三角形相似的判定定理:
(1)有一锐角相等的两个直角三角形相似;
(2)有两组直角边对应成比例的两直角三角形相似.
数学表达式:
在Rt△ABC 和Rt△A′B′C′ 中,
(1)∵∠C=∠C′=90°,∠A=∠A′,∴Rt△ABC∽Rt△A′B′C ′;
(2)∵∠C=∠C′=90°,
∴Rt△ABC∽Rt△A′B′C ′.
探索新知
归 纳
直角三角形相似的判定方法:
有一锐角对应相等 两直角三角形相似
有两组直角边对应成比例 两直角三角形相似
有斜边与一直角边对应成比例 两直角三角形相似
探索新知
例2 在Rt△ABC 和Rt△DEF 中,∠C=∠F=90°,下列条
件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
导引:根据相似三角形的判定方法对各个选项进行分析即可.
A.∵∠A=55°,∴∠B=90°-55°=35°.
∵∠D=35°,∴∠B=∠D.
又∵∠C=∠F=90°,∴△ABC∽△EDF;
C
探索新知
B.∵AC=9,BC=12,DF=6,EF=8,
∴
又∵∠C=∠F=90°,∴△ABC∽△DEF;
C.由题目中知∠C=∠F=90°,但已知条件中不能得出两
组对应边成比例,故不能判定两三角形相似.
D.∵AB=10,AC=8,∴由勾股定理可得BC=6.
又DE=15,EF=9,∴
又∵∠C=∠F=90°,∴△ABC∽△DEF.
探索新知
总 结
判定两直角三角形相似的方法:
一个锐角对应相等,两组直角边对应成比例,斜边和一直角边对应成比例.
典题精讲
如图,Rt△ABC 中,CD 是斜边AB上的高.
求证:(1)△ACD∽△ABC; (2)△CBD∽△ABC.
1
(1)∵CD 是斜边AB上的高,∴∠ADC=90°.
在Rt△ABC 中,∠ACB=90°,
∴∠ADC=∠ACB.
又∵∠A=∠A,∴△ACD∽△ABC.
(2)∵CD 是斜边AB上的高,
∴∠CDB=90°.
在Rt△ABC 中,∠ACB=90°,
∴∠CDB=∠ACB.
又∵∠B=∠B,∴△CBD∽△ABC.
证明:
D
B
C
A
典题精讲
如果Rt△ABC 的两条直角边分别为3和4,那么以3k 和4k (k是正整数)为直角边的直角三角形一定与Rt△ABC 相似吗?为什么?
2
一定相似.理由如下:
∵两条对应直角边的比分别为
∴对应直角边的比相等.
又∵两直角边所夹的角都为直角,
∴两个三角形一定相似.
证明:
典题精讲
如图,矩形ABCD 中,AB=8,BC=4,点E 在AB上,点F 在CD上,点G,H 在对角线AC上,若四边形EGFH 是菱形,则AE 的长是( )
A.2 B.3 C.5 D.6
3
C
典题精讲
如图,正方形ABCD 中,M 为BC上一点,ME⊥AM,ME 交AD 的延长线于点E. 若AB=12,BM=5,则DE 的长为( )
A.18 B. C. D.
4
B
易错提醒
已知正方形ABCD 的边长为1,P 是CD 边的中点,Q 在线段BC上,△ADP 与△QCP 相似时,求BQ 的值.
解:
由题意,得∠D=∠C=90°.
①当 时,△ADP∽△PCQ,
即 ,得CQ= .故BQ=1- =
易错提醒
易错点: 相似情形考虑不全面,解答不完整.
跳出误区:因为题中∠D=∠C=90°,所以直角三角形相似在对应顺序上有两种可能,即△ADP∽△PCQ 或△ADP∽△QCP,此题容易因只考虑一种情况而漏解.
②当 时,△ADP∽△QCP,
即 ,得QC=1,故BQ=0.
所以当△ADP 与△QCP 相似时,BQ 的值为0或
学以致用
小试牛刀
1
如图,AB 是半圆O 的直径,D,E 是半圆上任意两点,连接AD,DE,AE 与BD 相交于点C,要使△ADC 与△ABD 相似,下列添加的条件错误的是( )
A.∠ACD=∠DAB
B.AD=DE
C.AD 2=BD·CD
D.CD·AB=AC·BD
D
小试牛刀
2
如图,在△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段AC 的长为( )
A.4
B.4
C.6
D.4
B
小试牛刀
3
如图,矩形ABCD 的边AD=3,AB=2,E 为AB 的中点,F 在边BC上,且BF=2FC,AF 分别与DE,DB 相交于点M,N,则MN 的长为( )
A.
B.
C.
D.
B
小试牛刀
如图,在△ABC 中,∠ACB=90°,CD⊥AB 于点D,下列结论中:
①AC·BC=AB·CD;②AC 2=AD·DB;③BC 2=BD·BA;④CD 2=AD·DB,正确的个数是( )
A.1
B.2
C.3
D.4
4
C
小试牛刀
5 如图,正方形ABCD 的顶点A 在等腰直角三角形DEF 的斜边EF上,EF 与BC 相交于点G,连接CF.
(1)求证:△DAE ≌ △DCF;
(2)求证:△ABG ∽ △CFG.
小试牛刀
在正方形ABCD、等腰直角三角形DEF 中,
∠ADC=∠EDF=90°,DA=DC,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF.
∴∠ADE=∠CDF.
在△ADE 和△CDF 中,
∴△ADE ≌ △CDF.
证明:
(1)求证:△DAE ≌ △DCF;
小试牛刀
如图,延长BA到M,交ED于点M.
∵△ADE ≌ △CDF,
∴∠EAD=∠FCD,即
∠EAM+∠MAD=∠BCF+∠BCD.
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF.
∵∠EAM=∠BAG,∴∠BAG=∠BCF.
∵∠AGB=∠CGF,∴△ABG∽△CFG.
证明:
(2)求证:△ABG∽△CFG.
小试牛刀
6 如图,AB 为半圆O 的直径,C 为BA 延长线上一点,CD 切半圆O于点D,连接OD. 作BE⊥CD 于点E,交半圆O 于点F. 已知CE=12,BE=9.
(1)求证:△COD ∽△CBE;
(2)求半圆O 的半径r 的长.
小试牛刀
∵CD 切半圆O 于点D,∴CD⊥OD,∴∠CDO=90°.
∵BE⊥CD,∴∠CDO=90°=∠E.
又∵∠C=∠C,∴△COD∽△CBE.
证明:
(1)求证:△COD∽△CBE;
解:
(2)求半圆O 的半径r 的长.
在Rt△BEC 中,CE=12,BE=9,
∴BC=
∵△COD∽△CBE,
∴ ,即 ,解得r=
小试牛刀
7 如图,以AB 边为直径的⊙O 经过点P,C 是 ⊙O上一点,连接PC 交AB 于点E,且∠ACP=60°,PA=PD.
(1)试判断PD 与⊙O 的位置关系,并说明理由;
(2)若点C 是弧AB 的中点,已知AB=4,求CE ·CP 的值.
小试牛刀
(1)试判断PD 与⊙O 的位置关系,并说明理由;
PD 与⊙O 相切.理由如下:
如图,连接OP.
∵∠ACP=60°,∴∠AOP=120°.
∵OA=OP,∴∠OAP=∠OPA=30°.
∵PA=PD,∴∠PAO=∠D=30°.
∴∠APD=120°.
∴∠OPD=∠APD-∠OPA=90°.
又∵OP 是⊙O 的半径,
∴PD 是⊙O 的切线.
解:
小试牛刀
解:
(2)若点C 是弧AB 的中点,已知AB=4,求CE · CP 的值.
如图,连接BC.
∵AB是⊙O 的直径,∴∠ACB=90°.
又∵C 为弧AB 的中点,
∴∠CAB=∠ABC=∠APC=45°.
∵AB=4,∴CA= AB=
∵∠ACE=∠PCA,∠CAB=∠APC,
∴△CAE∽△CPA.
∴ . ∴CE CP=CA 2=( )2=8.
小试牛刀
8 如图,已知Rt△ABC,∠C=90°,D 为BC 的中点,以AC 为直径的⊙O 交AB 于点E.
(1)求证:DE 是⊙O 的切线;
(2)若AE∶EB=1∶2,BC=6,求AE 的长.
小试牛刀
证明:
(1)求证:DE 是⊙O 的切线;
如图,连接OE,EC.
∵AC 是⊙O 的直径,
∴∠AEC=∠BEC=90°.
∵D 为BC 的中点,∴ED=DC=BD.
∴∠1=∠2.
∵OE=OC,∴∠3=∠4.
∴∠1+∠3=∠2+∠4,即∠OED=∠ACB.
∵∠ACB=90°,∴∠OED=90°.
∴DE 是⊙O 的切线.
小试牛刀
解:
(2)若AE∶EB=1∶2,BC=6,求AE 的长.
在△BEC 与△BCA 中,∠B=∠B,
∠BEC=∠BCA=90°,∴△BEC∽△BCA.
∴ ∴BC 2=BE BA.
由AE∶EB=1∶2,设AE=x,可得BE=2x,BA=3x.
∵BC=6,
∴62=2x 3x,解得x= (x=- 舍去),
即AE= .
课堂小结
课堂小结
判定两三角形相似的思路:
(1)平行于三角形一边的直线,找两个三角形;
(2)已知一角对应相等,找另一角对应相等,或夹这个角的两边成比例;
(3)已知两边对应成比例,找夹角相等,或与第三边成比例;
(4)已知等腰三角形,找顶角相等,或底角相等,或底、腰对应成比例.
(5)已知直角三角形,找一组锐角相等,或两直角边对应成比例,
或斜边、一直角边对应成比例.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
