【班海精品】人教版(新)九下-27.2 相似三角形 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-27.2 相似三角形 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览









文档简介
(共40张PPT)
27.2 相似三角形
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判定两个三角形全等我们有SSS 的方法,类似地,判定两个三角形相似是否也有类似的简单方法呢?
新课精讲
探索新知
1
知识点
三边成比例的两个三角形相似
任意画一个三角形,再画另一个三角形,使它的各边长都是原来各边长的2倍,度量这两个三角形的对应角,他们对应相等吗?这两个三角形全等吗?
问 题
探索新知
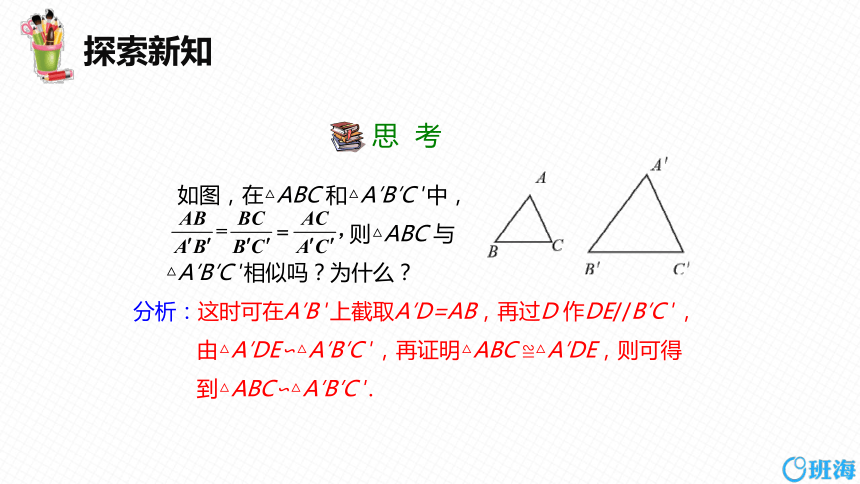
如图,在△ABC 和△A′B′C ′中,
则△ABC 与
△A′B′C ′相似吗?为什么?
分析:这时可在A′B ′上截取A′D=AB,再过D 作DE//B′C ′,由△A′DE∽△A′B′C ′,再证明△ABC ≌△A′DE,则可得到△ABC∽△A′B′C ′.
思 考
探索新知
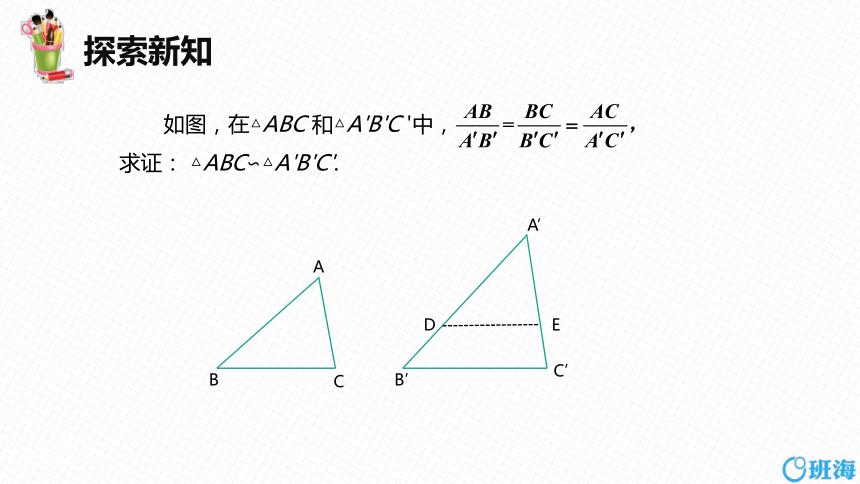
如图,在△ABC 和△A'B'C '中,
求证: △ABC∽△A'B'C'.
A
B
C
A’
C’
B’
D
E
探索新知
证明:在线段A′B ′(或它的延长线)上截取A′D=AB,过点D
作 DE//B′C ′,交A′C ′于点E.根据前面的定理,可得
△A′DE∽△A'B'C'.
∴DE=BC,A′E=AC.
∴ △A′DE ≌ △ABC.
∴△ABC ∽△A'B'C'.
△A′DE 是证明的中介,它把△ABC 与△A′B′C′ 联系起来.
探索新知
结 论
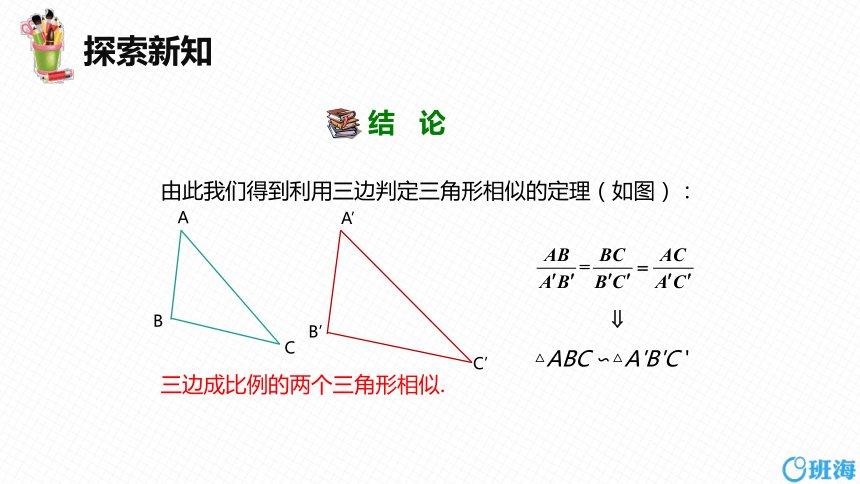
由此我们得到利用三边判定三角形相似的定理(如图):
三边成比例的两个三角形相似.
△ABC ∽△A'B'C '
A
B
C
A’
B’
C’
探索新知
例1 根据下列条件,判断△ABC 与△A'B'C' 是否相似,并说明理由:
AB=4 cm,BC=6 cm,AC=8 cm,
A′B ′= 12 cm,B′C ′= 18 cm,A′C ′=24 cm.
解:
∴△ABC ∽△A'B'C'.
探索新知
总 结
这个判定三角形相似的方法与三角形全等的判定方法“边边边”十分相似,所不同的是在相似的判定方法中的 “三边”要求的是“比相等”. 三边的对应关系是“短∶短”“中∶中”“长∶长”.
典题精讲
根据下列条件,判断△ABC 与△A′B′C ′是否相似,并说明理由:
AB= 10 cm,BC = 8 cm,AC = 16 cm,
A′B ′= 16 cm,B′C ′= 12. 8 cm,A′C ′= 25. 6 cm.
1
解:相似
∴△ABC∽△A′B′C ′.
典题精讲
图中的两个三角形是否相似?为什么?
2
相似
理由如下:∵
∴两个三角形的三边成比例.
∴这两个三角形相似.
解:
15
20
25
27
36
45
典题精讲
要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为 4 cm,5 cm和6 cm,另一个三角形框架的一边长为2 cm,它的另外两条边长应当是多少?你有几种制作方案?
3
设另外两条边长分别是x cm和y cm(x因此另外两条边长应当分别是 cm和3 cm或 cm和 cm或 cm和 cm,即有3种制作方案.
解:
典题精讲
4 若△ABC 和△A′B′C ′满足下列条件,其中使△ABC 与
△A′B′C′相似的是( )
A.AB=2.5 cm,BC=2 cm,AC=3 cm;A′B ′=3 cm,B′C ′=4 cm,A′C ′=6 cm
B.AB=2 cm,BC=3 cm,AC=4 cm;A′B ′=3 cm, B′C ′=6 cm,A′C ′= cm
C.AB=10 cm,BC=AC=8 cm;A′B ′= cm,B′C ′=A′C ′= cm
D.AB=1 cm,BC= cm,AC=3 cm;A′B ′= cm,B′C ′= cm,A′C ′= cm
B
典题精讲
要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4,5,6,另一个三角形框架的一边长为2,它的另外两边长分别可以为( )
A.2.5,3 B.
C.1.6,2.4 D.2.5,3或 或1.6,2.4
5
D
典题精讲
若△ABC 的每条边长增加各自的10%得△A′B′C ′,则∠B ′的度数与其对应角∠B 的度数相比( )
A.增加了10%
B.减少了10%
C.增加了(1+10%)
D.没有改变
6
D
探索新知
2
知识点
网格上相似三角形的判定
例2 图1,图2中小正方形的边长均为1,则图2中的哪一个三角形(阴影部分)与图1中的△ABC 相似?
导引:图中的三角形为格点三角形,可根据勾股定理求出各边的长,然后根据三角形三边的长度的比是否相等来判断哪两个三角形相似.
图1
图2
探索新知
解:由勾股定理知AC= ,BC=2,AB=
图2(1)中,三角形的三边长分别为1,
图2 (2)中,三角形的三边长分别为1,
图2 (3)中,三角形的三边长分别为
图2 (4)中,三角形的三边长分别为2,
∴图2 (2)中的三角形与△ABC 相似.
探索新知
总 结
利用三角形三边对应成比例判定两三角形相似的方法:
首先把两个三角形的边分别按照从小到大的顺序排列,找出两个三角形的对应边;再分别计算小、中、大边的比,最后看三个比是否相等,若相等,则两个三角形相似,否则不相似.特别地,若三个比相等且等于1,则两个三角形全等.
典题精讲
如图,4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC 相似的三角形所在的网格图形是( )
D
典题精讲
如图,若A,B,C,P,Q,甲,乙,丙,丁都是方格纸中的格点,为使△PQR∽△ABC,则点R 应是甲,乙,丙,丁四点中的( )
A.甲
B.乙
C.丙
D.丁
C
易错提醒
如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3,4及x,那么x 的值( )
A.只有1个 B.有2个
C.有3个 D.有无数个
B
易错点:易因考虑问题不全面而致错.
学以致用
小试牛刀
已知△ABC 的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当△DEF 的另两边是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm B.4 cm,5 cm
C.5 cm,6 cm D.6 cm,7 cm
1
C
一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边的长是21,则其他两边长的和是( )
A.19 B.17
C.24 D.21
2
C
小试牛刀
如图,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK. ②~⑥中与①相似的是( )
A.②③④
B.③④⑤
C.④⑤⑥
D.②③⑥
B
小试牛刀
4 如图, ,求证:∠BAD=∠CAE.
证明:
∵
∴△ABC∽△ADE.
∴∠BAC=∠DAE.
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠BAD=∠CAE.
小试牛刀
5 如图所示,在正方形ABCD 中,P 是BC 上一点,且BP=3PC,Q 是CD 的中点,求证:△ADQ∽△QCP.
小试牛刀
证明:
设正方形ABCD 的边长为a.
∵Q 是CD 的中点,∴DQ=CQ= a.
∵BP=3PC,∴PC= a,
∴AQ=
PQ=
∴
∴△ADQ∽△QCP.
小试牛刀
6 如图,四边形ABCD,CDEF,EFGH 都是相同的正方形.
(1)△ACF 与△GCA 相似吗 说说你的理由.
(2)求∠1+∠2的度数.
小试牛刀
解:
(1)△ACF 与△GCA 相似吗 说说你的理由.
△ACF∽△GCA.理由:可设正方形ABCD,CDEF,
EFGH 的边长为a,则△ACF 的三边长分别为:
AC= ,CF=a,AF= ,
△ACG 的三边长分别为:
AC= ,CG=2a,AG= .
∴
∴ ∴△ACF 与△GCA 相似.
小试牛刀
解:
∵△ACF∽△GCA,
∴∠1=∠CAF,
∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
(2)求∠1+∠2的度数.
小试牛刀
7 如图,在边长为1的小正方形组成的网格中,△ABC 和△DEF 的顶点都在格点上,P1,P2,P3,P4,P5是△DEF 边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC 为直角三角形;
(2)判断△ABC 和△DEF 是否相似,并说明理由;
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中
的3个格点并且与△ABC 相似,并予以证明.
小试牛刀
证明:
(1)试证明△ABC 为直角三角形;
根据勾股定理,得AB= ,AC= ,BC=5,
显然有AB 2+AC 2=BC 2,
根据勾股定理的逆定理得△ABC 为直角三角形.
小试牛刀
解:
(2)判断△ABC 和△DEF 是否相似,并说明理由;
△ABC 和△DEF 相似.理由如下:
在△DEF 中根据勾股定理,得
DE= ,DF= ,EF= .
又∵AB= ,AC= ,BC=5,
∴
∴△ABC∽△DEF.
小试牛刀
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,
P5中的3个格点并且与△ABC 相似,并予以证明.
解:
如图,连接P2P5,P2P4,P4P5,则△P2P4P5符合要求.
证明:∵P2P5= ,P2P4= ,P4P5= ,
AB= ,AC= ,BC=5,
∴
∴△ABC∽△P4P5P2.
课堂小结
课堂小结
利用三边成比例判定三角形相似的“三步骤”:
(1)排序:将三角形的边按大小顺序排列;
(2)计算:分别计算它们对应边的比值;
(3)判断:通过比值是否相等判断两个三角形是否相似.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.2 相似三角形
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判定两个三角形全等我们有SSS 的方法,类似地,判定两个三角形相似是否也有类似的简单方法呢?
新课精讲
探索新知
1
知识点
三边成比例的两个三角形相似
任意画一个三角形,再画另一个三角形,使它的各边长都是原来各边长的2倍,度量这两个三角形的对应角,他们对应相等吗?这两个三角形全等吗?
问 题
探索新知
如图,在△ABC 和△A′B′C ′中,
则△ABC 与
△A′B′C ′相似吗?为什么?
分析:这时可在A′B ′上截取A′D=AB,再过D 作DE//B′C ′,由△A′DE∽△A′B′C ′,再证明△ABC ≌△A′DE,则可得到△ABC∽△A′B′C ′.
思 考
探索新知
如图,在△ABC 和△A'B'C '中,
求证: △ABC∽△A'B'C'.
A
B
C
A’
C’
B’
D
E
探索新知
证明:在线段A′B ′(或它的延长线)上截取A′D=AB,过点D
作 DE//B′C ′,交A′C ′于点E.根据前面的定理,可得
△A′DE∽△A'B'C'.
∴DE=BC,A′E=AC.
∴ △A′DE ≌ △ABC.
∴△ABC ∽△A'B'C'.
△A′DE 是证明的中介,它把△ABC 与△A′B′C′ 联系起来.
探索新知
结 论
由此我们得到利用三边判定三角形相似的定理(如图):
三边成比例的两个三角形相似.
△ABC ∽△A'B'C '
A
B
C
A’
B’
C’
探索新知
例1 根据下列条件,判断△ABC 与△A'B'C' 是否相似,并说明理由:
AB=4 cm,BC=6 cm,AC=8 cm,
A′B ′= 12 cm,B′C ′= 18 cm,A′C ′=24 cm.
解:
∴△ABC ∽△A'B'C'.
探索新知
总 结
这个判定三角形相似的方法与三角形全等的判定方法“边边边”十分相似,所不同的是在相似的判定方法中的 “三边”要求的是“比相等”. 三边的对应关系是“短∶短”“中∶中”“长∶长”.
典题精讲
根据下列条件,判断△ABC 与△A′B′C ′是否相似,并说明理由:
AB= 10 cm,BC = 8 cm,AC = 16 cm,
A′B ′= 16 cm,B′C ′= 12. 8 cm,A′C ′= 25. 6 cm.
1
解:相似
∴△ABC∽△A′B′C ′.
典题精讲
图中的两个三角形是否相似?为什么?
2
相似
理由如下:∵
∴两个三角形的三边成比例.
∴这两个三角形相似.
解:
15
20
25
27
36
45
典题精讲
要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为 4 cm,5 cm和6 cm,另一个三角形框架的一边长为2 cm,它的另外两条边长应当是多少?你有几种制作方案?
3
设另外两条边长分别是x cm和y cm(x
解:
典题精讲
4 若△ABC 和△A′B′C ′满足下列条件,其中使△ABC 与
△A′B′C′相似的是( )
A.AB=2.5 cm,BC=2 cm,AC=3 cm;A′B ′=3 cm,B′C ′=4 cm,A′C ′=6 cm
B.AB=2 cm,BC=3 cm,AC=4 cm;A′B ′=3 cm, B′C ′=6 cm,A′C ′= cm
C.AB=10 cm,BC=AC=8 cm;A′B ′= cm,B′C ′=A′C ′= cm
D.AB=1 cm,BC= cm,AC=3 cm;A′B ′= cm,B′C ′= cm,A′C ′= cm
B
典题精讲
要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4,5,6,另一个三角形框架的一边长为2,它的另外两边长分别可以为( )
A.2.5,3 B.
C.1.6,2.4 D.2.5,3或 或1.6,2.4
5
D
典题精讲
若△ABC 的每条边长增加各自的10%得△A′B′C ′,则∠B ′的度数与其对应角∠B 的度数相比( )
A.增加了10%
B.减少了10%
C.增加了(1+10%)
D.没有改变
6
D
探索新知
2
知识点
网格上相似三角形的判定
例2 图1,图2中小正方形的边长均为1,则图2中的哪一个三角形(阴影部分)与图1中的△ABC 相似?
导引:图中的三角形为格点三角形,可根据勾股定理求出各边的长,然后根据三角形三边的长度的比是否相等来判断哪两个三角形相似.
图1
图2
探索新知
解:由勾股定理知AC= ,BC=2,AB=
图2(1)中,三角形的三边长分别为1,
图2 (2)中,三角形的三边长分别为1,
图2 (3)中,三角形的三边长分别为
图2 (4)中,三角形的三边长分别为2,
∴图2 (2)中的三角形与△ABC 相似.
探索新知
总 结
利用三角形三边对应成比例判定两三角形相似的方法:
首先把两个三角形的边分别按照从小到大的顺序排列,找出两个三角形的对应边;再分别计算小、中、大边的比,最后看三个比是否相等,若相等,则两个三角形相似,否则不相似.特别地,若三个比相等且等于1,则两个三角形全等.
典题精讲
如图,4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC 相似的三角形所在的网格图形是( )
D
典题精讲
如图,若A,B,C,P,Q,甲,乙,丙,丁都是方格纸中的格点,为使△PQR∽△ABC,则点R 应是甲,乙,丙,丁四点中的( )
A.甲
B.乙
C.丙
D.丁
C
易错提醒
如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3,4及x,那么x 的值( )
A.只有1个 B.有2个
C.有3个 D.有无数个
B
易错点:易因考虑问题不全面而致错.
学以致用
小试牛刀
已知△ABC 的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当△DEF 的另两边是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm B.4 cm,5 cm
C.5 cm,6 cm D.6 cm,7 cm
1
C
一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边的长是21,则其他两边长的和是( )
A.19 B.17
C.24 D.21
2
C
小试牛刀
如图,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK. ②~⑥中与①相似的是( )
A.②③④
B.③④⑤
C.④⑤⑥
D.②③⑥
B
小试牛刀
4 如图, ,求证:∠BAD=∠CAE.
证明:
∵
∴△ABC∽△ADE.
∴∠BAC=∠DAE.
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠BAD=∠CAE.
小试牛刀
5 如图所示,在正方形ABCD 中,P 是BC 上一点,且BP=3PC,Q 是CD 的中点,求证:△ADQ∽△QCP.
小试牛刀
证明:
设正方形ABCD 的边长为a.
∵Q 是CD 的中点,∴DQ=CQ= a.
∵BP=3PC,∴PC= a,
∴AQ=
PQ=
∴
∴△ADQ∽△QCP.
小试牛刀
6 如图,四边形ABCD,CDEF,EFGH 都是相同的正方形.
(1)△ACF 与△GCA 相似吗 说说你的理由.
(2)求∠1+∠2的度数.
小试牛刀
解:
(1)△ACF 与△GCA 相似吗 说说你的理由.
△ACF∽△GCA.理由:可设正方形ABCD,CDEF,
EFGH 的边长为a,则△ACF 的三边长分别为:
AC= ,CF=a,AF= ,
△ACG 的三边长分别为:
AC= ,CG=2a,AG= .
∴
∴ ∴△ACF 与△GCA 相似.
小试牛刀
解:
∵△ACF∽△GCA,
∴∠1=∠CAF,
∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
(2)求∠1+∠2的度数.
小试牛刀
7 如图,在边长为1的小正方形组成的网格中,△ABC 和△DEF 的顶点都在格点上,P1,P2,P3,P4,P5是△DEF 边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC 为直角三角形;
(2)判断△ABC 和△DEF 是否相似,并说明理由;
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中
的3个格点并且与△ABC 相似,并予以证明.
小试牛刀
证明:
(1)试证明△ABC 为直角三角形;
根据勾股定理,得AB= ,AC= ,BC=5,
显然有AB 2+AC 2=BC 2,
根据勾股定理的逆定理得△ABC 为直角三角形.
小试牛刀
解:
(2)判断△ABC 和△DEF 是否相似,并说明理由;
△ABC 和△DEF 相似.理由如下:
在△DEF 中根据勾股定理,得
DE= ,DF= ,EF= .
又∵AB= ,AC= ,BC=5,
∴
∴△ABC∽△DEF.
小试牛刀
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,
P5中的3个格点并且与△ABC 相似,并予以证明.
解:
如图,连接P2P5,P2P4,P4P5,则△P2P4P5符合要求.
证明:∵P2P5= ,P2P4= ,P4P5= ,
AB= ,AC= ,BC=5,
∴
∴△ABC∽△P4P5P2.
课堂小结
课堂小结
利用三边成比例判定三角形相似的“三步骤”:
(1)排序:将三角形的边按大小顺序排列;
(2)计算:分别计算它们对应边的比值;
(3)判断:通过比值是否相等判断两个三角形是否相似.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
