【班海精品】人教版(新)九下-27.2 相似三角形 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-27.2 相似三角形 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
27.2 相似三角形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、什么叫相似多边形呢?
2、你能类似的给相似三角形下一个定义吗?
3、什么叫相似比?
复习回顾:
新课精讲
探索新知
1
知识点
相似三角形
1. 各角对应相等,各边对应成比例的两个多边形叫相似多边形。
2. 三个角对应相等,三条边对应成比例的两个三角形叫相似三角形。
相似三角形对应边的比,叫做相似比.
探索新知
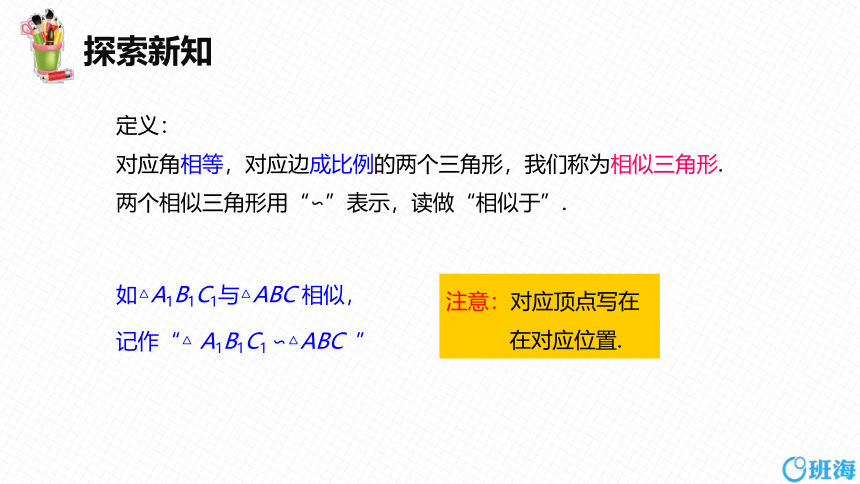
定义:
对应角相等,对应边成比例的两个三角形,我们称为相似三角形.
两个相似三角形用“∽”表示,读做“相似于”.
如△A1B1C1与△ABC 相似,
注意:对应顶点写在
在对应位置.
记作“△ A1B1C1 ∽△ABC ”
探索新知
∠A=∠A1、∠B=∠B1、∠C=∠C1
用数学语言表示:(符号)
△ABC∽△A1B1C1
}
探索新知
例1 如图所示,△ABC∽△DEF,其中AB=6,DE=9,
指出对应边、对应角,
并求出相似比.
导引:用“∽”表示两个图形相似时,表示对应顶点的
字母应该写在对应的位置上.
解:对应边分别是:AB 与DE,BC 与EF,AC 与DF.
对应角分别是:∠A与∠D,∠B 与∠E,∠C 与∠F.
∵AB∶DE=6∶9=2∶3,∴相似比为2∶3.
探索新知
总 结
(1)对应性:表示两三角形相似时,要注意对应性,即要把对应顶点写在对应位置上.
(2)顺序性:求两相似三角形的相似比,要注意顺序性.若当△ABC∽△A′B′C ′时,
则△A′B′C ′∽△ABC 时,
探索新知
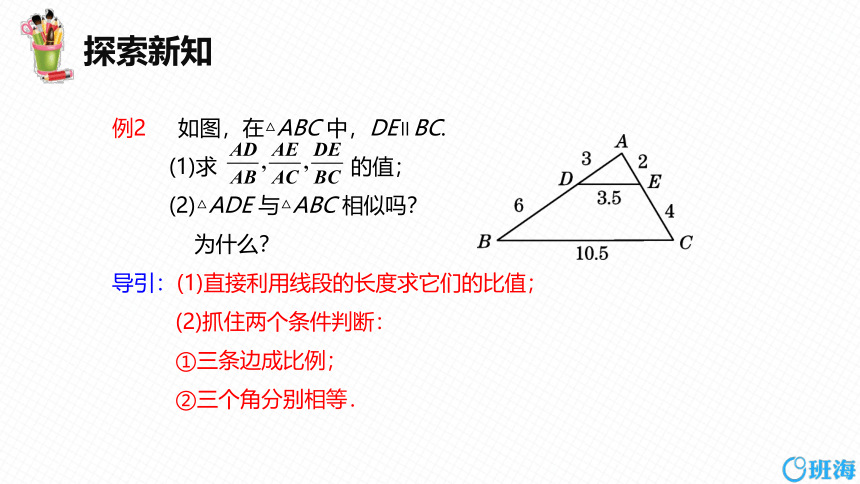
例2 如图,在△ABC 中,DE∥BC.
(1)求 的值;
(2)△ADE 与△ABC 相似吗?
为什么?
导引:(1)直接利用线段的长度求它们的比值;
(2)抓住两个条件判断:
①三条边成比例;
②三个角分别相等.
探索新知
解:(1)由图形可知AB=9,AC=6.
(2)△ADE 与△ABC 相似.理由如下:
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB.
由(1)知
又∵∠DAE=∠BAC,
∴△ADE∽△ABC.
探索新知
总 结
由于三角形是最简单的多边形,因此判定两个三角形相似可以根据判定两个多边形相似的方法,即利用相似三角形的定义证出三个角分别相等,三条边成比例即可.
典题精讲
1 如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C 等于( )
A.40°
B.60°
C.80°
D.100°
C
典题精讲
如图,△ABC∽△DEF,相似比为1∶2. 若BC =1,则EF 的长是( )
A.1 B.2
C.3 D.4
B
探索新知
2
知识点
平行线分线段成比例的基本事实
如果一组平行线在一条直线上截得的线段相等,
那么在其他直线上截得的线段也相等.
A
B
C
A1
B1
C1
l1
l3
l2
符号语言
∵直线l1∥l2∥l3 ,AB=BC
∴ A1B1=B1C1
?
?
探索新知
几何语言
∵ l1 //l 2// l3
(平行线分线段成比例)
两条直线被一组平行线所截,所得的对应线段成比例.
结论
D
E
F
A
B
C
l1
l2
l3
l4
l5
∴
探索新知
例3 如图,已知AB∥CD∥EF,AF 交BE 于点H,下列结论中错误的是( )
A. B.
C. D.
导引:本题中利用平行线分线段成比例的基本事实
的图形主要有“A”型和“X”型,从每种图形
中找出比例线段即可判断.
C
探索新知
解析:根据AB∥CD∥EF,结合平行线分线段成比例的本事实可得解.
∵AB∥CD∥EF,
故选项A,B,D正确.
∵CD∥EF,∴ 故选项C 错误.
探索新知
总 结
在题目中如遇到与直线平行相关的问题时,可从两个方面得到信息:一是位置角之间的关系(同位角相等、内错角相等、同旁内角互补);二是线段之间的关系,即平行线分线段成比例.
典题精讲
如图,已知直线a∥b∥c,直线m 分别交直线a,b,c 于点A,B,C,直线n 分别交直线a,b,c 于点D,E,F. 若 则 等于( )
A.
B.
C.
D. 1
1
B
典题精讲
如图,AB∥CD∥EF,AF 与BE 相交于点G,且AG=2,GD=1,DF=5,那么 =______.
2
探索新知
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
数学表达式:
如图,∵DE∥BC,
3
知识点
平行线分线段成比例基本事实的推论
探索新知
例4 如图,F 是 ABCD 的边CD上一点,连接BF,并延长BF 交AD 的延长线于点E. 求证:
解析:先根据平行四边形的性质得出AD∥BC,AB∥CD,再根据平行线分线段成比例定理的推论得出对应边成比例即可得出结论.
探索新知
证明:∵四边形ABCD 是平行四边形,
∴CD∥AB,AD∥BC.
(平行于三角形一边的直线截其他两
边,所得的对应线段成比例).
同理可得
探索新知
总 结
本题是证明等积式的典型题.要证明 经常要把它转化为两个等式: 我们通常把 叫做中间比.而找中间比的常见的方法就是通过找到平行线,然后利用平行线分线段成比例定理和它的推论来构造比例式.
典题精讲
如图,在△ABC中,DE∥BC,若 则 等于( )
A. B. C. D.
1
C
典题精讲
如图,在△ABC 中,FG∥DE∥BC,已知DF=3,AG=EC=2,
则下列四个等式中一定正确的是( )
A.FG·DE=6
B.DB·GE=6
C.FG:DE=2:3
D.CE:DB=3:2
2
B
易错提醒
如图,在△ABC 中,DE∥BC,以下结论正确的是( )
A. B.
C. D.
C
易错点:运用平行线分线段成比例的基本事实的推论时找不准对应关系.
学以致用
小试牛刀
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C 都在横格线上.若线段AB=4 cm,则线段BC=________.
1
12cm
小试牛刀
如图,在△ABC 中,若DE∥BC,EF∥AB,则下列比例式正确
的是( )
A.
B.
C.
D.
2
C
小试牛刀
如图,在△ABC 中,点D 为AC 上一点,且 过点D
作DE∥BC 交AB 于点 E,连接CE,过点D 作DF∥CE 交AB 于
点F. 若AB=15,则EF=________.
3
小试牛刀
4 如图,在△ABC 中,点D,E,F 分别在边AB,BC,CA上,DE∥AC,DF∥BC.如果BE=6 cm,EC=10 cm,FA-FC=3 cm,求FC 的长.
小试牛刀
解:
∵DE∥AC,BE=6 cm,EC=10 cm,
∴
又∵DF∥BC,
∴
而FA-FC=3 cm,∴FA=FC+3 cm.
∴
∴CF=4.5 cm.
5 如图,E 为 ABCD 的边CD 的延长线上一点,连接BE,交AC 于O,交AD 于F.
求证:BO 2=OF ·OE.
小试牛刀
证明:
∵四边形ABCD 是平行四边形,
∴AB∥CD,AD∥BC.
∴
∴
即BO 2=OF OE.
小试牛刀
6 如图,在△ABC 中,AD 是BC 边上的中线,M 是AD 的中点,BM 的延长线交AC 于N.
求证:AN= CN.
证明:
如图,过点D 作DE∥BN,交AC 于点E.
∵AD 是BC 边上的中线,
∴BD=DC. 又∵DE∥BN,∴CE=NE.
又∵M 是AD 的中点,DE∥MN,
∴AN=NE. ∴AN=NE=CE.
又∵CN=NE+CE=2AN,∴AN= CN.
E
小试牛刀
7 三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比.
已知:如图,在△ABC中,AD 是角平分线.
求证:
小试牛刀
解:
如图,过点C 作CE∥DA,交BA 的延长线于点E.
∴∠1=∠E,∠2=∠3.
∵AD 是△ABC 的角平分线,
∴∠1=∠2.
∴∠3=∠E.
∴AC=AE.
又∵AD∥CE,
∴ ∴
课堂小结
课堂小结
平行线除了具备造成“三线八角”相等或互补的功能外,还可以分线段成比例,而利用平行线得线段成比例的基本思路是:
(1)善于从较复杂的几何图形中分离出基本图形:
“ 型”或“ 型”,得到相应的比例式;
(2)平行是前提条件,没有平行线可以添加辅助线,
一般从分点或中点出发作平行线.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.2 相似三角形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、什么叫相似多边形呢?
2、你能类似的给相似三角形下一个定义吗?
3、什么叫相似比?
复习回顾:
新课精讲
探索新知
1
知识点
相似三角形
1. 各角对应相等,各边对应成比例的两个多边形叫相似多边形。
2. 三个角对应相等,三条边对应成比例的两个三角形叫相似三角形。
相似三角形对应边的比,叫做相似比.
探索新知
定义:
对应角相等,对应边成比例的两个三角形,我们称为相似三角形.
两个相似三角形用“∽”表示,读做“相似于”.
如△A1B1C1与△ABC 相似,
注意:对应顶点写在
在对应位置.
记作“△ A1B1C1 ∽△ABC ”
探索新知
∠A=∠A1、∠B=∠B1、∠C=∠C1
用数学语言表示:(符号)
△ABC∽△A1B1C1
}
探索新知
例1 如图所示,△ABC∽△DEF,其中AB=6,DE=9,
指出对应边、对应角,
并求出相似比.
导引:用“∽”表示两个图形相似时,表示对应顶点的
字母应该写在对应的位置上.
解:对应边分别是:AB 与DE,BC 与EF,AC 与DF.
对应角分别是:∠A与∠D,∠B 与∠E,∠C 与∠F.
∵AB∶DE=6∶9=2∶3,∴相似比为2∶3.
探索新知
总 结
(1)对应性:表示两三角形相似时,要注意对应性,即要把对应顶点写在对应位置上.
(2)顺序性:求两相似三角形的相似比,要注意顺序性.若当△ABC∽△A′B′C ′时,
则△A′B′C ′∽△ABC 时,
探索新知
例2 如图,在△ABC 中,DE∥BC.
(1)求 的值;
(2)△ADE 与△ABC 相似吗?
为什么?
导引:(1)直接利用线段的长度求它们的比值;
(2)抓住两个条件判断:
①三条边成比例;
②三个角分别相等.
探索新知
解:(1)由图形可知AB=9,AC=6.
(2)△ADE 与△ABC 相似.理由如下:
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB.
由(1)知
又∵∠DAE=∠BAC,
∴△ADE∽△ABC.
探索新知
总 结
由于三角形是最简单的多边形,因此判定两个三角形相似可以根据判定两个多边形相似的方法,即利用相似三角形的定义证出三个角分别相等,三条边成比例即可.
典题精讲
1 如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C 等于( )
A.40°
B.60°
C.80°
D.100°
C
典题精讲
如图,△ABC∽△DEF,相似比为1∶2. 若BC =1,则EF 的长是( )
A.1 B.2
C.3 D.4
B
探索新知
2
知识点
平行线分线段成比例的基本事实
如果一组平行线在一条直线上截得的线段相等,
那么在其他直线上截得的线段也相等.
A
B
C
A1
B1
C1
l1
l3
l2
符号语言
∵直线l1∥l2∥l3 ,AB=BC
∴ A1B1=B1C1
?
?
探索新知
几何语言
∵ l1 //l 2// l3
(平行线分线段成比例)
两条直线被一组平行线所截,所得的对应线段成比例.
结论
D
E
F
A
B
C
l1
l2
l3
l4
l5
∴
探索新知
例3 如图,已知AB∥CD∥EF,AF 交BE 于点H,下列结论中错误的是( )
A. B.
C. D.
导引:本题中利用平行线分线段成比例的基本事实
的图形主要有“A”型和“X”型,从每种图形
中找出比例线段即可判断.
C
探索新知
解析:根据AB∥CD∥EF,结合平行线分线段成比例的本事实可得解.
∵AB∥CD∥EF,
故选项A,B,D正确.
∵CD∥EF,∴ 故选项C 错误.
探索新知
总 结
在题目中如遇到与直线平行相关的问题时,可从两个方面得到信息:一是位置角之间的关系(同位角相等、内错角相等、同旁内角互补);二是线段之间的关系,即平行线分线段成比例.
典题精讲
如图,已知直线a∥b∥c,直线m 分别交直线a,b,c 于点A,B,C,直线n 分别交直线a,b,c 于点D,E,F. 若 则 等于( )
A.
B.
C.
D. 1
1
B
典题精讲
如图,AB∥CD∥EF,AF 与BE 相交于点G,且AG=2,GD=1,DF=5,那么 =______.
2
探索新知
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
数学表达式:
如图,∵DE∥BC,
3
知识点
平行线分线段成比例基本事实的推论
探索新知
例4 如图,F 是 ABCD 的边CD上一点,连接BF,并延长BF 交AD 的延长线于点E. 求证:
解析:先根据平行四边形的性质得出AD∥BC,AB∥CD,再根据平行线分线段成比例定理的推论得出对应边成比例即可得出结论.
探索新知
证明:∵四边形ABCD 是平行四边形,
∴CD∥AB,AD∥BC.
(平行于三角形一边的直线截其他两
边,所得的对应线段成比例).
同理可得
探索新知
总 结
本题是证明等积式的典型题.要证明 经常要把它转化为两个等式: 我们通常把 叫做中间比.而找中间比的常见的方法就是通过找到平行线,然后利用平行线分线段成比例定理和它的推论来构造比例式.
典题精讲
如图,在△ABC中,DE∥BC,若 则 等于( )
A. B. C. D.
1
C
典题精讲
如图,在△ABC 中,FG∥DE∥BC,已知DF=3,AG=EC=2,
则下列四个等式中一定正确的是( )
A.FG·DE=6
B.DB·GE=6
C.FG:DE=2:3
D.CE:DB=3:2
2
B
易错提醒
如图,在△ABC 中,DE∥BC,以下结论正确的是( )
A. B.
C. D.
C
易错点:运用平行线分线段成比例的基本事实的推论时找不准对应关系.
学以致用
小试牛刀
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C 都在横格线上.若线段AB=4 cm,则线段BC=________.
1
12cm
小试牛刀
如图,在△ABC 中,若DE∥BC,EF∥AB,则下列比例式正确
的是( )
A.
B.
C.
D.
2
C
小试牛刀
如图,在△ABC 中,点D 为AC 上一点,且 过点D
作DE∥BC 交AB 于点 E,连接CE,过点D 作DF∥CE 交AB 于
点F. 若AB=15,则EF=________.
3
小试牛刀
4 如图,在△ABC 中,点D,E,F 分别在边AB,BC,CA上,DE∥AC,DF∥BC.如果BE=6 cm,EC=10 cm,FA-FC=3 cm,求FC 的长.
小试牛刀
解:
∵DE∥AC,BE=6 cm,EC=10 cm,
∴
又∵DF∥BC,
∴
而FA-FC=3 cm,∴FA=FC+3 cm.
∴
∴CF=4.5 cm.
5 如图,E 为 ABCD 的边CD 的延长线上一点,连接BE,交AC 于O,交AD 于F.
求证:BO 2=OF ·OE.
小试牛刀
证明:
∵四边形ABCD 是平行四边形,
∴AB∥CD,AD∥BC.
∴
∴
即BO 2=OF OE.
小试牛刀
6 如图,在△ABC 中,AD 是BC 边上的中线,M 是AD 的中点,BM 的延长线交AC 于N.
求证:AN= CN.
证明:
如图,过点D 作DE∥BN,交AC 于点E.
∵AD 是BC 边上的中线,
∴BD=DC. 又∵DE∥BN,∴CE=NE.
又∵M 是AD 的中点,DE∥MN,
∴AN=NE. ∴AN=NE=CE.
又∵CN=NE+CE=2AN,∴AN= CN.
E
小试牛刀
7 三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比.
已知:如图,在△ABC中,AD 是角平分线.
求证:
小试牛刀
解:
如图,过点C 作CE∥DA,交BA 的延长线于点E.
∴∠1=∠E,∠2=∠3.
∵AD 是△ABC 的角平分线,
∴∠1=∠2.
∴∠3=∠E.
∴AC=AE.
又∵AD∥CE,
∴ ∴
课堂小结
课堂小结
平行线除了具备造成“三线八角”相等或互补的功能外,还可以分线段成比例,而利用平行线得线段成比例的基本思路是:
(1)善于从较复杂的几何图形中分离出基本图形:
“ 型”或“ 型”,得到相应的比例式;
(2)平行是前提条件,没有平行线可以添加辅助线,
一般从分点或中点出发作平行线.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
