【班海精品】人教版(新)九下-27.3 位似 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-27.3 位似 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览









文档简介
(共47张PPT)
27.3 位似
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在幻灯机放映图片的过程中,这些图片有什么关系呢?
幻灯机在哪儿呢?
放幻灯片
A’
B’
D’
C’
A
B
D
C
新课精讲
探索新知
1
知识点
位似图形的认识
这两个图形有哪些特征呢?
1.两图形相似;
2.每组对应点所在直线都经过同一点;
3. 对应边互相平行.
探索新知
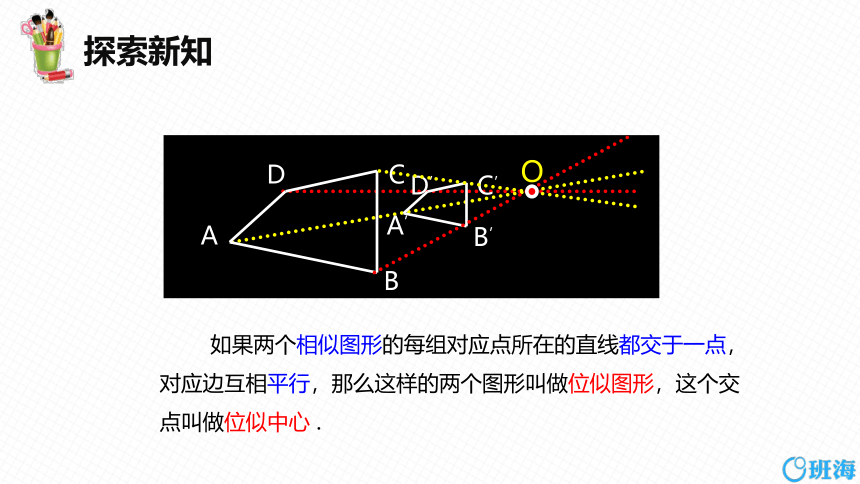
如果两个相似图形的每组对应点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个交点叫做位似中心 .
如果两个
A
B
D
C
A’
B’
D’
C’
O
探索新知
1.两图形相似;
同时满足下面三个条件的两个图形才叫做位似图形.三条件缺一不可.
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
2.每组对应点所在直线都经过同一点;
3. 对应边互相平行.
探索新知
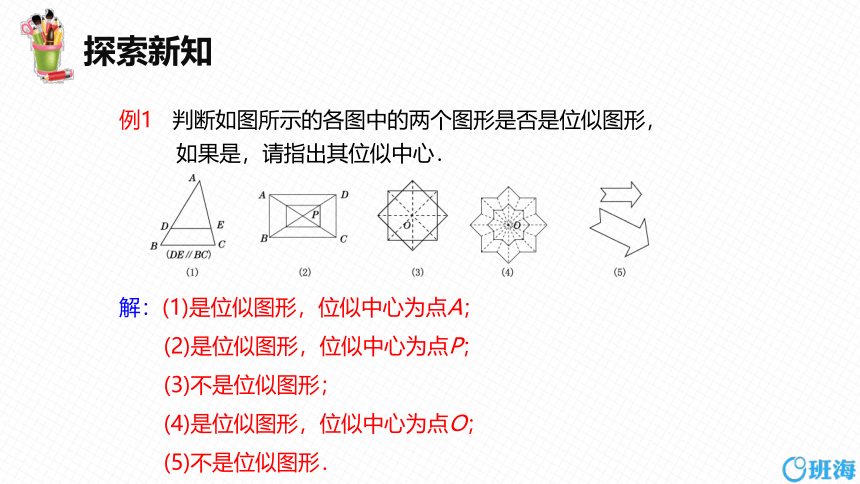
例1 判断如图所示的各图中的两个图形是否是位似图形,
如果是,请指出其位似中心.
解:(1)是位似图形,位似中心为点A;
(2)是位似图形,位似中心为点P;
(3)不是位似图形;
(4)是位似图形,位似中心为点O;
(5)不是位似图形.
典题精讲
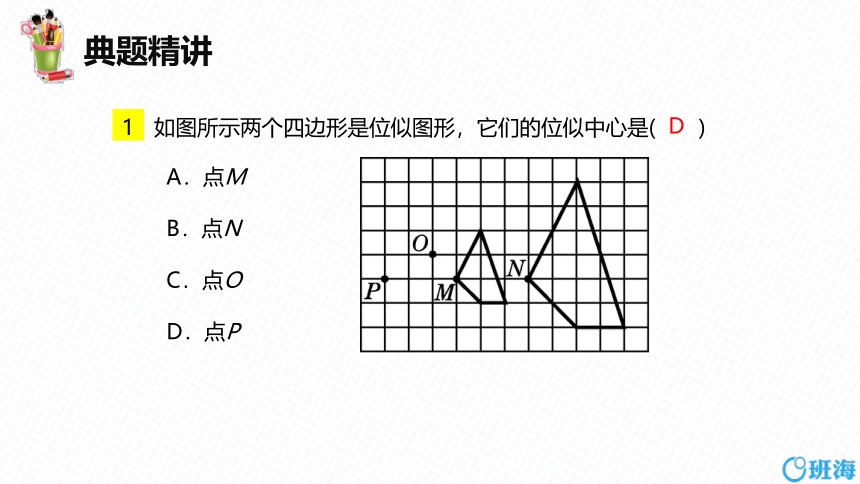
如图所示两个四边形是位似图形,它们的位似中心是( )
A.点M
B.点N
C.点O
D.点P
D
典题精讲
对于平面图形上的任意两点P,Q,如果经过某种变换得到新图形上的对应点P ′,Q ′,保持PQ=P′Q ′,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是( )
A.平移 B.旋转
C.轴对称 D.位似
2
D
典题精讲
利用位似图形将一个图形放大或缩小时,首先要选取一点作为位似中心,那么位似中心可以在( )
A.图形外 B.图形内
C.图形上 D.以上都可以
3
D
探索新知
2
知识点
位似图形的性质
图中有多边形相似吗?如果有,那么这种相似有什么特征?
C
B
B’
C’
O
A’
A
A
B
D
C
E
F
P
探索新知
位似图形上任意一对对应点到位似中心的距离之比等于位似比.
1. 位似图形的对应点和位似中心在同一条直线上;
位似图形有以下性质:
探索新知
例2 △ABC 与△A′B ′C ′是位似图形,且△ABC 与△A′B ′C ′的位似比
是1∶2,已知△ABC 的面积是3,则△A′B ′C ′的面积是( )
A. 3 B. 6 C. 9 D. 12
导引:∵△ABC 与△A′B ′C ′是位似图形,且△ABC 与
△A′B ′C ′的位似比是1∶2,
∴△ABC 与△A′B ′C ′相似,且相似比为1∶2.
∴△ABC 与△A′B ′C ′的面积比为1∶4.
∵△ABC 的面积是3,∴△A′B ′C ′的面积是12.
D
探索新知
总 结
两个图形位似,则两个图形相似,所以相似图形的性质,位似图形都满足,可以直接运用.
典题精讲
如图,△OAB 和△OCD 是位似图形,AB 与CD 平行吗?为什么?
解:AB∥CD. 理由如下:
∵△OAB 和△OCD 是位似图形,
∴△OAB∽△OCD.
∴∠OAB=∠C.
∴AB∥CD.
A
B
O
D
C
典题精讲
下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②③④
2
A
典题精讲
如图,△A′B′C ′是△ABC 以点O 为位似中心经过位似变换得到的,若△A′B′C ′的面积与△ABC 的面积比是4∶9,则OB ′∶OB 为( )
A.2∶3
B.3∶2
C.4∶5
D.4∶9
3
A
探索新知
3
知识点
位似图形的画法
探究:
如果在四边形ABCD 外任取一点O,分别在OA,QB,OC,OD 的反向延长线上取点A′ ,B ′ ,C ′ ,D ′ ,使得
四边形A′B ′C ′D ′ 与四边形ABCD 有什么关系?如果点O 取在四边形ABCD 内部呢?
分别画出得到的四边形A′B ′C ′D ′ .
探索新知
例如,要把四边形ABCD 缩小到原来的
以在四边形ABCD 外任取一点O(如图),分别在线段
OA,OB,OC,OD上取点A′ ,B ′ ,C ′ ,D ′ ,使得
顺次连接点A′ ,B ′ ,C ′ ,
D ′, 所得四边形A′B ′C ′D ′就是所要求的图形 .
我们可
探索新知
画位似多边形的一般步骤:
(1)确定位似中心;
(2)分别连接位似中心和能代
表原多边形的关键点;
(3)根据位似比,利用截取的方法,找出所作的位似
多边形的对应点;
(4)顺次连接上述各点,得到放大或缩小的多边形.
探索新知
例3 如图,在6×8网格图中,每个小正方形边长均为1,点O 和
△ABC 的顶点均为小正方形的顶点.
(1)以O 为位似中心,在网格图中作△A′B ′C ′,使△A′B ′C ′和
△ABC 位似,且位似比为 1∶2;
(2) 连接(1)中的AA′,求四边形AA′C ′C 的周长.(结果保留根号)
探索新知
分析:(1)根据位似比是1∶2,画出以O 为位似中心的△A′B ′C ′;
(2)根据勾股定理求出AC,A′C ′的长,由于AA′,CC ′的
长易得,相加即可求得四边形AA′C ′C 的周长.
解:(1)如图所示:
(2)AA′=CC ′=2.
在Rt△OA′C ′中,
OA′=OC ′=2,得A′C ′=
同理可得AC=
∴四边形AA′C′C的周长=
典题精讲
如图,以点O 为位似中心,将△ ABC 放大为原来的3倍.
解:如图所示的△A′B′C ′或△A″B″C ″就是所要求作的三角形.
.
O
C
A
B
典题精讲
如图是△ABC 位似图形的几种画法,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
易错提醒
如图,正方形网格中有一条简笔画“鱼”,请你以点D 为位似中心将其放大,使新图形与原图形的对应线段的比是2∶1,画出符合条件的所有图形.(不要求写作法)
易错提醒
易错点:对位似变换时图形的位置考虑不全而漏解.
解:
如图:
易错总结:此题易忽略其中一种情况,当题中对位似图形
的位置没有限制条件时,一定要考虑全面.
学以致用
小试牛刀
如图,点O 是五边形ABCDE 和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则C1D1:CD=( )
A.1:2
B.1:3
C.3:1
D.1:4
1
C
小试牛刀
如图,△ABC 与△DEF 是位似图形,点O 是位似中心,相似比是1:2,已知DE=4,则AB 的长是( )
A.2
B.4
C.8
D.1
2
A
小试牛刀
如图,在10×10的正方形网格中,点A,B,C,D 均在格点上,以点A 为位似中心画四边形AB′C′D′,使它与四边形ABCD 位似,且相似比为2.
(1)在图中画出四边形AB′C′D ′;
(2)填空:△AC′D ′是__________
三角形.
3
等腰直角
小试牛刀
4 如图, ABCD 的对角线AC,BD 相交于点O,点E,F,
G,H 分别是线段OA,OB,OC,OD 的中点,那么
ABCD 与四边形EFGH 是否是位似图形?为什么?
小试牛刀
解:
是.
理由:∵点E,F 分别是OA,OB 的中点,∴FE= AB,FE∥AB.
∵点G,H 分别是OC,OD 的中点,∴HG= CD,HG∥CD.
∵四边形ABCD 是平行四边形,∴AB=CD,AB∥CD. ∴EF=HG,FE∥HG. ∴四边形EFGH 是平行四边形.
∵FE∥AB,∴∠OEF=∠OAB.
同理∠OEH=∠OAD,∴∠HEF=∠DAB,
同理∠EFG=∠ABC,∠FGH=∠BCD,∠GHE=∠CDA.
又易得 ,∴ EFGH∽ ABCD.
又 ∵它们的对应顶点的连线相交于点O,
∴ ABCD 与四边形EFGH 是位似图形,O为位似中心.
小试牛刀
如图,△ABC 与△A′B ′C ′是位似图形,点A,B,A′,B ′,
O 共线,点O 为位似中心.
(1)AC 与A′C ′平行吗?为什么?
(2)若AB=2A′B ′,OC ′=5,求CC ′的长.
小试牛刀
(1)AC∥A′C ′.理由如下:∵△ABC 与△A′B ′C ′是位似图形,
∴△ABC∽△A′B ′C ′. ∴∠A=∠C ′A′B ′. ∴AC∥A′C ′.
(2)由(1)知△ABC∽△A′B ′C ′,
∴ . ∵AB=2A′B ′,∴ .
又∵△ABC 与△A′B ′C ′是位似图形,
∴
∵OC ′=5,∴OC=10.
∴CC ′=OC-OC ′=10-5=5.
解:
小试牛刀
如图,已知△DEO 与△ABO 是位似图形,△OEF 与△OBC
是位似图形.
求证:OD ·OC=OF ·OA.
证明:
∵△DEO 与△ABO 是位似图形,
∴
又∵△OEF 与△OBC 是位似图形,
∴
∴ ,即OD ·OC=OF ·OA.
小试牛刀
如图,在6×8的网格图中,每个小正方形的边长均为1,
点O 和△ABC 的顶点均在小正方形的顶点上.
(1)以O 为位似中心,在网格图中作△A′B ′C ′和△ABC
位似,且相似比为1∶2;
(2)连接(1)中的AA′,求四边形AA′C ′C 的周长(结果保
留根号).
小试牛刀
(1)如图.
(2)如图,四边形AA′C ′C 的周长为AA′+A′C ′+CC ′+AC=2+2 +2+4 =4+6 .
解:
小试牛刀
8 如图,在矩形ABCD 中,对角线AC,BD 相交于点O.
(1)过点O 作OE⊥BC 于点E,连接DE 交OC 于点F,作
FG⊥BC 于点G,则△ABC 和△FGC 是位似图形吗?
若是,请写出位似中心,并求出相似比;若不是,
请说明理由.
(2)连接DG 交OC 于点H,作HI⊥BC 于点I,试确定CI∶BC
的值(直接写出结果).
小试牛刀
(1)△ABC 与△FGC 是位似图形,位似中心是点C,
在矩形ABCD 中,AD∥BC,∴△AFD∽△CFE.
∴ . 又∵AD=BC,∴ .
∵∠ABC=90°,OE⊥BC,∴OE∥AB.
又∵OA=OC,∴CE=BC,
∴ . ∴ ,
即△ABC 与△FGC 的相似比为3∶1.
(2)CI∶BC=1∶4.
解:
小试牛刀
如图,某小区原有一矩形花坛,现对小区进行规划,按要求作出相应的位似图形.
(1)在原地将花坛扩建,使各边的对应边为原来的3倍;
(2)在异地修建一块矩形草坪,使它与花坛的对应边的比为4∶1,
你能设计出图纸吗?
小试牛刀
解:
(1)取矩形ABCD 的对角线的交点O 为位似中心,
①作射线OA,OB,OC,OD;
②分别在射线OA,OB,OC,OD上取点E,F,G,
H,使得 =3;
③连接EF,FG,GH,HE,四边形EFGH 即为所求
作的图形,如图所示.
小试牛刀
(2)能.在矩形ABCD 外取一点O 为位似中心,
①作射线OA,OB,OC,OD;
②分别在射线OA,OB,OC,OD上取E ′,F ′,G ′,
H ′,使得 =4;
③连接E ′F ′,F ′G ′,G ′H ′,H ′E ′,四边形E ′F ′G ′H ′即
为所求作的矩形草坪图,如图所示.
课堂小结
课堂小结
1. 位似图形的概念
2.位似图形的性质
位似图形的对应点和位似中心在同一条直线上,它们到位
似中心的距离之比等于相似比. (位似比)
如果两个相似图形的每组对应点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心 .
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.3 位似
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
在幻灯机放映图片的过程中,这些图片有什么关系呢?
幻灯机在哪儿呢?
放幻灯片
A’
B’
D’
C’
A
B
D
C
新课精讲
探索新知
1
知识点
位似图形的认识
这两个图形有哪些特征呢?
1.两图形相似;
2.每组对应点所在直线都经过同一点;
3. 对应边互相平行.
探索新知
如果两个相似图形的每组对应点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个交点叫做位似中心 .
如果两个
A
B
D
C
A’
B’
D’
C’
O
探索新知
1.两图形相似;
同时满足下面三个条件的两个图形才叫做位似图形.三条件缺一不可.
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
2.每组对应点所在直线都经过同一点;
3. 对应边互相平行.
探索新知
例1 判断如图所示的各图中的两个图形是否是位似图形,
如果是,请指出其位似中心.
解:(1)是位似图形,位似中心为点A;
(2)是位似图形,位似中心为点P;
(3)不是位似图形;
(4)是位似图形,位似中心为点O;
(5)不是位似图形.
典题精讲
如图所示两个四边形是位似图形,它们的位似中心是( )
A.点M
B.点N
C.点O
D.点P
D
典题精讲
对于平面图形上的任意两点P,Q,如果经过某种变换得到新图形上的对应点P ′,Q ′,保持PQ=P′Q ′,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是( )
A.平移 B.旋转
C.轴对称 D.位似
2
D
典题精讲
利用位似图形将一个图形放大或缩小时,首先要选取一点作为位似中心,那么位似中心可以在( )
A.图形外 B.图形内
C.图形上 D.以上都可以
3
D
探索新知
2
知识点
位似图形的性质
图中有多边形相似吗?如果有,那么这种相似有什么特征?
C
B
B’
C’
O
A’
A
A
B
D
C
E
F
P
探索新知
位似图形上任意一对对应点到位似中心的距离之比等于位似比.
1. 位似图形的对应点和位似中心在同一条直线上;
位似图形有以下性质:
探索新知
例2 △ABC 与△A′B ′C ′是位似图形,且△ABC 与△A′B ′C ′的位似比
是1∶2,已知△ABC 的面积是3,则△A′B ′C ′的面积是( )
A. 3 B. 6 C. 9 D. 12
导引:∵△ABC 与△A′B ′C ′是位似图形,且△ABC 与
△A′B ′C ′的位似比是1∶2,
∴△ABC 与△A′B ′C ′相似,且相似比为1∶2.
∴△ABC 与△A′B ′C ′的面积比为1∶4.
∵△ABC 的面积是3,∴△A′B ′C ′的面积是12.
D
探索新知
总 结
两个图形位似,则两个图形相似,所以相似图形的性质,位似图形都满足,可以直接运用.
典题精讲
如图,△OAB 和△OCD 是位似图形,AB 与CD 平行吗?为什么?
解:AB∥CD. 理由如下:
∵△OAB 和△OCD 是位似图形,
∴△OAB∽△OCD.
∴∠OAB=∠C.
∴AB∥CD.
A
B
O
D
C
典题精讲
下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②③④
2
A
典题精讲
如图,△A′B′C ′是△ABC 以点O 为位似中心经过位似变换得到的,若△A′B′C ′的面积与△ABC 的面积比是4∶9,则OB ′∶OB 为( )
A.2∶3
B.3∶2
C.4∶5
D.4∶9
3
A
探索新知
3
知识点
位似图形的画法
探究:
如果在四边形ABCD 外任取一点O,分别在OA,QB,OC,OD 的反向延长线上取点A′ ,B ′ ,C ′ ,D ′ ,使得
四边形A′B ′C ′D ′ 与四边形ABCD 有什么关系?如果点O 取在四边形ABCD 内部呢?
分别画出得到的四边形A′B ′C ′D ′ .
探索新知
例如,要把四边形ABCD 缩小到原来的
以在四边形ABCD 外任取一点O(如图),分别在线段
OA,OB,OC,OD上取点A′ ,B ′ ,C ′ ,D ′ ,使得
顺次连接点A′ ,B ′ ,C ′ ,
D ′, 所得四边形A′B ′C ′D ′就是所要求的图形 .
我们可
探索新知
画位似多边形的一般步骤:
(1)确定位似中心;
(2)分别连接位似中心和能代
表原多边形的关键点;
(3)根据位似比,利用截取的方法,找出所作的位似
多边形的对应点;
(4)顺次连接上述各点,得到放大或缩小的多边形.
探索新知
例3 如图,在6×8网格图中,每个小正方形边长均为1,点O 和
△ABC 的顶点均为小正方形的顶点.
(1)以O 为位似中心,在网格图中作△A′B ′C ′,使△A′B ′C ′和
△ABC 位似,且位似比为 1∶2;
(2) 连接(1)中的AA′,求四边形AA′C ′C 的周长.(结果保留根号)
探索新知
分析:(1)根据位似比是1∶2,画出以O 为位似中心的△A′B ′C ′;
(2)根据勾股定理求出AC,A′C ′的长,由于AA′,CC ′的
长易得,相加即可求得四边形AA′C ′C 的周长.
解:(1)如图所示:
(2)AA′=CC ′=2.
在Rt△OA′C ′中,
OA′=OC ′=2,得A′C ′=
同理可得AC=
∴四边形AA′C′C的周长=
典题精讲
如图,以点O 为位似中心,将△ ABC 放大为原来的3倍.
解:如图所示的△A′B′C ′或△A″B″C ″就是所要求作的三角形.
.
O
C
A
B
典题精讲
如图是△ABC 位似图形的几种画法,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
易错提醒
如图,正方形网格中有一条简笔画“鱼”,请你以点D 为位似中心将其放大,使新图形与原图形的对应线段的比是2∶1,画出符合条件的所有图形.(不要求写作法)
易错提醒
易错点:对位似变换时图形的位置考虑不全而漏解.
解:
如图:
易错总结:此题易忽略其中一种情况,当题中对位似图形
的位置没有限制条件时,一定要考虑全面.
学以致用
小试牛刀
如图,点O 是五边形ABCDE 和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则C1D1:CD=( )
A.1:2
B.1:3
C.3:1
D.1:4
1
C
小试牛刀
如图,△ABC 与△DEF 是位似图形,点O 是位似中心,相似比是1:2,已知DE=4,则AB 的长是( )
A.2
B.4
C.8
D.1
2
A
小试牛刀
如图,在10×10的正方形网格中,点A,B,C,D 均在格点上,以点A 为位似中心画四边形AB′C′D′,使它与四边形ABCD 位似,且相似比为2.
(1)在图中画出四边形AB′C′D ′;
(2)填空:△AC′D ′是__________
三角形.
3
等腰直角
小试牛刀
4 如图, ABCD 的对角线AC,BD 相交于点O,点E,F,
G,H 分别是线段OA,OB,OC,OD 的中点,那么
ABCD 与四边形EFGH 是否是位似图形?为什么?
小试牛刀
解:
是.
理由:∵点E,F 分别是OA,OB 的中点,∴FE= AB,FE∥AB.
∵点G,H 分别是OC,OD 的中点,∴HG= CD,HG∥CD.
∵四边形ABCD 是平行四边形,∴AB=CD,AB∥CD. ∴EF=HG,FE∥HG. ∴四边形EFGH 是平行四边形.
∵FE∥AB,∴∠OEF=∠OAB.
同理∠OEH=∠OAD,∴∠HEF=∠DAB,
同理∠EFG=∠ABC,∠FGH=∠BCD,∠GHE=∠CDA.
又易得 ,∴ EFGH∽ ABCD.
又 ∵它们的对应顶点的连线相交于点O,
∴ ABCD 与四边形EFGH 是位似图形,O为位似中心.
小试牛刀
如图,△ABC 与△A′B ′C ′是位似图形,点A,B,A′,B ′,
O 共线,点O 为位似中心.
(1)AC 与A′C ′平行吗?为什么?
(2)若AB=2A′B ′,OC ′=5,求CC ′的长.
小试牛刀
(1)AC∥A′C ′.理由如下:∵△ABC 与△A′B ′C ′是位似图形,
∴△ABC∽△A′B ′C ′. ∴∠A=∠C ′A′B ′. ∴AC∥A′C ′.
(2)由(1)知△ABC∽△A′B ′C ′,
∴ . ∵AB=2A′B ′,∴ .
又∵△ABC 与△A′B ′C ′是位似图形,
∴
∵OC ′=5,∴OC=10.
∴CC ′=OC-OC ′=10-5=5.
解:
小试牛刀
如图,已知△DEO 与△ABO 是位似图形,△OEF 与△OBC
是位似图形.
求证:OD ·OC=OF ·OA.
证明:
∵△DEO 与△ABO 是位似图形,
∴
又∵△OEF 与△OBC 是位似图形,
∴
∴ ,即OD ·OC=OF ·OA.
小试牛刀
如图,在6×8的网格图中,每个小正方形的边长均为1,
点O 和△ABC 的顶点均在小正方形的顶点上.
(1)以O 为位似中心,在网格图中作△A′B ′C ′和△ABC
位似,且相似比为1∶2;
(2)连接(1)中的AA′,求四边形AA′C ′C 的周长(结果保
留根号).
小试牛刀
(1)如图.
(2)如图,四边形AA′C ′C 的周长为AA′+A′C ′+CC ′+AC=2+2 +2+4 =4+6 .
解:
小试牛刀
8 如图,在矩形ABCD 中,对角线AC,BD 相交于点O.
(1)过点O 作OE⊥BC 于点E,连接DE 交OC 于点F,作
FG⊥BC 于点G,则△ABC 和△FGC 是位似图形吗?
若是,请写出位似中心,并求出相似比;若不是,
请说明理由.
(2)连接DG 交OC 于点H,作HI⊥BC 于点I,试确定CI∶BC
的值(直接写出结果).
小试牛刀
(1)△ABC 与△FGC 是位似图形,位似中心是点C,
在矩形ABCD 中,AD∥BC,∴△AFD∽△CFE.
∴ . 又∵AD=BC,∴ .
∵∠ABC=90°,OE⊥BC,∴OE∥AB.
又∵OA=OC,∴CE=BC,
∴ . ∴ ,
即△ABC 与△FGC 的相似比为3∶1.
(2)CI∶BC=1∶4.
解:
小试牛刀
如图,某小区原有一矩形花坛,现对小区进行规划,按要求作出相应的位似图形.
(1)在原地将花坛扩建,使各边的对应边为原来的3倍;
(2)在异地修建一块矩形草坪,使它与花坛的对应边的比为4∶1,
你能设计出图纸吗?
小试牛刀
解:
(1)取矩形ABCD 的对角线的交点O 为位似中心,
①作射线OA,OB,OC,OD;
②分别在射线OA,OB,OC,OD上取点E,F,G,
H,使得 =3;
③连接EF,FG,GH,HE,四边形EFGH 即为所求
作的图形,如图所示.
小试牛刀
(2)能.在矩形ABCD 外取一点O 为位似中心,
①作射线OA,OB,OC,OD;
②分别在射线OA,OB,OC,OD上取E ′,F ′,G ′,
H ′,使得 =4;
③连接E ′F ′,F ′G ′,G ′H ′,H ′E ′,四边形E ′F ′G ′H ′即
为所求作的矩形草坪图,如图所示.
课堂小结
课堂小结
1. 位似图形的概念
2.位似图形的性质
位似图形的对应点和位似中心在同一条直线上,它们到位
似中心的距离之比等于相似比. (位似比)
如果两个相似图形的每组对应点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心 .
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
