【班海精品】人教版(新)九下-28.1 锐角三角函数 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-28.1 锐角三角函数 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览





文档简介
(共38张PPT)
28.1 锐角三角函数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
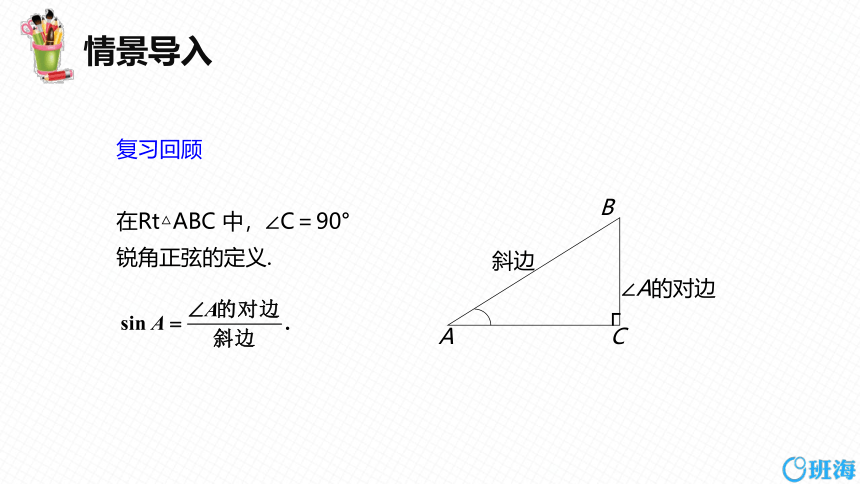
复习回顾
在Rt△ABC 中,∠C=90°
锐角正弦的定义.
A
B
C
∠A的对边
┌
斜边
新课精讲
探索新知
1
知识点
余弦函数
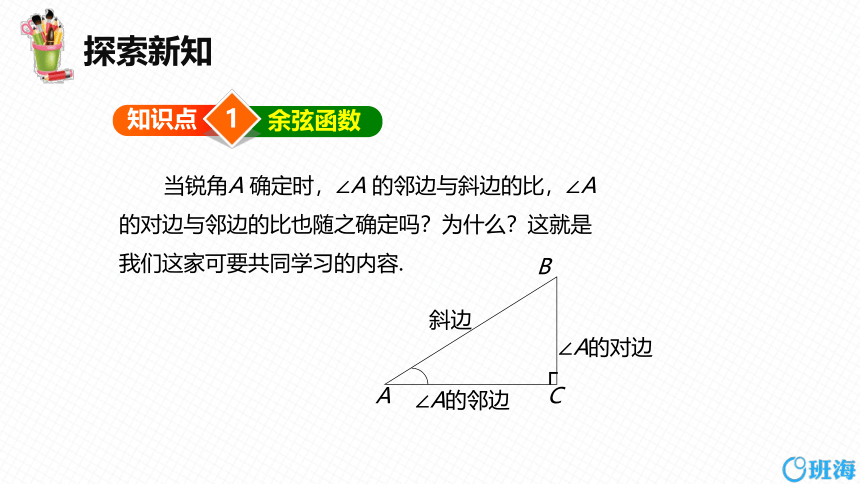
当锐角A 确定时,∠A 的邻边与斜边的比,∠A
的对边与邻边的比也随之确定吗?为什么?这就是
我们这家可要共同学习的内容.
A
B
C
∠A的对边
┌
斜边
∠A的邻边
探索新知
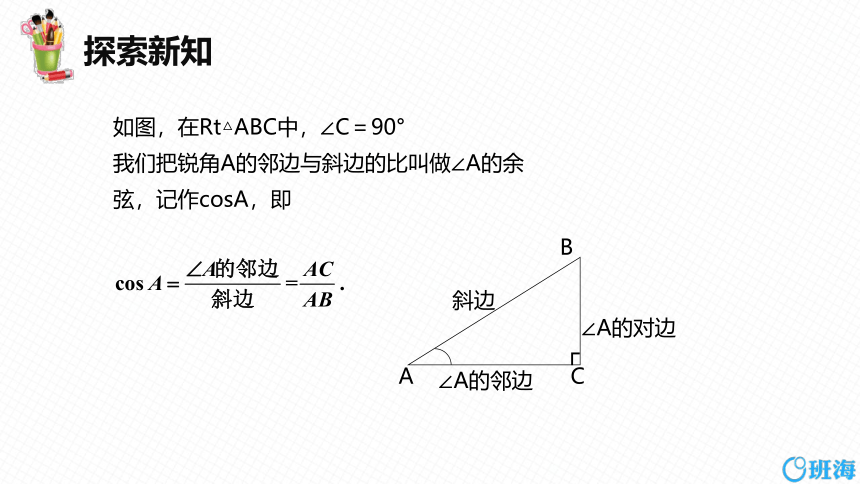
如图,在Rt△ABC中,∠C=90°
我们把锐角A的邻边与斜边的比叫做∠A的余
弦,记作cosA,即
A
B
C
∠A的对边
┌
斜边
∠A的邻边
探索新知
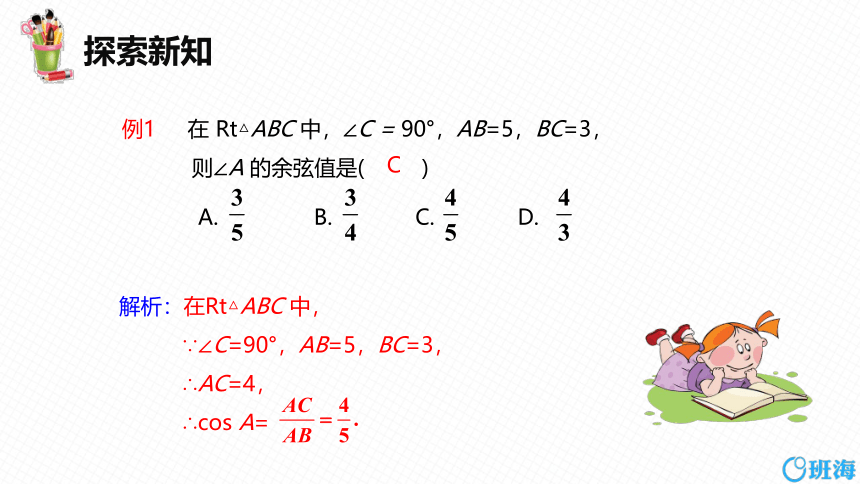
例1 在 Rt△ABC 中,∠C = 90°,AB=5,BC=3,
则∠A 的余弦值是( )
A. B. C. D.
解析:在Rt△ABC 中,
∵∠C=90°,AB=5,BC=3,
∴AC=4,
∴cos A=
C
探索新知
总 结
特别提醒求出所需要的边的值,紧扣余弦概念,一定要认清是角的邻边与斜边的比,否则会和正弦混淆.
典题精讲
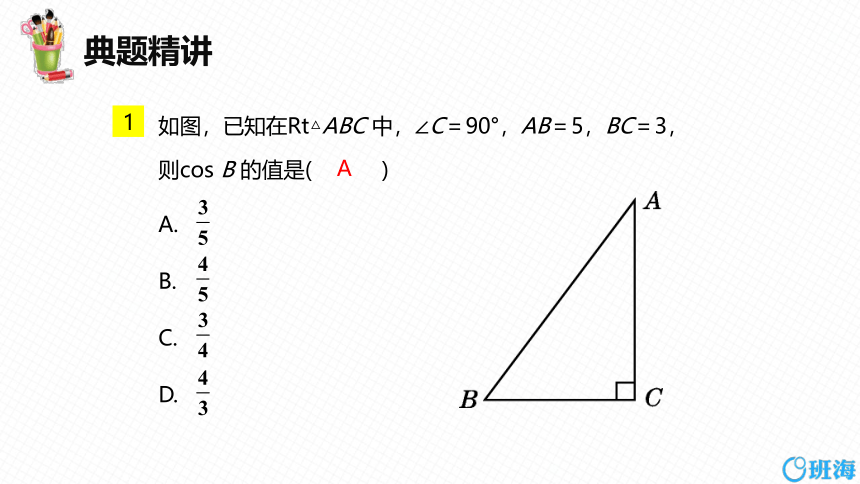
如图,已知在Rt△ABC 中,∠C=90°,AB=5,BC=3,
则cos B 的值是( )
A.
B.
C.
D.
1
A
典题精讲
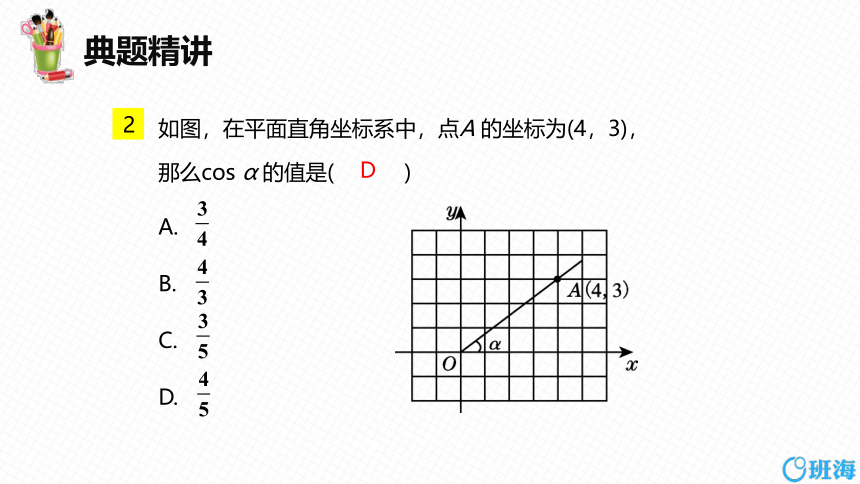
如图,在平面直角坐标系中,点A 的坐标为(4,3),
那么cos α 的值是( )
A.
B.
C.
D.
2
D
探索新知
2
知识点
正切函数
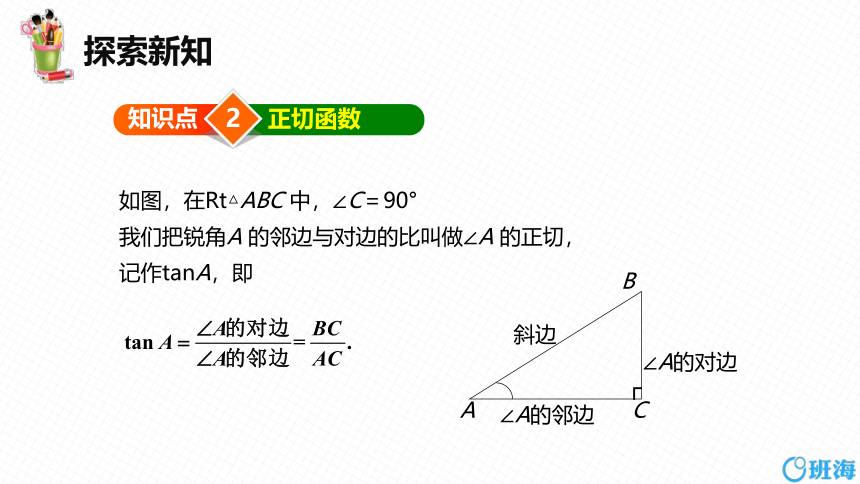
如图,在Rt△ABC 中,∠C=90°
我们把锐角A 的邻边与对边的比叫做∠A 的正切,
记作tanA,即
A
B
C
∠A的对边
┌
斜边
∠A的邻边
探索新知
例2 如图,在 Rt△ABC 中,∠C = 90°,
AB=10,BC=6,求sin A,cos A,
tan A的值.
解: 由勾股定理得
因此
A
B
C
6
┌
10
探索新知
总 结
已知直角三角形的任意两边长求某个锐角的三角函数值时,运用数形结合思想,首先画出符合题意的直角三角形,然后根据勾股定理求出未知边长,最后结合锐角三角函数的定义求三角函数值.
典题精讲
分别求出下列直角三角形中两个
锐角的正弦值、余弦值和正切值.
解: 由勾股定理得
因此
A
B
C
┌
13
(1)
典题精讲
解:
所以
B
A
C
┌
3
2
(2)
典题精讲
在Rt△ABC 中,∠C=90°,AB=5,BC=3,则tan A
的值是( )
A. B. C. D.
2
A
在Rt△ABC 中,∠C=90°,若斜边AB 是直角边BC 的3倍,
则tan B 的值是( )
A. B. 3
C. D.
3
D
典题精讲
如图,在△ABC 中,∠BAC=90°,AB=AC,点D 为边AC 的中点,DE⊥BC 于点E,连接BD,则tan ∠DBC 的值为( )
A.
B.
C.
D.
4
A
典题精讲
△ABC 在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC 于D,下列选项中,错误的是( )
A.sin α=cos α
B.tan C=2
C.sin β=cos β
D.tan α=1
5
C
典题精讲
如图,点A,B,O 是正方形网格上的三个格点,⊙O 的半径为OA,点P 是AmB上的一点,则tan∠APB 的值是( )
A. 1
B.
C.
D.
6
︵
A
易错提醒
已知x=cos α (α为锐角)满足方程2x 2-5x+2=0,
求cos α 的值.
解:
∵方程2x 2-5x+2=0的解是x1=2,x2= ,
又∵0<cos α<1(α为锐角), ∴cos α= .
易错提醒
易错点:忽视锐角三角函数值的范围而致错.
常见错解:∵方程2x 2-5x+2=0的解是x1=2,x2= ,
∴cos α=2或cos α= .忽略了cos α (α 为锐角)
的取值范围是0<cos α<1.
学以致用
小试牛刀
如图,已知AB 是半圆O 的直径,弦AD,BC 相交于点P,如果∠DPB=α,那么 等于( )
A.sin α
B.cos α
C.tan α
D.
1
B
小试牛刀
如果方程x 2-4x+3=0的两个根分别是Rt△ABC 的两条边长,△ABC 最小的角为∠A,那么tan A的值为______________.
2
小试牛刀
如图,在Rt△ABC 中,∠B=90°,∠A=30°,以点A 为圆心,
BC 长为半径画弧交AB 于点D,分别以点A,D 为圆心,AB
长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD 的余
弦值是( )
A.
B.
C.
D.
3
B
小试牛刀
如图,在 ABCD 中,对角线AC 与BD 相交于点O,∠CAB=∠ACB,
过点B 作BE⊥AB 交AC 于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB= ,
求线段OE 的长.
小试牛刀
(1)证明:∵∠CAB=∠ACB,∴AB=CB.
∴ ABCD是菱形.∴AC⊥BD.
(2)解:在Rt△AOB 中,cos ∠OAB= ,AB=14,
∴AO= AB= .
在Rt△ABE 中,cos ∠EAB= ,
AB=14,∴AE= AB=16,
∴OE=AE-AO=16- .
小试牛刀
如图,在等腰三角形ABC 中,AC=BC=10,AB=12,
以BC 为直径作⊙O 交AB 于点D,交AC 于点G,DF⊥AC,
垂足为F,交CB 的延长线于点E.
(1)求证:直线EF 是⊙O 的切线;
(2)求cos E 的值.
小试牛刀
(1)证明:如图,连接OD,CD.∵BC 是直径,
∴CD⊥AB. ∵AC=BC,∴D 是AB
的中点.又∵O 为CB 的中点,∴OD∥AC.
∵DF⊥AC,∴OD⊥EF,∴EF 是⊙O 的切线.
(2)解:如图,连接BG. ∵BC 是直径,∴∠BGC=90°.
在Rt△ACD 中,DC= =8.
∵AB ·CD=2S△ABC=AC ·BG,
∴BG=
∵BG⊥AC,DF⊥AC,∴BG∥EF,∴∠E=∠CBG.
∴cos E=cos ∠CBG=
小试牛刀
如图,已知四边形ABCD 内接于⊙O,A是 的中点,
AE⊥AC 于A,与⊙O 及CB 的延长线交于点F,E,且 .
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD 的值.
小试牛刀
(1)证明:∵四边形ABCD 内接于⊙O,∴∠CDA=∠ABE,
∵ ,∴∠DCA=∠BAE,
∴△ADC∽△EBA.
(2)解:∵A是 的中点,∴ ,∴AB=AC=8.
∵△ADC∽△EBA,∴∠CAD=∠E, ,
∴ ,∴AE= ,
∴tan∠CAD =tan∠E =
小试牛刀
如图,抛物线 y=-x 2+3x+4与x 轴交于A,B 两点,
与y 轴交于C 点,点D 在抛物线上且横坐标为3.
(1)求tan∠DBC 的值;
(2)点P 为抛物线上一点,且∠DBP=45°,求点P 的坐标.
小试牛刀
解:
(1)令x=0,则y=4. ∴C (0,4).令y=0,则-x 2+3x+4=0,
解得x1=-1,x2=4. ∴A (-1,0),B (4,0).当x=3时,
y=-32+3×3+4=4, ∴D (3,4).在Rt△OBC 中,OC=OB=4,
∴∠ABC=45°,BC=4 .如图,连接CD,过D 作DE⊥BC 于E.
∵C (0,4),∴CD∥AB,∴∠BCD=∠ABC=45°.在Rt△CDE 中,
CD=3,∴CE=DE= ,∴BE=BC-CE= ,
∴tan ∠DBC= .
小试牛刀
(2)如图,过P 作PF⊥x 轴于F.
∵∠CBF=∠DBP=45°,∴∠PBF=∠DBC,
∴tan ∠PBF= .
设P (x,-x 2+3x+4),则 ,
解得x1=- ,x2=4(舍去),
∴P .
课堂小结
课堂小结
(1)∠A 的邻边与斜边的比叫做∠A 的余弦,记作cos A,
即cos A=
(2)∠A 的对边与邻边的比叫做∠A 的正切,记作tan A,
即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A 的邻边b
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.1 锐角三角函数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
在Rt△ABC 中,∠C=90°
锐角正弦的定义.
A
B
C
∠A的对边
┌
斜边
新课精讲
探索新知
1
知识点
余弦函数
当锐角A 确定时,∠A 的邻边与斜边的比,∠A
的对边与邻边的比也随之确定吗?为什么?这就是
我们这家可要共同学习的内容.
A
B
C
∠A的对边
┌
斜边
∠A的邻边
探索新知
如图,在Rt△ABC中,∠C=90°
我们把锐角A的邻边与斜边的比叫做∠A的余
弦,记作cosA,即
A
B
C
∠A的对边
┌
斜边
∠A的邻边
探索新知
例1 在 Rt△ABC 中,∠C = 90°,AB=5,BC=3,
则∠A 的余弦值是( )
A. B. C. D.
解析:在Rt△ABC 中,
∵∠C=90°,AB=5,BC=3,
∴AC=4,
∴cos A=
C
探索新知
总 结
特别提醒求出所需要的边的值,紧扣余弦概念,一定要认清是角的邻边与斜边的比,否则会和正弦混淆.
典题精讲
如图,已知在Rt△ABC 中,∠C=90°,AB=5,BC=3,
则cos B 的值是( )
A.
B.
C.
D.
1
A
典题精讲
如图,在平面直角坐标系中,点A 的坐标为(4,3),
那么cos α 的值是( )
A.
B.
C.
D.
2
D
探索新知
2
知识点
正切函数
如图,在Rt△ABC 中,∠C=90°
我们把锐角A 的邻边与对边的比叫做∠A 的正切,
记作tanA,即
A
B
C
∠A的对边
┌
斜边
∠A的邻边
探索新知
例2 如图,在 Rt△ABC 中,∠C = 90°,
AB=10,BC=6,求sin A,cos A,
tan A的值.
解: 由勾股定理得
因此
A
B
C
6
┌
10
探索新知
总 结
已知直角三角形的任意两边长求某个锐角的三角函数值时,运用数形结合思想,首先画出符合题意的直角三角形,然后根据勾股定理求出未知边长,最后结合锐角三角函数的定义求三角函数值.
典题精讲
分别求出下列直角三角形中两个
锐角的正弦值、余弦值和正切值.
解: 由勾股定理得
因此
A
B
C
┌
13
(1)
典题精讲
解:
所以
B
A
C
┌
3
2
(2)
典题精讲
在Rt△ABC 中,∠C=90°,AB=5,BC=3,则tan A
的值是( )
A. B. C. D.
2
A
在Rt△ABC 中,∠C=90°,若斜边AB 是直角边BC 的3倍,
则tan B 的值是( )
A. B. 3
C. D.
3
D
典题精讲
如图,在△ABC 中,∠BAC=90°,AB=AC,点D 为边AC 的中点,DE⊥BC 于点E,连接BD,则tan ∠DBC 的值为( )
A.
B.
C.
D.
4
A
典题精讲
△ABC 在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC 于D,下列选项中,错误的是( )
A.sin α=cos α
B.tan C=2
C.sin β=cos β
D.tan α=1
5
C
典题精讲
如图,点A,B,O 是正方形网格上的三个格点,⊙O 的半径为OA,点P 是AmB上的一点,则tan∠APB 的值是( )
A. 1
B.
C.
D.
6
︵
A
易错提醒
已知x=cos α (α为锐角)满足方程2x 2-5x+2=0,
求cos α 的值.
解:
∵方程2x 2-5x+2=0的解是x1=2,x2= ,
又∵0<cos α<1(α为锐角), ∴cos α= .
易错提醒
易错点:忽视锐角三角函数值的范围而致错.
常见错解:∵方程2x 2-5x+2=0的解是x1=2,x2= ,
∴cos α=2或cos α= .忽略了cos α (α 为锐角)
的取值范围是0<cos α<1.
学以致用
小试牛刀
如图,已知AB 是半圆O 的直径,弦AD,BC 相交于点P,如果∠DPB=α,那么 等于( )
A.sin α
B.cos α
C.tan α
D.
1
B
小试牛刀
如果方程x 2-4x+3=0的两个根分别是Rt△ABC 的两条边长,△ABC 最小的角为∠A,那么tan A的值为______________.
2
小试牛刀
如图,在Rt△ABC 中,∠B=90°,∠A=30°,以点A 为圆心,
BC 长为半径画弧交AB 于点D,分别以点A,D 为圆心,AB
长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD 的余
弦值是( )
A.
B.
C.
D.
3
B
小试牛刀
如图,在 ABCD 中,对角线AC 与BD 相交于点O,∠CAB=∠ACB,
过点B 作BE⊥AB 交AC 于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB= ,
求线段OE 的长.
小试牛刀
(1)证明:∵∠CAB=∠ACB,∴AB=CB.
∴ ABCD是菱形.∴AC⊥BD.
(2)解:在Rt△AOB 中,cos ∠OAB= ,AB=14,
∴AO= AB= .
在Rt△ABE 中,cos ∠EAB= ,
AB=14,∴AE= AB=16,
∴OE=AE-AO=16- .
小试牛刀
如图,在等腰三角形ABC 中,AC=BC=10,AB=12,
以BC 为直径作⊙O 交AB 于点D,交AC 于点G,DF⊥AC,
垂足为F,交CB 的延长线于点E.
(1)求证:直线EF 是⊙O 的切线;
(2)求cos E 的值.
小试牛刀
(1)证明:如图,连接OD,CD.∵BC 是直径,
∴CD⊥AB. ∵AC=BC,∴D 是AB
的中点.又∵O 为CB 的中点,∴OD∥AC.
∵DF⊥AC,∴OD⊥EF,∴EF 是⊙O 的切线.
(2)解:如图,连接BG. ∵BC 是直径,∴∠BGC=90°.
在Rt△ACD 中,DC= =8.
∵AB ·CD=2S△ABC=AC ·BG,
∴BG=
∵BG⊥AC,DF⊥AC,∴BG∥EF,∴∠E=∠CBG.
∴cos E=cos ∠CBG=
小试牛刀
如图,已知四边形ABCD 内接于⊙O,A是 的中点,
AE⊥AC 于A,与⊙O 及CB 的延长线交于点F,E,且 .
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD 的值.
小试牛刀
(1)证明:∵四边形ABCD 内接于⊙O,∴∠CDA=∠ABE,
∵ ,∴∠DCA=∠BAE,
∴△ADC∽△EBA.
(2)解:∵A是 的中点,∴ ,∴AB=AC=8.
∵△ADC∽△EBA,∴∠CAD=∠E, ,
∴ ,∴AE= ,
∴tan∠CAD =tan∠E =
小试牛刀
如图,抛物线 y=-x 2+3x+4与x 轴交于A,B 两点,
与y 轴交于C 点,点D 在抛物线上且横坐标为3.
(1)求tan∠DBC 的值;
(2)点P 为抛物线上一点,且∠DBP=45°,求点P 的坐标.
小试牛刀
解:
(1)令x=0,则y=4. ∴C (0,4).令y=0,则-x 2+3x+4=0,
解得x1=-1,x2=4. ∴A (-1,0),B (4,0).当x=3时,
y=-32+3×3+4=4, ∴D (3,4).在Rt△OBC 中,OC=OB=4,
∴∠ABC=45°,BC=4 .如图,连接CD,过D 作DE⊥BC 于E.
∵C (0,4),∴CD∥AB,∴∠BCD=∠ABC=45°.在Rt△CDE 中,
CD=3,∴CE=DE= ,∴BE=BC-CE= ,
∴tan ∠DBC= .
小试牛刀
(2)如图,过P 作PF⊥x 轴于F.
∵∠CBF=∠DBP=45°,∴∠PBF=∠DBC,
∴tan ∠PBF= .
设P (x,-x 2+3x+4),则 ,
解得x1=- ,x2=4(舍去),
∴P .
课堂小结
课堂小结
(1)∠A 的邻边与斜边的比叫做∠A 的余弦,记作cos A,
即cos A=
(2)∠A 的对边与邻边的比叫做∠A 的正切,记作tan A,
即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A 的邻边b
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
