【班海精品】人教版(新)九下-28.1 锐角三角函数 第四课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-28.1 锐角三角函数 第四课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览










文档简介
(共44张PPT)
28.1 锐角三角函数
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
要测量教学楼的高度,小英身高1.6m.她在距离教学楼30m处测得仰角为25°,你能借助计算器估算出教学楼的高度吗 (精确到0.1m)
新课精讲
探索新知
1
知识点
用计算器求已知锐角的三角函数值
通过上面的学习,我们知道,当锐角A 是30°,45°或60°等特殊角时,可以求得这些特殊角的 锐角三角函数值;如果锐角A 不是这些特殊角, 怎样得到它的锐角三角函数值呢?
我们可以借助计算器求锐角三角函数值.
例如求sin18°,利用计算器的 键,并输入角度值18,
得到结果sin18°=0.309 016 994.
又如求tan30°36′,利用 键,并输入角的度、分值(可以使用 键),就可以得到结果0.591 398 351.
因为30°36′=30.6°,所以也可以利用 键,并输入角度值30.6,同样得到结果0.591 398 351.
探索新知
sin
tan
°′ ″
tan
探索新知
归 纳
利用计算器求锐角三角函数值:
1. 当锐角的大小以度为单位时,可先按 , ,
键,然后输入角度值(可以是整数,也可以是
小数),最后按 键,就可以在显示屏上显示出
结果;
2. 当锐角的大小以度、分、秒为单位时要借助
键计算,按键顺序是: (或 、 )、度数、
、分数、 、秒数、 、 .
sin
cos
tan
=
°′ ″
sin
cos
tan
°′ ″
°′ ″
°′ ″
=
探索新知
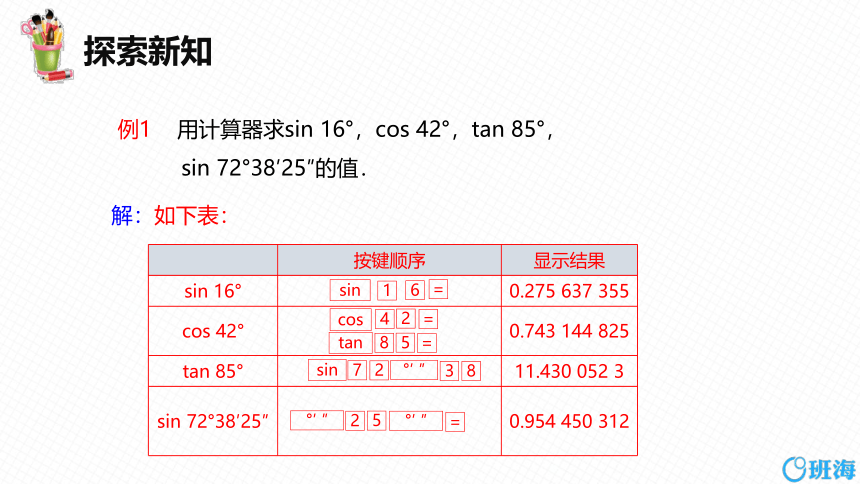
例1 用计算器求sin 16°,cos 42°,tan 85°,
sin 72°38′25″的值.
解:如下表:
按键顺序 显示结果
sin 16° 0.275 637 355
cos 42° 0.743 144 825
tan 85° 11.430 052 3
sin 72°38′25″ 0.954 450 312
sin
tan
sin
1
6
4
cos
2
8
5
2
5
2
7
3
8
=
=
=
=
°′ ″
°′ ″
°′ ″
探索新知
总 结
要注意不同型号的计算器的操作步骤可能有所不同.
典题精讲
1 用计算器求下列锐角三角函数值:
(1)sin 20°,cos 70°; sin 35°, cos 55°;
sin15°32′,cos74°28′;
(2)tan 3° 8',tan 80° 25′43".
(1)sin 20°≈0.342 0,cos 70°≈0.342 0;
sin 35°≈0.573 6,cos 55°≈0.573 6;
sin 15°32′≈0.267 8,cos 74°28′≈0.267 8.
(2)tan 3°8′≈0.054 7,tan 80°25′43″≈5.930 4.
解:
典题精讲
如图,是我们数学课上采用的科学计算器面板,利用该型号计算器计算 cos 55°,按键顺序正确的是( )
A.
B.
C.
D.
利用计算器求sin 30°时,依次按键
,则计算器上显示的结果是( )
A.0.5 B.0.707 C.0.866 D.1
sin
3
0
°′ ″
=
cos
2
5
5
×
=
cos
2
5
5
0
=
cos
2
5
5
=
cos
2
5
5
=
C
A
探索新知
2
知识点
用计算器求已知三角函数值的对应角
如果已知锐角三角函数值,也可以使用计算器求出相应锐角的度数.
例如,已知sin A=0. 501 8,用计算器求锐角A 可以按照下面方法操作:
依次按键 ,然后输入函数值0.501 8,得到∠A=30.119 158 67° (这说明锐角A精确到1°的结果为30°).
sin
2nd F
探索新知
还可以利用 键,进一步得到∠A=
30 °07′08.97″(这说明锐角A 精确到1′的结果为30°7′,精确到 1"的结果为30°7′9″).
2nd F
°′ ″
探索新知
归 纳
已知锐角三角函数值求锐角的度数:
如果是特殊角(30°, 45°,60°)的三角函数值,可直接写出其相应的角的度数;若不是特殊角的三角函数值,应利用计算器求角的度数.求角的度数要先按 键,将 、 、 转化成它们的第二功能键;当三角函数值为分数时,应先化成小数.
2nd F
sin
cos
tan
探索新知
例2 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sin A=0.516 8(结果精确到0.01°);
(2)cos A=0.675 3(结果精确到1″);
(3)tan A=0.189(结果精确到1°).
导引:已知锐角三角函数值,利用计算器求锐
角的度数时要注意先按 键.
2nd F
探索新知
解:(1)依次按键:
显示结果为:31.117 845 56,∠A≈31.12°.
(2)依次按键:
显示结果为:47°31′21.18″,
即 ∠A≈47°31′21″.
(3)依次按键:
显示结果为:10.702 657 49,即∠A≈11°.
sin
2nd F
0
5
1
6
8
=
,
2nd F
tan
0
9
1
8
=
,
2nd F
°′ ″
cos
0
3
7
6
5
=
2nd F
,
探索新知
总 结
计算器直接计算出的角的单位是度,而不是度、分、秒,因此若要得到用度、分、秒表示的角度,可以借助 和 键.
2nd F
°′ ″
典题精讲
已知下列锐角三角函数值,用计算器求其相应锐角的度数:
(1)sin A= 0. 627 5,sin B= 0.054 7;
(2)cos A= 0. 625 2,cos B= 0. 165 9;
(3)tan A= 4. 842 5,tan B= 0.881 6.
(1)∠A≈38°51′57″,∠B≈3°8′8″;
(2)∠A≈51°18′11″,∠B≈80°27′2″;
(3)∠A≈78°19′56″,∠B≈41°23′58″.
解:
典题精讲
已知α 为锐角,且tan α=3.387,下列各值中与α 最接近的是( )
A.73°33′ B.73°27′
C.16°27′ D.16°21′
在△ABC 中,∠C=90°,BC=5,AB=13,用科学计算器求∠A 约等于( )
A.24°38′ B.65°22′
C.67°23′ D.22°37′
2
3
A
D
探索新知
3
知识点
用计算器探究三角函数的性质
用计算器求下列各组锐角的三角函数值,从中你能
得出什么猜想?
(1)sin83°,cos7°;
(2)sin56°,cos34°;
(3) sin27°36′ , cos62°24′.
探索新知
2.用计算器求下列各组锐角的三角函数值,从中你能
得出什么猜想?
(1)sin13°, sin25°,sin36°,sin44° , sin57°,
sin68°, sin79°17′,sin83°27′53″;
(2)cos17°34′,cos34°27′53″,cos53°18′ ,
cos69°57′ 3″,cos77°17′ ,cos88°17′25″;
(3)tan27°34′,tan43°57′28″,tan52°18′15″ ,
tan67°,tan78°17′,tan85°24′ .
探索新知
1. 猜想:sin = cos(90°- ).
2. (1)猜想:对于锐角A,它的正弦函数 (sinA)的函数值随
自变量锐角A 的增大而增大,且sinA必满足 0 < sinA<1.
(2)猜想:对于锐角A,它的余弦函数(cosA)的函数值随锐角
A 的增大而减小,且cosA 必满足0 < cosA < 1.
(3)猜想:对于锐角A,它的正切函数(tanA)的函数值随锐角
A 的增大而增大 , 且tanA 满足0 < tanA.
探索新知
归 纳
(1)sin = cos(90°- ).
(2)对于锐角A,它的正弦函数 (sinA)的函数值随自变
量锐角A 的增大而增大,且sinA必满足0 < sinA<1.
(3)对于锐角A,它的余弦函数(cosA)的函数值随锐
角A 的增大而减小,且cosA 必满足0 < cosA < 1.
(4)对于锐角A,它的正切函数(tanA)的函数值随锐
角A 的增大而增大 , 且tanA 满足0 < tanA.
探索新知
例3 已知α+β=90°. 探究:
(1)sin α 与cos β 的关系;
(2)tan α 与tan β 的关系.
导引:根据α 和β 互余,可以将α 和β 放入同一个直角三角
形中,利用锐角三角函数的定义去探究互为余角的两
角的三角函数关系.
探索新知
解:如图,在Rt△ABC 中,∠C=90°,∠A=α,
∠B=β.
令∠A,∠B,∠C 所对的边分别是a,b,c.
(1)∵sin α= , cos β= ,
∴sin α=cos β.
(2)∵tan α= , tan β= ,
∴tan α · tan β=1.
探索新知
总 结
互为余角的两角的三角函数间的关系:
(1)任意锐角的正弦值等于它的余角的余弦值,即
sin α=cos (90°-α )或cos α=sin (90°-α );
(2)任意锐角的正切值与它的余角的正切值互为倒
数,即tan α · tan (90°-α )=1.
典题精讲
1 在Rt△ABC 中,∠C=90°,下列各式中正确的是( )
A.sin A=sin B B.tan A=tan B
C.sin A=cos B D.cos A=cos B
C
用计算器比较tan 25°,sin 27°,cos 26°的大小关系是( )
A.tan 25°B.tan 25°C.sin 27°D.cos 26°2
C
典题精讲
用计算器求sin 15°,sin 25°,sin 35°,sin 45°,sin 55°,sin 65°,sin 75°,sin 85°的值,研究sin α的值随锐角α变化的规律,根据这个规律判断:若A.30°<α<60° B.30°<α<90°
C.0°<α<60° D.60°<α<90°
3
A
易错提醒
用计算器求sin 35°29′的值(结果精确到0.001).
解:
sin 35°29′≈0.580.
易错点:不区分35°29′与35.29°而导致错误.
学以致用
小试牛刀
用计算器计算cos 44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
用计算器验证,下列等式正确的是( )
A.sin 18°24′+sin 35°36′=sin 54°
B.sin 65°54′-sin 35°54′=sin 30°
C.2sin 15°30′=sin 31°
D.sin 72°18′-sin 12°18′=sin 47°42′
1
B
2
D
小试牛刀
为了方便行人推车过某天桥,市政府在10 m高的天桥一侧修建了40 m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A. 2ndF sin 0 · 2 5 =
B. sin 2ndF 0 · 2 5 =
C. sin 0 · 2 5 =
D. 2ndF cos 0 · 2 5 =
3
A
小试牛刀
(1)如图①②,锐角的正弦值和余弦值都随着锐角的变化而变
化.试探索随着锐角度数的增大,它的正弦值和余弦值变化
的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°
这些锐角的正弦值的大小和余弦值的大小.
小试牛刀
(3)比较大小(在横线上填写“<”“>”或“=”):
若α=45°,则sin α________cos α;
若α<45°,则sin α________cos α;
若α>45°,则sin α________cos α.
(4)利用互为余角的两个角的正弦值和余弦值的关系,试比
较下列正弦值和余弦值的大小:sin 10°,cos 30°,
sin 50°,cos 70°.
(1)锐角的正弦值随角度的增大而增大,余弦值随角度的
增大而减小.
(2)sin 18°cos 88°(4)sin 10°解:
<
=
>
小试牛刀
5 如图,已知∠ABC 和射线BD 上一点P (点P 与点B 不重合,
且点P 到BA,BC 的距离分别为PE,PF 的长).
(1)若∠EBP=40°,∠FBP=20°,试比较PE,PF 的大小;
(2)若∠EBP=α,∠FBP=β,α,β 都是锐角,且α>β,
请比较PE,PF 的大小.
小试牛刀
(1)∵PE⊥AB,PF⊥BC,
∴sin ∠EBP= =sin 40°,sin ∠FBP= =
sin 20°.又∵sin 40°>sin 20°,
∴ > ,∴PE>PF.
(2)∵α,β 都是锐角,且α>β,∴sin α>sin β.
又∵sin ∠EBP= =sin α,sin ∠FBP= =sin β,
∴ > ,∴PE>PF.
解:
小试牛刀
如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交
于点D,E,F,G,已知∠CGD=42°.
(1)求∠CEF 的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC 边于
点H,如图②所示,点H,B 在直尺上的读数分别为4,13.4,求BC
的长(结果保留两位小数).
(参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)
小试牛刀
(1)∵∠CGD=42°,∠C=90°,∴∠CDG=90°-42°=48°.
∵DG∥EF,∴∠CEF=∠CDG=48°.
(2)∵点H,B 的读数分别为4,13.4,∴HB=13.4-4=9.4(cm), ∴BC=HB cos 42°≈9.4×0.74≈6.96(cm).
答:BC 的长约为6.96 cm.
解:
小试牛刀
如图,一艘海轮在A点时测得灯塔C 在它的北偏东42°方向上,它沿正东方向航行80海里后到达B 处,此时灯塔C 在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C 的最短距离(结果精确到0.1);
(2)求海轮在B 处时与灯塔C 的距离(结果保留整数).
(参考数据:sin 55°≈0.819,cos 55°≈0.574,
tan 55°≈1.428,tan 42°≈0.900,
tan 35°≈0.700,tan 48°≈1.111)
小试牛刀
解:
(1)如图,过C 作AB 的垂线,垂足为D,
根据题意可得:∠ACD=42°,∠BCD
=55°.设CD 的长为x海里,
在Rt△ACD 中,tan 42°= ,则AD=x · tan 42°海里,
在Rt△BCD 中,tan 55°= ,则BD=x · tan 55°海里.
∵AB=80海里,∴AD+BD=80海里,
∴x · tan 42°+x · tan 55°=80,解得x ≈ 34.4,
即海轮在航行过程中与灯塔C 的最短距离约是34.4海里.
(2)在Rt△BCD 中,cos 55°= ,
∴BC= ≈60(海里),
即海轮在B 处时与灯塔C 的距离约是60海里.
课堂小结
1.利用计算器可求锐角的三角函数值,按键顺序为:
先按 键或 键或 键,再按角度值,
最后按 键就可求出相应的三角函数值.
2.已知锐角三角函数值也可求相应的锐角,按键顺
序为:先按 键,再按 键或 键或
键,然后输入三角函数值,最后按 键
就可求出相应角度.
课堂小结
sin
sin
cos
cos
tan
tan
2nd F
=
=
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.1 锐角三角函数
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
要测量教学楼的高度,小英身高1.6m.她在距离教学楼30m处测得仰角为25°,你能借助计算器估算出教学楼的高度吗 (精确到0.1m)
新课精讲
探索新知
1
知识点
用计算器求已知锐角的三角函数值
通过上面的学习,我们知道,当锐角A 是30°,45°或60°等特殊角时,可以求得这些特殊角的 锐角三角函数值;如果锐角A 不是这些特殊角, 怎样得到它的锐角三角函数值呢?
我们可以借助计算器求锐角三角函数值.
例如求sin18°,利用计算器的 键,并输入角度值18,
得到结果sin18°=0.309 016 994.
又如求tan30°36′,利用 键,并输入角的度、分值(可以使用 键),就可以得到结果0.591 398 351.
因为30°36′=30.6°,所以也可以利用 键,并输入角度值30.6,同样得到结果0.591 398 351.
探索新知
sin
tan
°′ ″
tan
探索新知
归 纳
利用计算器求锐角三角函数值:
1. 当锐角的大小以度为单位时,可先按 , ,
键,然后输入角度值(可以是整数,也可以是
小数),最后按 键,就可以在显示屏上显示出
结果;
2. 当锐角的大小以度、分、秒为单位时要借助
键计算,按键顺序是: (或 、 )、度数、
、分数、 、秒数、 、 .
sin
cos
tan
=
°′ ″
sin
cos
tan
°′ ″
°′ ″
°′ ″
=
探索新知
例1 用计算器求sin 16°,cos 42°,tan 85°,
sin 72°38′25″的值.
解:如下表:
按键顺序 显示结果
sin 16° 0.275 637 355
cos 42° 0.743 144 825
tan 85° 11.430 052 3
sin 72°38′25″ 0.954 450 312
sin
tan
sin
1
6
4
cos
2
8
5
2
5
2
7
3
8
=
=
=
=
°′ ″
°′ ″
°′ ″
探索新知
总 结
要注意不同型号的计算器的操作步骤可能有所不同.
典题精讲
1 用计算器求下列锐角三角函数值:
(1)sin 20°,cos 70°; sin 35°, cos 55°;
sin15°32′,cos74°28′;
(2)tan 3° 8',tan 80° 25′43".
(1)sin 20°≈0.342 0,cos 70°≈0.342 0;
sin 35°≈0.573 6,cos 55°≈0.573 6;
sin 15°32′≈0.267 8,cos 74°28′≈0.267 8.
(2)tan 3°8′≈0.054 7,tan 80°25′43″≈5.930 4.
解:
典题精讲
如图,是我们数学课上采用的科学计算器面板,利用该型号计算器计算 cos 55°,按键顺序正确的是( )
A.
B.
C.
D.
利用计算器求sin 30°时,依次按键
,则计算器上显示的结果是( )
A.0.5 B.0.707 C.0.866 D.1
sin
3
0
°′ ″
=
cos
2
5
5
×
=
cos
2
5
5
0
=
cos
2
5
5
=
cos
2
5
5
=
C
A
探索新知
2
知识点
用计算器求已知三角函数值的对应角
如果已知锐角三角函数值,也可以使用计算器求出相应锐角的度数.
例如,已知sin A=0. 501 8,用计算器求锐角A 可以按照下面方法操作:
依次按键 ,然后输入函数值0.501 8,得到∠A=30.119 158 67° (这说明锐角A精确到1°的结果为30°).
sin
2nd F
探索新知
还可以利用 键,进一步得到∠A=
30 °07′08.97″(这说明锐角A 精确到1′的结果为30°7′,精确到 1"的结果为30°7′9″).
2nd F
°′ ″
探索新知
归 纳
已知锐角三角函数值求锐角的度数:
如果是特殊角(30°, 45°,60°)的三角函数值,可直接写出其相应的角的度数;若不是特殊角的三角函数值,应利用计算器求角的度数.求角的度数要先按 键,将 、 、 转化成它们的第二功能键;当三角函数值为分数时,应先化成小数.
2nd F
sin
cos
tan
探索新知
例2 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sin A=0.516 8(结果精确到0.01°);
(2)cos A=0.675 3(结果精确到1″);
(3)tan A=0.189(结果精确到1°).
导引:已知锐角三角函数值,利用计算器求锐
角的度数时要注意先按 键.
2nd F
探索新知
解:(1)依次按键:
显示结果为:31.117 845 56,∠A≈31.12°.
(2)依次按键:
显示结果为:47°31′21.18″,
即 ∠A≈47°31′21″.
(3)依次按键:
显示结果为:10.702 657 49,即∠A≈11°.
sin
2nd F
0
5
1
6
8
=
,
2nd F
tan
0
9
1
8
=
,
2nd F
°′ ″
cos
0
3
7
6
5
=
2nd F
,
探索新知
总 结
计算器直接计算出的角的单位是度,而不是度、分、秒,因此若要得到用度、分、秒表示的角度,可以借助 和 键.
2nd F
°′ ″
典题精讲
已知下列锐角三角函数值,用计算器求其相应锐角的度数:
(1)sin A= 0. 627 5,sin B= 0.054 7;
(2)cos A= 0. 625 2,cos B= 0. 165 9;
(3)tan A= 4. 842 5,tan B= 0.881 6.
(1)∠A≈38°51′57″,∠B≈3°8′8″;
(2)∠A≈51°18′11″,∠B≈80°27′2″;
(3)∠A≈78°19′56″,∠B≈41°23′58″.
解:
典题精讲
已知α 为锐角,且tan α=3.387,下列各值中与α 最接近的是( )
A.73°33′ B.73°27′
C.16°27′ D.16°21′
在△ABC 中,∠C=90°,BC=5,AB=13,用科学计算器求∠A 约等于( )
A.24°38′ B.65°22′
C.67°23′ D.22°37′
2
3
A
D
探索新知
3
知识点
用计算器探究三角函数的性质
用计算器求下列各组锐角的三角函数值,从中你能
得出什么猜想?
(1)sin83°,cos7°;
(2)sin56°,cos34°;
(3) sin27°36′ , cos62°24′.
探索新知
2.用计算器求下列各组锐角的三角函数值,从中你能
得出什么猜想?
(1)sin13°, sin25°,sin36°,sin44° , sin57°,
sin68°, sin79°17′,sin83°27′53″;
(2)cos17°34′,cos34°27′53″,cos53°18′ ,
cos69°57′ 3″,cos77°17′ ,cos88°17′25″;
(3)tan27°34′,tan43°57′28″,tan52°18′15″ ,
tan67°,tan78°17′,tan85°24′ .
探索新知
1. 猜想:sin = cos(90°- ).
2. (1)猜想:对于锐角A,它的正弦函数 (sinA)的函数值随
自变量锐角A 的增大而增大,且sinA必满足 0 < sinA<1.
(2)猜想:对于锐角A,它的余弦函数(cosA)的函数值随锐角
A 的增大而减小,且cosA 必满足0 < cosA < 1.
(3)猜想:对于锐角A,它的正切函数(tanA)的函数值随锐角
A 的增大而增大 , 且tanA 满足0 < tanA.
探索新知
归 纳
(1)sin = cos(90°- ).
(2)对于锐角A,它的正弦函数 (sinA)的函数值随自变
量锐角A 的增大而增大,且sinA必满足0 < sinA<1.
(3)对于锐角A,它的余弦函数(cosA)的函数值随锐
角A 的增大而减小,且cosA 必满足0 < cosA < 1.
(4)对于锐角A,它的正切函数(tanA)的函数值随锐
角A 的增大而增大 , 且tanA 满足0 < tanA.
探索新知
例3 已知α+β=90°. 探究:
(1)sin α 与cos β 的关系;
(2)tan α 与tan β 的关系.
导引:根据α 和β 互余,可以将α 和β 放入同一个直角三角
形中,利用锐角三角函数的定义去探究互为余角的两
角的三角函数关系.
探索新知
解:如图,在Rt△ABC 中,∠C=90°,∠A=α,
∠B=β.
令∠A,∠B,∠C 所对的边分别是a,b,c.
(1)∵sin α= , cos β= ,
∴sin α=cos β.
(2)∵tan α= , tan β= ,
∴tan α · tan β=1.
探索新知
总 结
互为余角的两角的三角函数间的关系:
(1)任意锐角的正弦值等于它的余角的余弦值,即
sin α=cos (90°-α )或cos α=sin (90°-α );
(2)任意锐角的正切值与它的余角的正切值互为倒
数,即tan α · tan (90°-α )=1.
典题精讲
1 在Rt△ABC 中,∠C=90°,下列各式中正确的是( )
A.sin A=sin B B.tan A=tan B
C.sin A=cos B D.cos A=cos B
C
用计算器比较tan 25°,sin 27°,cos 26°的大小关系是( )
A.tan 25°
C
典题精讲
用计算器求sin 15°,sin 25°,sin 35°,sin 45°,sin 55°,sin 65°,sin 75°,sin 85°的值,研究sin α的值随锐角α变化的规律,根据这个规律判断:若
C.0°<α<60° D.60°<α<90°
3
A
易错提醒
用计算器求sin 35°29′的值(结果精确到0.001).
解:
sin 35°29′≈0.580.
易错点:不区分35°29′与35.29°而导致错误.
学以致用
小试牛刀
用计算器计算cos 44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
用计算器验证,下列等式正确的是( )
A.sin 18°24′+sin 35°36′=sin 54°
B.sin 65°54′-sin 35°54′=sin 30°
C.2sin 15°30′=sin 31°
D.sin 72°18′-sin 12°18′=sin 47°42′
1
B
2
D
小试牛刀
为了方便行人推车过某天桥,市政府在10 m高的天桥一侧修建了40 m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A. 2ndF sin 0 · 2 5 =
B. sin 2ndF 0 · 2 5 =
C. sin 0 · 2 5 =
D. 2ndF cos 0 · 2 5 =
3
A
小试牛刀
(1)如图①②,锐角的正弦值和余弦值都随着锐角的变化而变
化.试探索随着锐角度数的增大,它的正弦值和余弦值变化
的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°
这些锐角的正弦值的大小和余弦值的大小.
小试牛刀
(3)比较大小(在横线上填写“<”“>”或“=”):
若α=45°,则sin α________cos α;
若α<45°,则sin α________cos α;
若α>45°,则sin α________cos α.
(4)利用互为余角的两个角的正弦值和余弦值的关系,试比
较下列正弦值和余弦值的大小:sin 10°,cos 30°,
sin 50°,cos 70°.
(1)锐角的正弦值随角度的增大而增大,余弦值随角度的
增大而减小.
(2)sin 18°
<
=
>
小试牛刀
5 如图,已知∠ABC 和射线BD 上一点P (点P 与点B 不重合,
且点P 到BA,BC 的距离分别为PE,PF 的长).
(1)若∠EBP=40°,∠FBP=20°,试比较PE,PF 的大小;
(2)若∠EBP=α,∠FBP=β,α,β 都是锐角,且α>β,
请比较PE,PF 的大小.
小试牛刀
(1)∵PE⊥AB,PF⊥BC,
∴sin ∠EBP= =sin 40°,sin ∠FBP= =
sin 20°.又∵sin 40°>sin 20°,
∴ > ,∴PE>PF.
(2)∵α,β 都是锐角,且α>β,∴sin α>sin β.
又∵sin ∠EBP= =sin α,sin ∠FBP= =sin β,
∴ > ,∴PE>PF.
解:
小试牛刀
如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交
于点D,E,F,G,已知∠CGD=42°.
(1)求∠CEF 的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC 边于
点H,如图②所示,点H,B 在直尺上的读数分别为4,13.4,求BC
的长(结果保留两位小数).
(参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)
小试牛刀
(1)∵∠CGD=42°,∠C=90°,∴∠CDG=90°-42°=48°.
∵DG∥EF,∴∠CEF=∠CDG=48°.
(2)∵点H,B 的读数分别为4,13.4,∴HB=13.4-4=9.4(cm), ∴BC=HB cos 42°≈9.4×0.74≈6.96(cm).
答:BC 的长约为6.96 cm.
解:
小试牛刀
如图,一艘海轮在A点时测得灯塔C 在它的北偏东42°方向上,它沿正东方向航行80海里后到达B 处,此时灯塔C 在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C 的最短距离(结果精确到0.1);
(2)求海轮在B 处时与灯塔C 的距离(结果保留整数).
(参考数据:sin 55°≈0.819,cos 55°≈0.574,
tan 55°≈1.428,tan 42°≈0.900,
tan 35°≈0.700,tan 48°≈1.111)
小试牛刀
解:
(1)如图,过C 作AB 的垂线,垂足为D,
根据题意可得:∠ACD=42°,∠BCD
=55°.设CD 的长为x海里,
在Rt△ACD 中,tan 42°= ,则AD=x · tan 42°海里,
在Rt△BCD 中,tan 55°= ,则BD=x · tan 55°海里.
∵AB=80海里,∴AD+BD=80海里,
∴x · tan 42°+x · tan 55°=80,解得x ≈ 34.4,
即海轮在航行过程中与灯塔C 的最短距离约是34.4海里.
(2)在Rt△BCD 中,cos 55°= ,
∴BC= ≈60(海里),
即海轮在B 处时与灯塔C 的距离约是60海里.
课堂小结
1.利用计算器可求锐角的三角函数值,按键顺序为:
先按 键或 键或 键,再按角度值,
最后按 键就可求出相应的三角函数值.
2.已知锐角三角函数值也可求相应的锐角,按键顺
序为:先按 键,再按 键或 键或
键,然后输入三角函数值,最后按 键
就可求出相应角度.
课堂小结
sin
sin
cos
cos
tan
tan
2nd F
=
=
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
