【班海精品】人教版(新)九下-28.1 锐角三角函数 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-28.1 锐角三角函数 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览










文档简介
(共41张PPT)
28.1 锐角三角函数
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
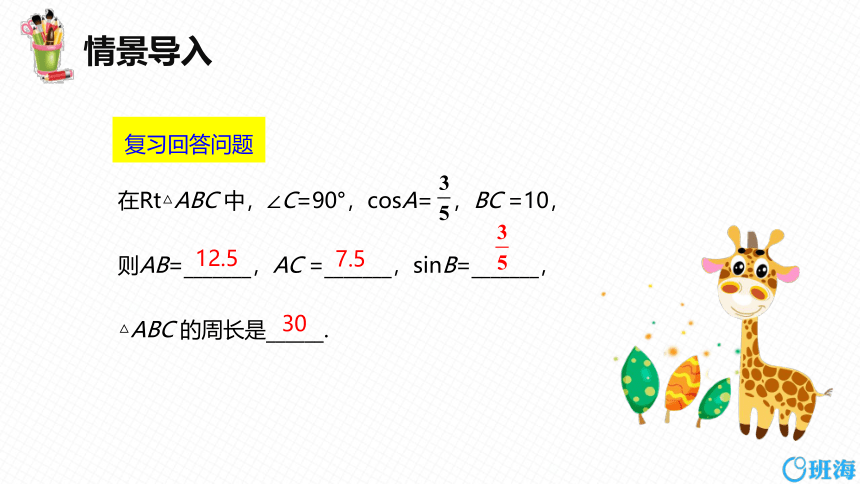
复习回答问题
在Rt△ABC 中,∠C=90°,cosA= ,BC =10,
则AB=_______,AC =_______,sinB=_______,
△ABC 的周长是______.
12.5
7.5
30
新课精讲
探索新知
1
知识点
特殊角(30°,45°,60°)的三角函数值
为了测量一棵大树的高度,准备了如下测量工具:
①含30°和60°两个锐角的三角尺;
②皮尺. 请你设计一个测量方案,测出一棵大树
的高度. 你会吗?还是学习本节知识吧,学后
你会胸有成竹的,你还等什么?
探索新知
探究:
两块三角尺(如图)中有几个不同的锐角?这几个锐角的正弦值、余弦值和正切值各是多少?
探索新知
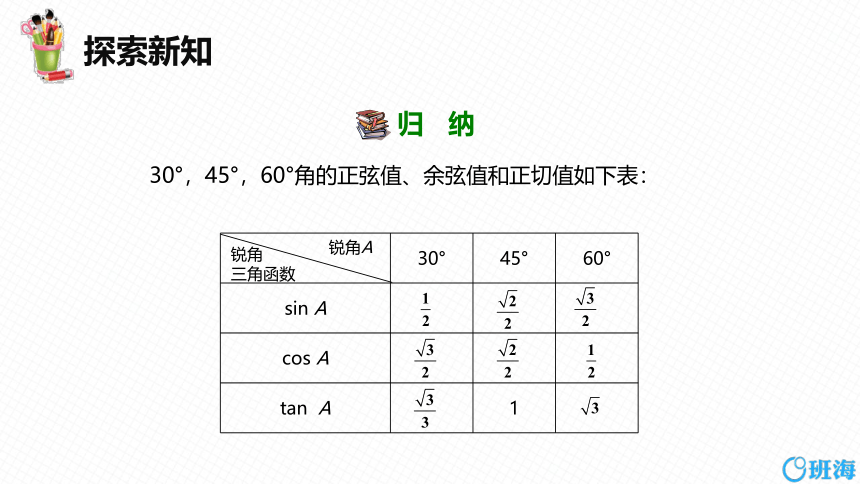
归 纳
30°,45°,60°角的正弦值、余弦值和正切值如下表:
30° 45° 60°
sin A
cos A
tan A 1
锐角A
锐角
三角函数
探索新知
例1 求下列各式的值:
(1)cos260°+sin260°;
(2)
解: (1) cos260°+sin260°
=1;
(2)
=0.
探索新知
总 结
有关特殊角的三角函数值的计算,先直接写出三角函数值,将运算转化为实数的混合运算,然后根据实数的运算法则计算.
典题精讲
1 求下列各式的值:
(1) 1-2sin 30°cos 30°;
(2) 3tan 30°-tan 45°+ 2sin 60°;
(3) (cos230°+sin230°) ×tan 60°.
解:
典题精讲
cos60°的值等于( )
A. B. 1 C. D.
下列运算:sin 30°= , =2 ,π0=π,
2-2=-4,其中运算结果正确的个数为( )
A.4 B.3 C.2 D.1
2
3
D
D
典题精讲
计算sin245°+cos 30°·tan 60°,其结果是( )
A.2 B.1 C. D.
下列各式中正确的是( )
A.sin 60°=
B.cos 45°+sin 45°=
C.sin 60°=sin(2×30°)=2sin 30°
D.tan 60°+tan 30°=2
4
5
B
A
探索新知
2
知识点
特殊三角函数值的对应角
在Rt△ABC 中,∠C=90°,BC= ,AC= ,求∠A、∠B 的度数.
∵tanA=
∴∠A=30°,∠B=60°.
探索新知
归 纳
根据一个锐角的特殊的三角函数值,也可以求出角的度数.
探索新知
例2 (1)如图(1),在Rt△ABC中,∠C=90°, AB= ,
BC= ,求∠A 的度数.
(2)如图(2),AO 是圆锥的高,OB 是底面半径,
AO= OB,求 的度数.
探索新知
解: (1)在图(1)中,
(2)在图(2)中,
典题精讲
在Rt△ABC,∠C=90°,BC= ,AC= ,
就∠A,∠B 的度数.
解:
在Rt△ABC 中,∠C=90°,
所以∠A=30°,
所以∠B=90°-∠A=60°.
典题精讲
在△ABC 中,∠A,∠B 都是锐角,且sin A= ,
cos B= ,则△ABC 的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
已知α,β 均为锐角,且满足
则α+β=________.
2
3
B
75°
探索新知
3
知识点
锐角三角函数间的关系
(1)求特殊锐角的三角函数值的关键是先把它转化为实数
的运算,再根据实数的运算法则计算.
(2)求锐角的度数的关键是先求其正弦值或余弦值或正切
值,然后对应特殊锐角的三角函数值求角的度数.
(3)当A、B 均为锐角时,若A≠B,则sinA≠sinB,
cosA≠cosB,tanA≠tanB.
(4)sin2α+cos2α=1,tanα=
探索新知
例3 已知∠A为锐角,sin A= ,求∠A 的其他三角函数值.
导引:根据sin2 A+cos2 A=1,求出cos A 的值,
然后根据tan A= ,求出tan A 的值.
探索新知
解:∵sin A= ,sin2 A+cos2 A=1,
∴ +cos2 A=1,
∴cos2 A=1-
∴cos A= (负值舍去).
∴
典题精讲
在Rt△ABC 中,∠C=90°,下列式子不一定成立的是( )
A.tan A= B.sin2 A+cos2 A=1
C.sin2 A+sin2 B=1 D.tan A · tan B=1
1
A
2 在Rt△ABC 中,∠C=90°,若sin A= ,则cos B 的值是( )
A. B.
C. D.
B
典题精讲
当45°< ∠A <90°时,下列不等式中正确的是( )
A.tan A>cos A>sin A
B.cos A>tan A>sin A
C.sin A>tan A>cos A
D.tan A>sin A>cos A
3
D
过点C 作CD⊥AB 于点D,如图所示.
在Rt△ADC 中,∵cos A= ,sin A= ,∴AD=AC
·cos A=1×cos 60°= ,CD=AC · sin A=1×sin 60°
= .在Rt△BDC 中,BD=AB-AD=2- = ,∴BC
易错提醒
如图,在△ABC 中,AC=1,AB=2,
∠A=60°,求BC 的长.
解:
易错提醒
错解:在△ABC 中,∵ =sin A,∴BC=AB · sin A=
2sin 60°=2× = .
诊断:错解的原因是忽略了锐角三角函数使用的前提是在
直角三角形中.本题中没有明确指出△ABC 是直角
三角形,因此,不能直接得到 =sin A,必须通
过添加辅助线构造出直角三角形,再利用三角函数
的定义来解决.
易错点:忽视锐角的三角函数值是在直角三角形中求出这一条件而致错.
学以致用
小试牛刀
如图,△ABC 内接于⊙O,AB,CD 为⊙O 的直径,DE⊥AB 于点E,sin A= ,则∠D 的度数是________.
1
30°
小试牛刀
如图,点A,B,C 在⊙O上,∠ACB=30°,则sin∠AOB的值是( )
A.
B.
C.
D.
2
C
小试牛刀
菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC=45°,OC= ,则点B的坐标为( )
A.( ,1)
B.(1, )
C.( +1,1)
D.(1, +1)
3
C
小试牛刀
4 求下列各式的值:
(1)cos2 45°+tan 60°·sin 60°;
解:
(1)原式=
(2) -cos 30°·tan 30°;
(2)原式=
小试牛刀
(3)sin 30°-cos2 45°+tan2 30°+sin2 60°-cos 60°.
(3)原式=
小试牛刀
5 如图①②③,根据图中数据完成填空,再按要求答题:
sin2A1+sin2B1=_______;sin2A2+sin2B2=________;
sin2A3+sin2B3=________.
(1)观察上述等式,猜想:在Rt△ABC 中,∠C=90°,
都有sin2A+sin2B=________.
1
1
1
1
小试牛刀
(2)如图④,在Rt△ABC 中,∠C=90°,∠A,∠B,∠C 的对
边分别是a,b,c,利用三角函数的定义和勾股定理,证
明你的猜想.
(3)已知:∠A+∠B=90°,且sin A= ,求sin B.
(2)证明:∵sin A= ,sin B= ,a 2+b 2=c 2,
∴sin2 A+sin2 B= =1.
(3)解:∵sin A= ,sin2 A+sin2 B=1,
∴sin B= .
小试牛刀
数学拓展课程《玩转学具》课堂中,小陆同学发现,一副三角尺中,
含45°的三角尺的斜边与含30°的三角尺的长直角边相等,于是,小陆
同学提出一个问题,如图,将一副三角尺直角顶点重合拼放在一起,
点B,C,E在同一直线上,若BC=2,求AF的长.请你运用所学的数
学知识解决这个问题.
小试牛刀
解:
在Rt△ABC 中,BC=2,∠A=30°,AC= =2 ,
则EF=AC= 2 ,∵∠E=45°,
∴FC=EF · sin E= ,
∴AF=AC-FC=2 - .
小试牛刀
如图,直线y=- x+b 与x 轴、y 轴分别交于D,A 两点,
与双曲线y= 在第一象限交于B,C 两点,且AB · AC=4.求:
(1)∠ADO 的度数;(2)k 的值.
解:
(1)易知A (0,b),D (b,0),
∴AO=b,DO= b. ∴tan ∠ADO= ,
∴∠ADO=30°.
小试牛刀
(2)如图,过B 作BM⊥y 轴于M,过C 作CN⊥y 轴于N.
设点B 和点C 的横坐标分别为m,n,
则AB= ,AC= ,
∴AB·AC= =4,
∴mn=3.又∵m,n 为方程- x+b= 的两根,
∴mn= k,∴3= k,∴k= .
课堂小结
课堂小结
30° 45° 60°
sin A
cos A
tan A 1
特殊角的三角函数值:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.1 锐角三角函数
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回答问题
在Rt△ABC 中,∠C=90°,cosA= ,BC =10,
则AB=_______,AC =_______,sinB=_______,
△ABC 的周长是______.
12.5
7.5
30
新课精讲
探索新知
1
知识点
特殊角(30°,45°,60°)的三角函数值
为了测量一棵大树的高度,准备了如下测量工具:
①含30°和60°两个锐角的三角尺;
②皮尺. 请你设计一个测量方案,测出一棵大树
的高度. 你会吗?还是学习本节知识吧,学后
你会胸有成竹的,你还等什么?
探索新知
探究:
两块三角尺(如图)中有几个不同的锐角?这几个锐角的正弦值、余弦值和正切值各是多少?
探索新知
归 纳
30°,45°,60°角的正弦值、余弦值和正切值如下表:
30° 45° 60°
sin A
cos A
tan A 1
锐角A
锐角
三角函数
探索新知
例1 求下列各式的值:
(1)cos260°+sin260°;
(2)
解: (1) cos260°+sin260°
=1;
(2)
=0.
探索新知
总 结
有关特殊角的三角函数值的计算,先直接写出三角函数值,将运算转化为实数的混合运算,然后根据实数的运算法则计算.
典题精讲
1 求下列各式的值:
(1) 1-2sin 30°cos 30°;
(2) 3tan 30°-tan 45°+ 2sin 60°;
(3) (cos230°+sin230°) ×tan 60°.
解:
典题精讲
cos60°的值等于( )
A. B. 1 C. D.
下列运算:sin 30°= , =2 ,π0=π,
2-2=-4,其中运算结果正确的个数为( )
A.4 B.3 C.2 D.1
2
3
D
D
典题精讲
计算sin245°+cos 30°·tan 60°,其结果是( )
A.2 B.1 C. D.
下列各式中正确的是( )
A.sin 60°=
B.cos 45°+sin 45°=
C.sin 60°=sin(2×30°)=2sin 30°
D.tan 60°+tan 30°=2
4
5
B
A
探索新知
2
知识点
特殊三角函数值的对应角
在Rt△ABC 中,∠C=90°,BC= ,AC= ,求∠A、∠B 的度数.
∵tanA=
∴∠A=30°,∠B=60°.
探索新知
归 纳
根据一个锐角的特殊的三角函数值,也可以求出角的度数.
探索新知
例2 (1)如图(1),在Rt△ABC中,∠C=90°, AB= ,
BC= ,求∠A 的度数.
(2)如图(2),AO 是圆锥的高,OB 是底面半径,
AO= OB,求 的度数.
探索新知
解: (1)在图(1)中,
(2)在图(2)中,
典题精讲
在Rt△ABC,∠C=90°,BC= ,AC= ,
就∠A,∠B 的度数.
解:
在Rt△ABC 中,∠C=90°,
所以∠A=30°,
所以∠B=90°-∠A=60°.
典题精讲
在△ABC 中,∠A,∠B 都是锐角,且sin A= ,
cos B= ,则△ABC 的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
已知α,β 均为锐角,且满足
则α+β=________.
2
3
B
75°
探索新知
3
知识点
锐角三角函数间的关系
(1)求特殊锐角的三角函数值的关键是先把它转化为实数
的运算,再根据实数的运算法则计算.
(2)求锐角的度数的关键是先求其正弦值或余弦值或正切
值,然后对应特殊锐角的三角函数值求角的度数.
(3)当A、B 均为锐角时,若A≠B,则sinA≠sinB,
cosA≠cosB,tanA≠tanB.
(4)sin2α+cos2α=1,tanα=
探索新知
例3 已知∠A为锐角,sin A= ,求∠A 的其他三角函数值.
导引:根据sin2 A+cos2 A=1,求出cos A 的值,
然后根据tan A= ,求出tan A 的值.
探索新知
解:∵sin A= ,sin2 A+cos2 A=1,
∴ +cos2 A=1,
∴cos2 A=1-
∴cos A= (负值舍去).
∴
典题精讲
在Rt△ABC 中,∠C=90°,下列式子不一定成立的是( )
A.tan A= B.sin2 A+cos2 A=1
C.sin2 A+sin2 B=1 D.tan A · tan B=1
1
A
2 在Rt△ABC 中,∠C=90°,若sin A= ,则cos B 的值是( )
A. B.
C. D.
B
典题精讲
当45°< ∠A <90°时,下列不等式中正确的是( )
A.tan A>cos A>sin A
B.cos A>tan A>sin A
C.sin A>tan A>cos A
D.tan A>sin A>cos A
3
D
过点C 作CD⊥AB 于点D,如图所示.
在Rt△ADC 中,∵cos A= ,sin A= ,∴AD=AC
·cos A=1×cos 60°= ,CD=AC · sin A=1×sin 60°
= .在Rt△BDC 中,BD=AB-AD=2- = ,∴BC
易错提醒
如图,在△ABC 中,AC=1,AB=2,
∠A=60°,求BC 的长.
解:
易错提醒
错解:在△ABC 中,∵ =sin A,∴BC=AB · sin A=
2sin 60°=2× = .
诊断:错解的原因是忽略了锐角三角函数使用的前提是在
直角三角形中.本题中没有明确指出△ABC 是直角
三角形,因此,不能直接得到 =sin A,必须通
过添加辅助线构造出直角三角形,再利用三角函数
的定义来解决.
易错点:忽视锐角的三角函数值是在直角三角形中求出这一条件而致错.
学以致用
小试牛刀
如图,△ABC 内接于⊙O,AB,CD 为⊙O 的直径,DE⊥AB 于点E,sin A= ,则∠D 的度数是________.
1
30°
小试牛刀
如图,点A,B,C 在⊙O上,∠ACB=30°,则sin∠AOB的值是( )
A.
B.
C.
D.
2
C
小试牛刀
菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC=45°,OC= ,则点B的坐标为( )
A.( ,1)
B.(1, )
C.( +1,1)
D.(1, +1)
3
C
小试牛刀
4 求下列各式的值:
(1)cos2 45°+tan 60°·sin 60°;
解:
(1)原式=
(2) -cos 30°·tan 30°;
(2)原式=
小试牛刀
(3)sin 30°-cos2 45°+tan2 30°+sin2 60°-cos 60°.
(3)原式=
小试牛刀
5 如图①②③,根据图中数据完成填空,再按要求答题:
sin2A1+sin2B1=_______;sin2A2+sin2B2=________;
sin2A3+sin2B3=________.
(1)观察上述等式,猜想:在Rt△ABC 中,∠C=90°,
都有sin2A+sin2B=________.
1
1
1
1
小试牛刀
(2)如图④,在Rt△ABC 中,∠C=90°,∠A,∠B,∠C 的对
边分别是a,b,c,利用三角函数的定义和勾股定理,证
明你的猜想.
(3)已知:∠A+∠B=90°,且sin A= ,求sin B.
(2)证明:∵sin A= ,sin B= ,a 2+b 2=c 2,
∴sin2 A+sin2 B= =1.
(3)解:∵sin A= ,sin2 A+sin2 B=1,
∴sin B= .
小试牛刀
数学拓展课程《玩转学具》课堂中,小陆同学发现,一副三角尺中,
含45°的三角尺的斜边与含30°的三角尺的长直角边相等,于是,小陆
同学提出一个问题,如图,将一副三角尺直角顶点重合拼放在一起,
点B,C,E在同一直线上,若BC=2,求AF的长.请你运用所学的数
学知识解决这个问题.
小试牛刀
解:
在Rt△ABC 中,BC=2,∠A=30°,AC= =2 ,
则EF=AC= 2 ,∵∠E=45°,
∴FC=EF · sin E= ,
∴AF=AC-FC=2 - .
小试牛刀
如图,直线y=- x+b 与x 轴、y 轴分别交于D,A 两点,
与双曲线y= 在第一象限交于B,C 两点,且AB · AC=4.求:
(1)∠ADO 的度数;(2)k 的值.
解:
(1)易知A (0,b),D (b,0),
∴AO=b,DO= b. ∴tan ∠ADO= ,
∴∠ADO=30°.
小试牛刀
(2)如图,过B 作BM⊥y 轴于M,过C 作CN⊥y 轴于N.
设点B 和点C 的横坐标分别为m,n,
则AB= ,AC= ,
∴AB·AC= =4,
∴mn=3.又∵m,n 为方程- x+b= 的两根,
∴mn= k,∴3= k,∴k= .
课堂小结
课堂小结
30° 45° 60°
sin A
cos A
tan A 1
特殊角的三角函数值:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
