【班海精品】人教版(新)九下-28.2 解直角三角形及其应用 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-28.2 解直角三角形及其应用 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览







文档简介
(共33张PPT)
28.2 解直角三角形及其应用
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.解直角三角形的意义:在直角三角形中,由已知元素
求出所有未知元素的过程,叫做直角三角形.
2.直角三角形中诸元素之间的关系:
(1)三边之间的关系:a 2+b 2=c 2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
把∠A 换成∠B 同样适用.
新课精讲
探索新知
1
知识点
借助工具测量的应用
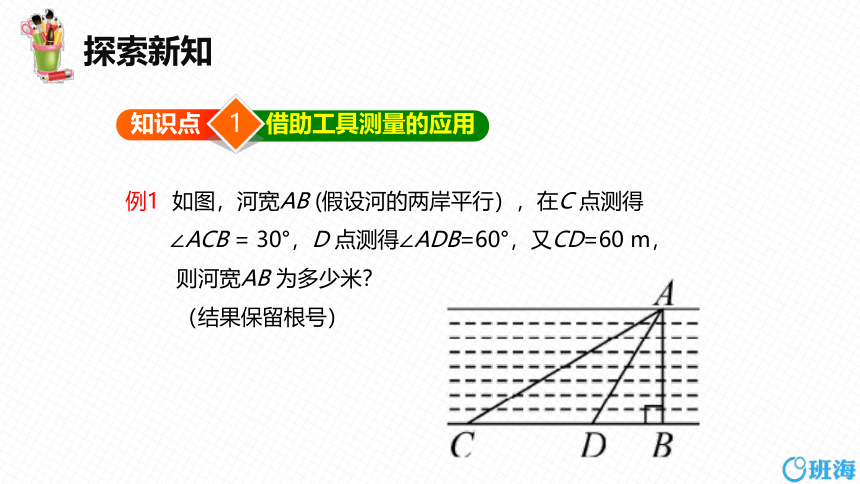
例1 如图,河宽AB (假设河的两岸平行),在C 点测得
∠ACB = 30°,D 点测得∠ADB=60°,又CD=60 m,
则河宽AB 为多少米?
(结果保留根号)
探索新知
分析:先根据三角形外角的性质求出∠CAD 的度数,判
断出△ACD 的形状,再由锐角三角函数的定义即
可求出AB 的值.
解:∵ ∠ACB=30°, ∠ADB=60°,
∴ ∠CAD=30°,
∴AD=CD=60 m,
在Rt△ABD 中,AB=AD · sin∠ADB=60×
典题精讲
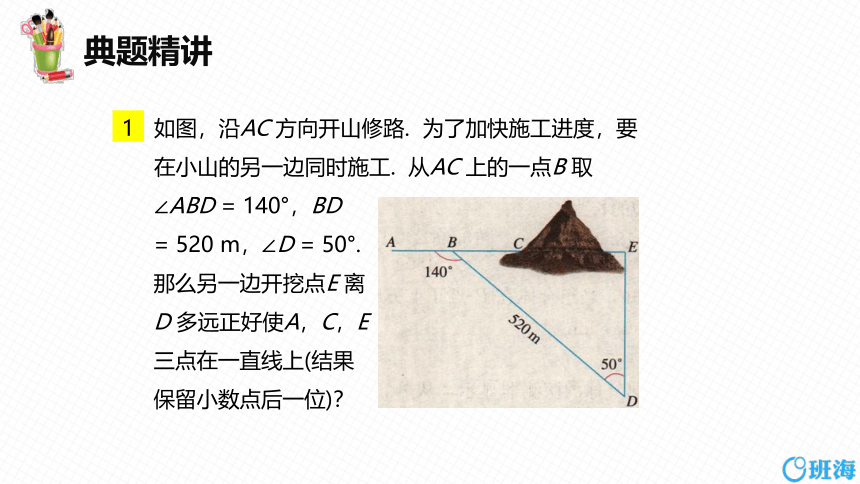
如图,沿AC 方向开山修路. 为了加快施工进度,要在小山的另一边同时施工. 从AC 上的一点B 取∠ABD = 140°,BD
= 520 m,∠D = 50°.
那么另一边开挖点E 离
D 多远正好使A,C,E
三点在一直线上(结果
保留小数点后一位)?
典题精讲
由题意,可知∠DBE=40°,
故∠E=180°-∠D-∠DBE
=180°-50°-40°=90°.
在Rt△BDE 中,cos D= ,
所以DE=BD · cos D=520×cos 50°≈334.2(m).
答:另一边开挖点E 离D 约334.2 m正好使A,C,
E 三点在一直线上.
解:
典题精讲
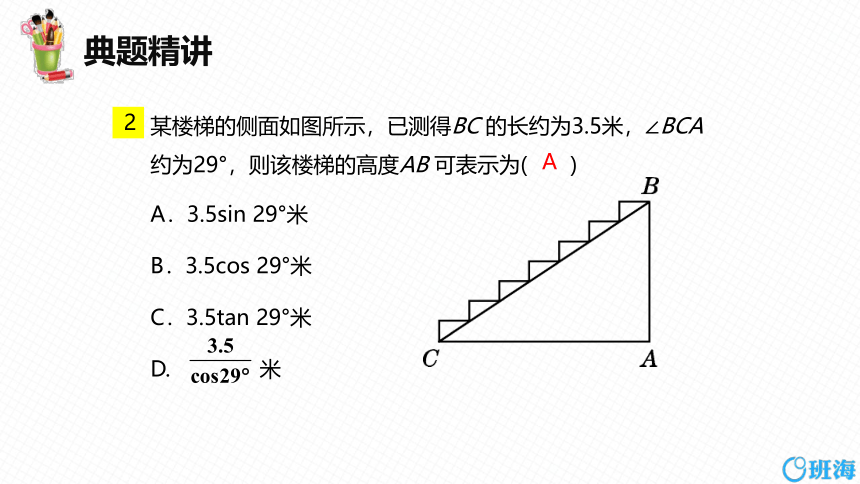
某楼梯的侧面如图所示,已测得BC 的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB 可表示为( )
A.3.5sin 29°米
B.3.5cos 29°米
C.3.5tan 29°米
D. 米
2
A
典题精讲
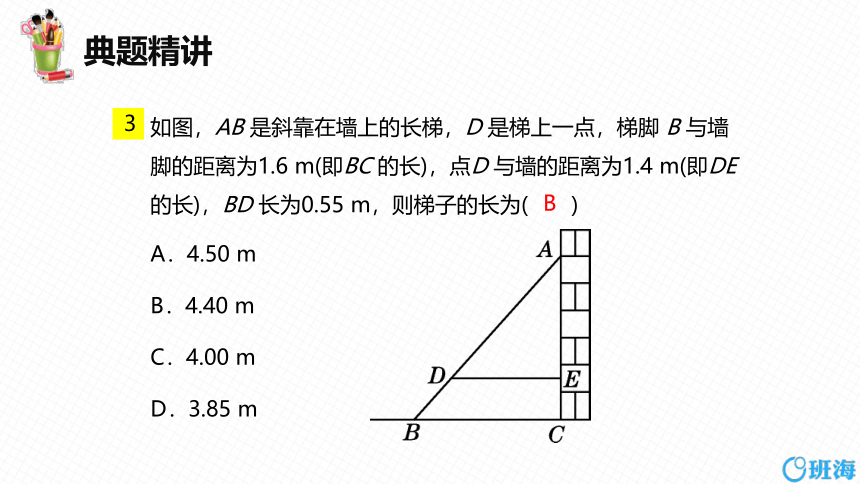
如图,AB 是斜靠在墙上的长梯,D 是梯上一点,梯脚 B 与墙脚的距离为1.6 m(即BC 的长),点D 与墙的距离为1.4 m(即DE 的长),BD 长为0.55 m,则梯子的长为( )
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
3
B
探索新知
2
知识点
借助影子测量的应用
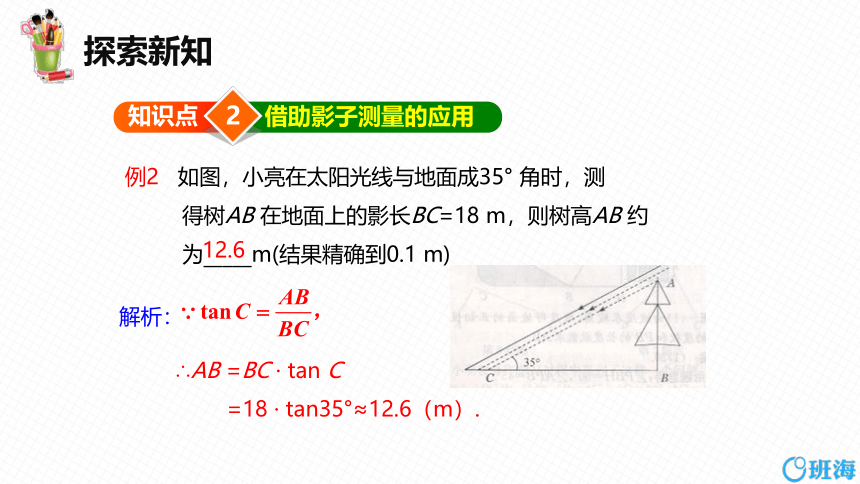
例2 如图,小亮在太阳光线与地面成35° 角时,测
得树AB 在地面上的影长BC=18 m,则树高AB 约
为_____m(结果精确到0.1 m)
∴AB =BC · tan C
=18 · tan35°≈12.6(m).
12.6
解析:
探索新知
总 结
方法指导把实际问题转化为三角形问题,构造直角三角形,寻找解直角三角形所需要的角、边等已知量,解直角三角形,求出实际问题中的未知量.
典题精讲
如图,AB 是伸缩式遮阳棚,CD 是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB 的长是________米.
(假设夏至的正午时刻阳光
与地平面的夹角为60°)
典题精讲
如图,已知电线杆AB 直立于地面上,它的影子恰好落在土坡的坡面CD 和地面BC 上,如果CD 与地面成45°角,∠A=60°,CD=4m,BC=( )
m,则电线杆AB 的长为__________m .
易错提醒
如图,若要在宽AD 为20米的城南大道两边安装路灯,路灯的灯臂BC 长2米,且与灯柱AB 成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO 与灯臂BC 垂直,当灯罩的轴线CO 通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB 高应该设计为多少米(结果保留根号)
易错提醒
如图,延长OC,AB 交于点P.
∵∠ABC=120°,∴∠PBC=60°.
又∵∠OCB=∠A=90°,∴∠P=30°.
根据题意,OA= AD=10米.∵BC=2米,
∴在Rt△CPB 中,PC=BC · tan 60°=2 米,
PB=2BC=4米.∵∠P=∠P,∠PCB=∠A=90°,
∴△PCB∽△PAO.
∴ . ∴PA= 米.
∴AB=PA-PB=(10-4)米.
因此,路灯的灯柱AB 高应该设计为(10 -4)米.
易错点:不能准确地将实际问题转化为解直角三角形问题.
解:
学以致用
小试牛刀
在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知李明距假山的水平距离BD 为12 m,他的眼睛距地面的高度为1.6 m,李明的视线经过量角器零刻度线OA 和假山的最高点C,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为( )
A.(4 +1.6)m
B.(12 +1.6)m
C.(4 +1.6)m
D.4 m
1
A
小试牛刀
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD (D 为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
2
C
小试牛刀
如图①②分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC 与支架AC 所成的角∠ACB=75°,支架AF 的长为2.50米,篮板顶端F 点到篮框D 的距离FD=1.35米,篮板底部支架HE 与支架AF 所成的角∠FHE=60°,求篮框D 到地面的距离(精确到0.01米).(参考数据:cos 75°≈0.258 8,sin 75°≈0.965 9,tan 75°≈3.732,
≈1.732, ≈1.414)
小试牛刀
解:
如图,延长FE 交CB 于点M,过点A作AG⊥FM 于点G.
在Rt△ABC 中,tan∠ACB= ,
∴AB=BC · tan 75°≈0.60×3.732≈2.239(米).
∴GM=AB ≈2.239米.
在Rt△AGF 中,∵∠FAG=∠FHE=60°,
sin∠FAG= ,即sin 60°= ,
∴FG≈2.165米.
∴DM=FG+GM-DF≈2.165+2.239-1.35≈3.05(米).
因此,篮框D 到地面的距离大约是3.05米.
小试牛刀
如图,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10 m的A处,测得一辆汽车从B 处行驶到C 处所用时间为0.9 s,已知∠B=30°,∠C=45°.
(1)求B,C 之间的距离;(保留根号)
(2)如果此地限速为80 km/h,那么这辆汽车是否超速?
请说明理由.(参考数据: ≈1.7, ≈1.4)
小试牛刀
(1)如图,作AD⊥BC 于D,则AD=10 m. 在Rt△ACD 中,
∵∠C=45°,∴AD=CD=10 m.
在Rt△ABD 中,∵∠B=30°,
∴tan 30°= . ∴BD=AD=10 m.
∴BC=BD+DC=(10+10 ) m,
即B,C 之间的距离为(10+10 ) m.
(2)这辆汽车超速.理由:∵BC=10+10 ≈27(m),
∴汽车速度为 =30(m/s)=108(km/h).
∵108>80,∴这辆汽车超速.
解:
小试牛刀
如图,某办公楼AB 的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A 在地面上的影子F 与墙角C 有25米的距离(B,F,C 在一条直线上).
(1)求办公楼AB 的高度;
(2)若要在A,E 之间挂一些彩旗,
请你求出A,E 之间的距离.
(参考数据:sin 22°≈ ,cos 22°≈ ,tan 22°≈ )
小试牛刀
解:
(1)如图, 过点E 作EM⊥AB,垂足为M.
设AB 为x 米.
在Rt△ABF 中,∠AFB=45°,
∴BF=AB=x 米.∴BC=BF+FC=(x+25)米.
在Rt△AEM 中,∠AEM=22°,AM=AB-BM=AB
-CE=(x-2)米,ME=BC=(x+25)米,
tan22°= ,则 ,
解得x≈20. 即办公楼AB 的高度约为20米.
小试牛刀
(2)由(1)可得ME=x+25≈20+25=45(米).
在Rt△AME 中,cos22°= .
∴AE= =48(米).
即A,E 之间的距离约为48米.
小试牛刀
如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD )靠墙摆放,高
AD=80 cm,宽AB=48 cm,小强身高166 cm,下半身FG=100 cm,
洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成 125°(∠EFG=125°),
脚与洗漱台距离GC=15 cm(点D,C,G,K 在同一直线上).
(1)此时小强头部E 点与地面DK 相距多少?
(2)小强希望他的头部E 恰好在洗漱盆AB 的
中点O 的正上方,他应向前或后退多少?
(sin 80°≈0.98,cos 80°≈0.17, ≈1.41,
结果精确到0.1 cm)
小试牛刀
(1)如图,过点F 作FN⊥DK 于点N,过点E 作EM⊥FN 于点M.
∵EF+FG=166 cm,FG=100 cm,
∴EF=66 cm.
∵∠FGK=80°,
∴FN=100 · sin 80°≈98(cm).
∵∠EFG=125°,
∴∠EFM=180°-125°-10°=45°.
∴FM=66·cos 45°=33 ≈46.53(cm).
∴MN=FN+FM≈98+46.53≈144.5(cm).
∴此时小强头部E 点与地面DK 大约相距144.5 cm.
解:
小试牛刀
(2)如图,过点E 作EP⊥AB 于点P,延长OB 交MN 于点H.
∵AB=48 cm,O 为AB 中点,
∴AO=BO=24 cm.
∵EM=66·sin 45°=33 ≈46.53(cm),
∴PH≈46.53 cm.
∵GN=100·cos 80°≈17(cm),GC=15 cm,
∴OH≈24+15+17=56(cm),
OP=OH-PH≈56-46.53=9.47≈9.5(cm).
∴他应向前约9.5 cm.
课堂小结
课堂小结
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.2 解直角三角形及其应用
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.解直角三角形的意义:在直角三角形中,由已知元素
求出所有未知元素的过程,叫做直角三角形.
2.直角三角形中诸元素之间的关系:
(1)三边之间的关系:a 2+b 2=c 2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
把∠A 换成∠B 同样适用.
新课精讲
探索新知
1
知识点
借助工具测量的应用
例1 如图,河宽AB (假设河的两岸平行),在C 点测得
∠ACB = 30°,D 点测得∠ADB=60°,又CD=60 m,
则河宽AB 为多少米?
(结果保留根号)
探索新知
分析:先根据三角形外角的性质求出∠CAD 的度数,判
断出△ACD 的形状,再由锐角三角函数的定义即
可求出AB 的值.
解:∵ ∠ACB=30°, ∠ADB=60°,
∴ ∠CAD=30°,
∴AD=CD=60 m,
在Rt△ABD 中,AB=AD · sin∠ADB=60×
典题精讲
如图,沿AC 方向开山修路. 为了加快施工进度,要在小山的另一边同时施工. 从AC 上的一点B 取∠ABD = 140°,BD
= 520 m,∠D = 50°.
那么另一边开挖点E 离
D 多远正好使A,C,E
三点在一直线上(结果
保留小数点后一位)?
典题精讲
由题意,可知∠DBE=40°,
故∠E=180°-∠D-∠DBE
=180°-50°-40°=90°.
在Rt△BDE 中,cos D= ,
所以DE=BD · cos D=520×cos 50°≈334.2(m).
答:另一边开挖点E 离D 约334.2 m正好使A,C,
E 三点在一直线上.
解:
典题精讲
某楼梯的侧面如图所示,已测得BC 的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB 可表示为( )
A.3.5sin 29°米
B.3.5cos 29°米
C.3.5tan 29°米
D. 米
2
A
典题精讲
如图,AB 是斜靠在墙上的长梯,D 是梯上一点,梯脚 B 与墙脚的距离为1.6 m(即BC 的长),点D 与墙的距离为1.4 m(即DE 的长),BD 长为0.55 m,则梯子的长为( )
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
3
B
探索新知
2
知识点
借助影子测量的应用
例2 如图,小亮在太阳光线与地面成35° 角时,测
得树AB 在地面上的影长BC=18 m,则树高AB 约
为_____m(结果精确到0.1 m)
∴AB =BC · tan C
=18 · tan35°≈12.6(m).
12.6
解析:
探索新知
总 结
方法指导把实际问题转化为三角形问题,构造直角三角形,寻找解直角三角形所需要的角、边等已知量,解直角三角形,求出实际问题中的未知量.
典题精讲
如图,AB 是伸缩式遮阳棚,CD 是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB 的长是________米.
(假设夏至的正午时刻阳光
与地平面的夹角为60°)
典题精讲
如图,已知电线杆AB 直立于地面上,它的影子恰好落在土坡的坡面CD 和地面BC 上,如果CD 与地面成45°角,∠A=60°,CD=4m,BC=( )
m,则电线杆AB 的长为__________m .
易错提醒
如图,若要在宽AD 为20米的城南大道两边安装路灯,路灯的灯臂BC 长2米,且与灯柱AB 成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO 与灯臂BC 垂直,当灯罩的轴线CO 通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB 高应该设计为多少米(结果保留根号)
易错提醒
如图,延长OC,AB 交于点P.
∵∠ABC=120°,∴∠PBC=60°.
又∵∠OCB=∠A=90°,∴∠P=30°.
根据题意,OA= AD=10米.∵BC=2米,
∴在Rt△CPB 中,PC=BC · tan 60°=2 米,
PB=2BC=4米.∵∠P=∠P,∠PCB=∠A=90°,
∴△PCB∽△PAO.
∴ . ∴PA= 米.
∴AB=PA-PB=(10-4)米.
因此,路灯的灯柱AB 高应该设计为(10 -4)米.
易错点:不能准确地将实际问题转化为解直角三角形问题.
解:
学以致用
小试牛刀
在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知李明距假山的水平距离BD 为12 m,他的眼睛距地面的高度为1.6 m,李明的视线经过量角器零刻度线OA 和假山的最高点C,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为( )
A.(4 +1.6)m
B.(12 +1.6)m
C.(4 +1.6)m
D.4 m
1
A
小试牛刀
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD (D 为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
2
C
小试牛刀
如图①②分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC 与支架AC 所成的角∠ACB=75°,支架AF 的长为2.50米,篮板顶端F 点到篮框D 的距离FD=1.35米,篮板底部支架HE 与支架AF 所成的角∠FHE=60°,求篮框D 到地面的距离(精确到0.01米).(参考数据:cos 75°≈0.258 8,sin 75°≈0.965 9,tan 75°≈3.732,
≈1.732, ≈1.414)
小试牛刀
解:
如图,延长FE 交CB 于点M,过点A作AG⊥FM 于点G.
在Rt△ABC 中,tan∠ACB= ,
∴AB=BC · tan 75°≈0.60×3.732≈2.239(米).
∴GM=AB ≈2.239米.
在Rt△AGF 中,∵∠FAG=∠FHE=60°,
sin∠FAG= ,即sin 60°= ,
∴FG≈2.165米.
∴DM=FG+GM-DF≈2.165+2.239-1.35≈3.05(米).
因此,篮框D 到地面的距离大约是3.05米.
小试牛刀
如图,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10 m的A处,测得一辆汽车从B 处行驶到C 处所用时间为0.9 s,已知∠B=30°,∠C=45°.
(1)求B,C 之间的距离;(保留根号)
(2)如果此地限速为80 km/h,那么这辆汽车是否超速?
请说明理由.(参考数据: ≈1.7, ≈1.4)
小试牛刀
(1)如图,作AD⊥BC 于D,则AD=10 m. 在Rt△ACD 中,
∵∠C=45°,∴AD=CD=10 m.
在Rt△ABD 中,∵∠B=30°,
∴tan 30°= . ∴BD=AD=10 m.
∴BC=BD+DC=(10+10 ) m,
即B,C 之间的距离为(10+10 ) m.
(2)这辆汽车超速.理由:∵BC=10+10 ≈27(m),
∴汽车速度为 =30(m/s)=108(km/h).
∵108>80,∴这辆汽车超速.
解:
小试牛刀
如图,某办公楼AB 的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A 在地面上的影子F 与墙角C 有25米的距离(B,F,C 在一条直线上).
(1)求办公楼AB 的高度;
(2)若要在A,E 之间挂一些彩旗,
请你求出A,E 之间的距离.
(参考数据:sin 22°≈ ,cos 22°≈ ,tan 22°≈ )
小试牛刀
解:
(1)如图, 过点E 作EM⊥AB,垂足为M.
设AB 为x 米.
在Rt△ABF 中,∠AFB=45°,
∴BF=AB=x 米.∴BC=BF+FC=(x+25)米.
在Rt△AEM 中,∠AEM=22°,AM=AB-BM=AB
-CE=(x-2)米,ME=BC=(x+25)米,
tan22°= ,则 ,
解得x≈20. 即办公楼AB 的高度约为20米.
小试牛刀
(2)由(1)可得ME=x+25≈20+25=45(米).
在Rt△AME 中,cos22°= .
∴AE= =48(米).
即A,E 之间的距离约为48米.
小试牛刀
如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD )靠墙摆放,高
AD=80 cm,宽AB=48 cm,小强身高166 cm,下半身FG=100 cm,
洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成 125°(∠EFG=125°),
脚与洗漱台距离GC=15 cm(点D,C,G,K 在同一直线上).
(1)此时小强头部E 点与地面DK 相距多少?
(2)小强希望他的头部E 恰好在洗漱盆AB 的
中点O 的正上方,他应向前或后退多少?
(sin 80°≈0.98,cos 80°≈0.17, ≈1.41,
结果精确到0.1 cm)
小试牛刀
(1)如图,过点F 作FN⊥DK 于点N,过点E 作EM⊥FN 于点M.
∵EF+FG=166 cm,FG=100 cm,
∴EF=66 cm.
∵∠FGK=80°,
∴FN=100 · sin 80°≈98(cm).
∵∠EFG=125°,
∴∠EFM=180°-125°-10°=45°.
∴FM=66·cos 45°=33 ≈46.53(cm).
∴MN=FN+FM≈98+46.53≈144.5(cm).
∴此时小强头部E 点与地面DK 大约相距144.5 cm.
解:
小试牛刀
(2)如图,过点E 作EP⊥AB 于点P,延长OB 交MN 于点H.
∵AB=48 cm,O 为AB 中点,
∴AO=BO=24 cm.
∵EM=66·sin 45°=33 ≈46.53(cm),
∴PH≈46.53 cm.
∵GN=100·cos 80°≈17(cm),GC=15 cm,
∴OH≈24+15+17=56(cm),
OP=OH-PH≈56-46.53=9.47≈9.5(cm).
∴他应向前约9.5 cm.
课堂小结
课堂小结
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
