【班海精品】人教版(新)九下-28.2 解直角三角形及其应用 第四课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-28.2 解直角三角形及其应用 第四课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览










文档简介
(共33张PPT)
28.2 解直角三角形及其应用
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
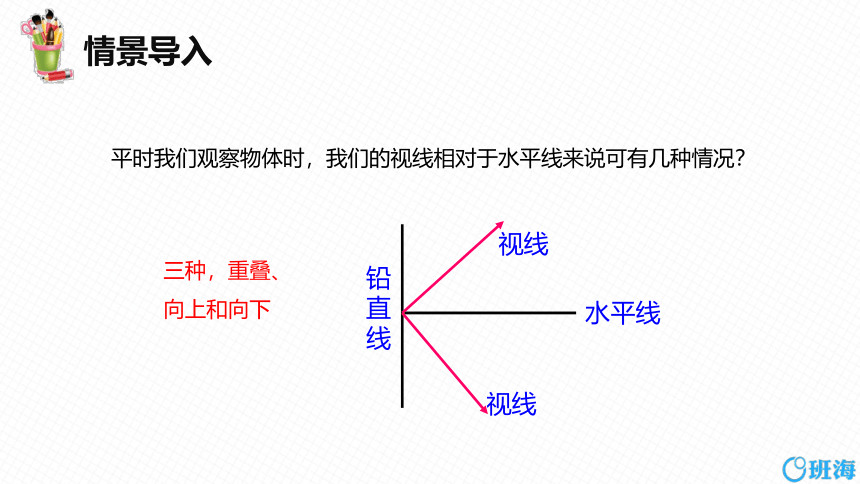
平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
三种,重叠、
向上和向下
铅直线
水平线
视线
视线
新课精讲
探索新知
1
知识点
仰角的应用
例1 2012年6月18日,“神舟”九号载人航天飞船与“天宫”
一号目标飞行器成功实现交会对接.“神舟”九号与“天宫”
一号的组合体在离地球表 面343 km的圆形轨道上运行,如图:
探索新知
当组合体运行到地球表面P 点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P 点的距离是多少(地球半径约为6 400 km, π 取3. 142,结果取整数)?
探索新知
分析:从组合体中能直接看到的地球表面最远点,是视线与地球相切时的切点. 如图,本例可以抽象为以地球中心为圆心、地球半径为半径的⊙O 的有关问题:其中点F 是组合体的位置,FQ 是⊙O 的切线,切点Q 是从组合体中观测地球时的最远点, 的长就是 地球表面上P,Q 两点间的距离.为计算 的长需先求出∠ POQ (即α)的度数.
探索新知
设∠ POQ= α,在图中,FQ 是⊙O 的切线,
△FOQ 是直角三角形.
∴α≈18.36°.
∴
解:
由此可知,当组合体在P 点正上方时,从中观测地球表面时的最远点距离P 点约2 051 km.
探索新知
总 结
利用解直角三角形解决实物模型问题的一般过程是:
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角
形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角
三角形,得到数学问题的答案,再转化得到实际问题的答案.
典题精讲
1 如图,建筑物BC 上有一旗杆AB,从与BC 相距40 m的D 处观测旗杆顶部A 的仰角为50°,观测旗杆底部B 的仰角为45°,求旗杆的高度(结果保留小数点后一位).
在Rt△BCD 中,DC=40,∠BDC=45°,
所以BC=40.
在Rt△ACD 中,tan∠ADC= ,
所以AC=DC · tan ∠ADC
=40×tan 50°≈47.67.
所以旗杆的高度为AB=AC-BC≈47.67-40≈7.7(m).
答:旗杆的高度约为7.7 m.
解:
典题精讲
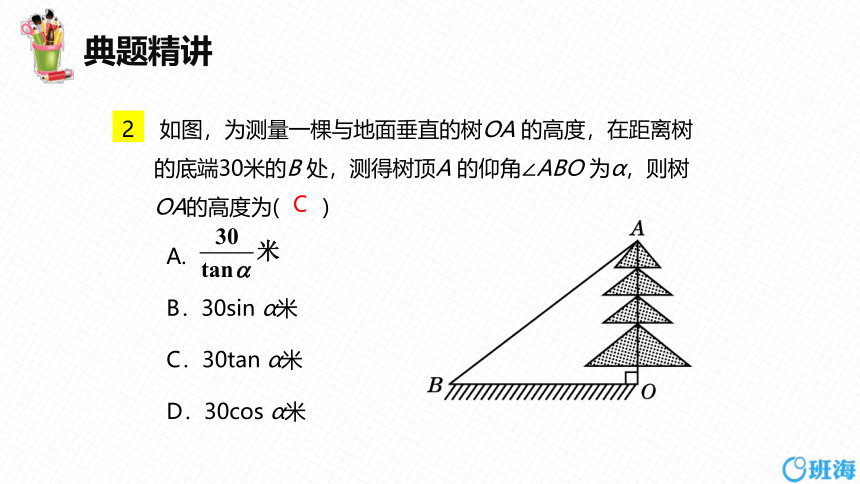
2 如图,为测量一棵与地面垂直的树OA 的高度,在距离树的底端30米的B 处,测得树顶A 的仰角∠ABO 为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米
C
典题精讲
3 湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB 底部50米的C 处,测得桥塔顶部A 的仰角为41.5°(如图).已知测量仪器CD 的高度为1米,则桥塔AB 的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米
C
探索新知
2
知识点
俯角的应用
例2 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,
看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,
这栋楼有多高(结果取整数)?
分析:我们知道,在视线与水平线所成的角中, 视线在水平线上方的是
仰角,视线在水平线下方的是俯角.因此,在图中, α =30°, β
=60°.在 Rt△ABD 中, α = 30°,AD = 120,所以可以利用解直
角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
探索新知
如图,α =30°, β =60°,AD=120.
∵
∴ BD =AD · tan α=120×tan30°
CD =AD · tan β=120×tan 60°
∴BC=BD+CD=
因此,这栋楼高约为277 m.
解:
探索新知
总 结
解决与俯角和仰角有关的实际问题,必须先根据视角(仰角、俯角)的意义画出水平线找准视角,建立数学模型,然后构造直角三角形,利用解直角三角形的知识解决要求的问题.
典题精讲
如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3 000 m的高空C处时,测得A 处渔政船的俯角为45°,测得B 处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB 是( )
A.3 000 m
B.3 000( +1)m
C.3 000( -1)m
D.1 500 m
1
C
典题精讲
如图,热气球的探测器显示,从热气球A 处看一栋楼顶部B 处的仰角为30°,看这栋楼底部C 处的俯角为60°,热气球A处与楼的水平距离为120 m,则这栋楼的高度为( )
A.160 m
B.120 m
C.300 m
D.160 m
2
A
典题精讲
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A 点处观测观光塔顶端C 处的仰角是60°,然后爬到该楼房顶端B 点处观测观光塔底部D
处的俯角是30°. 已知楼房高
AB 约是45 m,根据以上观测数
据可求观光塔的高CD 是
________m.
3
135
学以致用
小试牛刀
如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ≈1.414)( )
A.34.14米
B.34.1米
C.35.7米
D.35.74米
1
C
小试牛刀
聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O 是摩天轮的圆心,长为110米的AB 是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A 的仰角为33°,测得圆心O的仰角为21°,则小莹所在C 点到直径AB 所在的直线的距离约为(tan 33°≈0.65,tan 21°≈0.38)( )
A.169米
B.204米
C.240米
D.407米
2
B
小试牛刀
如图所示,一架水平飞行的无人机AB 的尾端点A测得正前方的桥的左端点P 的俯角为α,其中tan α=2 ,无人机的飞行高度AH为500 米,桥的长度为1 255米.
(1)求点H 到桥左端点P 的距离;
(2)若无人机前端点B 测得正前方的
桥的右端点Q 的俯角为30°,求
这架无人机的长度AB.
小试牛刀
解:
(1)在Rt△AHP 中,∵AH=500 ,tan∠APH=tan α
= ,∴HP=250(米).
答:点H 到桥左端点P 的距离为250米.
(2)如图,过点B 作BC⊥HQ 于点C.
在Rt△BCQ 中,∵BC=AH=500 ,
∠BQC=30°,∴CQ= =1 500.
∵PQ=1 255,∴CP=245.∵HP=250,
∴AB=HC=HP-CP=250-245=5(米).
答:这架无人机的长度AB 为5米.
小试牛刀
如图,某人为了测量小山顶上的塔ED 的高,他在山下
的点A 处测得塔尖点D 的仰角为45°,再沿AC 方向前进
60 m 到达山脚点B,测得塔尖点D 的仰角为60°,塔底
点E 的仰角为30°,求塔ED 的高度.(结果保留根号)
小试牛刀
由题知,∠DBC=60°,∠EBC=30°,∴∠DBE=∠DBC-∠EBC=60°-30°=30°.又∵∠BCD=90°,
∴∠BDC=90°-∠DBC=90°-60°=30°.
∴∠DBE=∠BDE.∴BE=DE.
设EC=x,则DE=BE=2EC=2x,DC=EC+DE=x+2x=3x,∴BC= .
由题知,∠DAC=45°,∠DCA=90°,AB=60,
∴△ACD 为等腰直角三角形.∴AC=DC.
∴x+60=3x,解得x=30+10 .
∴DE=2x=60+20 .
答:塔ED 的高为(60+20 )m.
解:
小试牛刀
金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB 的高,他们在旗杆正前方台阶上的点C 处,测得旗杆顶端A 的仰角为45°,朝着旗杆的方向走到台阶下的点F 处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE 为1米,点C 距地面的高度CD 为3米,台阶CF 的坡角为30°,且点E,F,D 在同一条直线上,求旗杆AB 的高度.(计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73)
小试牛刀
解:
如图所示,过点C 作CM⊥AB 于点M,则四边形MEDC 是矩形,∴ME=DC=3,CM=ED.
在Rt△AEF 中,∠AFE=60°,
设EF=x,则AF=2x,AE= x.
在Rt△FCD 中,CD=3,∠CFD=30°,
∴DF=3 .在Rt△AMC 中,∠ACM=45°,
∴MA=MC. ∵ED=MC,∴AM=ED.
∵AM=AE-ME,ED=EF+DF,∴ x-3=x+3 .
解得x=6+3 . ∴AE= ×(6+3 )=6 +9.
∴AB=AE-BE=9+6 -1≈18.4(米).
答:旗杆AB 的高度约为18.4米.
小试牛刀
如图,在办公楼AB 和实验楼CD 之间有一旗杆EF,从办公楼AB顶部A 点处经过旗杆顶部E 点恰好看到实验楼CD 的底部D 点,且俯角为45°,从实验楼CD 顶部C 点处经过旗杆顶部E 点恰好看到办公楼AB 的G 点,BG=1米,且俯角为30°,已知旗杆EF=9米,求办公楼AB 的高度.(结果精确到1米,参考数据: ≈1.41, ≈1.73)
小试牛刀
如图,过G 作CD 的垂线交CD 于P 交EF 于H,
由题意可知∠BAD=∠ADB=45°,
∴FD=EF=9米,AB=BD.
在Rt△GEH 中,
∵tan∠EGH
解得GH=8 米.∴BF=8 米.
∴PG=BD=BF+FD=(8 +9)米.
∴AB=(8 +9)米≈23米.
答:办公楼AB 的高度约为23米.
解:
课堂小结
课堂小结
解含有仰角、俯角问题的方法
(1)仰角和俯角是指视线相对于水平线而言的,不同位置的仰角
和俯角是不同的,可巧记为“上仰下俯”.在测量物体的高度
时,要善于将实际问题抽象为数学问题.
(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和
另一边,利用解直角三角形的知识就可以求出物体的高度.
(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实际问
题中的数量关系归结到直角三角形中来求解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.2 解直角三角形及其应用
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
三种,重叠、
向上和向下
铅直线
水平线
视线
视线
新课精讲
探索新知
1
知识点
仰角的应用
例1 2012年6月18日,“神舟”九号载人航天飞船与“天宫”
一号目标飞行器成功实现交会对接.“神舟”九号与“天宫”
一号的组合体在离地球表 面343 km的圆形轨道上运行,如图:
探索新知
当组合体运行到地球表面P 点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P 点的距离是多少(地球半径约为6 400 km, π 取3. 142,结果取整数)?
探索新知
分析:从组合体中能直接看到的地球表面最远点,是视线与地球相切时的切点. 如图,本例可以抽象为以地球中心为圆心、地球半径为半径的⊙O 的有关问题:其中点F 是组合体的位置,FQ 是⊙O 的切线,切点Q 是从组合体中观测地球时的最远点, 的长就是 地球表面上P,Q 两点间的距离.为计算 的长需先求出∠ POQ (即α)的度数.
探索新知
设∠ POQ= α,在图中,FQ 是⊙O 的切线,
△FOQ 是直角三角形.
∴α≈18.36°.
∴
解:
由此可知,当组合体在P 点正上方时,从中观测地球表面时的最远点距离P 点约2 051 km.
探索新知
总 结
利用解直角三角形解决实物模型问题的一般过程是:
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角
形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角
三角形,得到数学问题的答案,再转化得到实际问题的答案.
典题精讲
1 如图,建筑物BC 上有一旗杆AB,从与BC 相距40 m的D 处观测旗杆顶部A 的仰角为50°,观测旗杆底部B 的仰角为45°,求旗杆的高度(结果保留小数点后一位).
在Rt△BCD 中,DC=40,∠BDC=45°,
所以BC=40.
在Rt△ACD 中,tan∠ADC= ,
所以AC=DC · tan ∠ADC
=40×tan 50°≈47.67.
所以旗杆的高度为AB=AC-BC≈47.67-40≈7.7(m).
答:旗杆的高度约为7.7 m.
解:
典题精讲
2 如图,为测量一棵与地面垂直的树OA 的高度,在距离树的底端30米的B 处,测得树顶A 的仰角∠ABO 为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米
C
典题精讲
3 湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB 底部50米的C 处,测得桥塔顶部A 的仰角为41.5°(如图).已知测量仪器CD 的高度为1米,则桥塔AB 的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米
C
探索新知
2
知识点
俯角的应用
例2 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,
看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,
这栋楼有多高(结果取整数)?
分析:我们知道,在视线与水平线所成的角中, 视线在水平线上方的是
仰角,视线在水平线下方的是俯角.因此,在图中, α =30°, β
=60°.在 Rt△ABD 中, α = 30°,AD = 120,所以可以利用解直
角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
探索新知
如图,α =30°, β =60°,AD=120.
∵
∴ BD =AD · tan α=120×tan30°
CD =AD · tan β=120×tan 60°
∴BC=BD+CD=
因此,这栋楼高约为277 m.
解:
探索新知
总 结
解决与俯角和仰角有关的实际问题,必须先根据视角(仰角、俯角)的意义画出水平线找准视角,建立数学模型,然后构造直角三角形,利用解直角三角形的知识解决要求的问题.
典题精讲
如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3 000 m的高空C处时,测得A 处渔政船的俯角为45°,测得B 处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB 是( )
A.3 000 m
B.3 000( +1)m
C.3 000( -1)m
D.1 500 m
1
C
典题精讲
如图,热气球的探测器显示,从热气球A 处看一栋楼顶部B 处的仰角为30°,看这栋楼底部C 处的俯角为60°,热气球A处与楼的水平距离为120 m,则这栋楼的高度为( )
A.160 m
B.120 m
C.300 m
D.160 m
2
A
典题精讲
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A 点处观测观光塔顶端C 处的仰角是60°,然后爬到该楼房顶端B 点处观测观光塔底部D
处的俯角是30°. 已知楼房高
AB 约是45 m,根据以上观测数
据可求观光塔的高CD 是
________m.
3
135
学以致用
小试牛刀
如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ≈1.414)( )
A.34.14米
B.34.1米
C.35.7米
D.35.74米
1
C
小试牛刀
聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O 是摩天轮的圆心,长为110米的AB 是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A 的仰角为33°,测得圆心O的仰角为21°,则小莹所在C 点到直径AB 所在的直线的距离约为(tan 33°≈0.65,tan 21°≈0.38)( )
A.169米
B.204米
C.240米
D.407米
2
B
小试牛刀
如图所示,一架水平飞行的无人机AB 的尾端点A测得正前方的桥的左端点P 的俯角为α,其中tan α=2 ,无人机的飞行高度AH为500 米,桥的长度为1 255米.
(1)求点H 到桥左端点P 的距离;
(2)若无人机前端点B 测得正前方的
桥的右端点Q 的俯角为30°,求
这架无人机的长度AB.
小试牛刀
解:
(1)在Rt△AHP 中,∵AH=500 ,tan∠APH=tan α
= ,∴HP=250(米).
答:点H 到桥左端点P 的距离为250米.
(2)如图,过点B 作BC⊥HQ 于点C.
在Rt△BCQ 中,∵BC=AH=500 ,
∠BQC=30°,∴CQ= =1 500.
∵PQ=1 255,∴CP=245.∵HP=250,
∴AB=HC=HP-CP=250-245=5(米).
答:这架无人机的长度AB 为5米.
小试牛刀
如图,某人为了测量小山顶上的塔ED 的高,他在山下
的点A 处测得塔尖点D 的仰角为45°,再沿AC 方向前进
60 m 到达山脚点B,测得塔尖点D 的仰角为60°,塔底
点E 的仰角为30°,求塔ED 的高度.(结果保留根号)
小试牛刀
由题知,∠DBC=60°,∠EBC=30°,∴∠DBE=∠DBC-∠EBC=60°-30°=30°.又∵∠BCD=90°,
∴∠BDC=90°-∠DBC=90°-60°=30°.
∴∠DBE=∠BDE.∴BE=DE.
设EC=x,则DE=BE=2EC=2x,DC=EC+DE=x+2x=3x,∴BC= .
由题知,∠DAC=45°,∠DCA=90°,AB=60,
∴△ACD 为等腰直角三角形.∴AC=DC.
∴x+60=3x,解得x=30+10 .
∴DE=2x=60+20 .
答:塔ED 的高为(60+20 )m.
解:
小试牛刀
金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB 的高,他们在旗杆正前方台阶上的点C 处,测得旗杆顶端A 的仰角为45°,朝着旗杆的方向走到台阶下的点F 处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE 为1米,点C 距地面的高度CD 为3米,台阶CF 的坡角为30°,且点E,F,D 在同一条直线上,求旗杆AB 的高度.(计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73)
小试牛刀
解:
如图所示,过点C 作CM⊥AB 于点M,则四边形MEDC 是矩形,∴ME=DC=3,CM=ED.
在Rt△AEF 中,∠AFE=60°,
设EF=x,则AF=2x,AE= x.
在Rt△FCD 中,CD=3,∠CFD=30°,
∴DF=3 .在Rt△AMC 中,∠ACM=45°,
∴MA=MC. ∵ED=MC,∴AM=ED.
∵AM=AE-ME,ED=EF+DF,∴ x-3=x+3 .
解得x=6+3 . ∴AE= ×(6+3 )=6 +9.
∴AB=AE-BE=9+6 -1≈18.4(米).
答:旗杆AB 的高度约为18.4米.
小试牛刀
如图,在办公楼AB 和实验楼CD 之间有一旗杆EF,从办公楼AB顶部A 点处经过旗杆顶部E 点恰好看到实验楼CD 的底部D 点,且俯角为45°,从实验楼CD 顶部C 点处经过旗杆顶部E 点恰好看到办公楼AB 的G 点,BG=1米,且俯角为30°,已知旗杆EF=9米,求办公楼AB 的高度.(结果精确到1米,参考数据: ≈1.41, ≈1.73)
小试牛刀
如图,过G 作CD 的垂线交CD 于P 交EF 于H,
由题意可知∠BAD=∠ADB=45°,
∴FD=EF=9米,AB=BD.
在Rt△GEH 中,
∵tan∠EGH
解得GH=8 米.∴BF=8 米.
∴PG=BD=BF+FD=(8 +9)米.
∴AB=(8 +9)米≈23米.
答:办公楼AB 的高度约为23米.
解:
课堂小结
课堂小结
解含有仰角、俯角问题的方法
(1)仰角和俯角是指视线相对于水平线而言的,不同位置的仰角
和俯角是不同的,可巧记为“上仰下俯”.在测量物体的高度
时,要善于将实际问题抽象为数学问题.
(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和
另一边,利用解直角三角形的知识就可以求出物体的高度.
(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实际问
题中的数量关系归结到直角三角形中来求解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
