【班海精品】人教版(新)九下-28.1 锐角三角函数 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-28.1 锐角三角函数 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览









文档简介
(共45张PPT)
28.1 锐角三角函数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
A
B
C
BC=5.2m
AB=54.5m
θ
根据已知条件,你能用
塔身中心线与垂直中心
线所成的角度来描述比
萨斜塔的倾斜程度吗?
新课精讲
探索新知
1
知识点
正弦函数的定义
问 题
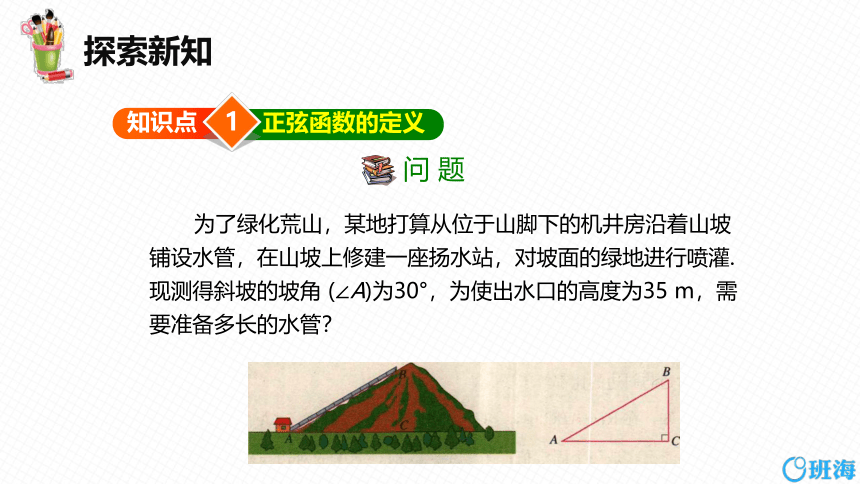
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡的坡角 (∠A)为30°,为使出水口的高度为35 m,需要准备多长的水管?
探索新知
这个问题可以归结为:在Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m, 求 AB (如图).
根据“在直角三角形中,30°角所对的边等于斜边的一半”,即
可得AB = 2BC = 70(m).也就是说,需要准备70 m长的水管.
探索新知
思考:
在上面的问题中,如果出水口的高度为50 m,那么需要准备多长的水管?
在上面求AB (所需水管的长度)的过程中,我们用到了结论:在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
探索新知
思考:
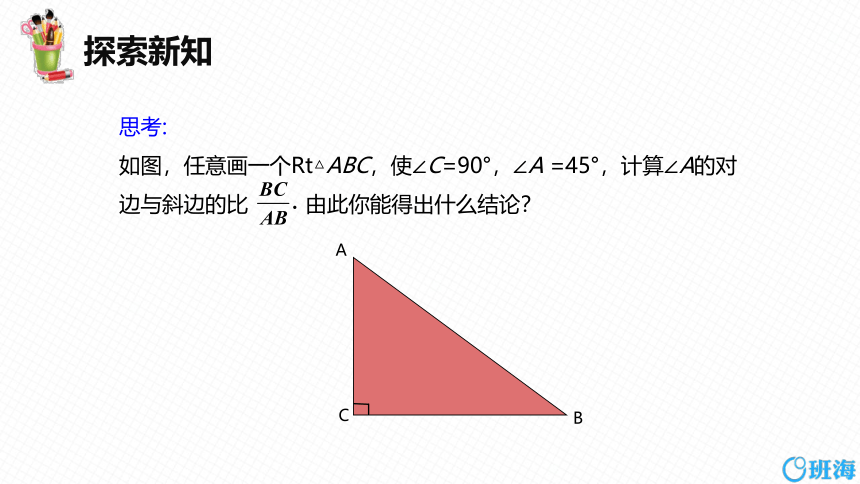
如图,任意画一个Rt△ABC,使∠C=90°,∠A =45°,计算∠A的对边与斜边的比 由此你能得出什么结论?
A
C
B
探索新知
如图,在Rt△ABC 中,∠C=90°,因为∠A= 45°,
所以Rt△ABC 是等腰直角三角形.由勾股定理得
AB 2 =AC 2+BC 2 = 2BC 2 ,
AB = BC.
因此
即在直角三角形中,当一个锐角等于45°时,无论这个直角三角形大小如何, 这个角的对边与斜边的比都等于
探索新知
综上可知,在Rt△ABC 中, ∠C = 90°,当∠A = 30°时, ∠A的对边与斜 边的比都等于 是一个固定值;当∠A = 45°时, ∠A的对边与斜边的比都等于 也是一个固定值.一般地,当∠A是任意一个确定的锐角时,它的对边与斜边的比是否也是一个固定值呢?
探索新知
探究:
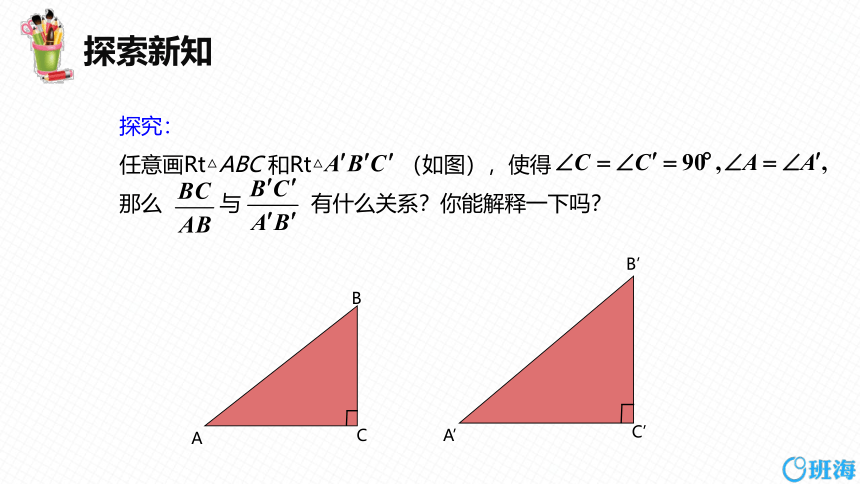
任意画Rt△ABC 和Rt△ (如图),使得 那么 与 有什么关系?你能解释一下吗?
A
C
B
A’
C’
B’
探索新知
在图中,由于 所以
Rt△ABC∽Rt△ 因此
即
这就是说,在Rt△ABC 中,当锐角A 的度数一定时,
无论这个直角三角形大小如何,∠A的对边与斜边的
比都是一个固定值.
探索新知
归 纳
如图,在Rt△ABC中,∠C=90°,我们把锐角A 的对边
与斜边的比叫做∠A 的正弦(sine),记作
sin A,即
例如,当∠A=30°时,我们有
sin A=sin 30°=
当∠A=45°时,我们有
sin A=sin 45°=
∠A的正弦sin A随着∠A的变化而变化.
探索新知
例1 如图 ,在 Rt△ABC 中,∠C = 90°,求 sin A
和 sin B 的值.
A
C
B
4
(1)
C
B
A
13
(2)
探索新知
解:如图(1),在Rt△ABC 中,由勾股定理得
因此
如图(2),在Rt△ABC 中,由勾股定理得
因此
探索新知
总 结
求sin A 就是要确定∠A 的对边与斜边 的比;求sin B 就是要确定∠B 的对边与斜边的比.
典题精讲
如图,在Rt△ABC 中,∠C=90°,
求sin A和sin B 的值.
解:由勾股定理得
所以
A
C
B
5
(1)
典题精讲
解:由勾股定理得
∴
A
C
B
1
(2)
典题精讲
在Rt△ABC 中,∠C=90°,AB=13,AC=5,则sin A 的值为( )
B.
C. D.
2
B
典题精讲
把Rt△ABC 三边的长度都扩大为原来的3倍,则锐角∠A
的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
A
典题精讲
在Rt△ABC中,∠C=90°,AC=12,BC=5,则sin A 的值为( )
A. B.
C. D.
4
D
A
C
B
探索新知
2
知识点
正弦函数的应用
例2 在Rt△ABC 中,∠C=90°,BC=2,sin A= 则边
AC 的长是( )
A. B.3 C. D.
解析:如图,
而BC=2,
A
探索新知
总 结
由正弦值求边长,当已知角的对边或斜边长时,通常先根据某个锐角的正弦的定义确定斜边或对边,再根据勾股定理求另一边;当已知角的邻边时,根据正弦函数的定义确定另外两边的比值,根据勾股定理列方程求解即可.
典题精讲
在Rt△ABC 中,∠C=90°,
∠A=90°,求sin A 的值.
解:如图.
∠B=90°-∠A=90°-60°=30°.
∴sin B=sin30°=
设AC=a,则AB=2a,
∴
典题精讲
2 在Rt△ABC 中,∠C=90°,AC=9,sin B= ,
则AB 的长等于( )
A.15 B.12 C.9 D.6
在Rt△ABC 中,∠C=90°,若AB=4,sin A= ,
则斜边上的高等于( )
A. B. C. D.
A
B
典题精讲
已知sin 6°=a,sin 36°=b,则sin2 6°=( )
A.a 2 B.2a
C.b 2 D.b
4
A
易错提醒
在直角三角形ABC 中,AC=4,BC=3,求sin A 的值.
解:
此题分两种情况:①当AC,BC 为两直角边时,AB=
=5,所以sin A= ;
②当BC 为直角边,AC 为斜边时,sin A= .
易错点:审题不清,找错直角边或斜边.
学以致用
小试牛刀
如图,在矩形ABCD 中,AB=8,BC =12,点E 是BC 的中点,连接AE,将△ABE 沿AE 折叠,点B 落在点F 处,连接FC,则sin∠ECF=( )
A.
B.
C.
D.
1
D
小试牛刀
如图,在平面直角坐标系中,点A 的坐标为(3,4),那么sin α 的值是( )
A.
B.
C.
D.
2
C
小试牛刀
如图,⊙O 的直径AB=4,BC 切⊙O 于点B,OC 平行于弦AD,OC=5,则AD 的长为( )
A.
B.
C.
D.
3
B
小试牛刀
4 已知:如图,在△ABC 中,∠C=90°,点D,E 分别
在边AB,AC上,DE∥BC,DE=3,BC=9.
(1)求 的值;
(2)若BD=10,求sin A 的值.
小试牛刀
解:
(1)∵DE∥BC,∴△ADE∽△ABC,∴
又∵DE=3,BC=9,∴
(2)根据(1)中 ,得
∵BD=10,DE=3,BC=9,
∴ ,解得AD=5,∴AB=15.
∴sin A=
小试牛刀
已知:如图,⊙O 的直径AB 为3,线段AC=4,直线
AC 和PM 分别与⊙O 相切于点A,M.
(1)求证:点P 是线段AC 的中点;
(2)求sin∠PMC 的值.
小试牛刀
(1)证明:如图,连接AM.∵AB是⊙O 的直径,
∴∠AMB=90°.∴∠AMC=90°.
∴∠MAC+∠C=90°,∠PMC+
∠PMA=90°.∵AC 和PM 分别与⊙O 相切于点A,
M,∴PM=PA. ∴∠PMA=∠PAM.
∴∠C= ∠PMC. ∴PC=PM.
∴PA=PC,即点P 是线段AC 的中点.
(2)解:∵AC 切⊙O 于点A,∴∠BAC=90°.又∵AB=3,
AC=4,∴BC=5.由(1)知∠C=∠PMC,
∴sin ∠PMC=sin C= .
小试牛刀
如图,在Rt△ABC中,∠ACB=90°,CD 是斜边AB 上的中
线,过点A作AE⊥CD,AE 分别与CD,CB 相交于点H,E,
AH=2CH.
(1)求sin B 的值;
(2)如果CD= ,求BE 的值.
小试牛刀
解:
(1)∵∠ACB=90°,CD 是斜边AB 上的中线,
∴CD=BD,∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,又∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,
∵AH=2CH,
∴由勾股定理得AC= CH,
∴CH∶AC=1∶ ,∴sinB= .
小试牛刀
(2)∵sinB= ,∴AC∶AB=1∶ ,
又CD= ,∴AB=2 ,∴AC=2,
∵sin∠CAH= ,
∴设CE=x (x>0),则AE= x,则x 2+2 2=( x )2,
∴CE=x=1,
在Rt△ABC 中,AC 2+BC 2=AB 2,
∴BC=4,∴BE=BC-CE=3.
小试牛刀
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于
第二、四象限内的A,B 两点,与x 轴交于点C,与y 轴交于点D,点B
的坐标是(m,-4),连接AO,AO=5,sin ∠AOC= .
(1)求反比例函数的解析式;
(2)连接OB,求△AOB 的面积.
小试牛刀
解:
(1)过点A作AE⊥x 轴于点E,如图所示.
设反比例函数的解析式为y= .
∵AE⊥x 轴,∴∠AEO=90°.
在Rt△AEO 中,AO=5,
sin ∠AOC= ,∠AEO=90°,
∴AE=AO · sin ∠AOC=3,OE= =4,
∴点A 的坐标为(-4,3).
∵点A (-4,3)在反比例函数的图象上,
∴3= ,解得k=-12.
∴反比例函数的解析式为y=- .
小试牛刀
(2)∵点B (m,-4)在反比例函数y=- 的图象上,
∴-4=- ,解得m=3,∴点B 的坐标为(3,-4).
设一次函数的解析式为y=ax+b,
将点A(-4,3),点B (3,-4)的坐标分别代入y=ax+b 中,
得 解得
∴一次函数的解析式为y=-x-1.
令一次函数y=-x-1中y=0,则0=-x-1,
解得x=-1,即点C 的坐标为(-1,0). ∴OC=1.
∴S△AOB= OC ·(yA-yB)= ×1×[3-(-4)]= .
课堂小结
课堂小结
锐角三角函数定义:
A
B
C
∠A的对边
┌
斜边
sin30° =
sin45°=
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.1 锐角三角函数
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
A
B
C
BC=5.2m
AB=54.5m
θ
根据已知条件,你能用
塔身中心线与垂直中心
线所成的角度来描述比
萨斜塔的倾斜程度吗?
新课精讲
探索新知
1
知识点
正弦函数的定义
问 题
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡的坡角 (∠A)为30°,为使出水口的高度为35 m,需要准备多长的水管?
探索新知
这个问题可以归结为:在Rt△ABC 中,∠C=90°,∠A=30°,BC = 35 m, 求 AB (如图).
根据“在直角三角形中,30°角所对的边等于斜边的一半”,即
可得AB = 2BC = 70(m).也就是说,需要准备70 m长的水管.
探索新知
思考:
在上面的问题中,如果出水口的高度为50 m,那么需要准备多长的水管?
在上面求AB (所需水管的长度)的过程中,我们用到了结论:在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
探索新知
思考:
如图,任意画一个Rt△ABC,使∠C=90°,∠A =45°,计算∠A的对边与斜边的比 由此你能得出什么结论?
A
C
B
探索新知
如图,在Rt△ABC 中,∠C=90°,因为∠A= 45°,
所以Rt△ABC 是等腰直角三角形.由勾股定理得
AB 2 =AC 2+BC 2 = 2BC 2 ,
AB = BC.
因此
即在直角三角形中,当一个锐角等于45°时,无论这个直角三角形大小如何, 这个角的对边与斜边的比都等于
探索新知
综上可知,在Rt△ABC 中, ∠C = 90°,当∠A = 30°时, ∠A的对边与斜 边的比都等于 是一个固定值;当∠A = 45°时, ∠A的对边与斜边的比都等于 也是一个固定值.一般地,当∠A是任意一个确定的锐角时,它的对边与斜边的比是否也是一个固定值呢?
探索新知
探究:
任意画Rt△ABC 和Rt△ (如图),使得 那么 与 有什么关系?你能解释一下吗?
A
C
B
A’
C’
B’
探索新知
在图中,由于 所以
Rt△ABC∽Rt△ 因此
即
这就是说,在Rt△ABC 中,当锐角A 的度数一定时,
无论这个直角三角形大小如何,∠A的对边与斜边的
比都是一个固定值.
探索新知
归 纳
如图,在Rt△ABC中,∠C=90°,我们把锐角A 的对边
与斜边的比叫做∠A 的正弦(sine),记作
sin A,即
例如,当∠A=30°时,我们有
sin A=sin 30°=
当∠A=45°时,我们有
sin A=sin 45°=
∠A的正弦sin A随着∠A的变化而变化.
探索新知
例1 如图 ,在 Rt△ABC 中,∠C = 90°,求 sin A
和 sin B 的值.
A
C
B
4
(1)
C
B
A
13
(2)
探索新知
解:如图(1),在Rt△ABC 中,由勾股定理得
因此
如图(2),在Rt△ABC 中,由勾股定理得
因此
探索新知
总 结
求sin A 就是要确定∠A 的对边与斜边 的比;求sin B 就是要确定∠B 的对边与斜边的比.
典题精讲
如图,在Rt△ABC 中,∠C=90°,
求sin A和sin B 的值.
解:由勾股定理得
所以
A
C
B
5
(1)
典题精讲
解:由勾股定理得
∴
A
C
B
1
(2)
典题精讲
在Rt△ABC 中,∠C=90°,AB=13,AC=5,则sin A 的值为( )
B.
C. D.
2
B
典题精讲
把Rt△ABC 三边的长度都扩大为原来的3倍,则锐角∠A
的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
A
典题精讲
在Rt△ABC中,∠C=90°,AC=12,BC=5,则sin A 的值为( )
A. B.
C. D.
4
D
A
C
B
探索新知
2
知识点
正弦函数的应用
例2 在Rt△ABC 中,∠C=90°,BC=2,sin A= 则边
AC 的长是( )
A. B.3 C. D.
解析:如图,
而BC=2,
A
探索新知
总 结
由正弦值求边长,当已知角的对边或斜边长时,通常先根据某个锐角的正弦的定义确定斜边或对边,再根据勾股定理求另一边;当已知角的邻边时,根据正弦函数的定义确定另外两边的比值,根据勾股定理列方程求解即可.
典题精讲
在Rt△ABC 中,∠C=90°,
∠A=90°,求sin A 的值.
解:如图.
∠B=90°-∠A=90°-60°=30°.
∴sin B=sin30°=
设AC=a,则AB=2a,
∴
典题精讲
2 在Rt△ABC 中,∠C=90°,AC=9,sin B= ,
则AB 的长等于( )
A.15 B.12 C.9 D.6
在Rt△ABC 中,∠C=90°,若AB=4,sin A= ,
则斜边上的高等于( )
A. B. C. D.
A
B
典题精讲
已知sin 6°=a,sin 36°=b,则sin2 6°=( )
A.a 2 B.2a
C.b 2 D.b
4
A
易错提醒
在直角三角形ABC 中,AC=4,BC=3,求sin A 的值.
解:
此题分两种情况:①当AC,BC 为两直角边时,AB=
=5,所以sin A= ;
②当BC 为直角边,AC 为斜边时,sin A= .
易错点:审题不清,找错直角边或斜边.
学以致用
小试牛刀
如图,在矩形ABCD 中,AB=8,BC =12,点E 是BC 的中点,连接AE,将△ABE 沿AE 折叠,点B 落在点F 处,连接FC,则sin∠ECF=( )
A.
B.
C.
D.
1
D
小试牛刀
如图,在平面直角坐标系中,点A 的坐标为(3,4),那么sin α 的值是( )
A.
B.
C.
D.
2
C
小试牛刀
如图,⊙O 的直径AB=4,BC 切⊙O 于点B,OC 平行于弦AD,OC=5,则AD 的长为( )
A.
B.
C.
D.
3
B
小试牛刀
4 已知:如图,在△ABC 中,∠C=90°,点D,E 分别
在边AB,AC上,DE∥BC,DE=3,BC=9.
(1)求 的值;
(2)若BD=10,求sin A 的值.
小试牛刀
解:
(1)∵DE∥BC,∴△ADE∽△ABC,∴
又∵DE=3,BC=9,∴
(2)根据(1)中 ,得
∵BD=10,DE=3,BC=9,
∴ ,解得AD=5,∴AB=15.
∴sin A=
小试牛刀
已知:如图,⊙O 的直径AB 为3,线段AC=4,直线
AC 和PM 分别与⊙O 相切于点A,M.
(1)求证:点P 是线段AC 的中点;
(2)求sin∠PMC 的值.
小试牛刀
(1)证明:如图,连接AM.∵AB是⊙O 的直径,
∴∠AMB=90°.∴∠AMC=90°.
∴∠MAC+∠C=90°,∠PMC+
∠PMA=90°.∵AC 和PM 分别与⊙O 相切于点A,
M,∴PM=PA. ∴∠PMA=∠PAM.
∴∠C= ∠PMC. ∴PC=PM.
∴PA=PC,即点P 是线段AC 的中点.
(2)解:∵AC 切⊙O 于点A,∴∠BAC=90°.又∵AB=3,
AC=4,∴BC=5.由(1)知∠C=∠PMC,
∴sin ∠PMC=sin C= .
小试牛刀
如图,在Rt△ABC中,∠ACB=90°,CD 是斜边AB 上的中
线,过点A作AE⊥CD,AE 分别与CD,CB 相交于点H,E,
AH=2CH.
(1)求sin B 的值;
(2)如果CD= ,求BE 的值.
小试牛刀
解:
(1)∵∠ACB=90°,CD 是斜边AB 上的中线,
∴CD=BD,∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,又∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,
∵AH=2CH,
∴由勾股定理得AC= CH,
∴CH∶AC=1∶ ,∴sinB= .
小试牛刀
(2)∵sinB= ,∴AC∶AB=1∶ ,
又CD= ,∴AB=2 ,∴AC=2,
∵sin∠CAH= ,
∴设CE=x (x>0),则AE= x,则x 2+2 2=( x )2,
∴CE=x=1,
在Rt△ABC 中,AC 2+BC 2=AB 2,
∴BC=4,∴BE=BC-CE=3.
小试牛刀
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于
第二、四象限内的A,B 两点,与x 轴交于点C,与y 轴交于点D,点B
的坐标是(m,-4),连接AO,AO=5,sin ∠AOC= .
(1)求反比例函数的解析式;
(2)连接OB,求△AOB 的面积.
小试牛刀
解:
(1)过点A作AE⊥x 轴于点E,如图所示.
设反比例函数的解析式为y= .
∵AE⊥x 轴,∴∠AEO=90°.
在Rt△AEO 中,AO=5,
sin ∠AOC= ,∠AEO=90°,
∴AE=AO · sin ∠AOC=3,OE= =4,
∴点A 的坐标为(-4,3).
∵点A (-4,3)在反比例函数的图象上,
∴3= ,解得k=-12.
∴反比例函数的解析式为y=- .
小试牛刀
(2)∵点B (m,-4)在反比例函数y=- 的图象上,
∴-4=- ,解得m=3,∴点B 的坐标为(3,-4).
设一次函数的解析式为y=ax+b,
将点A(-4,3),点B (3,-4)的坐标分别代入y=ax+b 中,
得 解得
∴一次函数的解析式为y=-x-1.
令一次函数y=-x-1中y=0,则0=-x-1,
解得x=-1,即点C 的坐标为(-1,0). ∴OC=1.
∴S△AOB= OC ·(yA-yB)= ×1×[3-(-4)]= .
课堂小结
课堂小结
锐角三角函数定义:
A
B
C
∠A的对边
┌
斜边
sin30° =
sin45°=
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
