【班海精品】人教版(新)九下-28.2 解直角三角形及其应用 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-28.2 解直角三角形及其应用 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览








文档简介
(共45张PPT)
28.2 解直角三角形及其应用
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
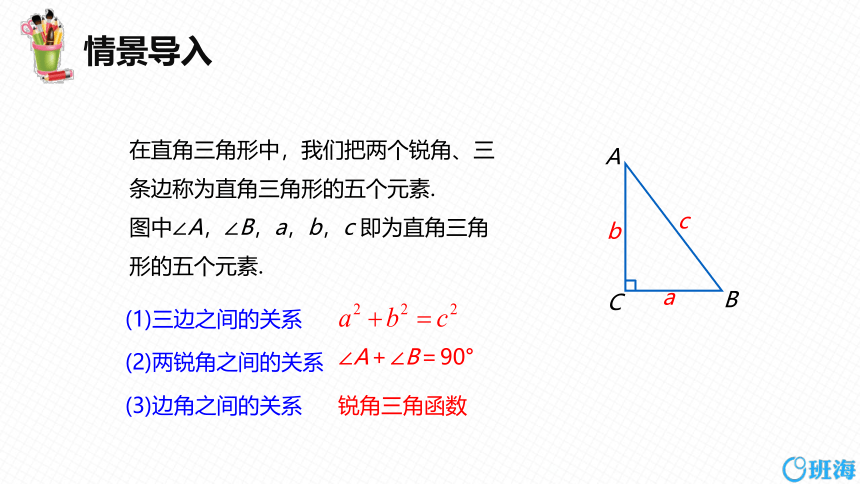
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c 即为直角三角形的五个元素.
锐角三角函数
新课精讲
探索新知
A
B
a
b
c
C
什么是解直角三角形
解直角三角形:
在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
探索新知
1
知识点
已知两边解直角三角形
探究:
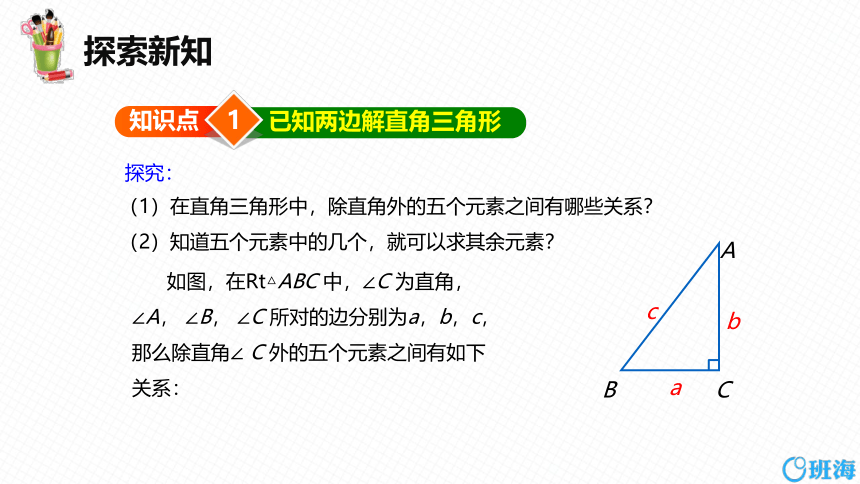
(1)在直角三角形中,除直角外的五个元素之间有哪些关系?
(2)知道五个元素中的几个,就可以求其余元素?
如图,在Rt△ABC 中,∠C 为直角,
∠A, ∠B, ∠C 所对的边分别为a,b,c,
那么除直角∠ C 外的五个元素之间有如下
关系:
A
B
a
b
c
C
探索新知
(1)三边之间的关系a 2+b 2=c 2 (勾股定理);
(2)两锐角之间的关系∠A+ ∠B = 90°;
(3)边角之间的关系
上述(3)中的A 都可以换成B,同时把a,b 互换.
探索新知
归 纳
利用这些关系,知道其中的两个元素(至少有一个是边),就可以求出其余三个未知元素.
探索新知
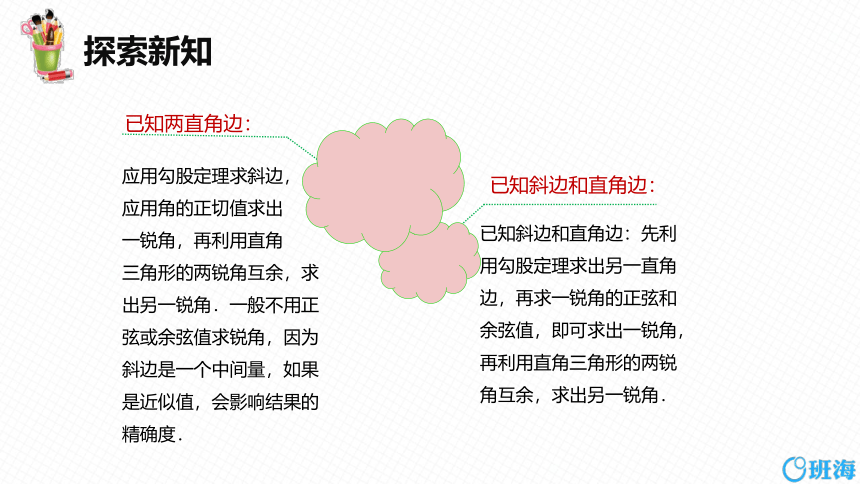
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
探索新知
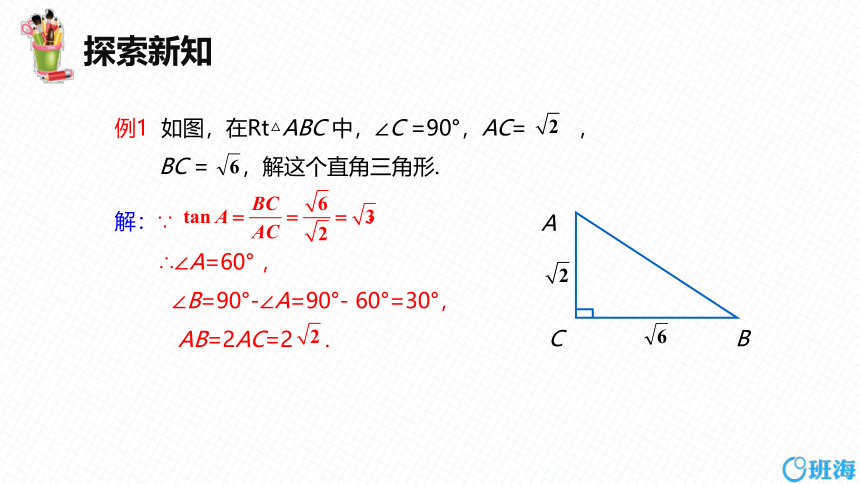
例1 如图,在Rt△ABC 中,∠C =90°,AC= ,BC = ,解这个直角三角形.
解:∵
∴∠A=60° ,
∠B=90°-∠A=90°- 60°=30°,
AB=2AC=2 .
A
B
C
探索新知
总 结
已知直角三角形的两边解直角三角形的方法:
先由勾股定理求第三边,再由两边中一直角边所对的角与这两边的关系,求出这个角,最后由两锐角互余求出第三个角.
典题精讲
1 在Rt△ABC 中,∠C =90°,根据下列条件解直角三角形:c =30,b =20;
解:∵c=30,b=20,
∴
∵tan A=
∴∠A≈48°.
∴∠B=90°-∠A≈90°-48°=42°.
典题精讲
在Rt△ABC 中,∠C=90°,AB=2 ,AC= ,
则∠A 的度数为( )
A.90° B.60° C.45° D.30°
2
D
在△ABC 中,∠C=90°,AB=4,AC=3,欲求∠A的值,
最适宜的做法是( )
A.计算tan A 的值求出
B.计算sin A 的值求出
C.计算cos A 的值求出
D.先根据sin B 求出∠B,再利用90°-∠B 求出
C
典题精讲
如图,在△ABC 中,∠B=90°,BC=2AB,则cos A=( )
A.
B.
C.
D.
4
D
探索新知
2
知识点
已知一边及一锐角解直角三角形
已知直角三角形的一边和一锐角,解直角三角形时,若已知一直角边a 和一锐角A: ① ∠B=90 °- ∠ A;
②c =
若已知斜边c 和一个锐角A: ① ∠ B=90°- ∠ A;
②a=c · sin A ; ③b=c · cos A.
探索新知
例2 如图,在Rt△ABC 中,∠C =90°,∠B = 35°,b =20,解这个直角三角形(结果保留小数点最后一位).
解:∠A=90°-∠B=90°- 35°=55°.
你还有其他方法求出c 吗?
探索新知
总 结
已知一锐角和一边解直角三角形的方法:
(1)在直角三角形中,若已知一个锐角和斜边,则可由两锐角
互余求出另一个锐角,然后利用三角函数(正弦、余弦)求
出两条直角边;
(2)若已知一个直角三角形的一个锐角和一条直角边,则可由
两锐角互余求出另一个锐角,然后利用余弦或正弦求出其
斜边,利用正切求出其另一条直角边.
典题精讲
1 在Rt△ABC 中,∠C=90°,根据下列条件解直角三角形:
(1) ∠B=72°,c =14;
(2) ∠B=30°,a = .
典题精讲
(1)由∠B=72°,c=14,
得∠A=90°-∠B=90°-72°=18°,
a=c · sin A=14×sin18°≈4.33,
b=c ·sin B=14×sin72°≈13.31.
(2)∵∠B=30°,a=
∴∠A=90°-∠B=90°-30°=60°,
b=
c=
解:
典题精讲
如图,在Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则BC 的长是( )
A. B.4
C.8 D.4
2
D
3 在△ABC 中,∠C=90°,若∠B=2∠A,b=3,则a 等于( )
A. B. C.6 D.
B
探索新知
3
知识点
已知一边及一锐角三角函数值解直角三角形
例3 如图,在△ABC 中,AB=1,AC= ,sin B = ,
求BC 的长.
导引:要求的BC 边不在直角三角形中,已知条件中有
∠B 的正弦值,作BC 边上的高,将∠B 置于直角
三角形中,利用解直角三角形就可解决问题.
探索新知
如图,过点A 作AD⊥BC 于点D.
∵AB=1,sin B=
∴AD=AB · sin B=
∴BD=
∴CD=
∴BC=CD+BD=
解:
探索新知
总 结
通过作垂线(高),将斜三角形分割成两个直角三角形,然后利用解直角三角形来解决边或角的问题,这种“化斜为直”的思想很常见.在作垂线时,要结合已知条件,充分利用已知条件,如本题若过B 点作AC 的垂线,则∠B 的正弦值就无法利用.
典题精讲
在Rt△ABC 中,∠C=90°,sin A= ,BC=6,
则AB=( )
A.4 B.6
C.8 D.10
D
典题精讲
2 如图是以△ABC 的边AB 为直径的半圆O,点C 恰好在半圆上,过点C 作CD⊥AB 于点D.已知cos∠ACD= ,BC=4,则AC 的长为( )
A.1
B.
C.3
D.
D
易错提醒
在△ABC 中,∠B=90°,BC=3,AB=5,求tanA,cosA的值.
解:
在Rt△ABC中,∠B=90°,
∴AC= .
∴tan A= ,cos A= .
易错总结:本题中已指出∠B=90°,所以AC 为斜边,而受习惯的影响,
常误以为∠C 的对边AB 是斜边.因此,解题时应认真审题,
注意所给条件,分清斜边和直角边,以防出错.
易错点:受思维定式影响误以为∠C 的对边为斜边造成错误.
学以致用
小试牛刀
如图,电线杆CD 的高度为h,两根拉线AC 与BC 相互垂直,∠CAB=α,则拉线BC 的长度为(A,D,B 在同一条直线上)( )
A.
B.
C.
D.h · cos α
1
B
小试牛刀
如图,在△ABC 中,AC⊥BC,∠ABC=30°,点D 是CB 延长线上的一点,且BD=BA,则tan∠DAC 的值为( )
A.2+
B.2
C.3+
D.3
2
A
小试牛刀
如图,四边形ABCD 是梯形,AD∥BC,CA 是∠BCD 的平分线,且AB⊥AC,AB=4,AD=6,则tan B=( )
A.
B.
C.
D.
3
B
小试牛刀
如图,已知在四边形ABCD 中,∠ABC =90°,∠ADC=90°,AB=6,CD=4,BC 的延长线与AD 的延长线交于点E.
(1)若∠A=60°,求BC 的长;
(2)若sin A= ,求AD 的长.
(注意:本题中的计算过程和结果均保留根号)
小试牛刀
解:
(1)∵∠A=60°,∠ABE=90°,AB=6,tan A= ,
∴∠E=30°,BE=6 · tan 60°=6 .
∵∠CDE=90°,CD=4,sin E= ,
∴CE= =8,
∴BC=BE-CE=6 -8.
小试牛刀
(2)∵∠ABE=90°,AB=6,sin A= ,
∴设BE=4x,则AE=5x,得AB=3x,
∴3x=6,得x=2,
∴BE=8,AE=10,
∴tan E= ,
解得DE= ,
∴AD=AE-DE=10- .
小试牛刀
如图,AD 是△ABC 的中线,tanB= ,cos C= ,AC= .求:
(1)BC 的长;
(2)sin∠ADC 的值.
小试牛刀
(1)如图,过点A作AE⊥BC 于点E,∵cos C= ,∴∠C
=45°.在Rt△ACE 中,CE=AC · cos C=1,∴AE=CE
=1.在Rt△ABE 中,tan B= ,即 = ,∴BE=
3AE=3,∴BC=BE+CE=4.
(2)∵AD 是△ABC 的中线,
∴CD= BC=2,∴DE=CD-CE=1.∵AE⊥BC,
DE=AE,∴∠ADC=45°,∴sin ∠ADC= .
解:
小试牛刀
如图,一座钢结构桥梁的框架是△ABC,水平横梁BC 长18米,中柱AD 高6米,其中D 是BC 的中点,且AD⊥BC.
(1)求sin B 的值;
(2)现需要加装支架DE,EF,其中点E 在AB上,BE=2AE,且
EF⊥BC,垂足为点F,求支架DE 的长.
小试牛刀
解:
(1)在Rt△ABD 中,∵BD=DC= BC=9米,AD=6米,
∴AB= (米).
∴sin B= .
(2)∵EF∥AD,∴△BEF∽△BAD,又∵BE=2AE,
∴EF=4米,BF=6米.∴DF=3米.
在Rt△DEF 中,DE= =5(米).
故支架DE 的长为5米.
小试牛刀
如图,PB 为⊙O 的切线,B 为切点,过B 作OP 的垂线BA,垂足为C,交⊙O于点A,连接PA,AO.并延长AO 交⊙O 于
点E,与PB 的延长线交于点D.
(1)求证:PA 是⊙O 的切线;
(2)若 ,且OC=4,求PA 的长和tan D 的值.
小试牛刀
(1)证明:如图,连接BO,
∵PB 为⊙O 的切线,B 为切点,
∴OB⊥PD,∠PBO=90°.
又∵OA=OB,OC⊥AB,
∴∠AOC=∠BOC.
又∵OP=OP,∴△PAO ≌ △PBO,
∴∠PAO=∠PBO=90°,
∴PA 是⊙O 的切线.
小试牛刀
(2)解:∵∠ACO=∠PAO=90°,∠AOC=∠POA,
∴△AOC∽△POA,∴ .
又∵OC=4,∴AC=6.
在Rt△AOC 中,
OA= ,
∴PA=OA=3,又易知PA=PB,∴PB=3.
在Rt△PAO 中,
PO= =13.
小试牛刀
如图,连接BE. ∵AE 为直径,∴∠ABE=90°.
又∵OC⊥AB,∴BE∥OP,
∴△DBE∽△DPO,BE=2OC=8.
∴ .
即 .解得BD .
∴在Rt△DBO 中,tan D= .
课堂小结
课堂小结
在直角三角形中有三条边、三个角,它们具备以下关系:
(1)三边之间关系:a 2+b 2=c 2 (勾股定理).
(2)锐角之间的关系:∠A+ ∠B = 90°.
(3)边角之间的关系:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
28.2 解直角三角形及其应用
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c 即为直角三角形的五个元素.
锐角三角函数
新课精讲
探索新知
A
B
a
b
c
C
什么是解直角三角形
解直角三角形:
在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
探索新知
1
知识点
已知两边解直角三角形
探究:
(1)在直角三角形中,除直角外的五个元素之间有哪些关系?
(2)知道五个元素中的几个,就可以求其余元素?
如图,在Rt△ABC 中,∠C 为直角,
∠A, ∠B, ∠C 所对的边分别为a,b,c,
那么除直角∠ C 外的五个元素之间有如下
关系:
A
B
a
b
c
C
探索新知
(1)三边之间的关系a 2+b 2=c 2 (勾股定理);
(2)两锐角之间的关系∠A+ ∠B = 90°;
(3)边角之间的关系
上述(3)中的A 都可以换成B,同时把a,b 互换.
探索新知
归 纳
利用这些关系,知道其中的两个元素(至少有一个是边),就可以求出其余三个未知元素.
探索新知
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
探索新知
例1 如图,在Rt△ABC 中,∠C =90°,AC= ,BC = ,解这个直角三角形.
解:∵
∴∠A=60° ,
∠B=90°-∠A=90°- 60°=30°,
AB=2AC=2 .
A
B
C
探索新知
总 结
已知直角三角形的两边解直角三角形的方法:
先由勾股定理求第三边,再由两边中一直角边所对的角与这两边的关系,求出这个角,最后由两锐角互余求出第三个角.
典题精讲
1 在Rt△ABC 中,∠C =90°,根据下列条件解直角三角形:c =30,b =20;
解:∵c=30,b=20,
∴
∵tan A=
∴∠A≈48°.
∴∠B=90°-∠A≈90°-48°=42°.
典题精讲
在Rt△ABC 中,∠C=90°,AB=2 ,AC= ,
则∠A 的度数为( )
A.90° B.60° C.45° D.30°
2
D
在△ABC 中,∠C=90°,AB=4,AC=3,欲求∠A的值,
最适宜的做法是( )
A.计算tan A 的值求出
B.计算sin A 的值求出
C.计算cos A 的值求出
D.先根据sin B 求出∠B,再利用90°-∠B 求出
C
典题精讲
如图,在△ABC 中,∠B=90°,BC=2AB,则cos A=( )
A.
B.
C.
D.
4
D
探索新知
2
知识点
已知一边及一锐角解直角三角形
已知直角三角形的一边和一锐角,解直角三角形时,若已知一直角边a 和一锐角A: ① ∠B=90 °- ∠ A;
②c =
若已知斜边c 和一个锐角A: ① ∠ B=90°- ∠ A;
②a=c · sin A ; ③b=c · cos A.
探索新知
例2 如图,在Rt△ABC 中,∠C =90°,∠B = 35°,b =20,解这个直角三角形(结果保留小数点最后一位).
解:∠A=90°-∠B=90°- 35°=55°.
你还有其他方法求出c 吗?
探索新知
总 结
已知一锐角和一边解直角三角形的方法:
(1)在直角三角形中,若已知一个锐角和斜边,则可由两锐角
互余求出另一个锐角,然后利用三角函数(正弦、余弦)求
出两条直角边;
(2)若已知一个直角三角形的一个锐角和一条直角边,则可由
两锐角互余求出另一个锐角,然后利用余弦或正弦求出其
斜边,利用正切求出其另一条直角边.
典题精讲
1 在Rt△ABC 中,∠C=90°,根据下列条件解直角三角形:
(1) ∠B=72°,c =14;
(2) ∠B=30°,a = .
典题精讲
(1)由∠B=72°,c=14,
得∠A=90°-∠B=90°-72°=18°,
a=c · sin A=14×sin18°≈4.33,
b=c ·sin B=14×sin72°≈13.31.
(2)∵∠B=30°,a=
∴∠A=90°-∠B=90°-30°=60°,
b=
c=
解:
典题精讲
如图,在Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则BC 的长是( )
A. B.4
C.8 D.4
2
D
3 在△ABC 中,∠C=90°,若∠B=2∠A,b=3,则a 等于( )
A. B. C.6 D.
B
探索新知
3
知识点
已知一边及一锐角三角函数值解直角三角形
例3 如图,在△ABC 中,AB=1,AC= ,sin B = ,
求BC 的长.
导引:要求的BC 边不在直角三角形中,已知条件中有
∠B 的正弦值,作BC 边上的高,将∠B 置于直角
三角形中,利用解直角三角形就可解决问题.
探索新知
如图,过点A 作AD⊥BC 于点D.
∵AB=1,sin B=
∴AD=AB · sin B=
∴BD=
∴CD=
∴BC=CD+BD=
解:
探索新知
总 结
通过作垂线(高),将斜三角形分割成两个直角三角形,然后利用解直角三角形来解决边或角的问题,这种“化斜为直”的思想很常见.在作垂线时,要结合已知条件,充分利用已知条件,如本题若过B 点作AC 的垂线,则∠B 的正弦值就无法利用.
典题精讲
在Rt△ABC 中,∠C=90°,sin A= ,BC=6,
则AB=( )
A.4 B.6
C.8 D.10
D
典题精讲
2 如图是以△ABC 的边AB 为直径的半圆O,点C 恰好在半圆上,过点C 作CD⊥AB 于点D.已知cos∠ACD= ,BC=4,则AC 的长为( )
A.1
B.
C.3
D.
D
易错提醒
在△ABC 中,∠B=90°,BC=3,AB=5,求tanA,cosA的值.
解:
在Rt△ABC中,∠B=90°,
∴AC= .
∴tan A= ,cos A= .
易错总结:本题中已指出∠B=90°,所以AC 为斜边,而受习惯的影响,
常误以为∠C 的对边AB 是斜边.因此,解题时应认真审题,
注意所给条件,分清斜边和直角边,以防出错.
易错点:受思维定式影响误以为∠C 的对边为斜边造成错误.
学以致用
小试牛刀
如图,电线杆CD 的高度为h,两根拉线AC 与BC 相互垂直,∠CAB=α,则拉线BC 的长度为(A,D,B 在同一条直线上)( )
A.
B.
C.
D.h · cos α
1
B
小试牛刀
如图,在△ABC 中,AC⊥BC,∠ABC=30°,点D 是CB 延长线上的一点,且BD=BA,则tan∠DAC 的值为( )
A.2+
B.2
C.3+
D.3
2
A
小试牛刀
如图,四边形ABCD 是梯形,AD∥BC,CA 是∠BCD 的平分线,且AB⊥AC,AB=4,AD=6,则tan B=( )
A.
B.
C.
D.
3
B
小试牛刀
如图,已知在四边形ABCD 中,∠ABC =90°,∠ADC=90°,AB=6,CD=4,BC 的延长线与AD 的延长线交于点E.
(1)若∠A=60°,求BC 的长;
(2)若sin A= ,求AD 的长.
(注意:本题中的计算过程和结果均保留根号)
小试牛刀
解:
(1)∵∠A=60°,∠ABE=90°,AB=6,tan A= ,
∴∠E=30°,BE=6 · tan 60°=6 .
∵∠CDE=90°,CD=4,sin E= ,
∴CE= =8,
∴BC=BE-CE=6 -8.
小试牛刀
(2)∵∠ABE=90°,AB=6,sin A= ,
∴设BE=4x,则AE=5x,得AB=3x,
∴3x=6,得x=2,
∴BE=8,AE=10,
∴tan E= ,
解得DE= ,
∴AD=AE-DE=10- .
小试牛刀
如图,AD 是△ABC 的中线,tanB= ,cos C= ,AC= .求:
(1)BC 的长;
(2)sin∠ADC 的值.
小试牛刀
(1)如图,过点A作AE⊥BC 于点E,∵cos C= ,∴∠C
=45°.在Rt△ACE 中,CE=AC · cos C=1,∴AE=CE
=1.在Rt△ABE 中,tan B= ,即 = ,∴BE=
3AE=3,∴BC=BE+CE=4.
(2)∵AD 是△ABC 的中线,
∴CD= BC=2,∴DE=CD-CE=1.∵AE⊥BC,
DE=AE,∴∠ADC=45°,∴sin ∠ADC= .
解:
小试牛刀
如图,一座钢结构桥梁的框架是△ABC,水平横梁BC 长18米,中柱AD 高6米,其中D 是BC 的中点,且AD⊥BC.
(1)求sin B 的值;
(2)现需要加装支架DE,EF,其中点E 在AB上,BE=2AE,且
EF⊥BC,垂足为点F,求支架DE 的长.
小试牛刀
解:
(1)在Rt△ABD 中,∵BD=DC= BC=9米,AD=6米,
∴AB= (米).
∴sin B= .
(2)∵EF∥AD,∴△BEF∽△BAD,又∵BE=2AE,
∴EF=4米,BF=6米.∴DF=3米.
在Rt△DEF 中,DE= =5(米).
故支架DE 的长为5米.
小试牛刀
如图,PB 为⊙O 的切线,B 为切点,过B 作OP 的垂线BA,垂足为C,交⊙O于点A,连接PA,AO.并延长AO 交⊙O 于
点E,与PB 的延长线交于点D.
(1)求证:PA 是⊙O 的切线;
(2)若 ,且OC=4,求PA 的长和tan D 的值.
小试牛刀
(1)证明:如图,连接BO,
∵PB 为⊙O 的切线,B 为切点,
∴OB⊥PD,∠PBO=90°.
又∵OA=OB,OC⊥AB,
∴∠AOC=∠BOC.
又∵OP=OP,∴△PAO ≌ △PBO,
∴∠PAO=∠PBO=90°,
∴PA 是⊙O 的切线.
小试牛刀
(2)解:∵∠ACO=∠PAO=90°,∠AOC=∠POA,
∴△AOC∽△POA,∴ .
又∵OC=4,∴AC=6.
在Rt△AOC 中,
OA= ,
∴PA=OA=3,又易知PA=PB,∴PB=3.
在Rt△PAO 中,
PO= =13.
小试牛刀
如图,连接BE. ∵AE 为直径,∴∠ABE=90°.
又∵OC⊥AB,∴BE∥OP,
∴△DBE∽△DPO,BE=2OC=8.
∴ .
即 .解得BD .
∴在Rt△DBO 中,tan D= .
课堂小结
课堂小结
在直角三角形中有三条边、三个角,它们具备以下关系:
(1)三边之间关系:a 2+b 2=c 2 (勾股定理).
(2)锐角之间的关系:∠A+ ∠B = 90°.
(3)边角之间的关系:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
