【班海精品】人教版(新)九下-29.2 三视图 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-29.2 三视图 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览








文档简介
(共37张PPT)
29.2 三 视 图
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
问题 请同学们认真观察如下正六棱柱 ,并画出其三视图,说出你画出的主视图中线段与正六棱柱中棱的对应关系,视图中线段的虚实情况.
新课精讲
探索新知
1
知识点
由三视图想象几何体
一个视图不能确定物体的空间形状,要根据三视
图描述几何体或实物原型时,必须将各视图对照起来
看. 根据主视图、俯视图和左视图想象立体图形的前后
面、上下面和左右面,然后再综合起来考虑整体图形.
探索新知
由三视图想象几何体:
(1)方法:由三视图想象立体图形时,要先分别根据主
视图、俯视图、左视图想象立体图形的前面、上面
和左侧面,然后再综合起来考虑整体图形.
(2)过程:由三视图想象几何体形状,可通过以下途径
进行分析.
探索新知
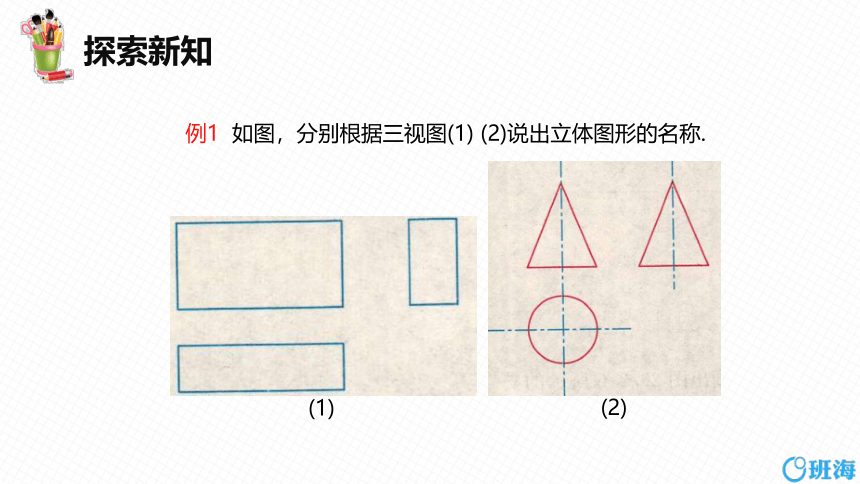
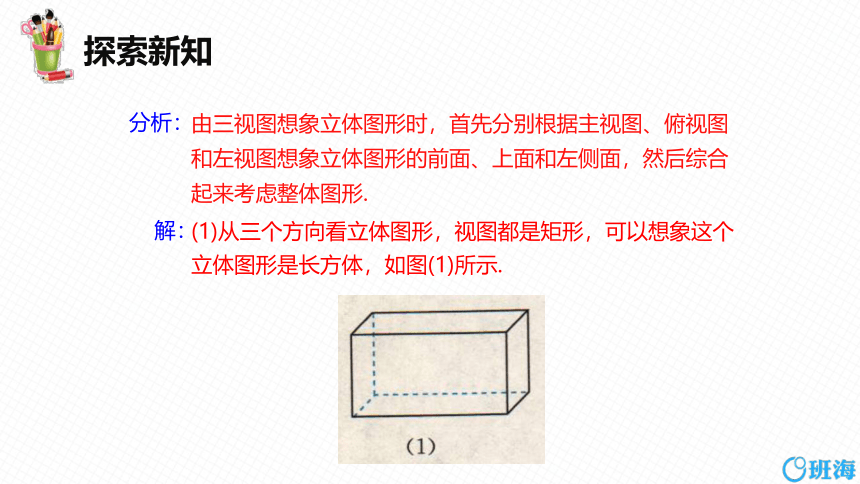
例1 如图,分别根据三视图(1) (2)说出立体图形的名称.
(1)
(2)
探索新知
由三视图想象立体图形时,首先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后综合起来考虑整体图形.
分析:
(1)从三个方向看立体图形,视图都是矩形,可以想象这个立体图形是长方体,如图(1)所示.
解:
探索新知
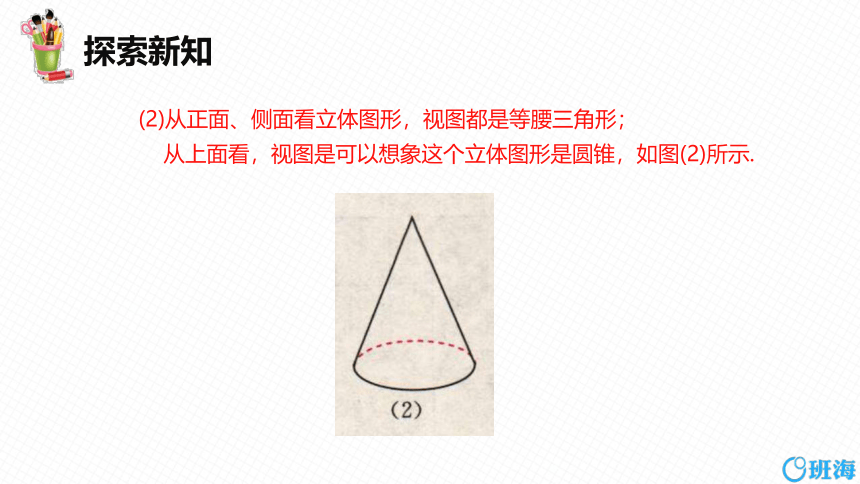
(2)从正面、侧面看立体图形,视图都是等腰三角形;
从上面看,视图是可以想象这个立体图形是圆锥,如图(2)所示.
探索新知
总 结
根据物体的三视图想象物体的形状,一般是由俯视图确定物体在平面上的形状,根据左视图、主视图想象出它在空间里的形状,从而确定物体的物状.
探索新知
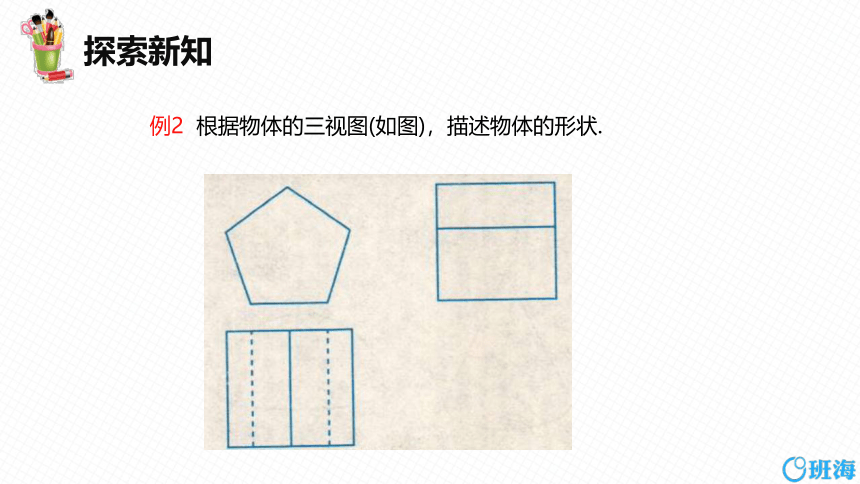
例2 根据物体的三视图(如图),描述物体的形状.
探索新知
由主视图可知,物体正面是正五边形; 由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到,另有两条棱(虚线表示)被遮挡;由左视图可知,物体左侧有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
分析:
探索新知
物体是正五棱柱形状的,如图所示.
解:
典题精讲
根据下列三视图,描述物体的形状.
1
(1)圆柱;(2)三棱柱(一条棱正对着观察者);
解:
典题精讲
(3)上面一个小圆柱,下面一个大圆柱组成的组合体;
(4)一个长方体右上角挖去一个四棱柱.
解:
典题精讲
如图是某个几何体的三视图,则该几何体是( )
A.圆锥
B.三棱柱
C.圆柱
D.三棱锥
2
B
典题精讲
如图中三视图对应的几何体是( )
3
C
典题精讲
如图是一个几何体的三视图,描述其结构特征,最准确的是( )
A.底面是正六边形
B.底面是六边形,侧面是等腰梯形的棱台
C.上、下底面是正六边形,侧面是等腰梯形的棱台
D.底面是正六边形,侧面是等腰三角形的棱锥
4
C
典题精讲
如图是一些完全相同的小正方体搭成的几何体的三视图,则这个几何体只能是( )
5
A
探索新知
2
知识点
由三视图确定组合体的数据
一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状是图中的( )
例3
D
探索新知
俯视图中,第一列最高有3个小立方块,第二列最高有2个小立方块,第三列最高有3个小立方块,因此,主视图从左到右可看到的小立方块个数依次为3、2、3,故选D.
导引:
探索新知
总 结
由一种视图猜想另一种视图,中间也是跳跃一步——还原几何体.先还原几何体,再确定另一种视图.
典题精讲
1
由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.3
B.4
C.5
D.6
C
典题精讲
2
一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11
B.12
C.13
D.14
B
学以致用
小试牛刀
一个几何体的三视图如图所示,该几何体是( )
D
1
小试牛刀
一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的最小值是( )
A. 6
B.7
C.9
D.10
B
2
小试牛刀
3
如图,根据主视图和俯视图找出物体(连线).
小试牛刀
4
如图是某物体的三种视图,请描述这个物体的形状,
并画出其图形.
直径和宽相等的圆柱和长方体的组合图形.
如图所示.
解:
小试牛刀
5
由一些大小相同的小正方体组成的简单几何体的主视
图和俯视图如图所示.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的个数为n,请你写
出n 的所有可能值.
小试牛刀
(1)由主视图可看出,此几何体有3列,从左往右第一
列1层,第二列2层,第三列3层,又由俯视图可知,
此几何体有2行,从前往后第一行3列,第二行2列,
则左视图的所有可能的结果有如图所示的5种情形
(画出一种即可):
(2)把以上五种情况下的几何体分别画出来,可得组成
几何体的小正方体的个数有8,9,10或11,即n=
8,9,10或11.
解:
小试牛刀
6
用小正方体搭一个几何体,使它的主视图和俯视图
如图所示.俯视图中小正方形中的字母表示在该位
置上小正方体的个数,请回答下列问题:
(1)a,b,c 各表示几?
(2)这个几何体最少由几个小正方体搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体的左视图.
小试牛刀
(1)a 为3,b 为1,c 为1.
(2)最少由9个小正方体搭成,最多由11个小正方体搭成.
(3)当d=e=1,f=2时,该几何体的左视图如图所示.
解:
课堂小结
课堂小结
1.通过这节课的学习,你有哪些收获?
2.由立体图形的三视图想象立体图形的形状时,你
有什么好的看法?与同伴交流一下.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.2 三 视 图
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
问题 请同学们认真观察如下正六棱柱 ,并画出其三视图,说出你画出的主视图中线段与正六棱柱中棱的对应关系,视图中线段的虚实情况.
新课精讲
探索新知
1
知识点
由三视图想象几何体
一个视图不能确定物体的空间形状,要根据三视
图描述几何体或实物原型时,必须将各视图对照起来
看. 根据主视图、俯视图和左视图想象立体图形的前后
面、上下面和左右面,然后再综合起来考虑整体图形.
探索新知
由三视图想象几何体:
(1)方法:由三视图想象立体图形时,要先分别根据主
视图、俯视图、左视图想象立体图形的前面、上面
和左侧面,然后再综合起来考虑整体图形.
(2)过程:由三视图想象几何体形状,可通过以下途径
进行分析.
探索新知
例1 如图,分别根据三视图(1) (2)说出立体图形的名称.
(1)
(2)
探索新知
由三视图想象立体图形时,首先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后综合起来考虑整体图形.
分析:
(1)从三个方向看立体图形,视图都是矩形,可以想象这个立体图形是长方体,如图(1)所示.
解:
探索新知
(2)从正面、侧面看立体图形,视图都是等腰三角形;
从上面看,视图是可以想象这个立体图形是圆锥,如图(2)所示.
探索新知
总 结
根据物体的三视图想象物体的形状,一般是由俯视图确定物体在平面上的形状,根据左视图、主视图想象出它在空间里的形状,从而确定物体的物状.
探索新知
例2 根据物体的三视图(如图),描述物体的形状.
探索新知
由主视图可知,物体正面是正五边形; 由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到,另有两条棱(虚线表示)被遮挡;由左视图可知,物体左侧有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
分析:
探索新知
物体是正五棱柱形状的,如图所示.
解:
典题精讲
根据下列三视图,描述物体的形状.
1
(1)圆柱;(2)三棱柱(一条棱正对着观察者);
解:
典题精讲
(3)上面一个小圆柱,下面一个大圆柱组成的组合体;
(4)一个长方体右上角挖去一个四棱柱.
解:
典题精讲
如图是某个几何体的三视图,则该几何体是( )
A.圆锥
B.三棱柱
C.圆柱
D.三棱锥
2
B
典题精讲
如图中三视图对应的几何体是( )
3
C
典题精讲
如图是一个几何体的三视图,描述其结构特征,最准确的是( )
A.底面是正六边形
B.底面是六边形,侧面是等腰梯形的棱台
C.上、下底面是正六边形,侧面是等腰梯形的棱台
D.底面是正六边形,侧面是等腰三角形的棱锥
4
C
典题精讲
如图是一些完全相同的小正方体搭成的几何体的三视图,则这个几何体只能是( )
5
A
探索新知
2
知识点
由三视图确定组合体的数据
一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状是图中的( )
例3
D
探索新知
俯视图中,第一列最高有3个小立方块,第二列最高有2个小立方块,第三列最高有3个小立方块,因此,主视图从左到右可看到的小立方块个数依次为3、2、3,故选D.
导引:
探索新知
总 结
由一种视图猜想另一种视图,中间也是跳跃一步——还原几何体.先还原几何体,再确定另一种视图.
典题精讲
1
由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.3
B.4
C.5
D.6
C
典题精讲
2
一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11
B.12
C.13
D.14
B
学以致用
小试牛刀
一个几何体的三视图如图所示,该几何体是( )
D
1
小试牛刀
一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的最小值是( )
A. 6
B.7
C.9
D.10
B
2
小试牛刀
3
如图,根据主视图和俯视图找出物体(连线).
小试牛刀
4
如图是某物体的三种视图,请描述这个物体的形状,
并画出其图形.
直径和宽相等的圆柱和长方体的组合图形.
如图所示.
解:
小试牛刀
5
由一些大小相同的小正方体组成的简单几何体的主视
图和俯视图如图所示.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的个数为n,请你写
出n 的所有可能值.
小试牛刀
(1)由主视图可看出,此几何体有3列,从左往右第一
列1层,第二列2层,第三列3层,又由俯视图可知,
此几何体有2行,从前往后第一行3列,第二行2列,
则左视图的所有可能的结果有如图所示的5种情形
(画出一种即可):
(2)把以上五种情况下的几何体分别画出来,可得组成
几何体的小正方体的个数有8,9,10或11,即n=
8,9,10或11.
解:
小试牛刀
6
用小正方体搭一个几何体,使它的主视图和俯视图
如图所示.俯视图中小正方形中的字母表示在该位
置上小正方体的个数,请回答下列问题:
(1)a,b,c 各表示几?
(2)这个几何体最少由几个小正方体搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体的左视图.
小试牛刀
(1)a 为3,b 为1,c 为1.
(2)最少由9个小正方体搭成,最多由11个小正方体搭成.
(3)当d=e=1,f=2时,该几何体的左视图如图所示.
解:
课堂小结
课堂小结
1.通过这节课的学习,你有哪些收获?
2.由立体图形的三视图想象立体图形的形状时,你
有什么好的看法?与同伴交流一下.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
