【班海精品】人教版(新)九下-29.1 投影 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-29.1 投影 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览









文档简介
(共43张PPT)
29.1 投 影
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
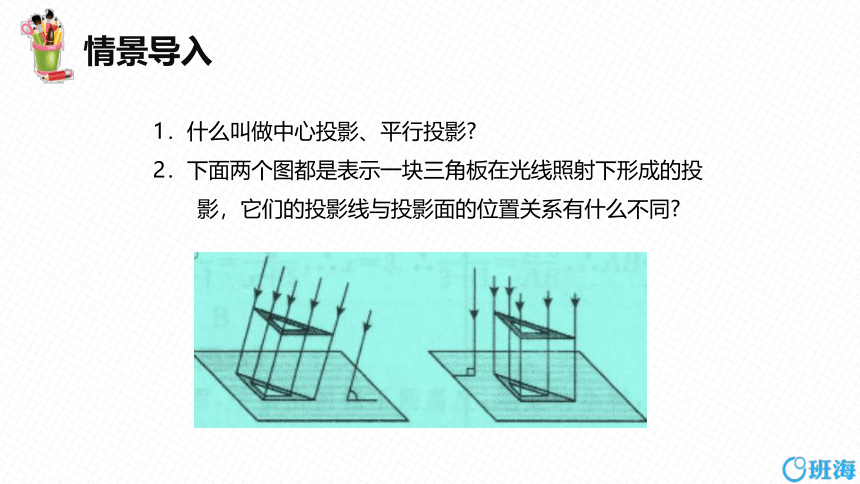
1.什么叫做中心投影、平行投影
2.下面两个图都是表示一块三角板在光线照射下形成的投
影,它们的投影线与投影面的位置关系有什么不同
新课精讲
探索新知
1
知识点
正投影的定义
正投影法:投影线与投影面垂直的平行投影法,
所得的投影,称为正投影 .
探索新知
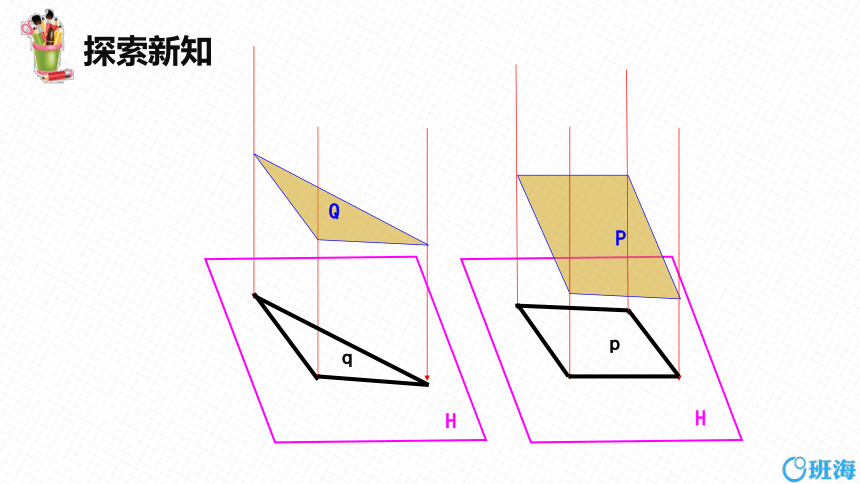
q
Q
H
P
H
p
探索新知
例1 如图所示的圆台的上下底面与投影线平行,圆台
的正投影是( )
A、矩形 B、两条线段
C、等腰梯形 D、圆环
根据正投影的定义及正投影形状分析.根据题意:
圆台的上下底面与投影线平行,则圆台的正投影是
该圆台的轴截面,即等腰梯形.故选C.
分析:
C
探索新知
总 结
物体的正投影的形状、大小与物体相对于投影面的位置有关.它分物体与投影面平行、倾斜、垂直三种情况.
典题精讲
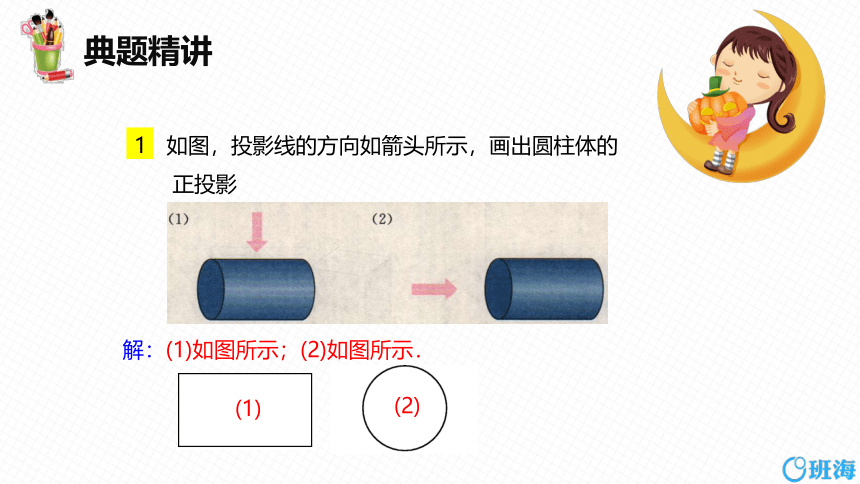
如图,投影线的方向如箭头所示,画出圆柱体的
正投影
解:(1)如图所示;(2)如图所示.
(1)
(2)
典题精讲
2 投影线________于投影面产生的投影叫做正投影;它包含以下两个要素:
(1)正投影是特殊的 ,它不可能是 .
(2)正投影只要求________与________垂直,与物体位
置无关.
垂直
平行投影
中心投影
光线
投影面
典题精讲
球的正投影是( )
A.圆 B.椭圆
C.点 D.圆环
正方形的正投影不可能是( )
A.线段 B.矩形
C.正方形 D.梯形
3
4
A
D
典题精讲
下列投影中,正投影有( )
A.0个 B.1个 C.2个 D.3个
5
B
典题精讲
6 如图,水杯的杯口与投影面平行,投影线的方向
如箭头所示,它的正投影是( )
D
典题精讲
底面与投影面垂直的圆锥体的正投影是( )
A.圆 B.三角形
C.矩形 D.正方形
7
B
把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( )
8
A
典题精讲
如图,投影线的方向如箭头所示,画出下列各图形的正投影.
9
解:如图所示.
探索新知
2
知识点
正投影的性质
如图,把一根直的细铁丝(记为线段AB )放在三个不同位置:
(1) 铁丝平行于投影面;
(2) 铁丝倾斜于投影面;
(3) 铁丝垂直于投影面(铁丝不一定要与投影面有交点).
三种情形下铁丝的正投影各是什么形状
探索新知
通过观察、测量可知:
(1)当线段AB 平行于投影面时,它的正投影是线段A1B1,
它们的大小关系为AB=A1B1 ;
(2)当线段AB 倾斜于投影面时,它的正投影是线段A2B2,
它们的大小关系为AB>A2B2 ;
(3)当线段AB 垂直于投影面时,它的正投影是一个点A3.
探索新知
如图,把一块正方形硬纸板P (记为正方形ABCD )放在
三个不同位置:
(1) 纸板平行于投影面; (2) 纸板倾斜于投影面;
(3) 纸板垂直于投影面.
三种情形下纸板的正投影各是什么形状
探索新知
通过观察、测量可知:
当纸板P 平行于投影面时,P 的正投影与P 的形状、大小一样;
当纸板P 倾斜于投影面时,P 的正投影与P 的形状、大小不完全 一样;
(3) 当纸板P 垂直于投影面时,P 的正投影成为一条线段.
探索新知
总 结
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、 大小完全相同.
探索新知
例2 画出如图摆放的正方体在投影面 上的正投影.
(1) 正方体的一个面ABCD 平行于投影面 (图(1));
(2) 正方体的一个面ABCD 倾斜于投影面, 底面ADEF 垂直于投
影面,并且其对角线AE 垂直于投影面(图(2) )
探索新知
(1)当正方体在如图 (1)的位置时,正方体的一个面ABCD 及与其相对的另一面与投影面平行,这两个面的正投影是与正方体的一个面的形状、大小完全相同的正方A′B′C′D′.正方形A′B′C′D′ 的四条边分别是正方体其余四个面(这些面垂直于投影面)的投影.因此,正方体的正投影是一个正方形.
分析:
探索新知
(2)当正方体在如图 (2)的位置时,它的面ABCD 和面ABGF 倾斜于投影面,它们的投影分别是矩形A′B′C′D′ 和A′B′G′F′ ;正方体其余两个侧面的投影也分别是上述矩形;上、下底面的投影分别是线段D′F′和C′G′.因此,正方体的投影是矩形F′G′C′D′ 其中线段A′B′ 把矩形一分为二.
探索新知
(1)如图 (1),正方体的正投影为正方形A′B′C′D′ ,
它与正方体的一个面是全等关系.
(2)如图(2),正方体的正投影为矩形F′G′C′D′ ,这个
矩形的长等于正方体的底面对角线长,矩形的宽
等于正方体的棱长.矩形上、下两边中点连线A′B′
是正方体的侧棱AB 及它所对的另一条侧棱EH 的
投影.
解:
探索新知
总 结
物体的正投影的形状、大小与物体相对于投影面
的位置有关.画一般立体图形的正投影的关键是找
出平行于投影面的立体图形的最大截面.
典题精讲
一根笔直的小木棒(记为线段AB ),它的正投影为线段CD,则下列各式中一定成立的是( )
A.AB=CD
B.AB≤CD
C.AB>CD
D.AB≥CD
1
D
典题精讲
2
小乐用一块矩形硬纸板在阳光下做投影实验,通过观察,发现这块矩形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形
B.线段
C.矩形
D.平行四边形
A
典题精讲
3
当棱长为20 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( )
A.200 cm2
B.300 cm2
C.400 cm2
D.600 cm2
C
易错提醒
如图所示,把正方体一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光垂直,则正方体在纸上的正投影是( )
易错点:对正方体的正投影的类型认识不全而致错.
C
学以致用
小试牛刀
几何体在平面P 的正投影,取决于( )
①几何体的形状;②投影面与几何体的位置关系;
③投影面P 的大小.
A.①② B.①③
C.②③ D.①②③
A
1
已知一根长为8 cm的木棒AB 与投影面平行,投影线垂直于投影面.
(1)求此时的影子A1B1的长度;
(2)如图是将木棒绕其端点A 逆时针旋转30°后的示意图(此时平面ABB2A2垂直于投影面),求旋转后木棒的影子A2B2的长
小试牛刀
2
分析:
(1)当木棒平行于投影面时,其正投影的长度与木棒的长度一致;(2)当木棒倾斜于投影面时,可转化为解直角三角形来求解.
小试牛刀
(1)因为木棒平行于投影面,
所以A1B1=AB=8 cm,
即此时的影子A1B1的长度为8 cm.
(2)过点A作AH⊥BB2于点H.
因为AA2⊥A2B2,BB2⊥A2B2,
所以四边形AA2B2H 为矩形,
所以AH=A2B2.
在Rt△ABH 中,∠BAH=30°,AB=8 cm,
所以A2B2=AH=AB·cos 30°=8× =4 (cm).
即旋转后木棒的影子A2B2的长为4 cm.
解:
小试牛刀
3
已知一纸板的形状为正方形ABCD,且边长为10 cm.如图,四边形A1B1C1D1是正方形ABCD 在面β 上的正投影,AD,BC 与投影面β 平行,且AB,CD 与投影面β 成30°角,求正方形ABCD 的正投影的面积.
小试牛刀
过点A作AH⊥BB1于点H.依题意,得∠BAH=30°,四边形A1B1C1D1是矩形,其中A1D1=AD,A1B1=AH.
∵AH⊥BB1,∠BAH=30°,
∴AH=AB·cos 30°=10× =5 (cm),
∴A1B1=AH=5 cm.∵A1D1=AD=10 cm,
∴S四边形A1B1C1D1=A1B1·A1D1=5 ×10=50 (cm2).
则正方形ABCD的正投影的面积是50 cm2.
规律总结:求投影的面积,先确定投影的形状,再根据相应的面积公
式,有针对性地求出相关线段的长.
解:
小试牛刀
4
一个圆锥的轴截面平行于投影面,圆锥的正投影是
等腰三角形,如图所示,等腰三角形的腰长为13 cm,
高为12 cm,求该圆锥的体积及表面积.
(提示:V圆锥= πr 2h,其中r 是底面圆的半径,h 是
圆锥的高)
小试牛刀
解:
由于圆锥的轴截面平行于投影面,其正投影是等腰三角形,因此圆锥的高等于等腰三角形的高;圆锥底面圆的半径等于等腰三角形底边长的一半.如图,作AD⊥BC 于D,AB=AC=13 cm,AD=12 cm,∴CD=5 cm,∴r=CD=5 cm,h=12 cm.
∴V圆锥= πr2h=100π cm3,
底面周长为l=2πr=10π cm,R=AC=13 cm,
S表= lR+πr2=90π cm2.
小试牛刀
5
操作与研究:
如图,△ABC 被平行光线照射,CD⊥AB 于D,AB 在
投影面上.
(1)指出图中AC 的投影是什么,CD 与BC 的投影呢?
(2)探究:当△ABC 为直角三角形(∠ACB=90°)时,
易得AC 2=AD ·AB,此时有如下结论:直角三角形
一直角边的平方等于它在斜边上的射影与斜边的乘
积,这一结论我们称为射影定理.
通过上述结论的推理,请证明
以下两个结论:
①BC 2=BD ·AB;②CD 2=AD ·BD.
小试牛刀
(1)解:AC 的投影是AD,CD 的投影是点D,BC 的投影是BD.
(2)证明:①易证得△BCD∽△BAC,
可得BC 2=BD ·AB;
②易证得△ACD∽△CBD,
可得CD 2=AD ·BD.
课堂小结
课堂小结
1.回顾正投影的含义及其性质;
2.反思作简单几何图形的正投影的过程及自己作图过
程中失误的原因,体会正投影的作图方法与技巧;
3.物体的正投影的形状、大小与它相对于投影面的位
置是否有关系?
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.1 投 影
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么叫做中心投影、平行投影
2.下面两个图都是表示一块三角板在光线照射下形成的投
影,它们的投影线与投影面的位置关系有什么不同
新课精讲
探索新知
1
知识点
正投影的定义
正投影法:投影线与投影面垂直的平行投影法,
所得的投影,称为正投影 .
探索新知
q
Q
H
P
H
p
探索新知
例1 如图所示的圆台的上下底面与投影线平行,圆台
的正投影是( )
A、矩形 B、两条线段
C、等腰梯形 D、圆环
根据正投影的定义及正投影形状分析.根据题意:
圆台的上下底面与投影线平行,则圆台的正投影是
该圆台的轴截面,即等腰梯形.故选C.
分析:
C
探索新知
总 结
物体的正投影的形状、大小与物体相对于投影面的位置有关.它分物体与投影面平行、倾斜、垂直三种情况.
典题精讲
如图,投影线的方向如箭头所示,画出圆柱体的
正投影
解:(1)如图所示;(2)如图所示.
(1)
(2)
典题精讲
2 投影线________于投影面产生的投影叫做正投影;它包含以下两个要素:
(1)正投影是特殊的 ,它不可能是 .
(2)正投影只要求________与________垂直,与物体位
置无关.
垂直
平行投影
中心投影
光线
投影面
典题精讲
球的正投影是( )
A.圆 B.椭圆
C.点 D.圆环
正方形的正投影不可能是( )
A.线段 B.矩形
C.正方形 D.梯形
3
4
A
D
典题精讲
下列投影中,正投影有( )
A.0个 B.1个 C.2个 D.3个
5
B
典题精讲
6 如图,水杯的杯口与投影面平行,投影线的方向
如箭头所示,它的正投影是( )
D
典题精讲
底面与投影面垂直的圆锥体的正投影是( )
A.圆 B.三角形
C.矩形 D.正方形
7
B
把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( )
8
A
典题精讲
如图,投影线的方向如箭头所示,画出下列各图形的正投影.
9
解:如图所示.
探索新知
2
知识点
正投影的性质
如图,把一根直的细铁丝(记为线段AB )放在三个不同位置:
(1) 铁丝平行于投影面;
(2) 铁丝倾斜于投影面;
(3) 铁丝垂直于投影面(铁丝不一定要与投影面有交点).
三种情形下铁丝的正投影各是什么形状
探索新知
通过观察、测量可知:
(1)当线段AB 平行于投影面时,它的正投影是线段A1B1,
它们的大小关系为AB=A1B1 ;
(2)当线段AB 倾斜于投影面时,它的正投影是线段A2B2,
它们的大小关系为AB>A2B2 ;
(3)当线段AB 垂直于投影面时,它的正投影是一个点A3.
探索新知
如图,把一块正方形硬纸板P (记为正方形ABCD )放在
三个不同位置:
(1) 纸板平行于投影面; (2) 纸板倾斜于投影面;
(3) 纸板垂直于投影面.
三种情形下纸板的正投影各是什么形状
探索新知
通过观察、测量可知:
当纸板P 平行于投影面时,P 的正投影与P 的形状、大小一样;
当纸板P 倾斜于投影面时,P 的正投影与P 的形状、大小不完全 一样;
(3) 当纸板P 垂直于投影面时,P 的正投影成为一条线段.
探索新知
总 结
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、 大小完全相同.
探索新知
例2 画出如图摆放的正方体在投影面 上的正投影.
(1) 正方体的一个面ABCD 平行于投影面 (图(1));
(2) 正方体的一个面ABCD 倾斜于投影面, 底面ADEF 垂直于投
影面,并且其对角线AE 垂直于投影面(图(2) )
探索新知
(1)当正方体在如图 (1)的位置时,正方体的一个面ABCD 及与其相对的另一面与投影面平行,这两个面的正投影是与正方体的一个面的形状、大小完全相同的正方A′B′C′D′.正方形A′B′C′D′ 的四条边分别是正方体其余四个面(这些面垂直于投影面)的投影.因此,正方体的正投影是一个正方形.
分析:
探索新知
(2)当正方体在如图 (2)的位置时,它的面ABCD 和面ABGF 倾斜于投影面,它们的投影分别是矩形A′B′C′D′ 和A′B′G′F′ ;正方体其余两个侧面的投影也分别是上述矩形;上、下底面的投影分别是线段D′F′和C′G′.因此,正方体的投影是矩形F′G′C′D′ 其中线段A′B′ 把矩形一分为二.
探索新知
(1)如图 (1),正方体的正投影为正方形A′B′C′D′ ,
它与正方体的一个面是全等关系.
(2)如图(2),正方体的正投影为矩形F′G′C′D′ ,这个
矩形的长等于正方体的底面对角线长,矩形的宽
等于正方体的棱长.矩形上、下两边中点连线A′B′
是正方体的侧棱AB 及它所对的另一条侧棱EH 的
投影.
解:
探索新知
总 结
物体的正投影的形状、大小与物体相对于投影面
的位置有关.画一般立体图形的正投影的关键是找
出平行于投影面的立体图形的最大截面.
典题精讲
一根笔直的小木棒(记为线段AB ),它的正投影为线段CD,则下列各式中一定成立的是( )
A.AB=CD
B.AB≤CD
C.AB>CD
D.AB≥CD
1
D
典题精讲
2
小乐用一块矩形硬纸板在阳光下做投影实验,通过观察,发现这块矩形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形
B.线段
C.矩形
D.平行四边形
A
典题精讲
3
当棱长为20 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( )
A.200 cm2
B.300 cm2
C.400 cm2
D.600 cm2
C
易错提醒
如图所示,把正方体一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光垂直,则正方体在纸上的正投影是( )
易错点:对正方体的正投影的类型认识不全而致错.
C
学以致用
小试牛刀
几何体在平面P 的正投影,取决于( )
①几何体的形状;②投影面与几何体的位置关系;
③投影面P 的大小.
A.①② B.①③
C.②③ D.①②③
A
1
已知一根长为8 cm的木棒AB 与投影面平行,投影线垂直于投影面.
(1)求此时的影子A1B1的长度;
(2)如图是将木棒绕其端点A 逆时针旋转30°后的示意图(此时平面ABB2A2垂直于投影面),求旋转后木棒的影子A2B2的长
小试牛刀
2
分析:
(1)当木棒平行于投影面时,其正投影的长度与木棒的长度一致;(2)当木棒倾斜于投影面时,可转化为解直角三角形来求解.
小试牛刀
(1)因为木棒平行于投影面,
所以A1B1=AB=8 cm,
即此时的影子A1B1的长度为8 cm.
(2)过点A作AH⊥BB2于点H.
因为AA2⊥A2B2,BB2⊥A2B2,
所以四边形AA2B2H 为矩形,
所以AH=A2B2.
在Rt△ABH 中,∠BAH=30°,AB=8 cm,
所以A2B2=AH=AB·cos 30°=8× =4 (cm).
即旋转后木棒的影子A2B2的长为4 cm.
解:
小试牛刀
3
已知一纸板的形状为正方形ABCD,且边长为10 cm.如图,四边形A1B1C1D1是正方形ABCD 在面β 上的正投影,AD,BC 与投影面β 平行,且AB,CD 与投影面β 成30°角,求正方形ABCD 的正投影的面积.
小试牛刀
过点A作AH⊥BB1于点H.依题意,得∠BAH=30°,四边形A1B1C1D1是矩形,其中A1D1=AD,A1B1=AH.
∵AH⊥BB1,∠BAH=30°,
∴AH=AB·cos 30°=10× =5 (cm),
∴A1B1=AH=5 cm.∵A1D1=AD=10 cm,
∴S四边形A1B1C1D1=A1B1·A1D1=5 ×10=50 (cm2).
则正方形ABCD的正投影的面积是50 cm2.
规律总结:求投影的面积,先确定投影的形状,再根据相应的面积公
式,有针对性地求出相关线段的长.
解:
小试牛刀
4
一个圆锥的轴截面平行于投影面,圆锥的正投影是
等腰三角形,如图所示,等腰三角形的腰长为13 cm,
高为12 cm,求该圆锥的体积及表面积.
(提示:V圆锥= πr 2h,其中r 是底面圆的半径,h 是
圆锥的高)
小试牛刀
解:
由于圆锥的轴截面平行于投影面,其正投影是等腰三角形,因此圆锥的高等于等腰三角形的高;圆锥底面圆的半径等于等腰三角形底边长的一半.如图,作AD⊥BC 于D,AB=AC=13 cm,AD=12 cm,∴CD=5 cm,∴r=CD=5 cm,h=12 cm.
∴V圆锥= πr2h=100π cm3,
底面周长为l=2πr=10π cm,R=AC=13 cm,
S表= lR+πr2=90π cm2.
小试牛刀
5
操作与研究:
如图,△ABC 被平行光线照射,CD⊥AB 于D,AB 在
投影面上.
(1)指出图中AC 的投影是什么,CD 与BC 的投影呢?
(2)探究:当△ABC 为直角三角形(∠ACB=90°)时,
易得AC 2=AD ·AB,此时有如下结论:直角三角形
一直角边的平方等于它在斜边上的射影与斜边的乘
积,这一结论我们称为射影定理.
通过上述结论的推理,请证明
以下两个结论:
①BC 2=BD ·AB;②CD 2=AD ·BD.
小试牛刀
(1)解:AC 的投影是AD,CD 的投影是点D,BC 的投影是BD.
(2)证明:①易证得△BCD∽△BAC,
可得BC 2=BD ·AB;
②易证得△ACD∽△CBD,
可得CD 2=AD ·BD.
课堂小结
课堂小结
1.回顾正投影的含义及其性质;
2.反思作简单几何图形的正投影的过程及自己作图过
程中失误的原因,体会正投影的作图方法与技巧;
3.物体的正投影的形状、大小与它相对于投影面的位
置是否有关系?
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
