【班海精品】人教版(新)九下-29.2 三视图 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-29.2 三视图 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览








文档简介
(共37张PPT)
29.2 三 视 图
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
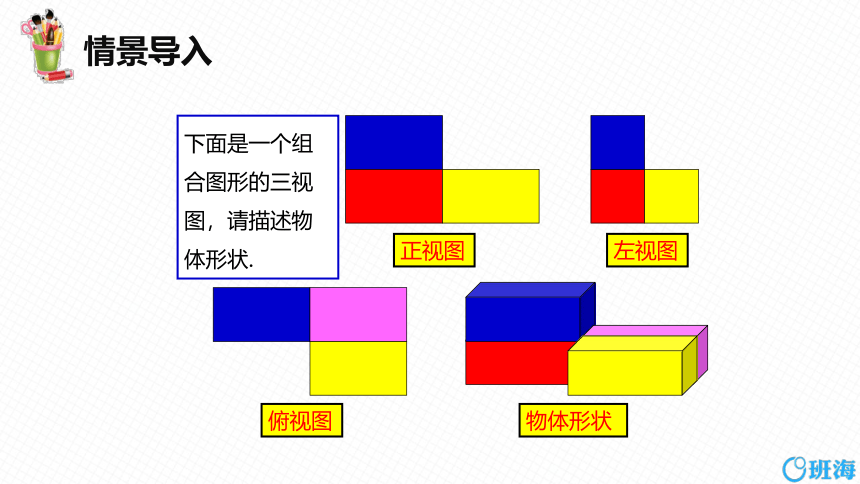
下面是一个组合图形的三视图,请描述物体形状.
正视图
左视图
俯视图
物体形状
新课精讲
探索新知
1
知识点
由三视图想象几何体的展开图
一个物体根据三视图描述几何体还原实物,然
后再由实物来想象该几何体的展开图.
探索新知
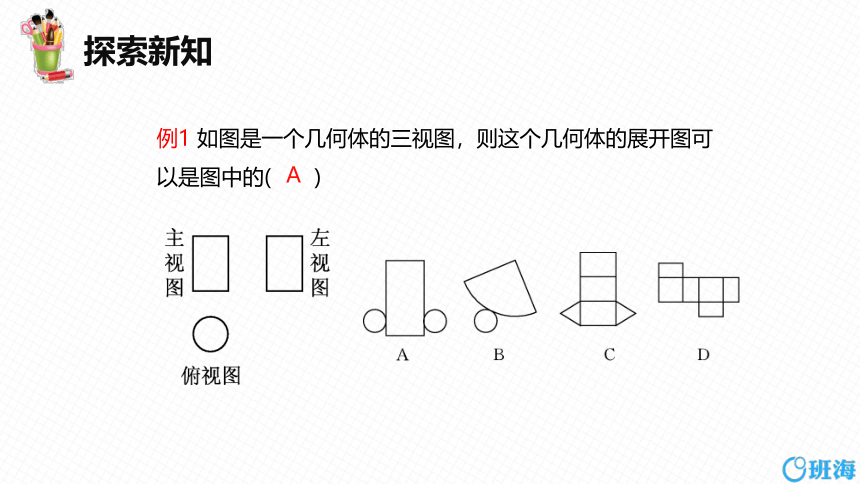
例1 如图是一个几何体的三视图,则这个几何体的展开图可以是图中的( )
A
探索新知
由三视图可知该几何体是圆柱,它的侧面展开图是矩形,两个底面的展开图是圆,故选择A.
导引:
探索新知
总 结
由三视图到平面展开图,其实就是中间跳跃一步,先由三视图到立体图形,再由立体图形到平面展开图.
典题精讲
1
(1)如图(1)所示.
(2)如图(2)所示.
解:
(1)
(2)
典题精讲
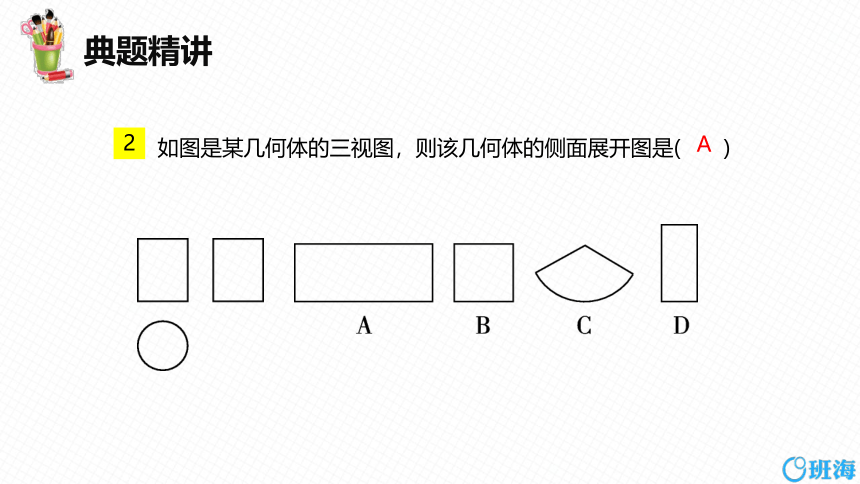
如图是某几何体的三视图,则该几何体的侧面展开图是( )
2
A
典题精讲
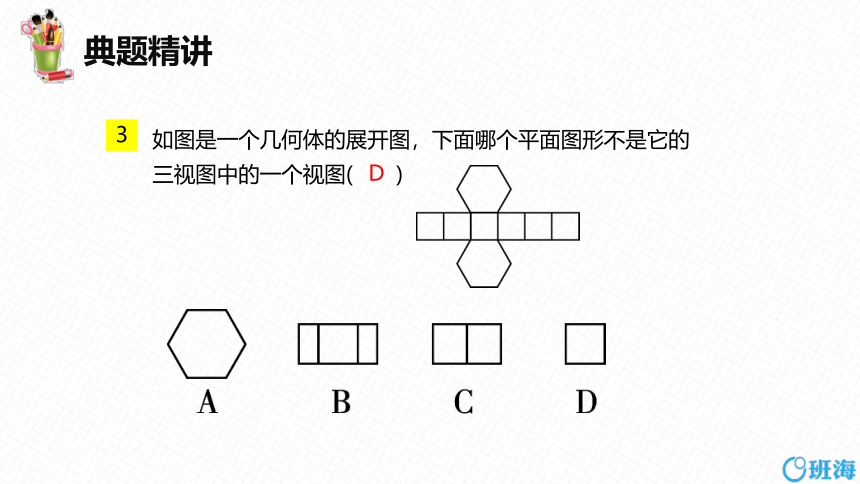
如图是一个几何体的展开图,下面哪个平面图形不是它的三视图中的一个视图( )
3
D
典题精讲
如图是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
A.90°
B.120°
C.135°
D.150°
4
B
探索新知
2
知识点
由三视图求几何体的面积和体积
例2 某工厂要加工一批密封罐,设计者给出了密封罐的
三视图(如图).请按照三视图确定制作每个密封罐所
需钢板的面积(图中尺寸单位:mm).
探索新知
对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图. 在实际生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,先由三视图想象出密封罐的形状,再进一步画出展开图,然后计算面积.
分析:
探索新知
由三视图可知,密封罐的形状是正六棱柱(如图1).
密封罐的高为50 mm,底面正六边形的直径为100
mm,边长为50 mm, 图2是它的展开图
解:
图1
图2
探索新知
由展开图可知,制作一个密封罐所需钢板的面积为
探索新知
总 结
由三视图求几何体的表面积或体积,必须先由三
视图还原出几何体,然后再确定几何体的表面积的组
成或体积的计算方式.最后利用公式去计算.
典题精讲
1
某工厂加工一批无底帐篷,设计者给出了帐篷的三视图请你按照三视图确定每顶帐篷的表面积(图中尺寸单位:cm).
S锥侧=π·150·240=36 000π(cm2),
S柱侧=2π·150·200=60 000π(cm2),
∴S表=S锥侧+S柱侧=36 000π+60 000π
=96 000π(cm2)=9.6π m2.
解:
典题精讲
2
由6个大小相同的正方体搭成的几何体如图所示,比较它的主视图,左视图和俯视图的面积,则( )
A.三个视图的面积一样大
B.主视图的面积最小
C.左视图的面积最小
D.俯视图的面积最小
C
典题精讲
3
如图,空心卷筒纸的高度为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1:4的三视图中,其主视图的面积是( )
cm2
B. cm2
C.30 cm2
D.7.5 cm2
D
典题精讲
4
如图是某工件的三视图,则此工件的表面积为( )
A.15π cm2
B.51π cm2
C.66π cm2
D.24π cm2
D
典题精讲
5
某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为( )
A.3π
B.2π
C.π
D.12
A
典题精讲
6
如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
A.800π+1 200
B.160π+1 700
C.3 200π+1 200
D.800π+3 000
D
学以致用
小试牛刀
如图是三个物体的三视图和展开图,请将同一物体的三视图和展开图搭配起来.
A 与________,
B 与________,
C 与________.
c
a
b
1
小试牛刀
如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
A.200 cm2
B.600 cm2
C.100π cm2
D.200π cm2
D
2
小试牛刀
3
如图为一几何体从不同方向看到的图形:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的长为10 cm,正三角形的边长
为4 cm,求这个几何体的侧面积.
(1)正三棱柱.
(2)如图(答案不唯一).
(3)10×4×3=120(cm2).
解:
小试牛刀
4
某直三棱柱零件如图①,张师傅根据此零件按1∶1的比
例画出准确的三视图如图②.已知在△EFG中,EF=
4 cm,∠EFG=45°,FG=12 cm,又知AD=8 cm.
(1)求AB 的长;
(2)求出这个直三棱柱的体积.
(1)过点E 作EH⊥FG 于
点H,则根据题意可得
出EH=AB,然后解直
角三角形即可得出答案.(2)根据三棱柱的体积
等于底面积乘棱柱的高进行计算即可.
思路导引:
小试牛刀
(1)过点E 作EH⊥FG 于点H,如图.
在Rt△EHF 中,EF=4 cm,∠EFH=45°,
∴EH=EF ·sin ∠EFH=4×sin 45°
=2 (cm).
由图形可知AB=EH=2 cm.
(2)直三棱柱的体积=S△EFG·AD= ×12×2×8
=96 (cm3).
解:
小试牛刀
5
已知一个模型的三视图如图所示(单位:m).
(1)请描述这个模型的形状.
(2)制作这个模型的木料密度为360 kg/m3,则这个模型的质量是多少千克?
(3)如果要给这个模型刷油漆,每千克油漆可以漆4 m2,需要油漆多少千克?
小试牛刀
(1)此模型由两个长方体组成:上面是一个小长方体,
下面是一个大长方体.
(2)模型的体积=5×6×10+2×3×1.5=309(m3),
则该模型的质量=309×360=111 240(kg).
(3)模型的表面积=2×3×2+2×1.5×2+10×5×2+
5×6×2+6×10×2=298(m2),
需要油漆298÷4=74.5(kg).
解:
小试牛刀
6
如图是一个几何体的三视图(单位:厘米):
(1)写出这个几何体的名称;
(2)根据所标数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表
面爬到AC 的中点D,请你求出最短线路的路程.
小试牛刀
(1)圆锥.
(2)表面积S=S扇形+S圆=πrl+πr2=12π+4π=
16π(平方厘米).
(3)如图,将圆锥侧面展开,线段BD 长为所求的最短路
程,由条件得∠BAB ′=120°,C 为弧BB ′的中点,
所以∠BAD=60°.连接BC,易知△ABC 为等边三角
形,又因为D 为AC 的中点,所以BD⊥
AC.从而可求得BD=3 厘米.
解:
课堂小结
课堂小结
对于由几何体的三种视图求它的表面积、体
积等相关数据的题目,首先由几何体的三种视图
想象出该几何体的形状,再利用三视图中的相关
数据确定立体图形的相关数据.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.2 三 视 图
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下面是一个组合图形的三视图,请描述物体形状.
正视图
左视图
俯视图
物体形状
新课精讲
探索新知
1
知识点
由三视图想象几何体的展开图
一个物体根据三视图描述几何体还原实物,然
后再由实物来想象该几何体的展开图.
探索新知
例1 如图是一个几何体的三视图,则这个几何体的展开图可以是图中的( )
A
探索新知
由三视图可知该几何体是圆柱,它的侧面展开图是矩形,两个底面的展开图是圆,故选择A.
导引:
探索新知
总 结
由三视图到平面展开图,其实就是中间跳跃一步,先由三视图到立体图形,再由立体图形到平面展开图.
典题精讲
1
(1)如图(1)所示.
(2)如图(2)所示.
解:
(1)
(2)
典题精讲
如图是某几何体的三视图,则该几何体的侧面展开图是( )
2
A
典题精讲
如图是一个几何体的展开图,下面哪个平面图形不是它的三视图中的一个视图( )
3
D
典题精讲
如图是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
A.90°
B.120°
C.135°
D.150°
4
B
探索新知
2
知识点
由三视图求几何体的面积和体积
例2 某工厂要加工一批密封罐,设计者给出了密封罐的
三视图(如图).请按照三视图确定制作每个密封罐所
需钢板的面积(图中尺寸单位:mm).
探索新知
对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图. 在实际生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,先由三视图想象出密封罐的形状,再进一步画出展开图,然后计算面积.
分析:
探索新知
由三视图可知,密封罐的形状是正六棱柱(如图1).
密封罐的高为50 mm,底面正六边形的直径为100
mm,边长为50 mm, 图2是它的展开图
解:
图1
图2
探索新知
由展开图可知,制作一个密封罐所需钢板的面积为
探索新知
总 结
由三视图求几何体的表面积或体积,必须先由三
视图还原出几何体,然后再确定几何体的表面积的组
成或体积的计算方式.最后利用公式去计算.
典题精讲
1
某工厂加工一批无底帐篷,设计者给出了帐篷的三视图请你按照三视图确定每顶帐篷的表面积(图中尺寸单位:cm).
S锥侧=π·150·240=36 000π(cm2),
S柱侧=2π·150·200=60 000π(cm2),
∴S表=S锥侧+S柱侧=36 000π+60 000π
=96 000π(cm2)=9.6π m2.
解:
典题精讲
2
由6个大小相同的正方体搭成的几何体如图所示,比较它的主视图,左视图和俯视图的面积,则( )
A.三个视图的面积一样大
B.主视图的面积最小
C.左视图的面积最小
D.俯视图的面积最小
C
典题精讲
3
如图,空心卷筒纸的高度为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1:4的三视图中,其主视图的面积是( )
cm2
B. cm2
C.30 cm2
D.7.5 cm2
D
典题精讲
4
如图是某工件的三视图,则此工件的表面积为( )
A.15π cm2
B.51π cm2
C.66π cm2
D.24π cm2
D
典题精讲
5
某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为( )
A.3π
B.2π
C.π
D.12
A
典题精讲
6
如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
A.800π+1 200
B.160π+1 700
C.3 200π+1 200
D.800π+3 000
D
学以致用
小试牛刀
如图是三个物体的三视图和展开图,请将同一物体的三视图和展开图搭配起来.
A 与________,
B 与________,
C 与________.
c
a
b
1
小试牛刀
如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
A.200 cm2
B.600 cm2
C.100π cm2
D.200π cm2
D
2
小试牛刀
3
如图为一几何体从不同方向看到的图形:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的长为10 cm,正三角形的边长
为4 cm,求这个几何体的侧面积.
(1)正三棱柱.
(2)如图(答案不唯一).
(3)10×4×3=120(cm2).
解:
小试牛刀
4
某直三棱柱零件如图①,张师傅根据此零件按1∶1的比
例画出准确的三视图如图②.已知在△EFG中,EF=
4 cm,∠EFG=45°,FG=12 cm,又知AD=8 cm.
(1)求AB 的长;
(2)求出这个直三棱柱的体积.
(1)过点E 作EH⊥FG 于
点H,则根据题意可得
出EH=AB,然后解直
角三角形即可得出答案.(2)根据三棱柱的体积
等于底面积乘棱柱的高进行计算即可.
思路导引:
小试牛刀
(1)过点E 作EH⊥FG 于点H,如图.
在Rt△EHF 中,EF=4 cm,∠EFH=45°,
∴EH=EF ·sin ∠EFH=4×sin 45°
=2 (cm).
由图形可知AB=EH=2 cm.
(2)直三棱柱的体积=S△EFG·AD= ×12×2×8
=96 (cm3).
解:
小试牛刀
5
已知一个模型的三视图如图所示(单位:m).
(1)请描述这个模型的形状.
(2)制作这个模型的木料密度为360 kg/m3,则这个模型的质量是多少千克?
(3)如果要给这个模型刷油漆,每千克油漆可以漆4 m2,需要油漆多少千克?
小试牛刀
(1)此模型由两个长方体组成:上面是一个小长方体,
下面是一个大长方体.
(2)模型的体积=5×6×10+2×3×1.5=309(m3),
则该模型的质量=309×360=111 240(kg).
(3)模型的表面积=2×3×2+2×1.5×2+10×5×2+
5×6×2+6×10×2=298(m2),
需要油漆298÷4=74.5(kg).
解:
小试牛刀
6
如图是一个几何体的三视图(单位:厘米):
(1)写出这个几何体的名称;
(2)根据所标数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表
面爬到AC 的中点D,请你求出最短线路的路程.
小试牛刀
(1)圆锥.
(2)表面积S=S扇形+S圆=πrl+πr2=12π+4π=
16π(平方厘米).
(3)如图,将圆锥侧面展开,线段BD 长为所求的最短路
程,由条件得∠BAB ′=120°,C 为弧BB ′的中点,
所以∠BAD=60°.连接BC,易知△ABC 为等边三角
形,又因为D 为AC 的中点,所以BD⊥
AC.从而可求得BD=3 厘米.
解:
课堂小结
课堂小结
对于由几何体的三种视图求它的表面积、体
积等相关数据的题目,首先由几何体的三种视图
想象出该几何体的形状,再利用三视图中的相关
数据确定立体图形的相关数据.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
