【班海精品】人教版(新)九下-29.2 三视图 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-29.2 三视图 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览









文档简介
(共43张PPT)
29.2 三 视 图
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
这首诗教会了我们怎样观察物体(横看、侧看、
近看、身处其中看),这类似于本节课所研究的内
容——三视图.
新课精讲
探索新知
1
知识点
几何体的三视图
当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图(view). 视图可以看作物体在某一方向光线下的正投影.对于同一个物体, 如果从不同方向观察,所得到的视图可能不同.如图是同一本书的三个不同的视图.
探索新知
我们知道,单一的视图通常只能反映物体一个方
面的形状.为了全面地反映物体的形状,生产实践中往
往采用多个视图来反映同一物体不同方面的形状.例如
图中右侧的三个视图,可以多方面反映飞机的形状.
探索新知
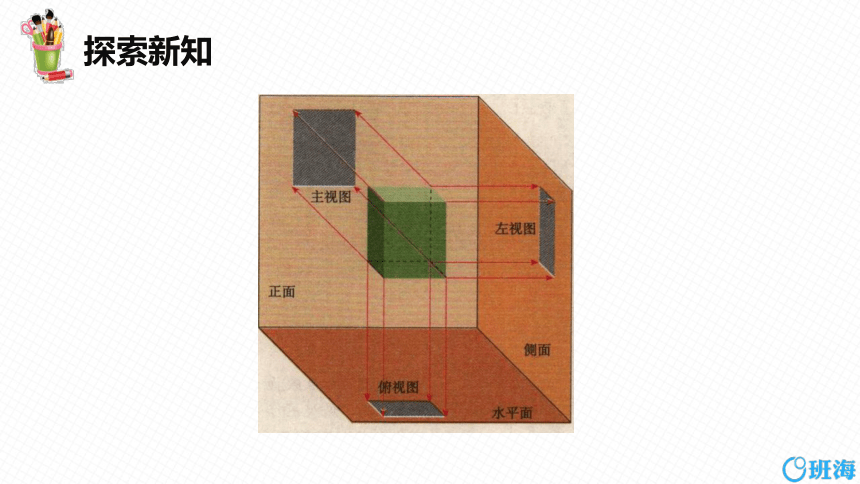
如下图,我们用三个互相垂直的平面(例如墙角处的三面墙壁) 作为投影面,其中正对着我们的平面叫做正面,下方的平面叫做水平面,右边的平面叫做侧面.对一个物体(例如一个长方体) 在三个投影面内进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图; 在侧面内得到的由左向右观察物体的视图,叫做左视图.
探索新知
探索新知
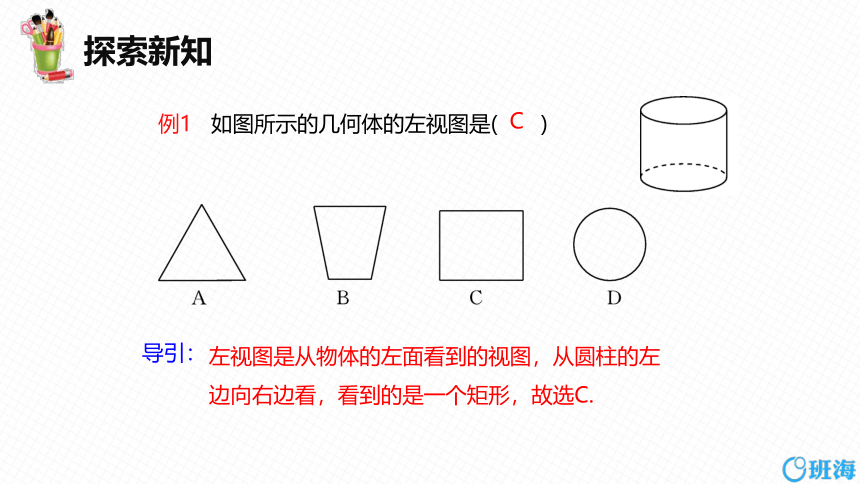
例1 如图所示的几何体的左视图是( )
左视图是从物体的左面看到的视图,从圆柱的左
边向右边看,看到的是一个矩形,故选C.
导引:
C
探索新知
总 结
单个几何体的三视图直接根据常见的几何体三视图中识别.
典题精讲
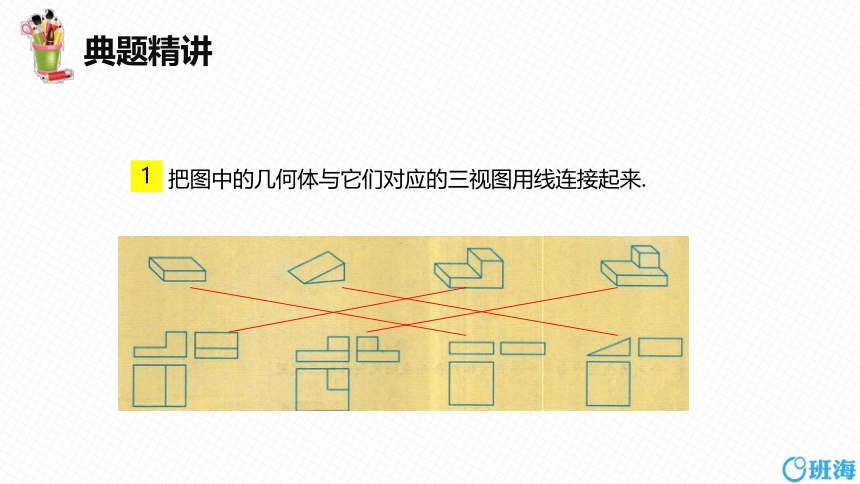
把图中的几何体与它们对应的三视图用线连接起来.
1
典题精讲
如图是由四个相同的小正方体组成的几何体,则它的主视图为( )
2
A
典题精讲
如图是一个空心圆柱体,它的左视图是( )
3
B
典题精讲
如图是一个水平放置的圆柱形物体,中间有一个细棒,则此几何体的俯视图是( )
4
C
典题精讲
下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
5
C
典题精讲
如图所示的几何体为圆台,其俯视图正确的是( )
6
C
典题精讲
下面几个几何体中,其主视图不是中心对称图形的是( )
7
C
探索新知
2
知识点
画几何体的三视图
如图(2),将三个投影面展开在一个平面内,得到这一物体的一张三视图(由主视图、俯视图和左视图组成).三视图中的各视图,分别从不 同方面表示物体的形状,三者合起来能够较全面地反映物体的形状.
探索新知
主视图
左视图
俯视图
长
宽
高
长
高
宽
高
长
宽
长对正,主视俯视长相等且对正
高平齐,俯视左视宽相等且对应
探索新知
例2 画出图中基本几何体的三视图
探索新知
画这些基本几何体的三视图时,要注意从三个方面观
察它们.具体方法为:
(1) 确定主视图的位置,画出主视图;
在主视图正下方画出俯视图,注意与主视图“长对正”;
在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
为表示圆柱、圆锥等的对称轴,规定在视图中加画
点划线( )表示对称轴.
分析:
探索新知
如图所示.
解:
探索新知
总 结
不论是画单个几何体的三视图还是组合几何体的
三视图,都必须注意两点:一是遵循“长对正,高平
齐,宽相等”的原则;二是看得见的轮廓线画成实线,
看不见的轮廓线画成虚线.
探索新知
例3 一画出如图所示的支架(一种小零件) 的三视图,其中支架的两个台阶的高度和宽度相等.
支架的形状是由两个大
小不等的长方体 构成的
组合体.画三视图时要注
意这两个长方体的上下、
前后位置关系.
分析:
探索新知
解:下图是支架的三视图.
探索新知
总 结
画组合体的三视图时,构成组合体的各部分的
视图也要遵 守“长对正,高平齐, 宽相等”的规律.
典题精讲
1
画出如图所示的正三棱柱、圆锥、半球的三视图.
解:(1)正三棱柱的三视
图如图所示.
典题精讲
(2)圆锥的三视图如图所示.
(3)半球的三视图如图所示.
典题精讲
2
下面关于正六棱柱的视图(主视图、左视图、俯视图)
中,画法错误的是( )
A
典题精讲
3
如图,添线补全各
物体的三视图.
解:(1)主视图正确,左视图、
俯视图如图①所示.
(2)主视图正确,左视图、
俯视图如图②所示.
易错提醒
如图是一个由3个相同的正方体组成的立体图形,它的三视图是( )
易错点:画图时忽视被遮挡部分的轮廓线.
A
学以致用
小试牛刀
将如图所示的图形绕AB 边所在直线旋转一周,所得几何体的俯视图为( )
B
1
小试牛刀
画出如图所示立体图形的三
视图.(相当于在桌面的中间
靠后放着一个盒子)
解:三视图如图所示.
2
小试牛刀
3
如图是一个正六棱柱的主视图和左视图,则图中a 的值为( )
A.2 B. C.2 D.1
B
小试牛刀
4
如图是一个直四棱柱及其主视图和俯视图(等腰梯形).
(1)根据图中所给数据,可求出俯视图(等腰梯形)的高
为________;
(2)在虚线框内画出左视图,
并标出各边的长.
(2)如图所示.
解:
4
小试牛刀
5
画出如图所示的几何体的三种视图.
解:
(1)如图①所示. (2)如图②所示.
小试牛刀
6
如图是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的左视图和俯视图(用阴影表示);
(2)如果在这个几何体上再添加一些相同的小正方体,
并保持这个几何体的俯视图和左视图不变,那么最
多可以再添加几个小正方体?
小试牛刀
(1)画图如图所示.
(2)最多可再添加4个小正方体.
解:
课堂小结
课堂小结
1. 三视图是指主视图、左视图与俯视图.
2. 画物体三视图的具体步骤为:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图的正右方画出左视图,注意与主视图“高平齐”与俯视
图“宽相等”.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.2 三 视 图
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
这首诗教会了我们怎样观察物体(横看、侧看、
近看、身处其中看),这类似于本节课所研究的内
容——三视图.
新课精讲
探索新知
1
知识点
几何体的三视图
当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图(view). 视图可以看作物体在某一方向光线下的正投影.对于同一个物体, 如果从不同方向观察,所得到的视图可能不同.如图是同一本书的三个不同的视图.
探索新知
我们知道,单一的视图通常只能反映物体一个方
面的形状.为了全面地反映物体的形状,生产实践中往
往采用多个视图来反映同一物体不同方面的形状.例如
图中右侧的三个视图,可以多方面反映飞机的形状.
探索新知
如下图,我们用三个互相垂直的平面(例如墙角处的三面墙壁) 作为投影面,其中正对着我们的平面叫做正面,下方的平面叫做水平面,右边的平面叫做侧面.对一个物体(例如一个长方体) 在三个投影面内进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图; 在侧面内得到的由左向右观察物体的视图,叫做左视图.
探索新知
探索新知
例1 如图所示的几何体的左视图是( )
左视图是从物体的左面看到的视图,从圆柱的左
边向右边看,看到的是一个矩形,故选C.
导引:
C
探索新知
总 结
单个几何体的三视图直接根据常见的几何体三视图中识别.
典题精讲
把图中的几何体与它们对应的三视图用线连接起来.
1
典题精讲
如图是由四个相同的小正方体组成的几何体,则它的主视图为( )
2
A
典题精讲
如图是一个空心圆柱体,它的左视图是( )
3
B
典题精讲
如图是一个水平放置的圆柱形物体,中间有一个细棒,则此几何体的俯视图是( )
4
C
典题精讲
下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
5
C
典题精讲
如图所示的几何体为圆台,其俯视图正确的是( )
6
C
典题精讲
下面几个几何体中,其主视图不是中心对称图形的是( )
7
C
探索新知
2
知识点
画几何体的三视图
如图(2),将三个投影面展开在一个平面内,得到这一物体的一张三视图(由主视图、俯视图和左视图组成).三视图中的各视图,分别从不 同方面表示物体的形状,三者合起来能够较全面地反映物体的形状.
探索新知
主视图
左视图
俯视图
长
宽
高
长
高
宽
高
长
宽
长对正,主视俯视长相等且对正
高平齐,俯视左视宽相等且对应
探索新知
例2 画出图中基本几何体的三视图
探索新知
画这些基本几何体的三视图时,要注意从三个方面观
察它们.具体方法为:
(1) 确定主视图的位置,画出主视图;
在主视图正下方画出俯视图,注意与主视图“长对正”;
在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
为表示圆柱、圆锥等的对称轴,规定在视图中加画
点划线( )表示对称轴.
分析:
探索新知
如图所示.
解:
探索新知
总 结
不论是画单个几何体的三视图还是组合几何体的
三视图,都必须注意两点:一是遵循“长对正,高平
齐,宽相等”的原则;二是看得见的轮廓线画成实线,
看不见的轮廓线画成虚线.
探索新知
例3 一画出如图所示的支架(一种小零件) 的三视图,其中支架的两个台阶的高度和宽度相等.
支架的形状是由两个大
小不等的长方体 构成的
组合体.画三视图时要注
意这两个长方体的上下、
前后位置关系.
分析:
探索新知
解:下图是支架的三视图.
探索新知
总 结
画组合体的三视图时,构成组合体的各部分的
视图也要遵 守“长对正,高平齐, 宽相等”的规律.
典题精讲
1
画出如图所示的正三棱柱、圆锥、半球的三视图.
解:(1)正三棱柱的三视
图如图所示.
典题精讲
(2)圆锥的三视图如图所示.
(3)半球的三视图如图所示.
典题精讲
2
下面关于正六棱柱的视图(主视图、左视图、俯视图)
中,画法错误的是( )
A
典题精讲
3
如图,添线补全各
物体的三视图.
解:(1)主视图正确,左视图、
俯视图如图①所示.
(2)主视图正确,左视图、
俯视图如图②所示.
易错提醒
如图是一个由3个相同的正方体组成的立体图形,它的三视图是( )
易错点:画图时忽视被遮挡部分的轮廓线.
A
学以致用
小试牛刀
将如图所示的图形绕AB 边所在直线旋转一周,所得几何体的俯视图为( )
B
1
小试牛刀
画出如图所示立体图形的三
视图.(相当于在桌面的中间
靠后放着一个盒子)
解:三视图如图所示.
2
小试牛刀
3
如图是一个正六棱柱的主视图和左视图,则图中a 的值为( )
A.2 B. C.2 D.1
B
小试牛刀
4
如图是一个直四棱柱及其主视图和俯视图(等腰梯形).
(1)根据图中所给数据,可求出俯视图(等腰梯形)的高
为________;
(2)在虚线框内画出左视图,
并标出各边的长.
(2)如图所示.
解:
4
小试牛刀
5
画出如图所示的几何体的三种视图.
解:
(1)如图①所示. (2)如图②所示.
小试牛刀
6
如图是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的左视图和俯视图(用阴影表示);
(2)如果在这个几何体上再添加一些相同的小正方体,
并保持这个几何体的俯视图和左视图不变,那么最
多可以再添加几个小正方体?
小试牛刀
(1)画图如图所示.
(2)最多可再添加4个小正方体.
解:
课堂小结
课堂小结
1. 三视图是指主视图、左视图与俯视图.
2. 画物体三视图的具体步骤为:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图的正右方画出左视图,注意与主视图“高平齐”与俯视
图“宽相等”.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
