【班海精品】人教版(新)九下-29.3 课题学习 制作立体模型【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-29.3 课题学习 制作立体模型【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览







文档简介
(共31张PPT)
29.3 课题学习 制作立体模型
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
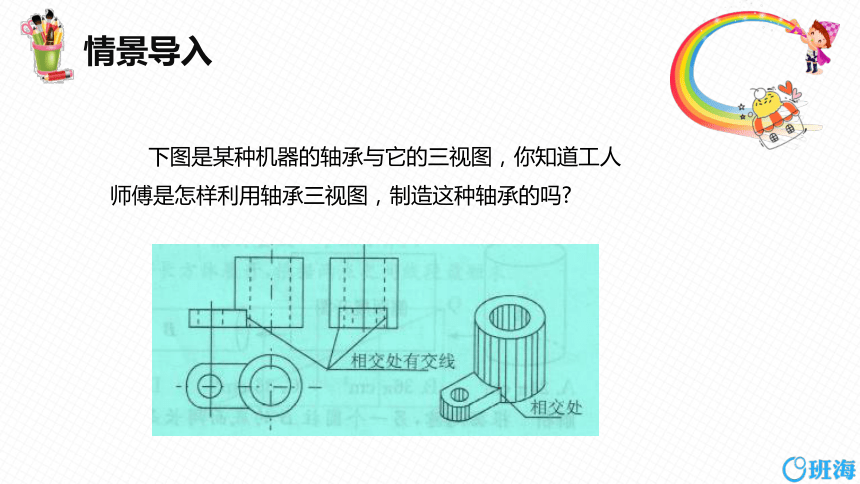
下图是某种机器的轴承与它的三视图,你知道工人
师傅是怎样利用轴承三视图,制造这种轴承的吗
新课精讲
探索新知
1
知识点
由三视图制作立体模型
观察三视图,并综合考虑各视图表达的含义以及
视图间的联系,可以想象出三视图所表示的立体图形
的形状,这是由视图转化为立体图形的过程.下面我们
动手实践,体会一下这个过程.
探索新知
一、课题学习目的
通过由三视图制作立体模型的实践活动,体验平面
图形向立体图形转化的过程,体会用三视图表示立体图
形的作用,进一步感受立体图形与平面图形之间的联系.
二、工具准备
刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等.
探索新知
三、具体活动
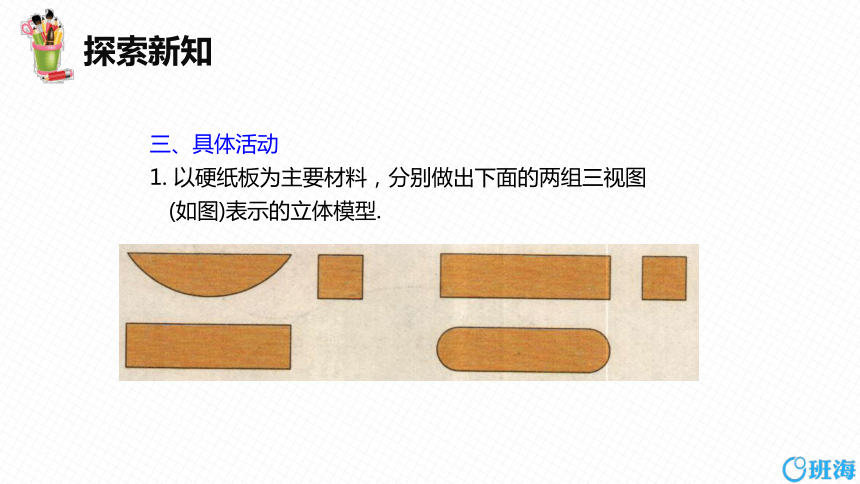
1. 以硬纸板为主要材料,分别做出下面的两组三视图
(如图)表示的立体模型.
探索新知
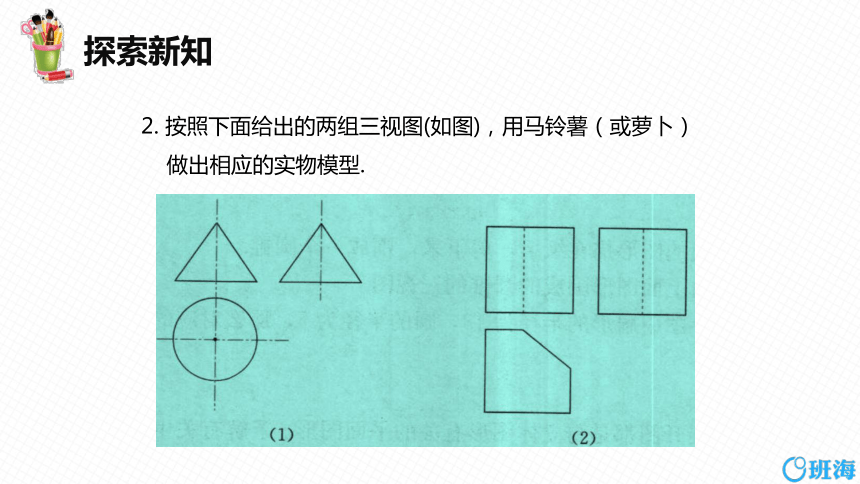
2. 按照下面给出的两组三视图(如图),用马铃薯(或萝卜)
做出相应的实物模型.
探索新知
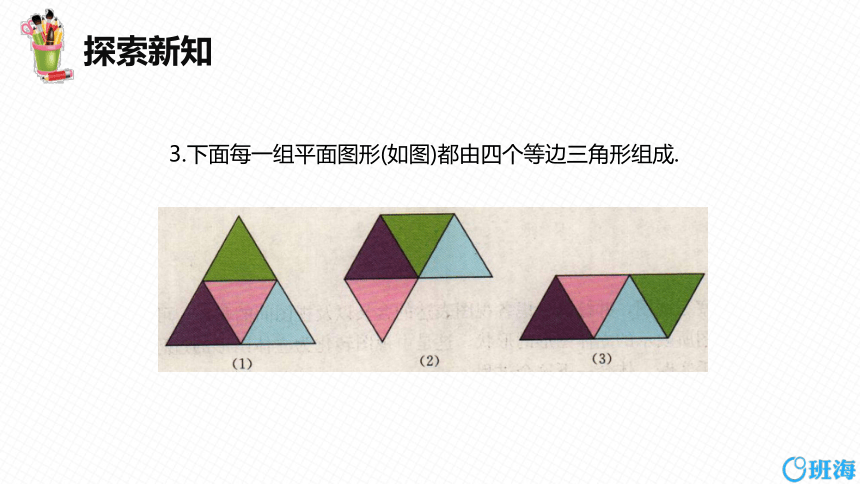
3.下面每一组平面图形(如图)都由四个等边三角形组成.
探索新知
其中哪些可以折叠成三棱锥?把上面的图形描在纸上,
剪下来,叠一 叠,验证你的结论.
画出由上面图形能折叠成的三棱锥的三视图,并指出
三视图中是怎样体现“长对正,高平齐,宽相等”的.
如果上图中小三角形的边长为1,那么对应的三棱锥
的表面积是多少?
探索新知
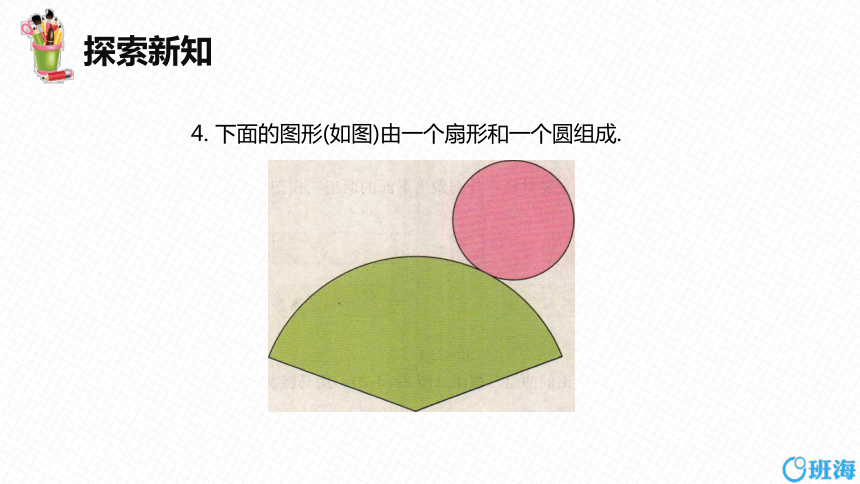
4. 下面的图形(如图)由一个扇形和一个圆组成.
探索新知
把上面的图形描在纸上,剪下来,围成一个圆锥.
画出由上面图形围成的圆锥的三视图.
如果上图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少?
探索新知
四、课题拓广
三视图、展开图都是与立体图形有关的平面图形.
了解有关生产实际,结合具体例子,写一篇短文介绍
三视图、展开图的应用.
探索新知
总 结
根据视图制作立体图形模型的一般步骤:
通过视图想象物体的形状,将平面图形转化为立体图形,然后分组交流、合作、制作立体模型.
注意:一般以硬纸板作为主要原料,或易切割的物体.
探索新知
例1 一个几何体的展开图如图,把它折叠后能构成的立
体图形是( )
A.三棱柱 B.三棱锥
C.四棱柱 D.四棱锥
这个几何体的展开图是由三个长
方形和两个三角形组成,这个几
何体是三棱柱.故选A.
导引:
A
探索新知
总 结
在解决此类问题时,需要熟知常见几何体的平面展开图,从而由展开图推出几何体的形状,也可用尝试操作的办法来判断.
探索新知
例2 如图,是一个几何体的三视图.
(1)写出此几何体的名称;
(2)求此几何体的表面积S.
(1)主视图和左视图为三角
形的几何体一定为锥体,
俯视图为圆,应为圆锥;
导引:
探索新知
(2)易得圆锥的底面半径,利用高,底面半径,圆锥母
线构成的直角三角形可求得圆锥的母线长,圆锥的
表面积=底面积+侧面积=π×底面半径2+π×底
面半径×母线长,把相关数值代入即可求解.
探索新知
(1)圆锥.
(2)由图可知,圆锥高为8 cm,底面直径为12 cm,
易求得母线长为10 cm.
∴S=πr2+πrl=36π+60π=96π(cm2).
解:
探索新知
总 结
此类问题分两步进行:
第一,确定几何体的形状;
第二,根据已知数据进行计算.
典题精讲
观察三视图,并综合考虑各视图表达的含义及视图
间的联系,可以想象出三视图所表示的__________
的形状.这是由_______化为___________的过程.
1
立体图形
视图
立体图形
学以致用
小试牛刀
1 按照下面给出的两组视图(如图所示):选取合适的
材料制成相应的实物模型,写出制作流程.
小试牛刀
(1)是圆锥,制作流程:
①用刻度尺度量其底面圆的半径r,高h,母线长l;
②用小刀把萝卜削成一个底面圆半径为r,高为h 的圆柱体;
③把圆柱体加工成如图①所示的模型.
(2)为正方体截去一个三棱柱,是五棱柱.制作流程:
①用刻度尺度量正方体的棱长a,被截去的三棱柱的底面为直角三角形,一条直角边长为b,另一条直角边长为c;
②用小刀将萝卜削成一个正方体,棱长为a;
③在以这个正方体为坯的基准上再加工,使其截出一个三棱柱,三棱柱底面上直角三角形的两直角边长分别为b 和c.一个立体图形做成,如图②所示.
解:
小试牛刀
由三视图描述几何体,图(1)是圆锥,图(2)为正方体截去一个三棱柱,是五棱柱.
点拨:
规律总结:
(1)选取材料要易切割;(2)由三视图画出几何体模型,再将模型上有关尺寸用刻度尺量出;(3)制作毛坯,再从毛坯中加工成符合条件的立体模型.
小试牛刀
小明利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模
型如图所示,有关数据已标注在图上.
(1)请画出该立体模型的三视图和表面展开图;
(2)做该笔筒至少要用多少平方厘米废纸板?
小试牛刀
(1)三视图和表面展开图如图(表面展开图画法不唯一):
(2)侧面面积为(6+8+10)×14=336(cm2),
直角三角形的面积为 ×8×6=24(cm2),
表面积为336+24=360(cm2).
所以做该笔筒至少要用废纸板360 cm2.
解:
课堂小结
课堂小结
根据三视图制作立体模型,需要先由三视图想出立体图形,再画出平面展开图并折合展开图为立体图形或先分别画出立体图形的各个侧面,再将它们粘合起来.
2.由三视图想出立体图形,将想出来的立体图形直接刻制出来.
3.由展开图想出立体图形,并通过制作模型检验自己的想象正确与否.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
29.3 课题学习 制作立体模型
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下图是某种机器的轴承与它的三视图,你知道工人
师傅是怎样利用轴承三视图,制造这种轴承的吗
新课精讲
探索新知
1
知识点
由三视图制作立体模型
观察三视图,并综合考虑各视图表达的含义以及
视图间的联系,可以想象出三视图所表示的立体图形
的形状,这是由视图转化为立体图形的过程.下面我们
动手实践,体会一下这个过程.
探索新知
一、课题学习目的
通过由三视图制作立体模型的实践活动,体验平面
图形向立体图形转化的过程,体会用三视图表示立体图
形的作用,进一步感受立体图形与平面图形之间的联系.
二、工具准备
刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等.
探索新知
三、具体活动
1. 以硬纸板为主要材料,分别做出下面的两组三视图
(如图)表示的立体模型.
探索新知
2. 按照下面给出的两组三视图(如图),用马铃薯(或萝卜)
做出相应的实物模型.
探索新知
3.下面每一组平面图形(如图)都由四个等边三角形组成.
探索新知
其中哪些可以折叠成三棱锥?把上面的图形描在纸上,
剪下来,叠一 叠,验证你的结论.
画出由上面图形能折叠成的三棱锥的三视图,并指出
三视图中是怎样体现“长对正,高平齐,宽相等”的.
如果上图中小三角形的边长为1,那么对应的三棱锥
的表面积是多少?
探索新知
4. 下面的图形(如图)由一个扇形和一个圆组成.
探索新知
把上面的图形描在纸上,剪下来,围成一个圆锥.
画出由上面图形围成的圆锥的三视图.
如果上图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少?
探索新知
四、课题拓广
三视图、展开图都是与立体图形有关的平面图形.
了解有关生产实际,结合具体例子,写一篇短文介绍
三视图、展开图的应用.
探索新知
总 结
根据视图制作立体图形模型的一般步骤:
通过视图想象物体的形状,将平面图形转化为立体图形,然后分组交流、合作、制作立体模型.
注意:一般以硬纸板作为主要原料,或易切割的物体.
探索新知
例1 一个几何体的展开图如图,把它折叠后能构成的立
体图形是( )
A.三棱柱 B.三棱锥
C.四棱柱 D.四棱锥
这个几何体的展开图是由三个长
方形和两个三角形组成,这个几
何体是三棱柱.故选A.
导引:
A
探索新知
总 结
在解决此类问题时,需要熟知常见几何体的平面展开图,从而由展开图推出几何体的形状,也可用尝试操作的办法来判断.
探索新知
例2 如图,是一个几何体的三视图.
(1)写出此几何体的名称;
(2)求此几何体的表面积S.
(1)主视图和左视图为三角
形的几何体一定为锥体,
俯视图为圆,应为圆锥;
导引:
探索新知
(2)易得圆锥的底面半径,利用高,底面半径,圆锥母
线构成的直角三角形可求得圆锥的母线长,圆锥的
表面积=底面积+侧面积=π×底面半径2+π×底
面半径×母线长,把相关数值代入即可求解.
探索新知
(1)圆锥.
(2)由图可知,圆锥高为8 cm,底面直径为12 cm,
易求得母线长为10 cm.
∴S=πr2+πrl=36π+60π=96π(cm2).
解:
探索新知
总 结
此类问题分两步进行:
第一,确定几何体的形状;
第二,根据已知数据进行计算.
典题精讲
观察三视图,并综合考虑各视图表达的含义及视图
间的联系,可以想象出三视图所表示的__________
的形状.这是由_______化为___________的过程.
1
立体图形
视图
立体图形
学以致用
小试牛刀
1 按照下面给出的两组视图(如图所示):选取合适的
材料制成相应的实物模型,写出制作流程.
小试牛刀
(1)是圆锥,制作流程:
①用刻度尺度量其底面圆的半径r,高h,母线长l;
②用小刀把萝卜削成一个底面圆半径为r,高为h 的圆柱体;
③把圆柱体加工成如图①所示的模型.
(2)为正方体截去一个三棱柱,是五棱柱.制作流程:
①用刻度尺度量正方体的棱长a,被截去的三棱柱的底面为直角三角形,一条直角边长为b,另一条直角边长为c;
②用小刀将萝卜削成一个正方体,棱长为a;
③在以这个正方体为坯的基准上再加工,使其截出一个三棱柱,三棱柱底面上直角三角形的两直角边长分别为b 和c.一个立体图形做成,如图②所示.
解:
小试牛刀
由三视图描述几何体,图(1)是圆锥,图(2)为正方体截去一个三棱柱,是五棱柱.
点拨:
规律总结:
(1)选取材料要易切割;(2)由三视图画出几何体模型,再将模型上有关尺寸用刻度尺量出;(3)制作毛坯,再从毛坯中加工成符合条件的立体模型.
小试牛刀
小明利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模
型如图所示,有关数据已标注在图上.
(1)请画出该立体模型的三视图和表面展开图;
(2)做该笔筒至少要用多少平方厘米废纸板?
小试牛刀
(1)三视图和表面展开图如图(表面展开图画法不唯一):
(2)侧面面积为(6+8+10)×14=336(cm2),
直角三角形的面积为 ×8×6=24(cm2),
表面积为336+24=360(cm2).
所以做该笔筒至少要用废纸板360 cm2.
解:
课堂小结
课堂小结
根据三视图制作立体模型,需要先由三视图想出立体图形,再画出平面展开图并折合展开图为立体图形或先分别画出立体图形的各个侧面,再将它们粘合起来.
2.由三视图想出立体图形,将想出来的立体图形直接刻制出来.
3.由展开图想出立体图形,并通过制作模型检验自己的想象正确与否.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
