【班海精品】人教版(新)九下-26.1 反比例函数 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-26.1 反比例函数 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览








文档简介
(共37张PPT)
26.1 反比例函数
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
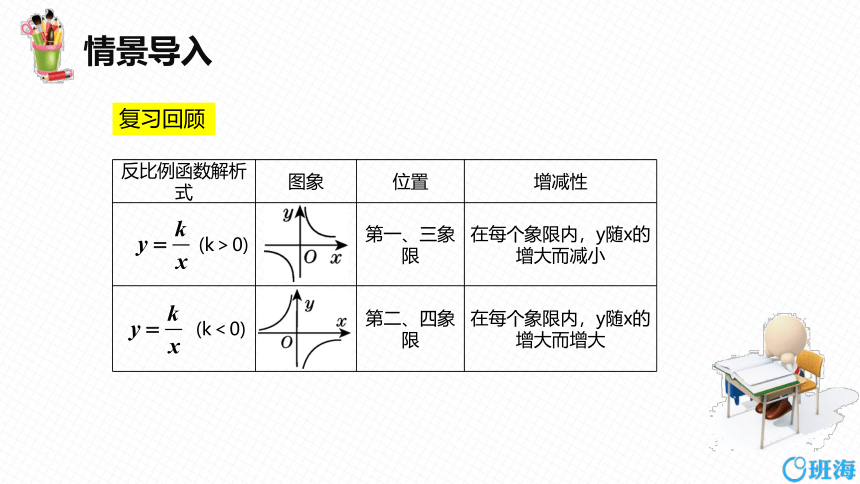
反比例函数解析式 图象 位置 增减性
(k>0) 第一、三象限 在每个象限内,y随x的增大而减小
(k<0) 第二、四象限 在每个象限内,y随x的增大而增大
新课精讲
探索新知
1
知识点
反比例函数中k 的几何性质
双曲线的几何特性:过双曲线 上的任意一点
向两坐标轴作垂线,与两坐
标轴围成的矩形面积等于
|k|,连接该点与原点,还
可得出两个直角三角形,
这两个直角三角形的面积
都等于 .
探索新知
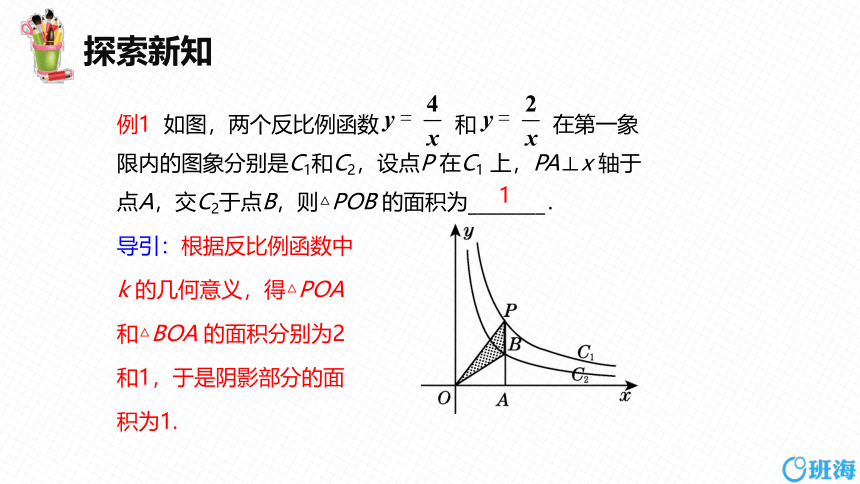
例1 如图,两个反比例函数 和 在第一象限内的图象分别是C1和C2,设点P 在C1 上,PA⊥x 轴于点A,交C2于点B,则△POB 的面积为________.
导引:根据反比例函数中
k 的几何意义,得△POA
和△BOA 的面积分别为2
和1,于是阴影部分的面
积为1.
1
探索新知
总 结
求阴影部分面积的方法:
当它无法直接求出时,一般都采用“转化”的方法,将它转化为易求图形面积的和或差来进行计算.如本例就是将阴影部分面积转化为两个与比例系数相关的特殊三角形的面积的差来求,要注意转化思想的运用.
典题精讲
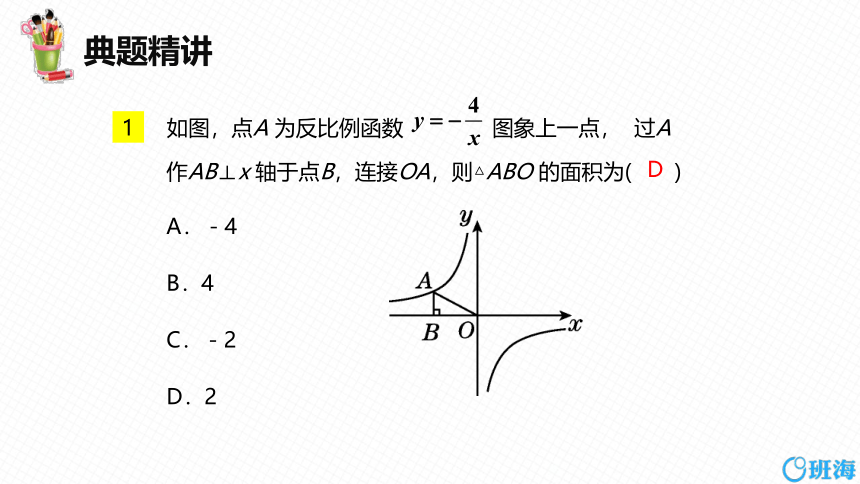
如图,点A 为反比例函数 图象上一点, 过A
作AB⊥x 轴于点B,连接OA,则△ABO 的面积为( )
A.-4
B.4
C.-2
D.2
D
典题精讲
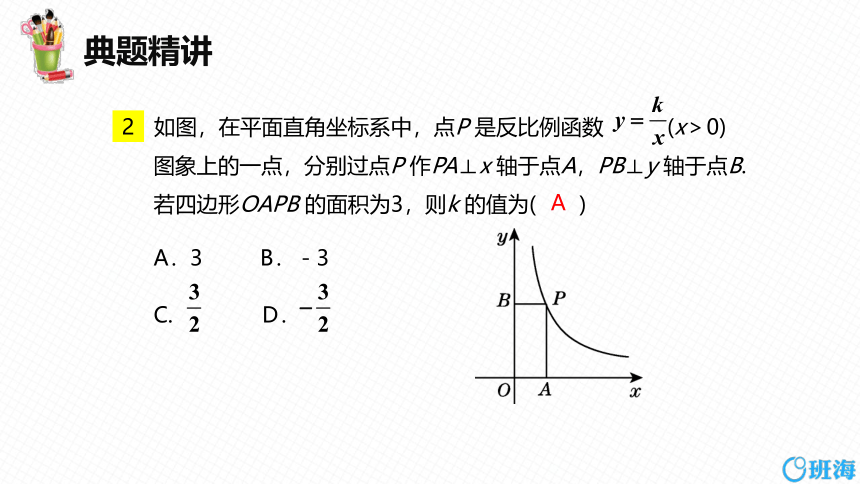
如图,在平面直角坐标系中,点P 是反比例函数 (x>0)
图象上的一点,分别过点P 作PA⊥x 轴于点A,PB⊥y 轴于点B.
若四边形OAPB 的面积为3,则k 的值为( )
A.3 B.-3
C. D.
A
典题精讲
一次函数y=kx+b (k≠0)的图象经过A (-1,-4),
B (2,2)两点,P 为反比例函数 图象上一动点,
O 为坐标原点,过点P 作y 轴的垂线,垂足为C,则△PCO
的面积为( )
A.2 B.4
C.8 D.不确定
A
探索新知
2
知识点
反比例函数图象的对称性
反比例函数的图象关于原点成中心对称,也就是把它的图象旋转180°与原图形重合,这是反比例函数的一个重要性质,就常用来求点的坐标和图形的面积等
探索新知
例2 如图,在直角坐标系xOy 中,直线y=mx 与双曲线
相交于A(-1,a ),B 两点,BC⊥x 轴,垂足为C,△AOC
的面积是1.
(1)求m,n 的值;
(2)求直线AC 对应的函数解析式.
探索新知
导引:(1)由题意,根据对称性得到点B 的横坐标为1,确定
出点C 的坐标,根据△AOC 的面积求出点A 的纵坐标,
确定出点A 的坐标,将点A 的坐标代入正比例函数与
反比例函数解析式,即可求出m 与n 的值;
(2)设直线AC 对应的函数解析式为y=kx+b,将A,C
两点坐标分别代入求出k 与b 的值,即可确定出直线
AC 对应的函数解析式.
探索新知
解:(1)∵直线 y=mx 与双曲线 相交于A (-1,a ),
B 两点,
∴B 点横坐标为1.
∴C (1,0).
∵△AOC 的面积为1,
∴ ×a×1=1,∴a=2,
∴A (-1,2).
将A(-1,2)的坐标代入y=mx,
可得m=-2,n=-2.
探索新知
(2)设直线AC 对应的函数解析式为y=kx+b,
∵直线 y=kx+b 经过点A (-1,2),C (1,0),
∴ 解得
∴直线AC 对应的函数解析式为y=-x+1.
探索新知
总 结
反比例函数与正比例函数的图象都是中心对称图形,所以在同一坐标系中,两个函数图象的两个交点关于原点对称.
典题精讲
下列给出的函数中,其图象是中心对称图形的是( )
①函数 y=x;②函数 y=x 2;③函数
A.①② B.②③
C.①③ D.都不是
C
2 已知P 为函数 的图象上一点,且点P 到原点
的距离为2,则符合条件的点P 有( )
A.0个 B.2个
C.4个 D.无数个
B
典题精讲
3 对于函数 ,下列说法错误的是 ( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称
图形
C.当x >0时,y 随x 的增大而增大
D.当x <0时,y 随x 的增大而减小
C
易错提醒
如图,面积为5的矩形OABC 的一个顶点B 在反比例函数
y= 的图象上,另三点在坐标轴上,则k=______.
易错点:已知图形面积求反比例函数比例系数k的值时,易忽视图象的位置.
-5
学以致用
小试牛刀
1 如图,在直角坐标系中,点A 在函数 (x>0)的图象上,
AB⊥x 轴于点B,AB 的垂直平分线与y 轴交于点C,与函数
(x>0)的图象交于点D,连接AC,CB,BD,DA,则四
边形ACBD 的面积等于( )
A.2 B.2
C.4 D.4
C
小试牛刀
如图,在平面直角坐标系中,反比例函数 (x>0)的图象与边长
是6的正方形OABC的两边AB,BC分别相交于M,N两点,△OMN的
面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A.6 B.10
C.2 D.2
C
小试牛刀
3 如图,边长为4的正方形ABCD 的对称中心是坐标原点O,
AB∥x 轴,BC∥y 轴,反比例函数 与 的图象
均与正方形ABCD 的边相交,则图中阴影部分的面积之和是
______.
8
小试牛刀
如图,反比例函数y= 的图象与一次函数y=x+b 的
图象交于A,B 两点,点A 和点B 的横坐标分别为1和-2,
这两点的纵坐标之和为1.
(1)求反比例函数的表达式与一次函
数的表达式;
(2)当点C 的坐标为(0,-1)时,求
△ABC 的面积.
小试牛刀
(2)当x=-2时,y=-1,即B (-2,-1).
∴BC=2.
∴S△ABC= BC·( yA-yC )= ×2×[2-(-1)]=3.
解:
(1)由题意,得1+b+(-2)+b=1,解得b=1,
∴一次函数的表达式为y=x+1.
当x=1时,y=x+1=2,即A(1,2).
将A点坐标代入y= ,得 =2,则k=2.
∴反比例函数的表达式为y= .
小试牛刀
如图,点A(3,5)关于原点O 的对称点为点C,分别过点A,C
作y 轴的平行线,与反比例函数y= (0<k<15)的图象交于
点B,D,连接AD,BC,AD与x 轴交于点E (-2,0).
(1)求k 的值;
(2)直接写出阴影部分面积之和.
小试牛刀
解:
(1)设直线AD 对应的函数解析式为y=ax+b.
∵直线AD 过点A(3,5),E (-2,0),
∴ 解得
∴直线AD 对应的函数解析式为y=x+2.
∵点C 与点A(3,5)关于原点对称,
∴点C 的坐标为(-3,-5).
∵CD∥y 轴,∴点D 的横坐标为-3,
把x=-3代入y=x+2得y=-1.
小试牛刀
∴点D 的坐标为(-3,-1).
∵点D 在函数 y= 的图象上,
∴k=(-3)×(-1)=3.
(2)12.
小试牛刀
如图,△ABC 的顶点坐标为A (-2,3),B (-3,1),
C (-1,2),以坐标原点O 为旋转中心,顺时针旋转90°,
得到△A′B′C ′,点B′,C′ 分别是点B,C 的对应点.
(1)求过点B′ 的反比例函数的
解析式;
(2)求线段CC′ 的长.
小试牛刀
解:
(1)B点的坐标为(-3,1),以O 为旋转中心将点B 顺时针旋转90°得到点B ′,
∴点B′ 的坐标为(1,3).
设过点B′ 的反比例函数的解析式为y= ,
∴3= ,解得k=3.
∴过点B′ 的反比例函数的解析
式为y= .
小试牛刀
(2)接OC,OC ′.∵C (-1,2),
∴OC=
∵点C′ 是点C 以坐标原点O 为旋转中心,顺时针旋转90°后得到的对应点,
∴OC ′=OC= ,
∴CC ′=
小试牛刀
将直线y=3x+1向下平移1个单位长度,得到直线y=3x+m.
若反比例函数y= 的图象与直线 y=3x+m 相交于点A,且
点A 的纵坐标是3.
(1)求m 和k 的值;
(2)结合图象求不等式3x+m> 的解集.
小试牛刀
(1)由平移得:y=3x+1-1=3x,∴m=0.
当 y=3时,3x=3,x=1,∴A (1,3).
∴k=1×3=3.
解:
(2)画出正比例函数 y=3x 和反比例函数y= 的图象,如图所示.
由图象得:不等式3x+m> 的解集
为-1<x<0或x>1.
课堂小结
课堂小结
1.反比例函数中k的几何性质:过双曲线 (k≠0)
上任一点向两坐标轴作垂线所得的矩形面积等于|k |;
向一坐标轴作垂线且与原点连线所得的三角形面积等
于 |k |.
2.双曲线关于直线 y=x 和直线 y=-x 成轴对称.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
26.1 反比例函数
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习回顾
反比例函数解析式 图象 位置 增减性
(k>0) 第一、三象限 在每个象限内,y随x的增大而减小
(k<0) 第二、四象限 在每个象限内,y随x的增大而增大
新课精讲
探索新知
1
知识点
反比例函数中k 的几何性质
双曲线的几何特性:过双曲线 上的任意一点
向两坐标轴作垂线,与两坐
标轴围成的矩形面积等于
|k|,连接该点与原点,还
可得出两个直角三角形,
这两个直角三角形的面积
都等于 .
探索新知
例1 如图,两个反比例函数 和 在第一象限内的图象分别是C1和C2,设点P 在C1 上,PA⊥x 轴于点A,交C2于点B,则△POB 的面积为________.
导引:根据反比例函数中
k 的几何意义,得△POA
和△BOA 的面积分别为2
和1,于是阴影部分的面
积为1.
1
探索新知
总 结
求阴影部分面积的方法:
当它无法直接求出时,一般都采用“转化”的方法,将它转化为易求图形面积的和或差来进行计算.如本例就是将阴影部分面积转化为两个与比例系数相关的特殊三角形的面积的差来求,要注意转化思想的运用.
典题精讲
如图,点A 为反比例函数 图象上一点, 过A
作AB⊥x 轴于点B,连接OA,则△ABO 的面积为( )
A.-4
B.4
C.-2
D.2
D
典题精讲
如图,在平面直角坐标系中,点P 是反比例函数 (x>0)
图象上的一点,分别过点P 作PA⊥x 轴于点A,PB⊥y 轴于点B.
若四边形OAPB 的面积为3,则k 的值为( )
A.3 B.-3
C. D.
A
典题精讲
一次函数y=kx+b (k≠0)的图象经过A (-1,-4),
B (2,2)两点,P 为反比例函数 图象上一动点,
O 为坐标原点,过点P 作y 轴的垂线,垂足为C,则△PCO
的面积为( )
A.2 B.4
C.8 D.不确定
A
探索新知
2
知识点
反比例函数图象的对称性
反比例函数的图象关于原点成中心对称,也就是把它的图象旋转180°与原图形重合,这是反比例函数的一个重要性质,就常用来求点的坐标和图形的面积等
探索新知
例2 如图,在直角坐标系xOy 中,直线y=mx 与双曲线
相交于A(-1,a ),B 两点,BC⊥x 轴,垂足为C,△AOC
的面积是1.
(1)求m,n 的值;
(2)求直线AC 对应的函数解析式.
探索新知
导引:(1)由题意,根据对称性得到点B 的横坐标为1,确定
出点C 的坐标,根据△AOC 的面积求出点A 的纵坐标,
确定出点A 的坐标,将点A 的坐标代入正比例函数与
反比例函数解析式,即可求出m 与n 的值;
(2)设直线AC 对应的函数解析式为y=kx+b,将A,C
两点坐标分别代入求出k 与b 的值,即可确定出直线
AC 对应的函数解析式.
探索新知
解:(1)∵直线 y=mx 与双曲线 相交于A (-1,a ),
B 两点,
∴B 点横坐标为1.
∴C (1,0).
∵△AOC 的面积为1,
∴ ×a×1=1,∴a=2,
∴A (-1,2).
将A(-1,2)的坐标代入y=mx,
可得m=-2,n=-2.
探索新知
(2)设直线AC 对应的函数解析式为y=kx+b,
∵直线 y=kx+b 经过点A (-1,2),C (1,0),
∴ 解得
∴直线AC 对应的函数解析式为y=-x+1.
探索新知
总 结
反比例函数与正比例函数的图象都是中心对称图形,所以在同一坐标系中,两个函数图象的两个交点关于原点对称.
典题精讲
下列给出的函数中,其图象是中心对称图形的是( )
①函数 y=x;②函数 y=x 2;③函数
A.①② B.②③
C.①③ D.都不是
C
2 已知P 为函数 的图象上一点,且点P 到原点
的距离为2,则符合条件的点P 有( )
A.0个 B.2个
C.4个 D.无数个
B
典题精讲
3 对于函数 ,下列说法错误的是 ( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称
图形
C.当x >0时,y 随x 的增大而增大
D.当x <0时,y 随x 的增大而减小
C
易错提醒
如图,面积为5的矩形OABC 的一个顶点B 在反比例函数
y= 的图象上,另三点在坐标轴上,则k=______.
易错点:已知图形面积求反比例函数比例系数k的值时,易忽视图象的位置.
-5
学以致用
小试牛刀
1 如图,在直角坐标系中,点A 在函数 (x>0)的图象上,
AB⊥x 轴于点B,AB 的垂直平分线与y 轴交于点C,与函数
(x>0)的图象交于点D,连接AC,CB,BD,DA,则四
边形ACBD 的面积等于( )
A.2 B.2
C.4 D.4
C
小试牛刀
如图,在平面直角坐标系中,反比例函数 (x>0)的图象与边长
是6的正方形OABC的两边AB,BC分别相交于M,N两点,△OMN的
面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A.6 B.10
C.2 D.2
C
小试牛刀
3 如图,边长为4的正方形ABCD 的对称中心是坐标原点O,
AB∥x 轴,BC∥y 轴,反比例函数 与 的图象
均与正方形ABCD 的边相交,则图中阴影部分的面积之和是
______.
8
小试牛刀
如图,反比例函数y= 的图象与一次函数y=x+b 的
图象交于A,B 两点,点A 和点B 的横坐标分别为1和-2,
这两点的纵坐标之和为1.
(1)求反比例函数的表达式与一次函
数的表达式;
(2)当点C 的坐标为(0,-1)时,求
△ABC 的面积.
小试牛刀
(2)当x=-2时,y=-1,即B (-2,-1).
∴BC=2.
∴S△ABC= BC·( yA-yC )= ×2×[2-(-1)]=3.
解:
(1)由题意,得1+b+(-2)+b=1,解得b=1,
∴一次函数的表达式为y=x+1.
当x=1时,y=x+1=2,即A(1,2).
将A点坐标代入y= ,得 =2,则k=2.
∴反比例函数的表达式为y= .
小试牛刀
如图,点A(3,5)关于原点O 的对称点为点C,分别过点A,C
作y 轴的平行线,与反比例函数y= (0<k<15)的图象交于
点B,D,连接AD,BC,AD与x 轴交于点E (-2,0).
(1)求k 的值;
(2)直接写出阴影部分面积之和.
小试牛刀
解:
(1)设直线AD 对应的函数解析式为y=ax+b.
∵直线AD 过点A(3,5),E (-2,0),
∴ 解得
∴直线AD 对应的函数解析式为y=x+2.
∵点C 与点A(3,5)关于原点对称,
∴点C 的坐标为(-3,-5).
∵CD∥y 轴,∴点D 的横坐标为-3,
把x=-3代入y=x+2得y=-1.
小试牛刀
∴点D 的坐标为(-3,-1).
∵点D 在函数 y= 的图象上,
∴k=(-3)×(-1)=3.
(2)12.
小试牛刀
如图,△ABC 的顶点坐标为A (-2,3),B (-3,1),
C (-1,2),以坐标原点O 为旋转中心,顺时针旋转90°,
得到△A′B′C ′,点B′,C′ 分别是点B,C 的对应点.
(1)求过点B′ 的反比例函数的
解析式;
(2)求线段CC′ 的长.
小试牛刀
解:
(1)B点的坐标为(-3,1),以O 为旋转中心将点B 顺时针旋转90°得到点B ′,
∴点B′ 的坐标为(1,3).
设过点B′ 的反比例函数的解析式为y= ,
∴3= ,解得k=3.
∴过点B′ 的反比例函数的解析
式为y= .
小试牛刀
(2)接OC,OC ′.∵C (-1,2),
∴OC=
∵点C′ 是点C 以坐标原点O 为旋转中心,顺时针旋转90°后得到的对应点,
∴OC ′=OC= ,
∴CC ′=
小试牛刀
将直线y=3x+1向下平移1个单位长度,得到直线y=3x+m.
若反比例函数y= 的图象与直线 y=3x+m 相交于点A,且
点A 的纵坐标是3.
(1)求m 和k 的值;
(2)结合图象求不等式3x+m> 的解集.
小试牛刀
(1)由平移得:y=3x+1-1=3x,∴m=0.
当 y=3时,3x=3,x=1,∴A (1,3).
∴k=1×3=3.
解:
(2)画出正比例函数 y=3x 和反比例函数y= 的图象,如图所示.
由图象得:不等式3x+m> 的解集
为-1<x<0或x>1.
课堂小结
课堂小结
1.反比例函数中k的几何性质:过双曲线 (k≠0)
上任一点向两坐标轴作垂线所得的矩形面积等于|k |;
向一坐标轴作垂线且与原点连线所得的三角形面积等
于 |k |.
2.双曲线关于直线 y=x 和直线 y=-x 成轴对称.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
