【班海精品】人教版(新)九下-27.1 图形的相似 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-27.1 图形的相似 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览







文档简介
(共42张PPT)
27.1 图形的相似
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
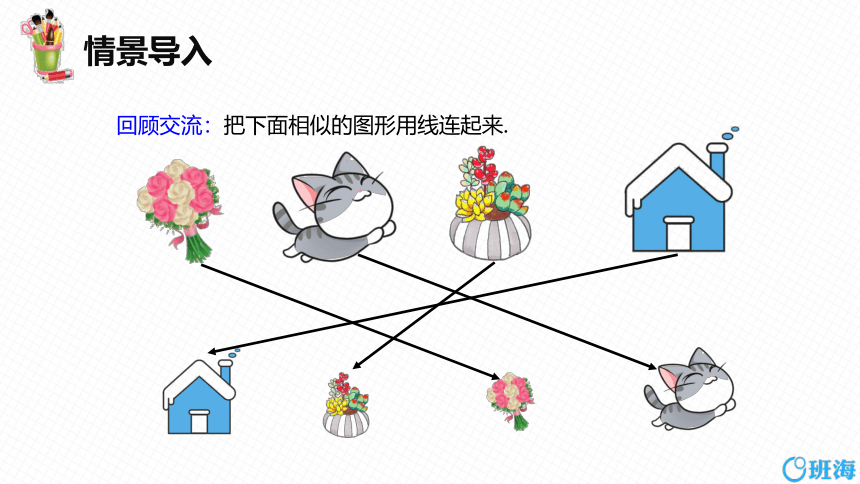
回顾交流:把下面相似的图形用线连起来.
新课精讲
探索新知
1
知识点
相似多边形的定义
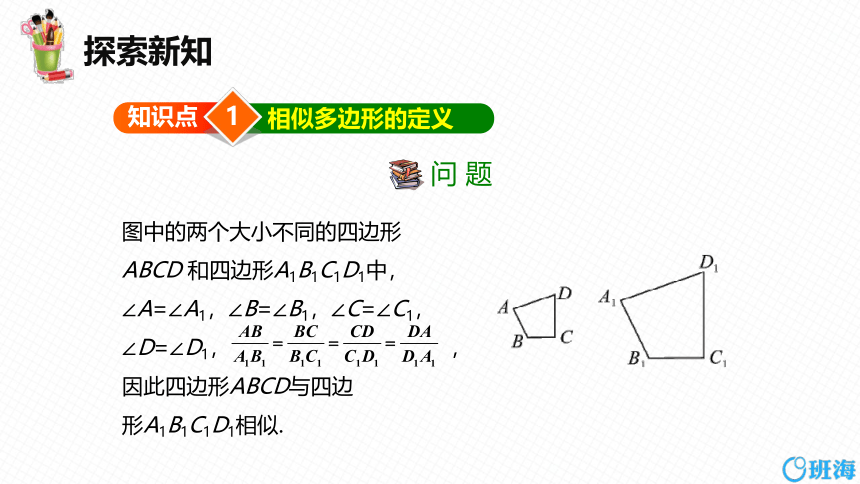
问 题
图中的两个大小不同的四边形
ABCD 和四边形A1B1C1D1中,
∠A=∠A1,∠B=∠B1,∠C=∠C1,
∠D=∠D1, ,
因此四边形ABCD与四边
形A1B1C1D1相似.
探索新知
如果两个多边形的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
定义
判定相似多边形的条件:
(1)所有的角分别相等;
(2)所有的边成比例.
以上的角分别相等,边成比例这两个条件是判定相似多边
形必备的条件,缺一不可.
探索新知
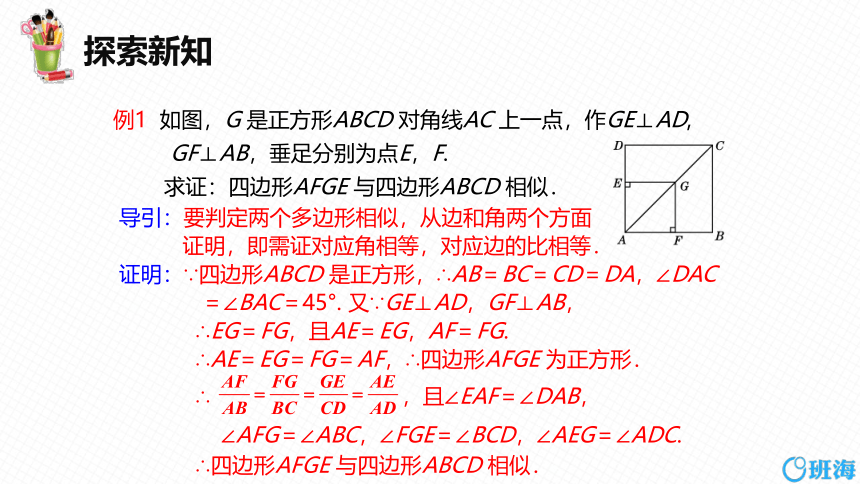
例1 如图,G 是正方形ABCD 对角线AC 上一点,作GE⊥AD,
GF⊥AB,垂足分别为点E,F.
求证:四边形AFGE 与四边形ABCD 相似.
导引:要判定两个多边形相似,从边和角两个方面
证明,即需证对应角相等,对应边的比相等.
证明:∵四边形ABCD 是正方形,∴AB=BC=CD=DA,∠DAC
=∠BAC=45°. 又∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG.
∴AE=EG=FG=AF,∴四边形AFGE 为正方形.
∴ ,且∠EAF=∠DAB,
∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE 与四边形ABCD 相似.
探索新知
总 结
判断两个多边形是否相似,既要看它们的角是否分别相等,也要看边是否成比例,两者缺一不可.例如:两个矩形不一定相似,两个菱形也不一定相似,两个正方形一定相似.
典题精讲
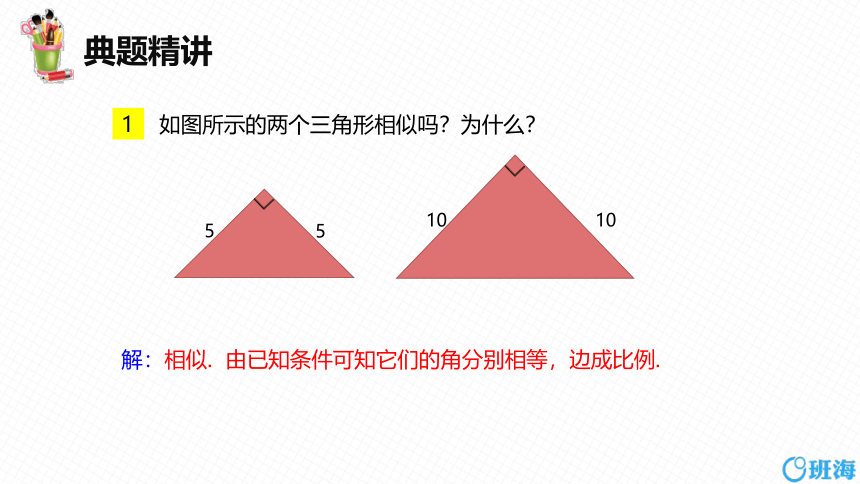
1 如图所示的两个三角形相似吗?为什么?
解:相似. 由已知条件可知它们的角分别相等,边成比例.
5
5
10
10
典题精讲
2 下列说法中正确的是( )
A.对应角相等的多边形一定是相似多边形
B.对应边的比相等的多边形是相似多边形
C.边数相同的多边形是相似多边形
D.对应角相等、对应边成比例的两个边数相同
的多边形是相似多边形
D
典题精讲
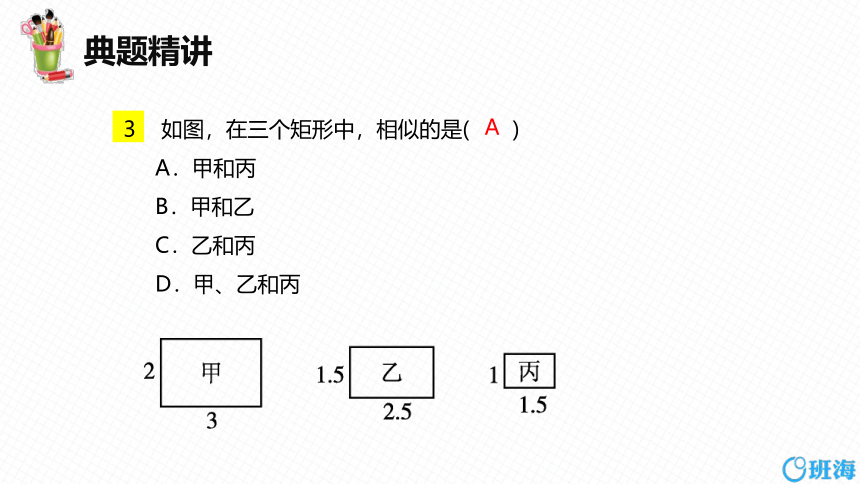
3 如图,在三个矩形中,相似的是( )
A.甲和丙
B.甲和乙
C.乙和丙
D.甲、乙和丙
A
探索新知
2
知识点
相似多边形的性质
相似多边形的性质:
相似多边形的对应边的比相等,对应角相等.
作用:
常用来求相似多边形中未知的边的长度和角的度数.
探索新知
例2 如图,四边形ABCD 和EFGH 相似,求角α,β 的大
小和EF 的长度x.
解:因为四边形ABCD 和EFGH 相
似,所以它们的对应角相等,
由此可得α=∠C=83°, ∠A=∠E=118°.
在四边形ABCD 中,
β=360°-(78°+83°+118°) = 81°.
因为四边形ABCD 和EFGH 相似,所以它们的对应边
成比例,由此可得
解得x =28.
探索新知
总 结
利用相似多边形的性质求边长或角度,关键扣住“对应”二字,找准对应边和对应角是解决问题的关键.需要注意的是对应边是比相等,而对应角是直接相等.
典题精讲
1 如图所示的两个五边形相似,求a,b,c,d 的值.
解:a=3,b=4.5,c=4,d=6.
c
d
2
5
3
6
9
a
7.5
b
典题精讲
若一个三角形的三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为( )
A.15 B.10
C.9 D.3
2
C
如图,正五边形FGHMN 与正五边形ABCDE 相似,若AB:FG=2:3,则下列结论正确的是( )
A.2DE=3MN
B.3DE=2MN
C.3∠A=2∠F
D.2∠A=3∠F
3
B
典题精讲
如图,四边形ABCD 与四边形A1B1C1D1 相似,AB=12,CD=15,A1B1=9,则C1D1的长是( )
A.10
B.12
C.
D.
4
C
典题精讲
如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形的面积是( )
A.2 cm2
B.4 cm2
C.8 cm2
D.16 cm2
5
C
探索新知
3
知识点
相似比
相似比的定义:相似多边形对应边的比称为相似比.
△ABC ∽△A B C
∠A = ∠A
∠B = ∠B
∠C = ∠C
对应角相等
对应边成比例
A B
A B
=
=
B C
B C
A C
A C
= 相似比
若△ABC ∽△A B C
探索新知
导引:相似多边形的对应边的比相等,其比值就是相似比.
解:(1)设AD=x,则DM= . ∵矩形DMNC 与矩形ABCD 相似,
∴x 2=32.
∴x=4 或x=-4 (舍去),即AD 的长为4 .
(2)矩形DMNC 与矩形ABCD 的相似比为
例3 如图,把矩形ABCD 对折,折痕为MN,矩形DMNC 与
矩形ABCD 相似,已知AB=4.
(1)求AD 的长;
(2)求矩形DMNC 与矩形ABCD 的相似比.
探索新知
总 结
利用相似多边形的性质求线段长及相似比的方法:
先找出与已知边、未知边相关的四条对应线段,再通过设未知数并用含未知数的式子表示其中的部分线段,最后通过相似多边形的对应边成比例建立方程进行计算.这种巧用方程思想的方法在相似多边形的计算中经常运用.
典题精讲
如果两个相似多边形的一组对应边长分别为3 cm和2 cm,
那么它们的相似比是( )
A. B. C. D.
C
六边形ABCDEF 与六边形A′B′C′D′E′F ′相似,若对应边AB 与A′B ′的长分别为50 cm和40 cm,则六边形A′B′C′D′E′F ′与六边形ABCDEF 的相似比是( )
A.5:4 B.4:5
C.5:2 D.2:
2
B
易错提醒
一位同学经过研究发现:在等边三角形中,每条边都是相等的,两个等边三角形相似;在正方形中,每条边都是相等的,两个正方形相似.于是他进一步推广,认为如果多边形的各边都相等,那么这样的两个边数相同的多边形相似.你认为这种说法正确吗?为什么?
易错提醒
解:
这种说法不正确.比如,如图所示的两个菱形,每个菱形的边长都是相等的,但它们的各角并不是对应相等的,所以它们不相似.
易错点:对相似多边形定义理解不透而致错.
学以致用
小试牛刀
1 下列四组图形中,一定相似的是( )
A.正方形与矩形
B.正方形与菱形
C.菱形与菱形
D.正五边形与正五边形
D
小试牛刀
两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,
每组中的一个图形在另一个图形的内部,对应边平行,且对应边
之间的距离都相等,那么两个图形不相似的一组是( )
B
小试牛刀
志远要在报纸上刊登广告,一块10 cm×5 cm的长方形版面要付广告费180元,他要把该版面的边长都扩大为原来的3倍,在每平方厘米版面广告费相同的情况下,他该付广告费( )
A.540元 B.1 080元
C.1 620元 D.1 800元
3
C
小试牛刀
4 如图,四边形ABCD 与四边形EFGH 相似,∠A=62°,∠B=70°,∠H=140°,AD=18,EF=15,FG=14,EH=12,求∠G 的度数及AB,BC 的长.
小试牛刀
解:
∵四边形ABCD 与四边形EFGH 相似,
∴∠E=∠A=62°,∠F=∠B=70°,
又∵∠H=140°,∠E+∠F+∠G+∠H=360°,
∴∠G=88°.
∵四边形ABCD 与四边形EFGH 相似,
∴ .
又∵AD=18,EF=15,FG=14,EH=12,
∴AB=22.5,BC=21.
小试牛刀
5 如图,多边形ABCDEF 与多边形A1B1C1D1E1F1相似,其中,A,B,C,D,E,F 的对应点分别为A1,B1,C1,D1,E1,F1,∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F 的度数;
(2)如果多边形ABCDEF 和多
边形A1B1C1D1E1F1的相似比是1∶1.5,
且CD=15 cm,求C1D1的长度.
小试牛刀
(1)∵多边形ABCDEF 和多边形A1B1C1D1E1F1 相似,且∠C
和∠C1,∠D 和∠D1,∠E 和∠E1是对应角,
∴∠C=95°,∠D=135°,∠E=120°.
由多边形内角和定理,知∠F=720°-(135°+120°+ 95°+135°+120°)=115°.
解:
(2) ∵多边形ABCDEF 和多边形A1B1C1D1E1F 1的相似比
是1∶1.5,且CD=15 cm,
∴C1D1=15×1.5=22.5(cm).
小试牛刀
6 如图,将一张长、宽之比为 ∶1的矩形纸ABCD 依次不断对折,可以得到矩形BCFE,AEML,GMFH,LGPN.
(1)判断矩形ABCD,BCFE,AEML,GMFH,LGPN 的长、宽之比是否相等,并说明理由;
(2)你认为这些大小不同的矩形相似吗?
小试牛刀
解:
(1)矩形ABCD,BCFE,AEML,GMFH,LGPN 的长、宽之比相等.理由如下:
设矩形纸的宽BC=a,长AB= a,
则有BE= a,AE= a,ME= ,MF= ,
HF= a,LG= a,LN= ,
∴
小试牛刀
∴五个矩形的长、宽之比相等.
(2)这些大小不同的矩形都相似.
小试牛刀
7 一个用钢筋焊接的三角形的三边长分别是20 cm,60 cm,50 cm,现要做一个与其相似的钢筋三角形.因为只有长为30 cm和50 cm的两根钢筋,所以要求以其中一根为一边,从另一根上截下两段(允许有余料)作为另外两边,问:有几种截法?请指出用余料最少的截法截出的三边长分别为多少.
小试牛刀
解:
若截30 cm长的钢筋,设截成的两段长分别为a cm和b cm
(a<b),则有 ,解得a= ,b= .
∵a+b= + = >30,
∴此截法不成立.
若截50 cm长的钢筋,设截成的两段长分别为x cm和y cm
(x<y ),则有① ,解得x=12,y=36.
∵x+y=12+36=48<50,∴此截法成立.
小试牛刀
② ,解得x=10,y=25.
∵x+y=10+25=35<50,∴此截法成立.
因此有两种截法.
∵50-48=2(cm),50-35=15(cm),
∴用余料最少的截法截出的三边长分别为12 cm,30 cm,36 cm.
课堂小结
课堂小结
相似相似形的性质:
(1)对应角 ;
(2)对应边的比等于 ;
相等
相似比
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.1 图形的相似
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾交流:把下面相似的图形用线连起来.
新课精讲
探索新知
1
知识点
相似多边形的定义
问 题
图中的两个大小不同的四边形
ABCD 和四边形A1B1C1D1中,
∠A=∠A1,∠B=∠B1,∠C=∠C1,
∠D=∠D1, ,
因此四边形ABCD与四边
形A1B1C1D1相似.
探索新知
如果两个多边形的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
定义
判定相似多边形的条件:
(1)所有的角分别相等;
(2)所有的边成比例.
以上的角分别相等,边成比例这两个条件是判定相似多边
形必备的条件,缺一不可.
探索新知
例1 如图,G 是正方形ABCD 对角线AC 上一点,作GE⊥AD,
GF⊥AB,垂足分别为点E,F.
求证:四边形AFGE 与四边形ABCD 相似.
导引:要判定两个多边形相似,从边和角两个方面
证明,即需证对应角相等,对应边的比相等.
证明:∵四边形ABCD 是正方形,∴AB=BC=CD=DA,∠DAC
=∠BAC=45°. 又∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG.
∴AE=EG=FG=AF,∴四边形AFGE 为正方形.
∴ ,且∠EAF=∠DAB,
∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE 与四边形ABCD 相似.
探索新知
总 结
判断两个多边形是否相似,既要看它们的角是否分别相等,也要看边是否成比例,两者缺一不可.例如:两个矩形不一定相似,两个菱形也不一定相似,两个正方形一定相似.
典题精讲
1 如图所示的两个三角形相似吗?为什么?
解:相似. 由已知条件可知它们的角分别相等,边成比例.
5
5
10
10
典题精讲
2 下列说法中正确的是( )
A.对应角相等的多边形一定是相似多边形
B.对应边的比相等的多边形是相似多边形
C.边数相同的多边形是相似多边形
D.对应角相等、对应边成比例的两个边数相同
的多边形是相似多边形
D
典题精讲
3 如图,在三个矩形中,相似的是( )
A.甲和丙
B.甲和乙
C.乙和丙
D.甲、乙和丙
A
探索新知
2
知识点
相似多边形的性质
相似多边形的性质:
相似多边形的对应边的比相等,对应角相等.
作用:
常用来求相似多边形中未知的边的长度和角的度数.
探索新知
例2 如图,四边形ABCD 和EFGH 相似,求角α,β 的大
小和EF 的长度x.
解:因为四边形ABCD 和EFGH 相
似,所以它们的对应角相等,
由此可得α=∠C=83°, ∠A=∠E=118°.
在四边形ABCD 中,
β=360°-(78°+83°+118°) = 81°.
因为四边形ABCD 和EFGH 相似,所以它们的对应边
成比例,由此可得
解得x =28.
探索新知
总 结
利用相似多边形的性质求边长或角度,关键扣住“对应”二字,找准对应边和对应角是解决问题的关键.需要注意的是对应边是比相等,而对应角是直接相等.
典题精讲
1 如图所示的两个五边形相似,求a,b,c,d 的值.
解:a=3,b=4.5,c=4,d=6.
c
d
2
5
3
6
9
a
7.5
b
典题精讲
若一个三角形的三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为( )
A.15 B.10
C.9 D.3
2
C
如图,正五边形FGHMN 与正五边形ABCDE 相似,若AB:FG=2:3,则下列结论正确的是( )
A.2DE=3MN
B.3DE=2MN
C.3∠A=2∠F
D.2∠A=3∠F
3
B
典题精讲
如图,四边形ABCD 与四边形A1B1C1D1 相似,AB=12,CD=15,A1B1=9,则C1D1的长是( )
A.10
B.12
C.
D.
4
C
典题精讲
如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形的面积是( )
A.2 cm2
B.4 cm2
C.8 cm2
D.16 cm2
5
C
探索新知
3
知识点
相似比
相似比的定义:相似多边形对应边的比称为相似比.
△ABC ∽△A B C
∠A = ∠A
∠B = ∠B
∠C = ∠C
对应角相等
对应边成比例
A B
A B
=
=
B C
B C
A C
A C
= 相似比
若△ABC ∽△A B C
探索新知
导引:相似多边形的对应边的比相等,其比值就是相似比.
解:(1)设AD=x,则DM= . ∵矩形DMNC 与矩形ABCD 相似,
∴x 2=32.
∴x=4 或x=-4 (舍去),即AD 的长为4 .
(2)矩形DMNC 与矩形ABCD 的相似比为
例3 如图,把矩形ABCD 对折,折痕为MN,矩形DMNC 与
矩形ABCD 相似,已知AB=4.
(1)求AD 的长;
(2)求矩形DMNC 与矩形ABCD 的相似比.
探索新知
总 结
利用相似多边形的性质求线段长及相似比的方法:
先找出与已知边、未知边相关的四条对应线段,再通过设未知数并用含未知数的式子表示其中的部分线段,最后通过相似多边形的对应边成比例建立方程进行计算.这种巧用方程思想的方法在相似多边形的计算中经常运用.
典题精讲
如果两个相似多边形的一组对应边长分别为3 cm和2 cm,
那么它们的相似比是( )
A. B. C. D.
C
六边形ABCDEF 与六边形A′B′C′D′E′F ′相似,若对应边AB 与A′B ′的长分别为50 cm和40 cm,则六边形A′B′C′D′E′F ′与六边形ABCDEF 的相似比是( )
A.5:4 B.4:5
C.5:2 D.2:
2
B
易错提醒
一位同学经过研究发现:在等边三角形中,每条边都是相等的,两个等边三角形相似;在正方形中,每条边都是相等的,两个正方形相似.于是他进一步推广,认为如果多边形的各边都相等,那么这样的两个边数相同的多边形相似.你认为这种说法正确吗?为什么?
易错提醒
解:
这种说法不正确.比如,如图所示的两个菱形,每个菱形的边长都是相等的,但它们的各角并不是对应相等的,所以它们不相似.
易错点:对相似多边形定义理解不透而致错.
学以致用
小试牛刀
1 下列四组图形中,一定相似的是( )
A.正方形与矩形
B.正方形与菱形
C.菱形与菱形
D.正五边形与正五边形
D
小试牛刀
两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,
每组中的一个图形在另一个图形的内部,对应边平行,且对应边
之间的距离都相等,那么两个图形不相似的一组是( )
B
小试牛刀
志远要在报纸上刊登广告,一块10 cm×5 cm的长方形版面要付广告费180元,他要把该版面的边长都扩大为原来的3倍,在每平方厘米版面广告费相同的情况下,他该付广告费( )
A.540元 B.1 080元
C.1 620元 D.1 800元
3
C
小试牛刀
4 如图,四边形ABCD 与四边形EFGH 相似,∠A=62°,∠B=70°,∠H=140°,AD=18,EF=15,FG=14,EH=12,求∠G 的度数及AB,BC 的长.
小试牛刀
解:
∵四边形ABCD 与四边形EFGH 相似,
∴∠E=∠A=62°,∠F=∠B=70°,
又∵∠H=140°,∠E+∠F+∠G+∠H=360°,
∴∠G=88°.
∵四边形ABCD 与四边形EFGH 相似,
∴ .
又∵AD=18,EF=15,FG=14,EH=12,
∴AB=22.5,BC=21.
小试牛刀
5 如图,多边形ABCDEF 与多边形A1B1C1D1E1F1相似,其中,A,B,C,D,E,F 的对应点分别为A1,B1,C1,D1,E1,F1,∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F 的度数;
(2)如果多边形ABCDEF 和多
边形A1B1C1D1E1F1的相似比是1∶1.5,
且CD=15 cm,求C1D1的长度.
小试牛刀
(1)∵多边形ABCDEF 和多边形A1B1C1D1E1F1 相似,且∠C
和∠C1,∠D 和∠D1,∠E 和∠E1是对应角,
∴∠C=95°,∠D=135°,∠E=120°.
由多边形内角和定理,知∠F=720°-(135°+120°+ 95°+135°+120°)=115°.
解:
(2) ∵多边形ABCDEF 和多边形A1B1C1D1E1F 1的相似比
是1∶1.5,且CD=15 cm,
∴C1D1=15×1.5=22.5(cm).
小试牛刀
6 如图,将一张长、宽之比为 ∶1的矩形纸ABCD 依次不断对折,可以得到矩形BCFE,AEML,GMFH,LGPN.
(1)判断矩形ABCD,BCFE,AEML,GMFH,LGPN 的长、宽之比是否相等,并说明理由;
(2)你认为这些大小不同的矩形相似吗?
小试牛刀
解:
(1)矩形ABCD,BCFE,AEML,GMFH,LGPN 的长、宽之比相等.理由如下:
设矩形纸的宽BC=a,长AB= a,
则有BE= a,AE= a,ME= ,MF= ,
HF= a,LG= a,LN= ,
∴
小试牛刀
∴五个矩形的长、宽之比相等.
(2)这些大小不同的矩形都相似.
小试牛刀
7 一个用钢筋焊接的三角形的三边长分别是20 cm,60 cm,50 cm,现要做一个与其相似的钢筋三角形.因为只有长为30 cm和50 cm的两根钢筋,所以要求以其中一根为一边,从另一根上截下两段(允许有余料)作为另外两边,问:有几种截法?请指出用余料最少的截法截出的三边长分别为多少.
小试牛刀
解:
若截30 cm长的钢筋,设截成的两段长分别为a cm和b cm
(a<b),则有 ,解得a= ,b= .
∵a+b= + = >30,
∴此截法不成立.
若截50 cm长的钢筋,设截成的两段长分别为x cm和y cm
(x<y ),则有① ,解得x=12,y=36.
∵x+y=12+36=48<50,∴此截法成立.
小试牛刀
② ,解得x=10,y=25.
∵x+y=10+25=35<50,∴此截法成立.
因此有两种截法.
∵50-48=2(cm),50-35=15(cm),
∴用余料最少的截法截出的三边长分别为12 cm,30 cm,36 cm.
课堂小结
课堂小结
相似相似形的性质:
(1)对应角 ;
(2)对应边的比等于 ;
相等
相似比
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
