【班海精品】人教版(新)九下-27.2 相似三角形 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-27.2 相似三角形 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览








文档简介
(共39张PPT)
27.2 相似三角形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
新课精讲
探索新知
1
知识点
平行线判定三角形相似定理
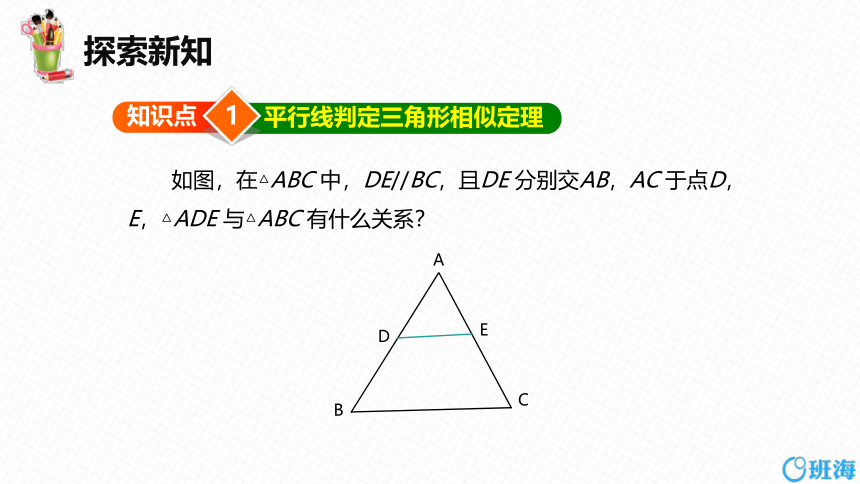
如图,在△ABC 中,DE//BC,且DE 分别交AB,AC 于点D,E,△ADE 与△ABC 有什么关系?
A
D
E
C
B
探索新知
解析:直觉告诉我们,△ADE 与△ABC 相似,我们通过相似的
定义证明它,即证明∠A=∠A,∠ADE=∠B,∠AED =∠C,
由前面的结论可得, 而 中的DE
不在△ABC 的边BC 上,不能直接利用前面的结论.但从要
证的 可以看出,除DE 外,AE,AC,BC 都在△ABC
的边上,因此只需将DE 平移到BC 边上去,使得BF=DE,再
证明 就可以了(如图).只要过点E 作EF//AB,交BC 于
点F,BF 就是平移DE 所得的线段.
探索新知
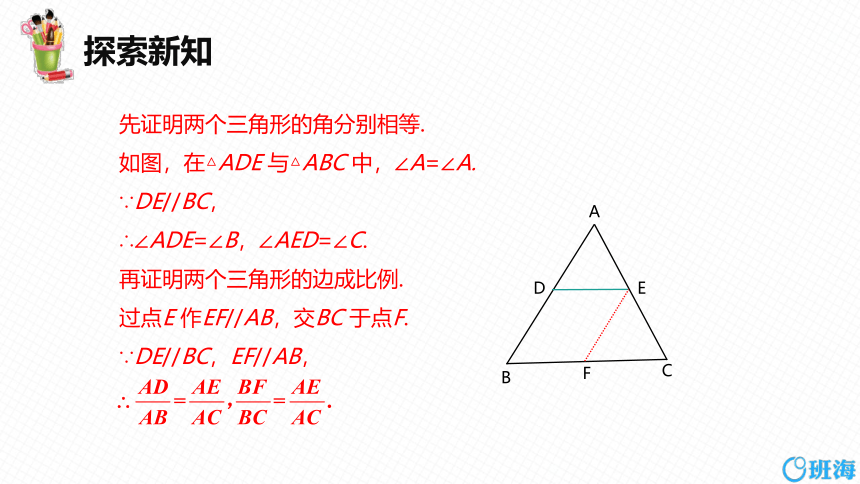
先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠A=∠A.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E 作EF//AB,交BC 于点F.
∵DE//BC,EF//AB,
A
D
E
C
B
F
探索新知
∵四边形DBFE 是平行四边形,
∴DE=BF.
这样,我们证明了△ADE 和△ABC 的角分别相等,边成比例,所以 △ADE∽△ABC.因此,我们有如下判定三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
探索新知
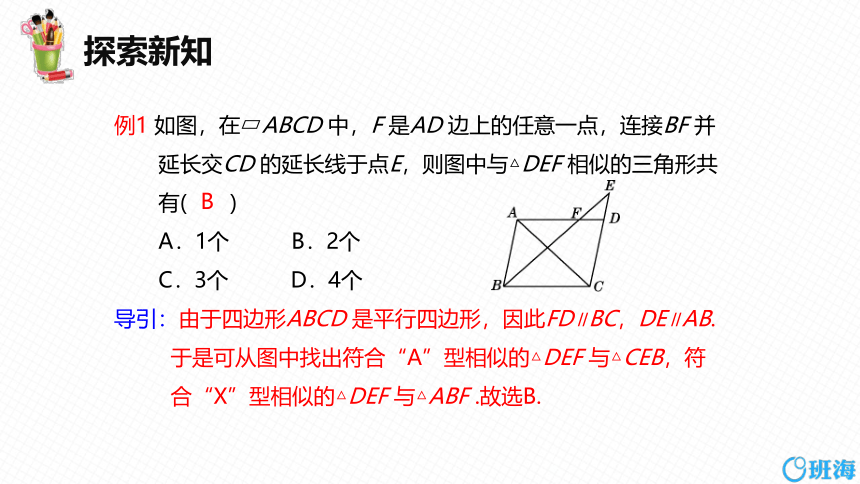
例1 如图,在 ABCD 中,F 是AD 边上的任意一点,连接BF 并延长交CD 的延长线于点E,则图中与△DEF 相似的三角形共有( )
A.1个 B.2个
C.3个 D.4个
导引:由于四边形ABCD 是平行四边形,因此FD∥BC,DE∥AB. 于是可从图中找出符合“A”型相似的△DEF 与△CEB,符合“X”型相似的△DEF 与△ABF .故选B.
B
探索新知
利用平行线寻找相似三角形的方法:
在线段较多的图形中寻找相似三角形,如果图中有线段平行的条件,则集中精力在图形中寻找符合“A”型或“X”型的基本图形,这不但是解本题的首要之选,也是今后解本类题目的首要之选.
总 结
探索新知
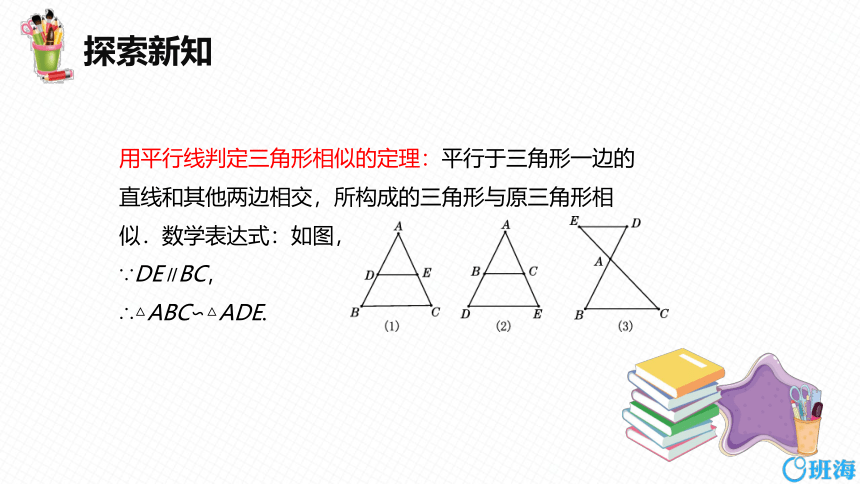
用平行线判定三角形相似的定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.数学表达式:如图,
∵DE∥BC,
∴△ABC∽△ADE.
典题精讲
如图,在△ABC 中,DE∥BC,且AD =3,DB =2.写出图中的相似三角形,并指出其相似比.
解:∵DE∥BC,
∴△ADE∽△ABC.
∴其相似比为
A
D
E
C
B
典题精讲
如图,在△ABC 中,点D,E 分别是AB,AC 的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③ . 其中正确的有( )
A.3个
B.2个
C.1个
D.0个
2
A
典题精讲
如图,AB∥CD∥EF,则图中相似三角形有( )
A.0对
B.1对
C.2对
D.3对
3
D
探索新知
2
知识点
相似三角形性质的应用
如图所示,要测量一个池塘的长是多少,不能直接测量距离,小明做了△ABC,取池塘的两个点D,E,使DE∥BC,测出BC,AD,AB 的长就可以算出DE 的长,你知道为什么吗?
原来由DE∥BC 可以得到△ABC∽△ADE,所以
AD∶AB=DE∶BC.
探索新知
归 纳
通过建立相似三角形数学模型可以解决实际问题.
探索新知
例2 如图,在 ABCD 中,AE=EB,AF=2,则FC 等于________.
导引:有平行四边形,就提供了平行线,就有三角形相似,
就有对应边的比相等,就能求出FC 的长.
在 ABCD 中,∵AB∥CD,AB=CD,
∴△AEF∽△CDF.
∵AE=EB,∴AE= AB= CD.
∴CF=2AF=4.
4
探索新知
总 结
利用证三角形相似求线段的长的方法:
当三角形被平行线所截形成“A”型或“X”型的图形,并且所求的线段或已知线段在平行的边上,通常考虑通过证三角形相似,再利用相似三角形的对应边的比相等构建包含已知与未知线段的比例式,即可求出线段的长.
典题精讲
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,
则井深为( )
A.1.25尺 B.57.5尺
C.6.25尺 D.56.5尺
1
B
典题精讲
如图,在△ABC 中,D,E 分别为AB,AC 边上的点,DE∥BC,点F 为BC 边上一点,连接AF 交DE 于点G,则下列结论中一定正确的是( )
A.
B.
C.
D.
2
C
典题精讲
如图,在△ABC 中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE 的长为( )
A.6
B.8
C.10
D.12
3
C
易错提醒
如图所示,△AOB∽△COD,下列各式中正确的有( )
A
易错点:对相似三角形的对应关系理解模糊而出错.
A.1个 B.2个 C.3个 D.4个
学以致用
小试牛刀
如图,点F 在平行四边形ABCD 的边AB上,射线CF 交DA 的延长线于点E.在不添加辅助线的情况下,与△AEF 相似的三角形有( )
A.0个
B.1个
C.2个
D.3个
1
C
小试牛刀
如图,在平行四边形ABCD 中,过点B 的直线与对角线AC、边AD 分别交于点E 和点F,过点E 作EG∥BC,交AB 于点G,则图中的相似三角形有( )
A.4对
B.5对
C.6对
D.7对
2
B
小试牛刀
如图, ABCD 的对角线AC,BD交 于点O,CE 平分∠BCD交AB 于点E,交BD 于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S ABCD=AC·BC;③OE:AC= :6;
④S△OCF=2S△OEF,其中成立的有( )
A.1个 B.2个
C.3个 D.4个
3
D
小试牛刀
4 如图,在 ABCD 中,M,N 为对角线BD 的三等分点,连接AM 并延长交BC 于点E,连接EN 并延长交AD 于点F.
(1)求证:△AMD∽△EMB;
(2)求 的值.
(1)证明:∵四边形ABCD 为平行四边形,
∴AD∥BE.∴△AMD∽△EMB.
小试牛刀
(2) ∵AD∥BC,∴△FND∽△ENB.
∴
∵M,N 为BD 的三等分点,∴
∴
解:
小试牛刀
5 如图,在 ABCD 中,点E 在边BC 上,点F 在边AD 的延长线上,且DF=BE.EF 与CD 交于点G.
(1)求证:BD∥EF;
(2)若 ,BE=4,求EC 的长.
(1)证明:∵四边形ABCD 是平行四边形,
∴AD∥BC.
∵DF=BE,
∴四边形BEFD 是平行四边形,
∴BD∥EF.
小试牛刀
(2) ∵BE=4,∴DF=4.
∵DF∥EC,
∴△DFG∽△CEG,∴
∴EC=
解:
小试牛刀
6 如图,△ABC 为锐角三角形,AD 是BC 边上的高,正方形EFGH 的一边FG 在BC 上,顶点E,H 分别在AB,AC上,已知BC=40 cm,AD=30 cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
(1)证明: ∵四边形EFGH 是正方形,
∴EH∥BC.
∴△AEH∽△ABC.
(2)如图,设AD 与EH 交于点M.
∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM 是矩形.
∴EF=DM.设正方形EFGH 的边长为x,
∵△AEH∽△ABC,∴
同理△AEM∽△ABD,
∴ ∴
∴ ,∴x=
∴正方形EFGH 的边长为 cm,面积为 cm2.
小试牛刀
解:
小试牛刀
7 如图所示,在四边形OABC 中,D,E,F 分别是OA,OB,OC上的点,连接DE,EF,DF,AC,若∠OED=∠OBA,∠OEF=∠OBC.
(1)求证:
(2)请你探究:如果△DEF 是以DF 为底边的等腰三角形,
则△ABC 是否是以AC 为底边的等腰三角形,为什么
小试牛刀
证明:
(1)求证:
∵∠OED=∠OBA,∠OEF=∠OBC,
∴DE∥AB,EF∥BC.
由DE∥AB,得△ODE∽△OAB,
∴
由EF∥BC,得△OFE∽△OCB,
∴ ∴
小试牛刀
解:
(2)请你探究:如果△DEF 是以DF 为底边的等腰三角形,
则△ABC 是否是以AC 为底边的等腰三角形,为什么
是.
理由如下:由△OFE∽△OCB,得
由△ODE∽△OAB,得
∴
∵△DEF 是以DF 为底边的等腰三角形,∴DE=EF,
∴AB=BC,即△ABC 是以AC 为底边的等腰三角形.
课堂小结
课堂小结
确定相似三角形的对应边和对应角的方法:
(1)有公共角的,公共角一般是对应角;
(2)有对顶角的,对顶角一般是对应角;
(3)相似三角形对应角所对的边是对应边,两个对
应角所夹的边是对应边;
(4)相似三角形对应边所对的角是对应角,两条对
应边所夹的角是对应角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.2 相似三角形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
新课精讲
探索新知
1
知识点
平行线判定三角形相似定理
如图,在△ABC 中,DE//BC,且DE 分别交AB,AC 于点D,E,△ADE 与△ABC 有什么关系?
A
D
E
C
B
探索新知
解析:直觉告诉我们,△ADE 与△ABC 相似,我们通过相似的
定义证明它,即证明∠A=∠A,∠ADE=∠B,∠AED =∠C,
由前面的结论可得, 而 中的DE
不在△ABC 的边BC 上,不能直接利用前面的结论.但从要
证的 可以看出,除DE 外,AE,AC,BC 都在△ABC
的边上,因此只需将DE 平移到BC 边上去,使得BF=DE,再
证明 就可以了(如图).只要过点E 作EF//AB,交BC 于
点F,BF 就是平移DE 所得的线段.
探索新知
先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠A=∠A.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E 作EF//AB,交BC 于点F.
∵DE//BC,EF//AB,
A
D
E
C
B
F
探索新知
∵四边形DBFE 是平行四边形,
∴DE=BF.
这样,我们证明了△ADE 和△ABC 的角分别相等,边成比例,所以 △ADE∽△ABC.因此,我们有如下判定三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
探索新知
例1 如图,在 ABCD 中,F 是AD 边上的任意一点,连接BF 并延长交CD 的延长线于点E,则图中与△DEF 相似的三角形共有( )
A.1个 B.2个
C.3个 D.4个
导引:由于四边形ABCD 是平行四边形,因此FD∥BC,DE∥AB. 于是可从图中找出符合“A”型相似的△DEF 与△CEB,符合“X”型相似的△DEF 与△ABF .故选B.
B
探索新知
利用平行线寻找相似三角形的方法:
在线段较多的图形中寻找相似三角形,如果图中有线段平行的条件,则集中精力在图形中寻找符合“A”型或“X”型的基本图形,这不但是解本题的首要之选,也是今后解本类题目的首要之选.
总 结
探索新知
用平行线判定三角形相似的定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.数学表达式:如图,
∵DE∥BC,
∴△ABC∽△ADE.
典题精讲
如图,在△ABC 中,DE∥BC,且AD =3,DB =2.写出图中的相似三角形,并指出其相似比.
解:∵DE∥BC,
∴△ADE∽△ABC.
∴其相似比为
A
D
E
C
B
典题精讲
如图,在△ABC 中,点D,E 分别是AB,AC 的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③ . 其中正确的有( )
A.3个
B.2个
C.1个
D.0个
2
A
典题精讲
如图,AB∥CD∥EF,则图中相似三角形有( )
A.0对
B.1对
C.2对
D.3对
3
D
探索新知
2
知识点
相似三角形性质的应用
如图所示,要测量一个池塘的长是多少,不能直接测量距离,小明做了△ABC,取池塘的两个点D,E,使DE∥BC,测出BC,AD,AB 的长就可以算出DE 的长,你知道为什么吗?
原来由DE∥BC 可以得到△ABC∽△ADE,所以
AD∶AB=DE∶BC.
探索新知
归 纳
通过建立相似三角形数学模型可以解决实际问题.
探索新知
例2 如图,在 ABCD 中,AE=EB,AF=2,则FC 等于________.
导引:有平行四边形,就提供了平行线,就有三角形相似,
就有对应边的比相等,就能求出FC 的长.
在 ABCD 中,∵AB∥CD,AB=CD,
∴△AEF∽△CDF.
∵AE=EB,∴AE= AB= CD.
∴CF=2AF=4.
4
探索新知
总 结
利用证三角形相似求线段的长的方法:
当三角形被平行线所截形成“A”型或“X”型的图形,并且所求的线段或已知线段在平行的边上,通常考虑通过证三角形相似,再利用相似三角形的对应边的比相等构建包含已知与未知线段的比例式,即可求出线段的长.
典题精讲
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,
则井深为( )
A.1.25尺 B.57.5尺
C.6.25尺 D.56.5尺
1
B
典题精讲
如图,在△ABC 中,D,E 分别为AB,AC 边上的点,DE∥BC,点F 为BC 边上一点,连接AF 交DE 于点G,则下列结论中一定正确的是( )
A.
B.
C.
D.
2
C
典题精讲
如图,在△ABC 中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE 的长为( )
A.6
B.8
C.10
D.12
3
C
易错提醒
如图所示,△AOB∽△COD,下列各式中正确的有( )
A
易错点:对相似三角形的对应关系理解模糊而出错.
A.1个 B.2个 C.3个 D.4个
学以致用
小试牛刀
如图,点F 在平行四边形ABCD 的边AB上,射线CF 交DA 的延长线于点E.在不添加辅助线的情况下,与△AEF 相似的三角形有( )
A.0个
B.1个
C.2个
D.3个
1
C
小试牛刀
如图,在平行四边形ABCD 中,过点B 的直线与对角线AC、边AD 分别交于点E 和点F,过点E 作EG∥BC,交AB 于点G,则图中的相似三角形有( )
A.4对
B.5对
C.6对
D.7对
2
B
小试牛刀
如图, ABCD 的对角线AC,BD交 于点O,CE 平分∠BCD交AB 于点E,交BD 于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S ABCD=AC·BC;③OE:AC= :6;
④S△OCF=2S△OEF,其中成立的有( )
A.1个 B.2个
C.3个 D.4个
3
D
小试牛刀
4 如图,在 ABCD 中,M,N 为对角线BD 的三等分点,连接AM 并延长交BC 于点E,连接EN 并延长交AD 于点F.
(1)求证:△AMD∽△EMB;
(2)求 的值.
(1)证明:∵四边形ABCD 为平行四边形,
∴AD∥BE.∴△AMD∽△EMB.
小试牛刀
(2) ∵AD∥BC,∴△FND∽△ENB.
∴
∵M,N 为BD 的三等分点,∴
∴
解:
小试牛刀
5 如图,在 ABCD 中,点E 在边BC 上,点F 在边AD 的延长线上,且DF=BE.EF 与CD 交于点G.
(1)求证:BD∥EF;
(2)若 ,BE=4,求EC 的长.
(1)证明:∵四边形ABCD 是平行四边形,
∴AD∥BC.
∵DF=BE,
∴四边形BEFD 是平行四边形,
∴BD∥EF.
小试牛刀
(2) ∵BE=4,∴DF=4.
∵DF∥EC,
∴△DFG∽△CEG,∴
∴EC=
解:
小试牛刀
6 如图,△ABC 为锐角三角形,AD 是BC 边上的高,正方形EFGH 的一边FG 在BC 上,顶点E,H 分别在AB,AC上,已知BC=40 cm,AD=30 cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
(1)证明: ∵四边形EFGH 是正方形,
∴EH∥BC.
∴△AEH∽△ABC.
(2)如图,设AD 与EH 交于点M.
∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM 是矩形.
∴EF=DM.设正方形EFGH 的边长为x,
∵△AEH∽△ABC,∴
同理△AEM∽△ABD,
∴ ∴
∴ ,∴x=
∴正方形EFGH 的边长为 cm,面积为 cm2.
小试牛刀
解:
小试牛刀
7 如图所示,在四边形OABC 中,D,E,F 分别是OA,OB,OC上的点,连接DE,EF,DF,AC,若∠OED=∠OBA,∠OEF=∠OBC.
(1)求证:
(2)请你探究:如果△DEF 是以DF 为底边的等腰三角形,
则△ABC 是否是以AC 为底边的等腰三角形,为什么
小试牛刀
证明:
(1)求证:
∵∠OED=∠OBA,∠OEF=∠OBC,
∴DE∥AB,EF∥BC.
由DE∥AB,得△ODE∽△OAB,
∴
由EF∥BC,得△OFE∽△OCB,
∴ ∴
小试牛刀
解:
(2)请你探究:如果△DEF 是以DF 为底边的等腰三角形,
则△ABC 是否是以AC 为底边的等腰三角形,为什么
是.
理由如下:由△OFE∽△OCB,得
由△ODE∽△OAB,得
∴
∵△DEF 是以DF 为底边的等腰三角形,∴DE=EF,
∴AB=BC,即△ABC 是以AC 为底边的等腰三角形.
课堂小结
课堂小结
确定相似三角形的对应边和对应角的方法:
(1)有公共角的,公共角一般是对应角;
(2)有对顶角的,对顶角一般是对应角;
(3)相似三角形对应角所对的边是对应边,两个对
应角所夹的边是对应边;
(4)相似三角形对应边所对的角是对应角,两条对
应边所夹的角是对应角.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
