【班海精品】人教版(新)九下-27.1 图形的相似 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】人教版(新)九下-27.1 图形的相似 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 10:06:33 | ||
图片预览









文档简介
(共47张PPT)
27.1 图形的相似
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
全等图形
指能够完全重合的两个图形,即它们的形状和大小完全相同.
回忆
新课精讲
探索新知
1
知识点
相似图形
问题:每组图片中的两张图片有何关系?
探索新知
想一想:我们刚才所见到的图形有什么相同和不同的地方
相同点:形状相同.
不同点:大小不一定相同.
生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为:
相似形
探索新知
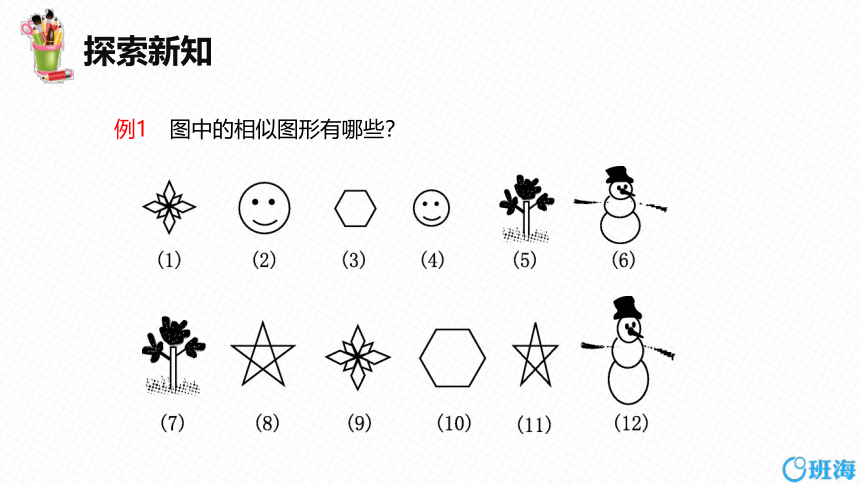
例1 图中的相似图形有哪些?
探索新知
本题依据相似图形的定义求解.观察这些图形,虽然图(6)与图(12)、图(8)与图(11)极为相似,但是它们的形状不相同.图(6)“拉长”而不是整体放大变成了图(12),图(8)“压缩”而不是整体缩小变成了图(11),所以它们不是相似图形.而图(1)与图(9)、图(2)与图(4)、图(3)与图(10)、图(5)与图(7)的形状完全相同,所以它们是相似图形.
导引:
解:相似图形有:图(1)和图(9),图(2)和图(4),图(3)和图(10),
图(5)和图(7).
探索新知
总 结
(1)两个图形相似是指它们的形状相同,与它们的位置无关;
(2)全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.
典题精讲
1 如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
解:相似.
典题精讲
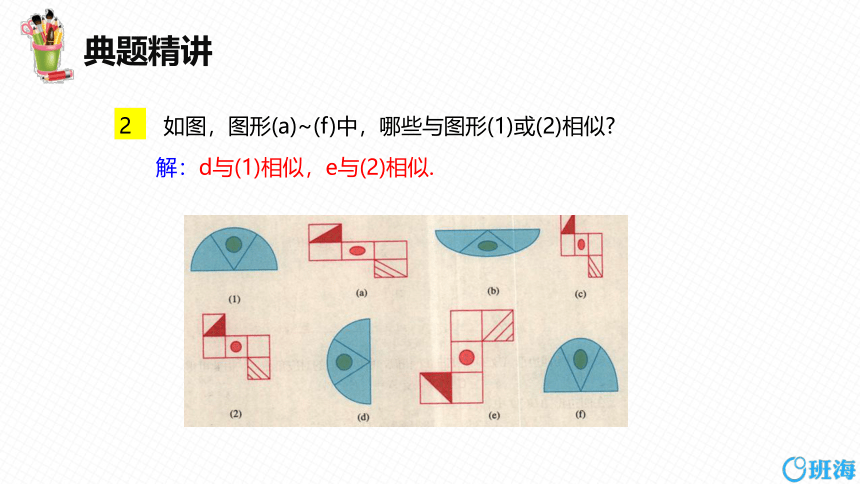
2 如图,图形(a)~(f)中,哪些与图形(1)或(2)相似
解:d与(1)相似,e与(2)相似.
典题精讲
3 下列说法中,不正确的是( )
A.同一版的8开中国地图与32开中国地图相似
B.亮亮4岁时的照片与16岁时的照片相似
C.用放大镜看到的图形与原图形相似
D.所有的圆都相似
B
探索新知
2
知识点
两条线段的比
绳子的出现最早可以追溯到数万年前.在人类开始有最简单工具的时候,他们会用草或细小的树枝绞合搓捻成绳子.不通过测量,运用所学知识,快速地把一长为 50cm 的细线分成两部分,使两部分之比为 2︰3 ,该如何分?
探索新知
两条线段的比:在同一单位长度下,两条线段长度的比值叫做两条线段的比.
例2 若a=0.2 m,b=8 cm,则a∶b=________.
a=0.2 m=20 cm,a∶b=20∶8=5∶2.
5∶2
导引:
探索新知
总 结
求线段的长度比,先看单位是否统一,不统一的要化为同一单位,再把数值进行化简化成最简整数比.
典题精讲
在比例尺为1:10 000 000的地图上,量的甲乙两地的距离是30cm,求两地的实际距离.
3000km.
解:
在1 : 1 000 000的地图上,A,B两点之间的距离是5 cm,则A,B两地的实际距离是( )
A.5 km B.50 km
C.500 km D.5 000 km
B
探索新知
在四条线段 a、b、c、d 中,如果 a 和 b 的比等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例线段, 简称比例线段.
外项
外项
内项
内项
a :b = c :d
外项
内项
a、b、c 的第四比例项
成比例线段:
3
知识点
成比例线段
探索新知
如果作为比例内项的是两条相等的线段即
或a :b = b :c,
那么线段 b 叫做线段 a 和 c 的比例中项.
探索新知
例3 下列各组线段中,能成比例线段的是( )
A.1 cm,3 cm ,4 cm ,6 cm
B.30 cm ,12 cm ,0.8 cm ,0.2 cm
C.0.1 cm ,0.2 cm ,0.3 cm ,0.4 cm
D.12 cm ,16 cm ,45 cm ,60 cm
从比例线段的概念入手.作为选择题,可逐个排查.为了能迅
速找到比例关系,可首先对数据按大小排序,以减少试验
的次数.A中的 ,它们不成比例;B中的 ,它
们不成比例;C中的 ,它们不成比例;D中的 ,
它们成比例.故选D.
D
分析:
探索新知
总 结
判断线段是否成比例,其基本方法是先排序,后求比值,再看比值是否相等.
典题精讲
下列四组线段中,是成比例线段的是( )
A.3 cm,4 cm,5 cm,6 cm
B.4 cm,8 cm,3 cm,5 cm
C.5 cm,15 cm,2 cm,6 cm
D.8 cm,4 cm,1 cm,3 cm
1
C
四条线段a,b,c,d 成比例(即 ),其中a=3 cm,d=4 cm,c=6 cm,则b 等于( )
A.8 cm B. cm
C. cm D.2 cm
D
典题精讲
已知线段a=4,b=16,线段c 是线段a,b 的比
例中项(即 ),那么c 等于( )
A.10 B.8
C.-8 D.±8
B
矩形的两边长分别为a,b,下列数据能构成黄金矩形的是( )
A.a=4,b= +2
B.a=4,b= -2
C.a=2,b= +1
D.a=2,b= -1
D
探索新知
4
知识点
比例的性质
比例的基本性质:
(1)如果 ,那么
等积式
比例式
内项积=外项积
探索新知
(2)如果 ,且
那么
探索新知
总 结
比例的基本性质常用于比例式与乘积式的互相转化,关键是把握两内项之积等于两外项之积.
探索新知
分析:从比例线段的性质入手.根据比例的基本性质把5x-4y=0
变形为: ,然后利用合比性质变形即得.也可使用
“设参数”的方式,代入后约分即可.
解:∵ 5x-4y =0 ,∴ .∴
令x =4k,y =5k ,则
例4 若5x-4y=0,则 =____; =____;
=____; =____;
探索新知
总 结
利用比例的性质求代数式值的方法:当一个题中出现多个未知数时,常巧用“消元法”求代数式的值;当条件中出现多个比值相等时,用“中间量法”巧设出比值是首选的方法.
典题精讲
已知2x=3y ( y≠0),则下面结论成立的是( )
A. B.
C. D.
A
2 若 ,则 的值为( )
A.1 B. C. D.
D
典题精讲
若x:y=1:3,2y=3z,则 的值是( )
A.-5 B. C. D.5
A
如果 (b+d+f ≠0),且a+c+e=3(b+d+f ),
那么k=________.
3
易错提醒
已知线段a=3,b=5,c=7,则a,b,c 的第四比例项x=________.
易错点:忽视线段成比例的顺序性.
易错总结:要求a,b,c 的第四比例项x,就有a∶b=c∶x,所以
x= ,切勿看到线段成比例就分类讨论,从而造成错误.
学以致用
小试牛刀
1 某机器零件在图纸上的长度是21 mm,它的实际长度是
630 mm,则图纸的比例尺是( )
A.1∶20 B.1∶30 C.1∶40 D.1∶50
2 已知线段AB,在BA 的延长线上取一点C,使CA=3AB,
则线段CA 与线段CB 的长度比为( )
A.3∶4 B.2∶3 C.3∶5 D.1∶2
B
A
小试牛刀
3 下列和如图所示的图形形状相同的是( )
A
小试牛刀
4 如图,在△ABC 中,AB=24,AE=6,EC=10,
(1)求AD 的长;
(2)试说明
小试牛刀
解:
(1)设AD=x,则BD=24-x,
由 得 ,
解得x=9. ∴AD=9.
(2)由AB=24,AD=9得BD=15,
∵
∴
小试牛刀
5 已知线段a,b,c 满足 ≠0,且a+2b+c=26
(1)求线段a,b,c 的长;
(2)若线段x 是线段a,b 的比例中项,求x.
小试牛刀
(1)设 =k (k≠0),∴a=3k,b=2k,c=6k.
∵a+2b+c=26,∴3k+4k+6k=26,即k=2.
∴a=6,b=4,c=12.
解:
(2)∵线段x 是线段a,b 的比例中项,
∴x 2=ab.
又∵a=6,b=4,∴x=2 (负值舍去).
小试牛刀
6 已知a,b,c 是△ABC 的三边长,且 ≠0,
(1)求 的值;
(2)若△ABC 的周长为90,求各边的长.
小试牛刀
解:
(2)因为△ABC 的周长为90,所以a+b+c=90,
即5k+4k+6k=90. 解得k=6,
所以a=30,b=24,c=36.
(1)设 (k≠0),
则a=5k,b=4k,c=6k,
所以
小试牛刀
7 如图,在Rt△ABC 中,CD 是斜边AB上的高,试猜想线段AB,AC,BC,CD是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不成比例,请说明理由.
小试牛刀
解:
线段AB,AC,BC,CD 对应成比例,且
验证如下:根据三角形的面积公式,得
AB CD= AC BC,
∴AB CD=AC BC,即
小试牛刀
8 设a,b,c 是△ABC 的三边长,且
判断△ABC 为何种三角形,并说明理由.
解:
△ABC 为等边三角形.理由如下:
∵a,b,c 是△ABC 的三边长,∴a+b+c ≠0.
∵
∴
∴a=b=c. ∴△ABC 为等边三角形.
小试牛刀
9 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC 的中点E,F,连接EF;以点F 为圆心,以FD 为半径画弧,交BC 的延长线于点G;作GH⊥AD,交AD 的延长线于点H,则下列矩形是黄金矩形的是( )
A.矩形ABFE
B.矩形EFCD
C.矩形EFGH
D.矩形DCGH
D
课堂小结
课堂小结
相似图形的定义;
判断是否是成比例线段:
一排(排顺序)、二算(算比值或乘积、三判断;
3. 比例的基本性质: ad=bc;
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
27.1 图形的相似
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
全等图形
指能够完全重合的两个图形,即它们的形状和大小完全相同.
回忆
新课精讲
探索新知
1
知识点
相似图形
问题:每组图片中的两张图片有何关系?
探索新知
想一想:我们刚才所见到的图形有什么相同和不同的地方
相同点:形状相同.
不同点:大小不一定相同.
生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为:
相似形
探索新知
例1 图中的相似图形有哪些?
探索新知
本题依据相似图形的定义求解.观察这些图形,虽然图(6)与图(12)、图(8)与图(11)极为相似,但是它们的形状不相同.图(6)“拉长”而不是整体放大变成了图(12),图(8)“压缩”而不是整体缩小变成了图(11),所以它们不是相似图形.而图(1)与图(9)、图(2)与图(4)、图(3)与图(10)、图(5)与图(7)的形状完全相同,所以它们是相似图形.
导引:
解:相似图形有:图(1)和图(9),图(2)和图(4),图(3)和图(10),
图(5)和图(7).
探索新知
总 结
(1)两个图形相似是指它们的形状相同,与它们的位置无关;
(2)全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.
典题精讲
1 如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
解:相似.
典题精讲
2 如图,图形(a)~(f)中,哪些与图形(1)或(2)相似
解:d与(1)相似,e与(2)相似.
典题精讲
3 下列说法中,不正确的是( )
A.同一版的8开中国地图与32开中国地图相似
B.亮亮4岁时的照片与16岁时的照片相似
C.用放大镜看到的图形与原图形相似
D.所有的圆都相似
B
探索新知
2
知识点
两条线段的比
绳子的出现最早可以追溯到数万年前.在人类开始有最简单工具的时候,他们会用草或细小的树枝绞合搓捻成绳子.不通过测量,运用所学知识,快速地把一长为 50cm 的细线分成两部分,使两部分之比为 2︰3 ,该如何分?
探索新知
两条线段的比:在同一单位长度下,两条线段长度的比值叫做两条线段的比.
例2 若a=0.2 m,b=8 cm,则a∶b=________.
a=0.2 m=20 cm,a∶b=20∶8=5∶2.
5∶2
导引:
探索新知
总 结
求线段的长度比,先看单位是否统一,不统一的要化为同一单位,再把数值进行化简化成最简整数比.
典题精讲
在比例尺为1:10 000 000的地图上,量的甲乙两地的距离是30cm,求两地的实际距离.
3000km.
解:
在1 : 1 000 000的地图上,A,B两点之间的距离是5 cm,则A,B两地的实际距离是( )
A.5 km B.50 km
C.500 km D.5 000 km
B
探索新知
在四条线段 a、b、c、d 中,如果 a 和 b 的比等于 c 和 d 的比,那么这四条线段a、b、c、d 叫做成比例线段, 简称比例线段.
外项
外项
内项
内项
a :b = c :d
外项
内项
a、b、c 的第四比例项
成比例线段:
3
知识点
成比例线段
探索新知
如果作为比例内项的是两条相等的线段即
或a :b = b :c,
那么线段 b 叫做线段 a 和 c 的比例中项.
探索新知
例3 下列各组线段中,能成比例线段的是( )
A.1 cm,3 cm ,4 cm ,6 cm
B.30 cm ,12 cm ,0.8 cm ,0.2 cm
C.0.1 cm ,0.2 cm ,0.3 cm ,0.4 cm
D.12 cm ,16 cm ,45 cm ,60 cm
从比例线段的概念入手.作为选择题,可逐个排查.为了能迅
速找到比例关系,可首先对数据按大小排序,以减少试验
的次数.A中的 ,它们不成比例;B中的 ,它
们不成比例;C中的 ,它们不成比例;D中的 ,
它们成比例.故选D.
D
分析:
探索新知
总 结
判断线段是否成比例,其基本方法是先排序,后求比值,再看比值是否相等.
典题精讲
下列四组线段中,是成比例线段的是( )
A.3 cm,4 cm,5 cm,6 cm
B.4 cm,8 cm,3 cm,5 cm
C.5 cm,15 cm,2 cm,6 cm
D.8 cm,4 cm,1 cm,3 cm
1
C
四条线段a,b,c,d 成比例(即 ),其中a=3 cm,d=4 cm,c=6 cm,则b 等于( )
A.8 cm B. cm
C. cm D.2 cm
D
典题精讲
已知线段a=4,b=16,线段c 是线段a,b 的比
例中项(即 ),那么c 等于( )
A.10 B.8
C.-8 D.±8
B
矩形的两边长分别为a,b,下列数据能构成黄金矩形的是( )
A.a=4,b= +2
B.a=4,b= -2
C.a=2,b= +1
D.a=2,b= -1
D
探索新知
4
知识点
比例的性质
比例的基本性质:
(1)如果 ,那么
等积式
比例式
内项积=外项积
探索新知
(2)如果 ,且
那么
探索新知
总 结
比例的基本性质常用于比例式与乘积式的互相转化,关键是把握两内项之积等于两外项之积.
探索新知
分析:从比例线段的性质入手.根据比例的基本性质把5x-4y=0
变形为: ,然后利用合比性质变形即得.也可使用
“设参数”的方式,代入后约分即可.
解:∵ 5x-4y =0 ,∴ .∴
令x =4k,y =5k ,则
例4 若5x-4y=0,则 =____; =____;
=____; =____;
探索新知
总 结
利用比例的性质求代数式值的方法:当一个题中出现多个未知数时,常巧用“消元法”求代数式的值;当条件中出现多个比值相等时,用“中间量法”巧设出比值是首选的方法.
典题精讲
已知2x=3y ( y≠0),则下面结论成立的是( )
A. B.
C. D.
A
2 若 ,则 的值为( )
A.1 B. C. D.
D
典题精讲
若x:y=1:3,2y=3z,则 的值是( )
A.-5 B. C. D.5
A
如果 (b+d+f ≠0),且a+c+e=3(b+d+f ),
那么k=________.
3
易错提醒
已知线段a=3,b=5,c=7,则a,b,c 的第四比例项x=________.
易错点:忽视线段成比例的顺序性.
易错总结:要求a,b,c 的第四比例项x,就有a∶b=c∶x,所以
x= ,切勿看到线段成比例就分类讨论,从而造成错误.
学以致用
小试牛刀
1 某机器零件在图纸上的长度是21 mm,它的实际长度是
630 mm,则图纸的比例尺是( )
A.1∶20 B.1∶30 C.1∶40 D.1∶50
2 已知线段AB,在BA 的延长线上取一点C,使CA=3AB,
则线段CA 与线段CB 的长度比为( )
A.3∶4 B.2∶3 C.3∶5 D.1∶2
B
A
小试牛刀
3 下列和如图所示的图形形状相同的是( )
A
小试牛刀
4 如图,在△ABC 中,AB=24,AE=6,EC=10,
(1)求AD 的长;
(2)试说明
小试牛刀
解:
(1)设AD=x,则BD=24-x,
由 得 ,
解得x=9. ∴AD=9.
(2)由AB=24,AD=9得BD=15,
∵
∴
小试牛刀
5 已知线段a,b,c 满足 ≠0,且a+2b+c=26
(1)求线段a,b,c 的长;
(2)若线段x 是线段a,b 的比例中项,求x.
小试牛刀
(1)设 =k (k≠0),∴a=3k,b=2k,c=6k.
∵a+2b+c=26,∴3k+4k+6k=26,即k=2.
∴a=6,b=4,c=12.
解:
(2)∵线段x 是线段a,b 的比例中项,
∴x 2=ab.
又∵a=6,b=4,∴x=2 (负值舍去).
小试牛刀
6 已知a,b,c 是△ABC 的三边长,且 ≠0,
(1)求 的值;
(2)若△ABC 的周长为90,求各边的长.
小试牛刀
解:
(2)因为△ABC 的周长为90,所以a+b+c=90,
即5k+4k+6k=90. 解得k=6,
所以a=30,b=24,c=36.
(1)设 (k≠0),
则a=5k,b=4k,c=6k,
所以
小试牛刀
7 如图,在Rt△ABC 中,CD 是斜边AB上的高,试猜想线段AB,AC,BC,CD是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不成比例,请说明理由.
小试牛刀
解:
线段AB,AC,BC,CD 对应成比例,且
验证如下:根据三角形的面积公式,得
AB CD= AC BC,
∴AB CD=AC BC,即
小试牛刀
8 设a,b,c 是△ABC 的三边长,且
判断△ABC 为何种三角形,并说明理由.
解:
△ABC 为等边三角形.理由如下:
∵a,b,c 是△ABC 的三边长,∴a+b+c ≠0.
∵
∴
∴a=b=c. ∴△ABC 为等边三角形.
小试牛刀
9 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC 的中点E,F,连接EF;以点F 为圆心,以FD 为半径画弧,交BC 的延长线于点G;作GH⊥AD,交AD 的延长线于点H,则下列矩形是黄金矩形的是( )
A.矩形ABFE
B.矩形EFCD
C.矩形EFGH
D.矩形DCGH
D
课堂小结
课堂小结
相似图形的定义;
判断是否是成比例线段:
一排(排顺序)、二算(算比值或乘积、三判断;
3. 比例的基本性质: ad=bc;
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
