人教版(2019)新教材高中物理必修2 第6章 圆周运动专题 圆周运动的综合分析(共25张PPT)
文档属性
| 名称 | 人教版(2019)新教材高中物理必修2 第6章 圆周运动专题 圆周运动的综合分析(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 701.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
专题强化 圆周运动的综合分析
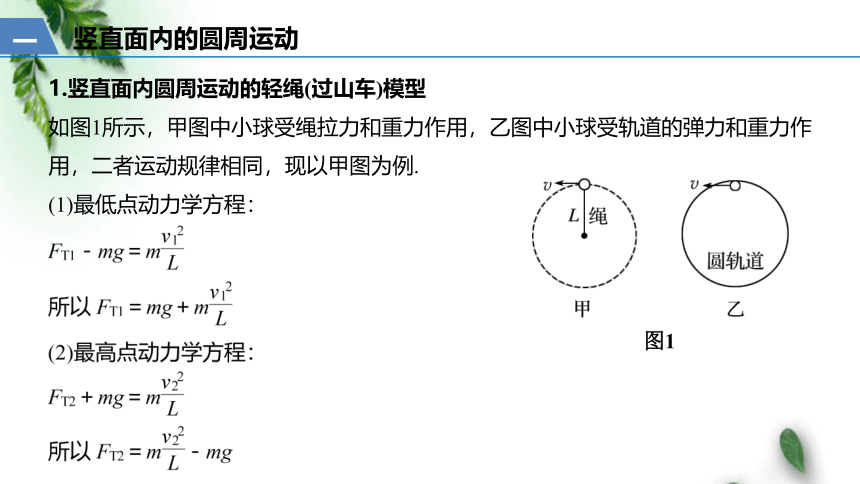
1.竖直面内圆周运动的轻绳(过山车)模型
如图1所示,甲图中小球受绳拉力和重力作用,乙图中小球受轨道的弹力和重力作用,二者运动规律相同,现以甲图为例.
(1)最低点动力学方程:
竖直面内的圆周运动
一
图1
例1 如图2所示,长度为L=0.4 m的轻绳,系一小球在竖直平面内做圆周运动,小球的质量为m=0.5 kg,小球半径不计,g取10 m/s2,求:
图2
(1)小球刚好通过最高点时的速度大小;
答案 2 m/s
(2)小球通过最高点时的速度大小为4 m/s时,绳的拉力大小;
答案 15 N
(3)若轻绳能承受的最大张力为45 N,小球运动过程中速度的最大值.
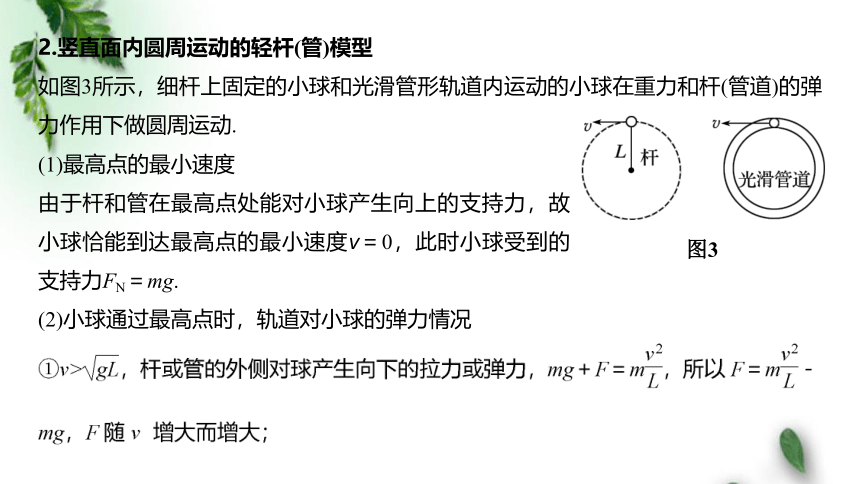
2.竖直面内圆周运动的轻杆(管)模型
如图3所示,细杆上固定的小球和光滑管形轨道内运动的小球在重力和杆(管道)的弹力作用下做圆周运动.
图3
(1)最高点的最小速度
由于杆和管在最高点处能对小球产生向上的支持力,故小球恰能到达最高点的最小速度v=0,此时小球受到的支持力FN=mg.
(2)小球通过最高点时,轨道对小球的弹力情况
例2 如图4,长为0.5 m的轻杆OA绕O点在竖直面内做圆周运动,A端连着一个质量m=2 kg的小球(半径不计).求在下述的两种情况下,通过最高点时小球对杆的作用力的大小和方向(g取10 m/s2,取π2=10):
(1)杆做匀速圆周运动的转速为2 r/s;
图4
答案 140 N 方向竖直向上
解析 假设小球在最高点受到轻杆的作用力竖直向下,则小球受力如图所示:
杆的转速为2 r/s时,ω=2π·n=4π rad/s,
由牛顿第二定律得F+mg=mLω2,
故小球所受杆的作用力
F=mLω2-mg=2×(0.5×42×π2-10) N=140 N,
即杆对小球有140 N的拉力,由牛顿第三定律可知,小球对杆的拉力大小为140 N,方向竖直向上.
(2)杆做匀速圆周运动的转速为0.5 r/s.
答案 10 N 方向竖直向下
解析 杆的转速为0.5 r/s时,ω′=2π·n′=π rad/s,
同理可得小球所受杆的作用力
F′=mLω′2-mg=2×(0.5×π2-10) N=-10 N.
力F′为负值表示它的方向与受力分析中假设的方向相反,即杆对小球有10 N的支持力,由牛顿第三定律可知,小球对杆的压力大小为10 N,方向竖直向下.
物体做圆周运动时,若物体的线速度大小、角速度发生变化,会引起某些力(如拉力、支持力、摩擦力)发生变化,进而出现某些物理量或运动状态的突变,即出现临界状态,分析圆周运动临界问题的方法是让角速度或线速度从小逐渐增大,分析各量的变化,找出临界状态.
通常碰到较多的是涉及如下三种力的作用:
(1)与绳的弹力有关的临界条件:绳弹力恰好为0.
(2)与支持面弹力有关的临界条件:支持力恰好为0.
(3)因静摩擦力而产生的临界问题:静摩擦力达到最大值.
圆周运动的临界问题
二
例3 如图5所示,用一根长为l=1 m的细线,一端系一质量为m=1 kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT.(g取10 m/s2,sin 37°=0.6,cos 37°=0.8,结果可用根式表示)
(1)若要小球离开锥面,则小球的角速度ω0至少为多大?
图5
解析 若要小球刚好离开锥面,则小球只受到重力和细线的拉力,受力分析如图所示.小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平,在水平方向运用牛顿第二定律及向心力公式得
mgtan θ=mω02lsin θ
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大?
解析 同理,当细线与竖直方向成60°角时,小球已离开锥面,由牛顿第二定律及向心力公式得mgtan α=mω′2lsin α
例4 如图6甲所示,水平转盘上放有质量为m的物块,物块到转轴的距离为r,物块和转盘间的动摩擦因数为μ,设物块受到的最大静摩擦力等于滑动摩擦力,已知重力加速度为g.
图6
(1)当水平转盘以角速度ω1匀速转动时,物块与转盘刚好能相对静止,求ω1的值;
解析 当水平转盘以角速度ω1匀速转动时,物块与转盘刚好能相对静止,则此时物块所需向心力恰好完全由最大静摩擦力提供,则μmg=mrω12
(2)如图乙,将物块和转轴用细绳相连,当转盘的角速度ω2= 时,求细绳的拉
力FT2的大小;
答案 0
解析 由于ω2<ω1,物块受到的最大静摩擦力大于所需向心力,此时绳对物块没有拉力,故FT2=0.
(3)将物块和转轴用细绳相连,当转盘的角速度ω3= 时,求细绳的拉力FT3的大小.
解析 由于ω3>ω1,物块受到的最大静摩擦力不足以提供所需的向心力,此时绳对物块有拉力,则μmg+FT3=mω32r,可得此时绳子对物块拉力的大小为FT3= μmg.
1.(轻绳模型)杂技演员表演“水流星”,在长为1.6 m的细绳的一端,系一个与水的总质量为m=0.5 kg的大小不计的盛水容器,以绳的另一端为圆心,在竖直平面内做圆周运动,如图7所示,若“水流星”通过最高点时的速率为4 m/s,则下列说法正确的是(g取10 m/s2)
A.“水流星”通过最高点时,有水从容器中流出
B.“水流星”通过最高点时,绳的张力及容器底部受到的压力均为零
C.“水流星”通过最高点时,处于完全失重状态,不受力的作用
D.“水流星”通过最高点时,绳子的拉力大小为5 N
1
2
3
4
图7
√
解析 “水流星”在最高点的临界速度v= =4 m/s,由此知绳的拉力恰好为零,且水恰好不流出,故选B.
2.(过山车模型)(多选)如图8所示,质量为m的小球在竖直平面内的光滑圆环内侧做圆周运动.圆环半径为R,小球半径不计,小球经过圆环内侧最高点时刚好不脱离圆环,则其通过最高点时下列表述正确的是
A.小球对圆环的压力大小等于mg
B.重力mg充当小球做圆周运动所需的向心力
C.小球的线速度大小等于
D.小球的向心加速度大小等于g
1
2
3
4
√
√
图8
√
1
2
3
4
解析 因为小球经过圆环内侧最高点时刚好不脱离圆环,故在最高点时小球对圆环的压力为零,选项A错误;
1
2
3
4
图9
√
1
2
3
4
4.(圆周运动的临界问题)如图10所示,A、B、C三个物体放在旋转的水平圆盘面上,物体与盘面间的最大静摩擦力均是其重力的k倍,三物体的质量分别为2m、m、m,它们离转轴的距离分别为R、R、2R.当圆盘旋转时,若A、B、C三物体均相对圆盘静止,则下列说法正确的是
A.A的向心加速度最大
B.B和C所受摩擦力大小相等
C.当圆盘转速缓慢增大时,C比A先滑动
D.当圆盘转速缓慢增大时,B比A先滑动
1
2
3
4
图10
√
专题强化 圆周运动的综合分析
1.竖直面内圆周运动的轻绳(过山车)模型
如图1所示,甲图中小球受绳拉力和重力作用,乙图中小球受轨道的弹力和重力作用,二者运动规律相同,现以甲图为例.
(1)最低点动力学方程:
竖直面内的圆周运动
一
图1
例1 如图2所示,长度为L=0.4 m的轻绳,系一小球在竖直平面内做圆周运动,小球的质量为m=0.5 kg,小球半径不计,g取10 m/s2,求:
图2
(1)小球刚好通过最高点时的速度大小;
答案 2 m/s
(2)小球通过最高点时的速度大小为4 m/s时,绳的拉力大小;
答案 15 N
(3)若轻绳能承受的最大张力为45 N,小球运动过程中速度的最大值.
2.竖直面内圆周运动的轻杆(管)模型
如图3所示,细杆上固定的小球和光滑管形轨道内运动的小球在重力和杆(管道)的弹力作用下做圆周运动.
图3
(1)最高点的最小速度
由于杆和管在最高点处能对小球产生向上的支持力,故小球恰能到达最高点的最小速度v=0,此时小球受到的支持力FN=mg.
(2)小球通过最高点时,轨道对小球的弹力情况
例2 如图4,长为0.5 m的轻杆OA绕O点在竖直面内做圆周运动,A端连着一个质量m=2 kg的小球(半径不计).求在下述的两种情况下,通过最高点时小球对杆的作用力的大小和方向(g取10 m/s2,取π2=10):
(1)杆做匀速圆周运动的转速为2 r/s;
图4
答案 140 N 方向竖直向上
解析 假设小球在最高点受到轻杆的作用力竖直向下,则小球受力如图所示:
杆的转速为2 r/s时,ω=2π·n=4π rad/s,
由牛顿第二定律得F+mg=mLω2,
故小球所受杆的作用力
F=mLω2-mg=2×(0.5×42×π2-10) N=140 N,
即杆对小球有140 N的拉力,由牛顿第三定律可知,小球对杆的拉力大小为140 N,方向竖直向上.
(2)杆做匀速圆周运动的转速为0.5 r/s.
答案 10 N 方向竖直向下
解析 杆的转速为0.5 r/s时,ω′=2π·n′=π rad/s,
同理可得小球所受杆的作用力
F′=mLω′2-mg=2×(0.5×π2-10) N=-10 N.
力F′为负值表示它的方向与受力分析中假设的方向相反,即杆对小球有10 N的支持力,由牛顿第三定律可知,小球对杆的压力大小为10 N,方向竖直向下.
物体做圆周运动时,若物体的线速度大小、角速度发生变化,会引起某些力(如拉力、支持力、摩擦力)发生变化,进而出现某些物理量或运动状态的突变,即出现临界状态,分析圆周运动临界问题的方法是让角速度或线速度从小逐渐增大,分析各量的变化,找出临界状态.
通常碰到较多的是涉及如下三种力的作用:
(1)与绳的弹力有关的临界条件:绳弹力恰好为0.
(2)与支持面弹力有关的临界条件:支持力恰好为0.
(3)因静摩擦力而产生的临界问题:静摩擦力达到最大值.
圆周运动的临界问题
二
例3 如图5所示,用一根长为l=1 m的细线,一端系一质量为m=1 kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT.(g取10 m/s2,sin 37°=0.6,cos 37°=0.8,结果可用根式表示)
(1)若要小球离开锥面,则小球的角速度ω0至少为多大?
图5
解析 若要小球刚好离开锥面,则小球只受到重力和细线的拉力,受力分析如图所示.小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平,在水平方向运用牛顿第二定律及向心力公式得
mgtan θ=mω02lsin θ
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大?
解析 同理,当细线与竖直方向成60°角时,小球已离开锥面,由牛顿第二定律及向心力公式得mgtan α=mω′2lsin α
例4 如图6甲所示,水平转盘上放有质量为m的物块,物块到转轴的距离为r,物块和转盘间的动摩擦因数为μ,设物块受到的最大静摩擦力等于滑动摩擦力,已知重力加速度为g.
图6
(1)当水平转盘以角速度ω1匀速转动时,物块与转盘刚好能相对静止,求ω1的值;
解析 当水平转盘以角速度ω1匀速转动时,物块与转盘刚好能相对静止,则此时物块所需向心力恰好完全由最大静摩擦力提供,则μmg=mrω12
(2)如图乙,将物块和转轴用细绳相连,当转盘的角速度ω2= 时,求细绳的拉
力FT2的大小;
答案 0
解析 由于ω2<ω1,物块受到的最大静摩擦力大于所需向心力,此时绳对物块没有拉力,故FT2=0.
(3)将物块和转轴用细绳相连,当转盘的角速度ω3= 时,求细绳的拉力FT3的大小.
解析 由于ω3>ω1,物块受到的最大静摩擦力不足以提供所需的向心力,此时绳对物块有拉力,则μmg+FT3=mω32r,可得此时绳子对物块拉力的大小为FT3= μmg.
1.(轻绳模型)杂技演员表演“水流星”,在长为1.6 m的细绳的一端,系一个与水的总质量为m=0.5 kg的大小不计的盛水容器,以绳的另一端为圆心,在竖直平面内做圆周运动,如图7所示,若“水流星”通过最高点时的速率为4 m/s,则下列说法正确的是(g取10 m/s2)
A.“水流星”通过最高点时,有水从容器中流出
B.“水流星”通过最高点时,绳的张力及容器底部受到的压力均为零
C.“水流星”通过最高点时,处于完全失重状态,不受力的作用
D.“水流星”通过最高点时,绳子的拉力大小为5 N
1
2
3
4
图7
√
解析 “水流星”在最高点的临界速度v= =4 m/s,由此知绳的拉力恰好为零,且水恰好不流出,故选B.
2.(过山车模型)(多选)如图8所示,质量为m的小球在竖直平面内的光滑圆环内侧做圆周运动.圆环半径为R,小球半径不计,小球经过圆环内侧最高点时刚好不脱离圆环,则其通过最高点时下列表述正确的是
A.小球对圆环的压力大小等于mg
B.重力mg充当小球做圆周运动所需的向心力
C.小球的线速度大小等于
D.小球的向心加速度大小等于g
1
2
3
4
√
√
图8
√
1
2
3
4
解析 因为小球经过圆环内侧最高点时刚好不脱离圆环,故在最高点时小球对圆环的压力为零,选项A错误;
1
2
3
4
图9
√
1
2
3
4
4.(圆周运动的临界问题)如图10所示,A、B、C三个物体放在旋转的水平圆盘面上,物体与盘面间的最大静摩擦力均是其重力的k倍,三物体的质量分别为2m、m、m,它们离转轴的距离分别为R、R、2R.当圆盘旋转时,若A、B、C三物体均相对圆盘静止,则下列说法正确的是
A.A的向心加速度最大
B.B和C所受摩擦力大小相等
C.当圆盘转速缓慢增大时,C比A先滑动
D.当圆盘转速缓慢增大时,B比A先滑动
1
2
3
4
图10
√
