苏科版初中数学九年级下册 7.1 正切 教案
文档属性
| 名称 | 苏科版初中数学九年级下册 7.1 正切 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 186.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 00:00:00 | ||
图片预览

文档简介
7.1 正切
教学目标:
1 经历利用相似的直角三角形探索直角三角形边角关系的过程,理解正切的概念并能进行简单的计算;
2 在观察、探索、比较等数学活动中,感受函数和数形结合的数学思想,培养学生的符号意识,发展合情推理能力,发展学生理性的数学思维;
3 获得分析问题和解决问题的一些基本方法,发展创新意识;
4 体会数学的特点,了解数学的价值,养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯,形成实事求是的科学态度。
教学重点和难点:
重点:正切的定义
难点:计算一个锐角的正切值的方法
教学方法:自主探究、讨论归纳
教学过程:
一、设疑自探
显示几幅黄山图片,让学生感受走哪段更费力?哪段山路更陡
解疑合探
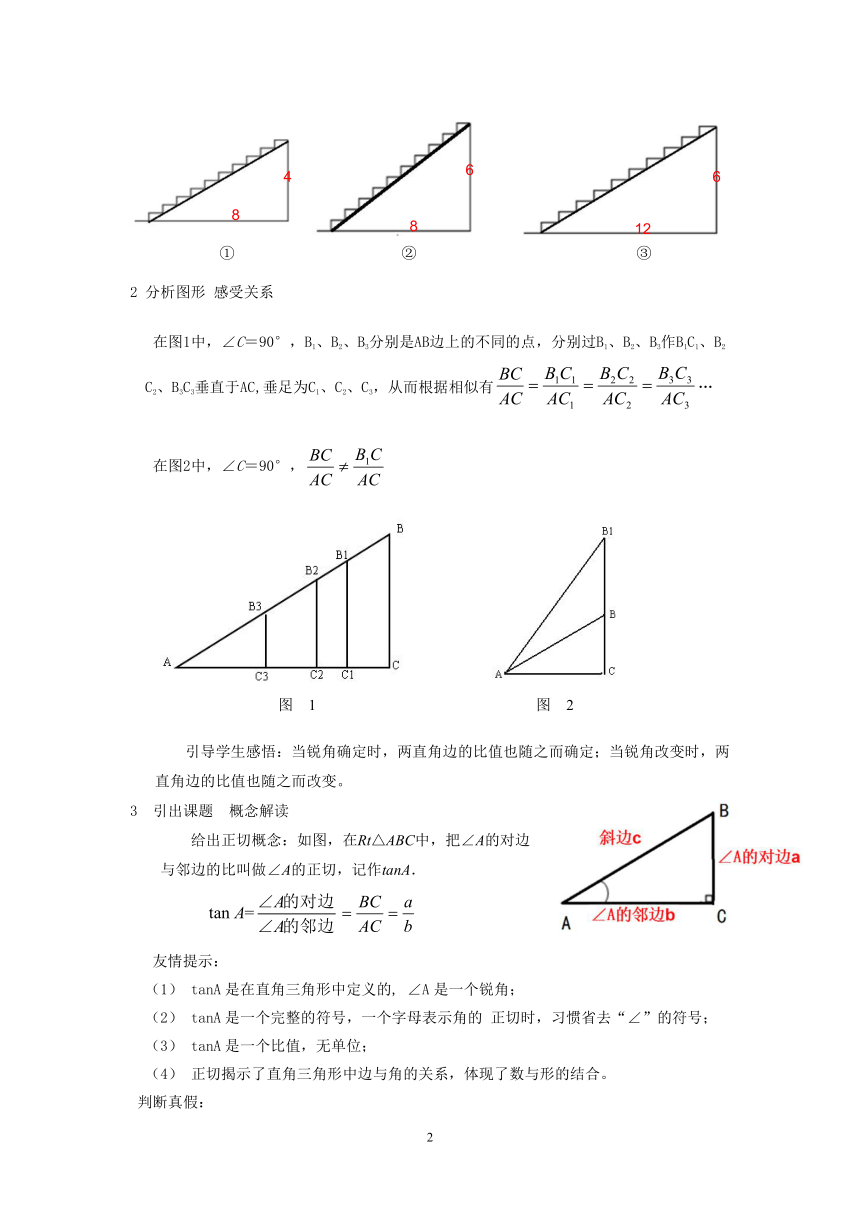
1 观察图形 判断比较
引导学生观察比较②、③哪个台阶更陡?你是如何判断的?
引导学生观察比较①、②哪个台阶更陡?你是如何判断的?
引导学生观察比较①、③哪个台阶更陡?你是如何判断的?
(
①
②
③
) (
12
) (
8
8
6
6
4
)
2 分析图形 感受关系
在图1中,∠C=90°,B1、B2、B3分别是AB边上的不同的点,分别过B1、B2、B3作B1C1、B2C2、B3C3垂直于AC,垂足为C1、C2、C3,从而根据相似有…
在图2中,∠C=90°,
(
图
1
图
2
)
引导学生感悟:当锐角确定时,两直角边的比值也随之而确定;当锐角改变时,两直角边的比值也随之而改变。
3 引出课题 概念解读
给出正切概念:如图,在Rt△ABC中,把∠A的对边
与邻边的比叫做∠A的正切,记作tanA.
友情提示:
(1) tanA是在直角三角形中定义的, ∠A是一个锐角;
(2) tanA是一个完整的符号,一个字母表示角的 正切时,习惯省去“∠”的符号;
(3) tanA是一个比值,无单位;
(4) 正切揭示了直角三角形中边与角的关系,体现了数与形的结合。
判断真假:
(1)如图 (1), ( )
(2)如图 (2), ( )
(3)如图 (2), ( )
(
D
)三 质疑共探
1 例题示范 引申变式
例 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10
让学生思考:根据已知条件,利用所学知识,你能求出哪些量?
变式1:
在Rt△ABC中,∠C=90°,AB=10,tanA=,利用所学知识,你能求出哪些量?
学生尝试作变式并求解
变式2:
作斜边AB边上的高CD,垂足为D,你能求出∠ACD的正切值吗?
并让学生通过计算、观察并比较发现结论:
(1) 等角的正切值相等; (2)互余的角的正切值互为倒数。
2 触类旁通 自主练习
(1)在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
(
图
①
图
②
) A.扩大100倍 B.缩小100倍 C.不变 D.不能确定
(2)如图①,在Rt△ABC中,AB=AC
如图②,等边三角形ABC中,AB=AC=BC
你能用今天所学的知识求出哪些角的正切值?
通过计算、观察并比较发现结论,接上面已有的结论(1)、(2),有 :
(3) tan30°= tan45°=1 tan60°=
(4) 锐角的正切值随着锐角的增大而增大
(并由课堂识初的左图来作说明)
四 悬疑再探
1 对于本节的学习,你学到什么知识?掌握了什么方法?体会了哪些思想?积累了哪些经验?谁还有什么问或者不明白的地方?
2材料阅读:
“三角学”一词,是由希腊文三角形与测量二字构成的, 16世纪,德国数学家雷提库斯把锐角三角函数定义为直角三角形的边长之比,并采用了六个函数(正切、正弦、余弦、余切、正割、余割)。三角函数在建筑,航海及天文等方面测量、计算中有着重要的作用.
三角测量在我国出现的很早.据记载,早在公元前两千年,大禹就利用三角形的边角正切函数关系,来对山川地势进行测量并作计算.
3 你能沿着本节探究学习正切函数的基本思路和经验,去尝试发现直角三角形的边角关系的其它类型的三角函数吗?
1
教学目标:
1 经历利用相似的直角三角形探索直角三角形边角关系的过程,理解正切的概念并能进行简单的计算;
2 在观察、探索、比较等数学活动中,感受函数和数形结合的数学思想,培养学生的符号意识,发展合情推理能力,发展学生理性的数学思维;
3 获得分析问题和解决问题的一些基本方法,发展创新意识;
4 体会数学的特点,了解数学的价值,养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯,形成实事求是的科学态度。
教学重点和难点:
重点:正切的定义
难点:计算一个锐角的正切值的方法
教学方法:自主探究、讨论归纳
教学过程:
一、设疑自探
显示几幅黄山图片,让学生感受走哪段更费力?哪段山路更陡
解疑合探
1 观察图形 判断比较
引导学生观察比较②、③哪个台阶更陡?你是如何判断的?
引导学生观察比较①、②哪个台阶更陡?你是如何判断的?
引导学生观察比较①、③哪个台阶更陡?你是如何判断的?
(
①
②
③
) (
12
) (
8
8
6
6
4
)
2 分析图形 感受关系
在图1中,∠C=90°,B1、B2、B3分别是AB边上的不同的点,分别过B1、B2、B3作B1C1、B2C2、B3C3垂直于AC,垂足为C1、C2、C3,从而根据相似有…
在图2中,∠C=90°,
(
图
1
图
2
)
引导学生感悟:当锐角确定时,两直角边的比值也随之而确定;当锐角改变时,两直角边的比值也随之而改变。
3 引出课题 概念解读
给出正切概念:如图,在Rt△ABC中,把∠A的对边
与邻边的比叫做∠A的正切,记作tanA.
友情提示:
(1) tanA是在直角三角形中定义的, ∠A是一个锐角;
(2) tanA是一个完整的符号,一个字母表示角的 正切时,习惯省去“∠”的符号;
(3) tanA是一个比值,无单位;
(4) 正切揭示了直角三角形中边与角的关系,体现了数与形的结合。
判断真假:
(1)如图 (1), ( )
(2)如图 (2), ( )
(3)如图 (2), ( )
(
D
)三 质疑共探
1 例题示范 引申变式
例 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10
让学生思考:根据已知条件,利用所学知识,你能求出哪些量?
变式1:
在Rt△ABC中,∠C=90°,AB=10,tanA=,利用所学知识,你能求出哪些量?
学生尝试作变式并求解
变式2:
作斜边AB边上的高CD,垂足为D,你能求出∠ACD的正切值吗?
并让学生通过计算、观察并比较发现结论:
(1) 等角的正切值相等; (2)互余的角的正切值互为倒数。
2 触类旁通 自主练习
(1)在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
(
图
①
图
②
) A.扩大100倍 B.缩小100倍 C.不变 D.不能确定
(2)如图①,在Rt△ABC中,AB=AC
如图②,等边三角形ABC中,AB=AC=BC
你能用今天所学的知识求出哪些角的正切值?
通过计算、观察并比较发现结论,接上面已有的结论(1)、(2),有 :
(3) tan30°= tan45°=1 tan60°=
(4) 锐角的正切值随着锐角的增大而增大
(并由课堂识初的左图来作说明)
四 悬疑再探
1 对于本节的学习,你学到什么知识?掌握了什么方法?体会了哪些思想?积累了哪些经验?谁还有什么问或者不明白的地方?
2材料阅读:
“三角学”一词,是由希腊文三角形与测量二字构成的, 16世纪,德国数学家雷提库斯把锐角三角函数定义为直角三角形的边长之比,并采用了六个函数(正切、正弦、余弦、余切、正割、余割)。三角函数在建筑,航海及天文等方面测量、计算中有着重要的作用.
三角测量在我国出现的很早.据记载,早在公元前两千年,大禹就利用三角形的边角正切函数关系,来对山川地势进行测量并作计算.
3 你能沿着本节探究学习正切函数的基本思路和经验,去尝试发现直角三角形的边角关系的其它类型的三角函数吗?
1
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
